spectrogram
短時間フーリエ変換を使用したスペクトログラム
構文
説明
また、[___, は ps] = spectrogram(___,spectrumtype)x のスペクトログラムに比例する行列 ps も返します。
spectrumtypeを"psd"として指定すると、psの各列には、ウィンドウが適用されたセグメントのパワー スペクトル密度 (PSD) の推定が格納されます。spectrumtypeを"power"として指定すると、psの各列には、ウィンドウが適用されたセグメントのパワー スペクトルの推定が格納されます。
[___] = spectrogram(___,"reassigned") は、各 PSD またはパワー スペクトル推定を、そのエネルギーの中心の位置に再代入します。十分に局所化された時相成分またはスペクトル成分が信号に含まれる場合、このオプションは、よりシャープなスペクトログラムを生成します。
[___] = spectrogram(___, は、freqrange)freqrange で指定した周波数範囲での PSD またはパワー スペクトル推定を返します。freqrange の有効なオプションは、"onesided"、"twosided" および "centered" です。
[___] = spectrogram(___, は、名前と値の引数を使用して追加オプションを指定します。オプションには、最小しきい値と出力時間次元が含まれます。Name=Value)
例
正弦波の和から構成される信号のサンプルを 個生成します。正弦波の正規化周波数は、 ラジアン/サンプルおよび ラジアン/サンプルです。高周波数の正弦波の振幅は、他の正弦波の振幅の 10 倍です。
N = 1024; n = 0:N-1; w0 = 2*pi/5; x = sin(w0*n)+10*sin(2*w0*n);
関数の既定の設定を使用して、短時間フーリエ変換を計算します。スペクトログラムをプロットします。
s = spectrogram(x);
spectrogram(x,'yaxis')
計算を繰り返します。
長さ のセクションに信号を分割します。
ハミング ウィンドウを使用して、セクションにウィンドウを適用します。
隣接するセクション間で 50% のオーバーラップを指定します。
FFT を計算するには、 点を使用します。ここで、 です。
2 つの方法の結果が同じになることを確認します。
Nx = length(x); nsc = floor(Nx/4.5); nov = floor(nsc/2); nff = max(256,2^nextpow2(nsc)); t = spectrogram(x,hamming(nsc),nov,nff); maxerr = max(abs(abs(t(:))-abs(s(:))))
maxerr = 0
長さが等しく、セクション間のオーバーラップが 50% である 8 つのセクションに信号を分割します。前のステップと同じ FFT 長を指定します。短時間フーリエ変換を計算し、前の 2 つの手順と結果が同じであることを確認します。
ns = 8; ov = 0.5; lsc = floor(Nx/(ns-(ns-1)*ov)); t = spectrogram(x,lsc,floor(ov*lsc),nff); maxerr = max(abs(abs(t(:))-abs(s(:))))
maxerr = 0
600 Hz で 2 秒間サンプリングされた複素数値凸 2 次チャープで構成される信号を生成します。チャープの初期周波数は 250 Hz、最終周波数は 50 Hz です。
fs = 6e2; ts = 0:1/fs:2; x = chirp(ts,250,ts(end),50,"quadratic",0,"convex","complex");
関数 spectrogram
関数 spectrogram を使用して信号の STFT を計算します。
信号を、それぞれ サンプルの長さのセグメントに分割します。
隣接するセグメント間に 個のサンプルのオーバーラップを指定します。
最後の短いセグメントを破棄します。
各セグメントにバートレット ウィンドウを適用します。
点で各セグメントの離散フーリエ変換を評価します。既定では、複素数値信号の場合、
spectrogramは両側変換を計算します。
M = 49; L = 11; g = bartlett(M); Ndft = 1024; [s,f,t] = spectrogram(x,g,L,Ndft,fs);
関数 waterplot を使用して、STFT の振幅の 2 乗として定義されるスペクトログラムを計算し、表示します。
waterplot(s,f,t)

STFT の定義
定義を使用して サンプルの信号の STFT を計算します。信号を 個のオーバーラップ セグメントに分割します。各セグメントにウィンドウを適用し、それぞれについて、 点での離散フーリエ変換を評価します。
segs = framesig(1:length(x),M,OverlapLength=L); X = fft(x(segs).*g,Ndft);
STFT の時間範囲と周波数範囲を計算します。
時間値を求めるには、時間ベクトルをオーバーラップ セグメントに分割します。時間値は、下端でオープンの区間として扱われる各セグメントの中間点です。
周波数値を求めるには、ゼロ周波数でクローズ、下端でオープンとなるナイキスト区間を指定します。
framedT = ts(segs); tint = mean(framedT(2:end,:)); fint = 0:fs/Ndft:fs-fs/Ndft;
spectrogram の出力を定義と比較します。スペクトログラムを表示します。
maxdiff = max(max(abs(s-X)))
maxdiff = 0
waterplot(X,fint,tint)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
1.4 kHz で 2 秒間サンプリングされたチャープで構成される信号を生成します。チャープの周波数は、測定時間中に 600 Hz から 100 Hz に線形的に減少します。
fs = 1400; x = chirp(0:1/fs:2,600,2,100);
stft 既定
関数 spectrogram と stft を使用して信号の STFT を計算します。関数 stft の既定の値を使用します。
信号を 128 サンプルのセグメントに分割し、各セグメントに周期的ハン ウィンドウを適用します。
隣接するセグメント間に 96 個のサンプルのオーバーラップを指定します。この長さはウィンドウの長さの 75% と等価です。
128 の DFT 点を指定し、STFT の中央を周波数ゼロに揃え、周波数は Hz 単位で表します。
2 つの結果が等価であることを確認します。
M = 128; g = hann(M,"periodic"); L = 0.75*M; Ndft = 128; [sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered"); [s,f,t] = stft(x,fs); dff = max(max(abs(sp-s)))
dff = 0
関数 mesh を使用して、2 つの出力をプロットします。
nexttile mesh(tp,fp,abs(sp).^2) title("spectrogram") view(2), axis tight nexttile mesh(t,f,abs(s).^2) title("stft") view(2), axis tight

spectrogram 既定
関数 spectrogram の既定の値を使用して計算を繰り返します。
信号を の長さのセグメントに分割します。ここで、 は信号の長さです。各セグメントにハミング ウィンドウを適用します。
セグメント間で 50% のオーバーラップを指定します。
FFT を計算するには、 点を使用します。正の正規化周波数のみ、スペクトログラムを計算します。
M = floor(length(x)/4.5); g = hamming(M); L = floor(M/2); Ndft = max(256,2^nextpow2(M)); [sx,fx,tx] = spectrogram(x); [st,ft,tt] = stft(x,Window=g,OverlapLength=L, ... FFTLength=Ndft,FrequencyRange="onesided"); dff = max(max(sx-st))
dff = 0
関数 waterplot を使用して、2 つの出力をプロットします。どちらの場合も、周波数軸を で除算します。stft 出力の場合、サンプル数を有効なサンプル レート で除算します。
figure nexttile waterplot(sx,fx/pi,tx) title("spectrogram") nexttile waterplot(st,ft/pi,tt/(2*pi)) title("stft")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency/\pi") ylabel("Samples") end
関数 spectrogram を使用して信号の瞬時周波数を測定し、追跡します。
1 kHz で 2 秒間サンプリングされた 2 次チャープを生成します。初期周波数が 100 Hz で、1 秒後には 200 Hz に増加するようにチャープを指定します。
fs = 1000;
t = 0:1/fs:2-1/fs;
y = chirp(t,100,1,200,'quadratic');関数 spectrogram に実装された短時間フーリエ変換を使用して、チャープのスペクトルを推定します。信号にハミング ウィンドウを適用し、長さ 100 のセクションに分割します。隣り合ったセクション間のオーバーラップのサンプル 80 個を指定し、周波数 におけるスペクトルを評価します。
spectrogram(y,100,80,100,fs,'yaxis')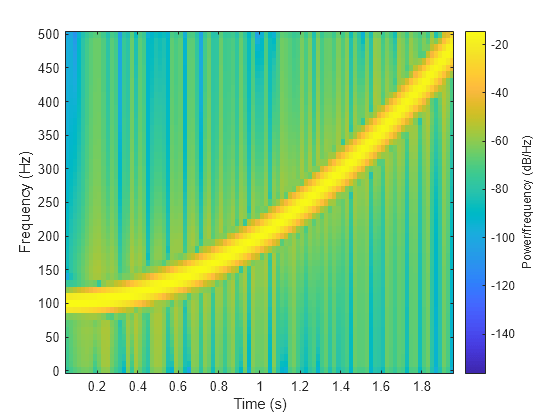
の時間点にわたる最大エネルギーをもつ時間-周波数リッジを検出することにより、チャープの周波数を追跡します。スペクトログラム プロットに瞬時周波数を重ね合わせます。
[~,f,t,p] = spectrogram(y,100,80,100,fs); [fridge,~,lr] = tfridge(p,f); hold on plot3(t,fridge,abs(p(lr)),'LineWidth',4) hold off

正弦関数的に変化する周波数成分をもつチャープのサンプルを 512 個生成します。
N = 512; n = 0:N-1; x = exp(1j*pi*sin(8*n/N)*32);
チャープの中央揃えの短時間フーリエ変換を計算します。信号を 16 サンプルがオーバーラップする 32 サンプルのセグメントに分割します。64 個の DFT ポイントを指定します。スペクトログラムをプロットします。
[scalar,fs,ts] = spectrogram(x,32,16,64,'centered'); spectrogram(x,32,16,64,'centered','yaxis')

区間 に対して 64 等間隔周波数のスペクトログラムを計算すると、同じ結果が得られます。'centered' オプションは必要ありません。
fintv = -pi+pi/32:pi/32:pi;
[vector,fv,tv] = spectrogram(x,32,16,fintv);
spectrogram(x,32,16,fintv,'yaxis')
電圧制御発振器と 3 つのガウス原子で構成される信号を生成します。信号は kHz で 2 秒間サンプリングされます。
fs = 2000; tx = 0:1/fs:2; gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.03^2)).*sin(2*pi*f.*x)*A'; s = gaussFun([1 1 1],tx',[0.1 0.65 1],[2 6 2]*100)*1.5; x = vco(chirp(tx+.1,0,tx(end),3).*exp(-2*(tx-1).^2),[0.1 0.4]*fs,fs); x = s+x';
短時間フーリエ変換
関数 pspectrum を使用して STFT を計算します。
サンプル信号を、 ミリ秒の時間分解能に対応する長さ のサンプルのセグメントに分割します。
個のサンプル、または隣接するセグメント間の 20% のオーバーラップを指定します。
カイザー ウィンドウを使用して各セグメントにウィンドウを適用し、漏れには を指定します。
M = 80; L = 16; lk = 0.7; [S,F,T] = pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk);
関数 spectrogram で得られた結果と比較します。
ウィンドウの長さとオーバーラップをサンプル単位で直接指定します。
pspectrumは常にカイザー ウィンドウを として使用します。漏れ とウィンドウの形状係数 は、 の関係にあります。pspectrumは、離散フーリエ変換の計算に常に 個の点を使用します。両側または中央揃えの周波数範囲の変換を計算したい場合にこの数値を指定することができます。一方、実信号の既定値である片側変換の場合、spectrogramは 個の点を使用します。あるいは、この例にあるように、変換を計算したい周波数のベクトルを指定することができます。信号を 個のセグメントに厳密に分割できない場合、
spectrogramは信号を切り捨て、pspectrumは信号をゼロでパディングして追加のセグメントを作成します。出力を等価にするには、最後のセグメントと時間ベクトルの最後の要素を削除します。spectrogramは、振幅の 2 乗をスペクトログラムとする STFT を返します。pspectrumは、あらかじめ係数 で除算してから 2 乗した各セグメントのパワー スペクトルを返します。片側変換の場合、
pspectrumはスペクトログラムに追加の係数 2 を追加します。
g = kaiser(M,40*(1-lk)); k = (length(x)-L)/(M-L); if k~=floor(k) S = S(:,1:floor(k)); T = T(1:floor(k)); end [s,f,t] = spectrogram(x/sum(g)*sqrt(2),g,L,F,fs);
関数 waterplot を使用して、これら 2 つの関数によって計算されたスペクトログラムを表示します。
subplot(2,1,1) waterplot(sqrt(S),F,T) title("pspectrum") subplot(2,1,2) waterplot(s,f,t) title("spectrogram")

maxd = max(max(abs(abs(s).^2-S)))
maxd = 2.4419e-08
パワー スペクトルと簡易プロット
関数 spectrogram は、各セグメントのパワー スペクトルまたはパワー スペクトル密度に対応する 4 番目の引数をもちます。pspectrum の出力と同様、ps 引数はあらかじめ 2 乗されており、正規化係数 を含みます。実信号の片側スペクトログラムの場合も、追加の係数 2 を含める必要があります。関数のスケーリング引数を "power" に設定します。
[~,~,~,ps] = spectrogram(x*sqrt(2),g,L,F,fs,"power");
max(abs(S(:)-ps(:)))ans = 2.4419e-08
pspectrum と spectrogram は、出力引数なしで呼び出された場合に、信号のスペクトログラムをデシベル単位でプロットします。片側スペクトログラムの場合は係数 2 を含めます。両方のプロットで同じになるようにカラーマップを設定します。x の範囲を同じ値に設定して、pspectrum プロットの最後にある追加のセグメントが表示されるようにします。spectrogram プロットの y 軸に周波数を表示します。
subplot(2,1,1) pspectrum(x,fs,"spectrogram", ... TimeResolution=M/fs,OverlapPercent=L/M*100, ... Leakage=lk) title("pspectrum") cc = clim; xl = xlim; subplot(2,1,2) spectrogram(x*sqrt(2),g,L,F,fs,"power","yaxis") title("spectrogram") clim(cc) xlim(xl)

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
1 kHz で 2 秒間サンプリングされたチャープ信号を生成します。初期周波数が 100 Hz で、1 秒後には 200 Hz に増加するようにチャープを指定します。
fs = 1000;
t = 0:1/fs:2;
y = chirp(t,100,1,200,"quadratic");再割り当てされた信号のスペクトログラムを推定します。
信号に形状パラメーター のカイザー ウィンドウを適用し、長さ 128 のセクションに分割します。
隣り合ったセクション間のオーバーラップのサンプルを 120 個に指定します。
周波数および 時間ビンでスペクトルを評価します。
出力引数なしで関数 spectrogram を使用して、再割り当てされたスペクトログラムをプロットします。y 軸に周波数、x 軸に時間を表示します。
spectrogram(y,kaiser(128,18),120,128,fs, ... "reassigned","yaxis")

関数 imagesc を使用してプロットをやり直します。周波数値が下から上に増加するように、y 軸の方向を指定します。デシベル変換時に負の無限大となることを避けるため、再割り当てされたスペクトログラムに eps を追加します。
[~,fr,tr,pxx] = spectrogram(y,kaiser(128,18),120,128,fs, ... "reassigned"); imagesc(tr,fr,pow2db(pxx+eps)) axis xy xlabel("Time (s)") ylabel("Frequency (Hz)") colorbar

1 kHz で 2 秒間サンプリングされたチャープ信号を生成します。初期周波数が 100 Hz で、1 秒後には 200 Hz に増加するようにチャープを指定します。
Fs = 1000;
t = 0:1/Fs:2;
y = chirp(t,100,1,200,'quadratic');信号の時間依存のパワー スペクトル密度 (PSD) を推定します。
信号に形状パラメーター のカイザー ウィンドウを適用し、長さ 128 のセクションに分割します。
隣り合ったセクション間のオーバーラップのサンプルを 120 個に指定します。
周波数および 時間ビンでスペクトルを評価します。
各 PSD 推定の重心の周波数および時間を出力します。 dB より小さい PSD の要素をゼロに設定します。
[~,~,~,pxx,fc,tc] = spectrogram(y,kaiser(128,18),120,128,Fs, ... 'MinThreshold',-30);
重心の周波数および時間の関数として非ゼロの要素をプロットします。
plot(tc(pxx>0),fc(pxx>0),'.')
2 kHz で 2 秒間サンプリングされた実数値のチャープで構成される信号を生成します。
fs = 2000;
tx = 0:1/fs:2;
x = vco(-chirp(tx,0,tx(end),2).*exp(-3*(tx-1).^2), ...
[0.1 0.4]*fs,fs).*hann(length(tx))';両側スペクトログラム
信号の両側 STFT を計算してプロットします。
信号を、それぞれ サンプルの長さのセグメントに分割します。
隣接するセグメント間に 個のサンプルのオーバーラップを指定します。
最後の短いセグメントを破棄します。
各セグメントにフラットトップ ウィンドウを適用します。
点で各セグメントの離散フーリエ変換を評価します。このとき、点の数が奇数であることに注意します。
M = 73;
L = 24;
g = flattopwin(M);
Ndft = 895;
neven = ~mod(Ndft,2);
[stwo,f,t] = spectrogram(x,g,L,Ndft,fs,"twosided");出力引数なしで関数 spectrogram を使用し、両側スペクトログラムをプロットします。
spectrogram(x,g,L,Ndft,fs,"twosided","power","yaxis")

定義を使用して両側スペクトログラムを計算します。隣接するセグメント間で サンプルがオーバーラップする サンプルのセグメントに信号を分割します。各セグメントにウィンドウを適用し、それぞれについて、 点での離散フーリエ変換を計算します。
y = framesig(x,M,Window=g,OverlapLength=L); Xtwo = fft(y,Ndft);
時間範囲と周波数範囲を計算します。
時間値を求めるには、時間ベクトルをオーバーラップ セグメントに分割します。時間値は、下端でオープンの区間として扱われる各セグメントの中間点です。
周波数値を求めるには、ゼロ周波数でクローズ、上端でオープンとなるナイキスト区間を指定します。
framedT = framesig(tx,M,OverlapLength=L); ttwo = mean(framedT(2:end,:)); ftwo = 0:fs/Ndft:fs*(1-1/Ndft);
spectrogram の出力を定義と比較します。関数 waterplot を使用して、スペクトログラムを表示します。
diffs = [max(max(abs(stwo-Xtwo)));
max(abs(f-ftwo'));
max(abs(t-ttwo))]diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xtwo,ftwo,ttwo) title("Two-Sided, Definition") nexttile waterplot(stwo,f,t) title("Two-Sided, spectrogram Function")

中央揃えのスペクトログラム
信号の中央揃えのスペクトログラムを計算します。
両側 STFT で使用したのと同じ時間値を使用します。
関数
fftshiftを使用して、STFT のゼロ周波数成分をスペクトルの中央にシフトします。が奇数の場合、周波数範囲は両側でオープンとなります。 が偶数の場合、周波数範囲は下端でオープン、上端でクローズとなります。
出力を比較してスペクトログラムを表示します。
tcen = ttwo; if ~neven Xcen = fftshift(Xtwo,1); fcen = -fs/2*(1-1/Ndft):fs/Ndft:fs/2; else Xcen = fftshift(circshift(Xtwo,-1),1); fcen = (-fs/2*(1-1/Ndft):fs/Ndft:fs/2)+fs/Ndft/2; end [scen,f,t] = spectrogram(x,g,L,Ndft,fs,"centered"); diffs = [max(max(abs(scen-Xcen))); max(abs(f-fcen')); max(abs(t-tcen))]
diffs = 3×1
10-12 ×
0
0.2274
0.0002
figure nexttile waterplot(Xcen,fcen,tcen) title("Centered, Definition") nexttile waterplot(scen,f,t) title("Centered, spectrogram Function")

片側スペクトログラム
信号の片側スペクトログラムを計算します。
両側 STFT で使用したのと同じ時間値を使用します。
が奇数の場合、片側 STFT は両側 STFT の最初の 行により構成されます。 が偶数の場合、片側 STFT は両側 STFT の最初の 行により構成されます。
が奇数の場合、周波数範囲はゼロ周波数でクローズ、ナイキスト周波数でオープンとなります。 が偶数の場合、周波数範囲は両側でクローズとなります。
出力を比較してスペクトログラムを表示します。実数値信号の場合、"onesided" 引数はオプションです。
tone = ttwo; if ~neven Xone = Xtwo(1:(Ndft+1)/2,:); else Xone = Xtwo(1:Ndft/2+1,:); end fone = 0:fs/Ndft:fs/2; [sone,f,t] = spectrogram(x,g,L,Ndft,fs); diffs = [max(max(abs(sone-Xone))); max(abs(f-fone')); max(abs(t-tone))]
diffs = 3×1
10-12 ×
0
0.1137
0.0002
figure nexttile waterplot(Xone,fone,tone) title("One-Sided, Definition") nexttile waterplot(sone,f,t) title("One-Sided, spectrogram Function")

function waterplot(s,f,t) % Waterfall plot of spectrogram waterfall(f,t,abs(s)'.^2) set(gca,XDir="reverse",View=[30 50]) xlabel("Frequency (Hz)") ylabel("Time (s)") end
関数 spectrogram は、4 番目の出力引数として、各セグメントのパワー スペクトル密度 (PSD) またはパワー スペクトルのいずれかを含む行列をもちます。パワー スペクトルは、PSD にウィンドウの等価ノイズ帯域幅 (ENBW) を乗算した値と等価です。
1 kHz で 1 秒間サンプリングされた対数チャープで構成される信号を生成します。チャープの初期周波数は 400 Hz で、測定の最後には 10 Hz に減少します。
fs = 1000;
tt = 0:1/fs:1-1/fs;
y = chirp(tt,400,tt(end),10,"logarithmic");サンプル レートによる PSD とパワー スペクトルのセグメント化
信号を 102 サンプルのセグメントに分割し、各セグメントにハン ウィンドウを適用します。隣り合ったセグメント間のオーバーラップを 12 サンプル、DFT 点を 1024 に指定します。
M = 102; g = hann(M); L = 12; Ndft = 1024;
既定の PSD スペクトル タイプで信号のスペクトログラムを計算します。STFT、およびセグメントのパワー スペクトル密度の配列を出力します。
[s,f,t,p] = spectrogram(y,g,L,Ndft,fs);
スペクトル タイプを "power" に指定して計算を繰り返します。STFT、およびセグメントのパワー スペクトルの配列を出力します。
[r,~,~,q] = spectrogram(y,g,L,Ndft,fs,"power");どちらの場合もスペクトログラムが同じになることを確認します。周波数に対数スケールを使用して、スペクトログラムをプロットします。
max(max(abs(s).^2-abs(r).^2))
ans = 0
waterfall(f,t,abs(s)'.^2) set(gca,XScale="log",... XDir="reverse",View=[30 50])

パワー スペクトルが、パワー スペクトル密度にウィンドウの ENBW を乗算した値と等価であることを確認します。
max(max(abs(q-p*enbw(g,fs))))
ans = 1.1102e-16
セグメントのパワー スペクトルの行列が、スペクトログラムに比例していることを確認します。比例係数は、ウィンドウ要素の和の 2 乗です。
max(max(abs(s).^2-q*sum(g)^2))
ans = 0
正規化周波数による PSD とパワー スペクトルのセグメント化
計算を繰り返しますが、今度は正規化周波数で計算します。サンプル レートを として指定した場合、結果は同じになります。
[~,~,~,pn] = spectrogram(y,g,L,Ndft);
[~,~,~,qn] = spectrogram(y,g,L,Ndft,"power");
max(max(abs(qn-pn*enbw(g,2*pi))))ans = 1.1102e-16
減少する 2 つのチャープと広帯域のスプラッター音を含むオーディオ信号を読み込みます。短時間フーリエ変換を計算します。波形を 300 サンプルがオーバーラップする 400 サンプルのセグメントに分割します。スペクトログラムをプロットします。
load splat % To hear, type soundsc(y,Fs) sg = 400; ov = 300; spectrogram(y,sg,ov,[],Fs,"yaxis") colormap bone

関数 spectrogram を使用し、信号のパワー スペクトル密度 (PSD) を出力します。
[s,f,t,p] = spectrogram(y,sg,ov,[],Fs);
関数 medfreq を使用して 2 つのチャープを追跡します。より強い低周波のチャープを検出するには、探索を 100 Hz より高い周波数と広帯域音が始まる前の時間に制限します。
f1 = f > 100; t1 = t < 0.75; m1 = medfreq(p(f1,t1),f(f1));
微弱な高周波のチャープを検出するには、探索を 2500 Hz より高い周波数と 0.3 秒 ~ 0.65 秒の時間に制限します。
f2 = f > 2500; t2 = t > 0.3 & t < 0.65; m2 = medfreq(p(f2,t2),f(f2));
結果をスペクトログラムに重ね合わせます。kHz の単位で表すために周波数の値を 1000 で除算します。
hold on plot(t(t1),m1/1000,LineWidth=4) plot(t(t2),m2/1000,LineWidth=4) hold off

10 kHz でサンプリングされた 2 秒間の信号を生成します。信号の瞬時周波数を時間の三角形関数として指定します。
fs = 10e3; t = 0:1/fs:2; x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*fs,fs);
信号のスペクトログラムを計算してプロットします。長さ 256 で形状パラメーター のカイザー ウィンドウを使用します。セクション間のオーバーラップのサンプル 220 個と DFT 点 512 個を指定します。周波数を y 軸にプロットします。既定のカラーマップとビューを使用します。
spectrogram(x1,kaiser(256,5),220,512,fs,'yaxis')
スペクトログラムをウォーターフォール プロットとして表示するようにビューを変更します。カラーマップを bone に設定します。
view(-45,65)
colormap bone
R2025a 以降
axes ハンドルとパネル コンテナーに 4 つの信号のスペクトログラムをプロットします。spectrogram を出力引数なしで使用すると、関数はパワー スペクトル密度 (PSD) 推定を含む便利なプロットを返します。特定の axes ハンドルまたはパネル コンテナーでこのプロットを再現するには、ターゲットの Parent 入力引数を使用して spectrogram を指定します。
4 つの振動信号 (サンプル レート 10 kHz、3 秒間) を作成します。
x1:ノコギリ波形状の振動信号x2:指数関数的に減衰する振動信号x3:複素正弦波エンベロープx4:2 次スイープ チャープ
Fs = 10e3; t = 0:1/Fs:3; x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*Fs,Fs); x2 = vco(sin(2*pi*t).*exp(-t),[0.1 0.4]*Fs,Fs) ... + 0.01*sin(2*pi*0.25*Fs*t); x3 = exp(1j*pi*sin(4*t)*Fs/10); x4 = chirp(t,Fs/10,t(end),Fs/2.5,"quadratic");
信号スペクトログラムを計算するための仕様を、次のように定義します。512 個の DFT 点、256 サンプルのカイザー ウィンドウ、および 220 サンプルのオーバーラップ長。
nfft = 512; g = kaiser(256,5); ol = 220;
Axes ハンドルへのスペクトログラムのプロット
新しい Figure ウィンドウの南西隅と北東隅に 2 つの axes ハンドルを作成します。
fig = figure; ax1 = axes(fig,Position=[0.05 0.1 0.55 0.45]); ax2 = axes(fig,Position=[0.55 0.7 0.42 0.28]);
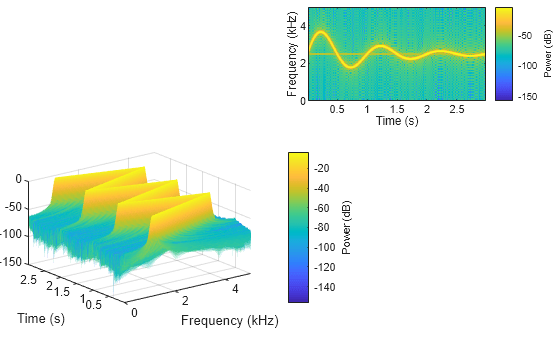
信号 x1 と x2 のパワー スペクトルを Figure の南西軸と北東軸にそれぞれプロットします。本来の 3-D の視線で x1 のスペクトログラムを表示します。x2 のスペクトログラムの y 軸に周波数を表示します。
spectrogram(x1,g,ol,nfft,Fs,"power",Parent=ax1); view(ax1,3); spectrogram(x2,g,ol,nfft,Fs,"power","yaxis",Parent=ax2);
UI ベースの Axes ハンドルへのスペクトログラムのプロット
新しい UI Figure ウィンドウの北西隅に axes ハンドルを作成します。
uif = uifigure(Position=[100 100 720 540]);
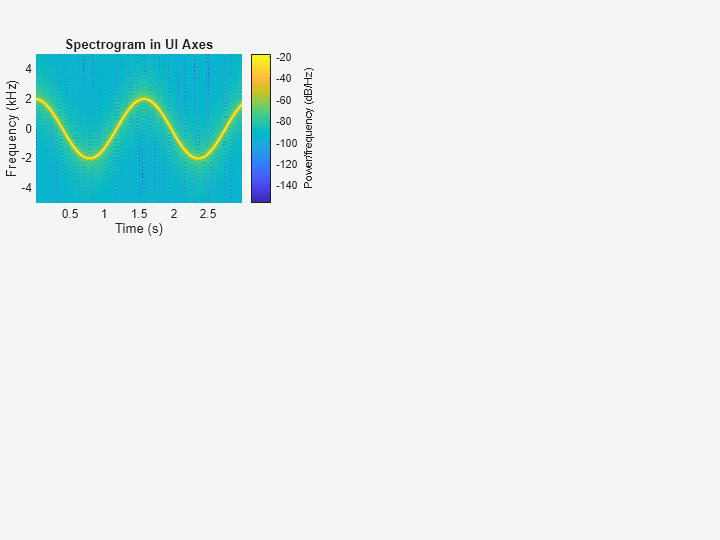
ax3 = uiaxes(uif,'Position',[5 305 300 200]);信号 x3 の PSD 推定を Figure の座標軸にプロットします。周波数を y 軸に表示し、0 kHz を中心とします。
spectrogram(x3,g,ol,nfft,Fs,"centered","yaxis",Parent=ax3); title(ax3,"Spectrogram in UI Axes")
パネル コンテナーへのスペクトログラムのプロット
UI Figure ウィンドウの南東隅にパネル コンテナーを追加します。
ax4 = uipanel(uif,Position=[300 5 400 325], ... Title="Spectrogram in UI Panel", ... BackgroundColor="white");
信号 x4 の PSD 推定をパネル コンテナーにプロットします。周波数を y 軸に表示します。
spectrogram(x4,g,ol,nfft,Fs,"yaxis",Parent=ax4);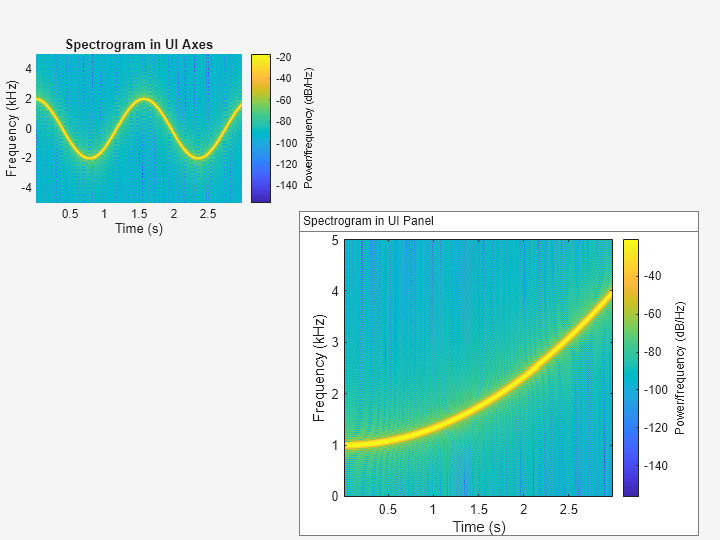
入力引数
入力信号。行ベクトルまたは列ベクトルとして指定します。
例: cos(pi/4*(0:159))+randn(1,160) は、ホワイト ガウス ノイズに含まれる正弦波を指定します。
データ型: single | double
複素数のサポート: あり
ウィンドウ。正の整数、あるいは行ベクトルまたは列ベクトルとして指定します。window は信号をセグメントに分割するために使用します。
windowが整数の場合、spectrogramはxを長さwindowのセグメントに分割し、各セグメントにその長さのハミング ウィンドウを適用します。windowがベクトルの場合、spectrogramはxをベクトルと同じ長さのセグメントに分割し、windowを使用して各セグメントにウィンドウを適用します。
x の長さが noverlap 個のオーバーラップ サンプルをもつ整数個のセグメントに厳密に分割できない場合、x はそれに応じた長さで打ち切られます。
window を空として指定した場合、spectrogram は、x が noverlap 個のオーバーラップ サンプルをもつ 8 個のセグメントに分割されているハミング ウィンドウを使用します。
利用可能なウィンドウのリストについては、ウィンドウを参照してください。
例: hann(N+1) と (1-cos(2*pi*(0:N)'/N))/2 は、いずれも長さ N + 1 のハン ウィンドウを指定します。
オーバーラップするサンプルの数。非負の整数として指定します。
windowがスカラーの場合、noverlapはwindowより小さくなければなりません。windowがベクトルの場合、noverlapはwindowの長さより小さくなければなりません。
noverlap を空として指定した場合、spectrogram はセグメント間で 50% のオーバーラップが発生する数を使用します。セグメントの長さを指定していない場合、関数により noverlap が ⌊Nx/4.5⌋ に設定されます。ここで、Nx は入力信号の長さで、⌊⌋ 記号は床関数を表します。
DFT 点の数。正の整数スカラーとして指定します。nfft を空として指定した場合、spectrogram によりパラメーターが max(256,2p) に設定されます。ここで p = ⌈log2 Nw⌉ で、⌈⌉ 記号は天井関数を表し、
windowがスカラーの場合は、Nw =windowです。windowがベクトルの場合は、Nw =length(です。window)
正規化周波数。ベクトルとして指定します。w は少なくとも 2 つの要素をもたなければなりません。そうでない場合は、関数が nfft として解釈するためです。正規化周波数の単位はラジアン/サンプルです。
例: pi./[2 4]
データ型: single | double
サンプル レート。正のスカラーで指定します。サンプル レートは単位時間あたりのサンプル数です。時間の単位が秒の場合、サンプル レートの単位は Hz です。
PSD 推定の周波数範囲。"onesided"、"twosided" または "centered" で指定します。実数値信号の場合、既定の設定は "onesided" です。複素数値信号の場合、既定の設定は "twosided" で、"onesided" を指定するとエラーになります。
"onesided"— 実数の入力信号の片側スペクトログラムを返します。nfftが偶数の場合、psはnfft/2 + 1 行をもち、計算区間は [0, π] ラジアン/サンプルです。nfftが奇数の場合、psは (nfft+ 1)/2 行をもち、計算区間は [0, π) ラジアン/サンプルです。fsを指定すると、それぞれの場合の計算区間は [0,fs/2] サイクル/単位時間、[0,fs/2) サイクル/単位時間となります。"twosided"— 実信号または複素数値信号の両側スペクトログラムを返します。psはnfft行をもち、計算区間は [0, 2π) ラジアン/サンプルです。fsを指定した場合、計算区間は [0,fs) サイクル/単位時間となります。"centered"— 中央に揃えた、実信号または複素数値信号の両側スペクトログラムを返します。psはnfft行をもちます。nfftが偶数の場合、psの計算区間は (–π, π] ラジアン/サンプルです。nfftが奇数の場合、psの計算区間は (–π, π) ラジアン/サンプルです。fsを指定すると、それぞれの場合の計算区間は (–fs/2,fs/2] サイクル/単位時間、(–fs/2,fs/2) サイクル/単位時間となります。
データ型: char | string
パワー スペクトルのスケーリング。"psd" または "power" で指定します。
spectrumtypeを省略するか、"psd"を指定すると、パワー スペクトル密度が返されます。"power"を指定すると、ウィンドウの等価ノイズ帯域幅ごとに PSD 推定をスケーリングします。結果は、各周波数のパワーの推定です。"reassigned"オプションがオンの場合、関数は、再代入の前に PSD を各周波数ビンの幅で積分します。
データ型: char | string
周波数の表示軸。"xaxis" または "yaxis" で指定します。
"xaxis"— 周波数が x 軸に、時間が y 軸に表示されます。"yaxis"— 周波数が y 軸に、時間が x 軸に表示されます。
この引数は出力引数で spectrogram を呼び出している場合に無視されます。
データ型: char | string
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
例: spectrogram(x,100,OutputTimeDimension="downrows") は x を長さ 100 のセグメントに分割し、各セグメントにその長さのハミング ウィンドウを適用します。スペクトログラムの出力には、行方向に沿った時間次元があります。
R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。
例: spectrogram(x,100,'OutputTimeDimension','downrows') は x を長さ 100 のセグメントに分割し、各セグメントにその長さのハミング ウィンドウを適用します。スペクトログラムの出力には、行方向に沿った時間次元があります。
しきい値。デシベル単位で表される実数スカラーとして指定します。spectrogram は、10 log10(s) ≤ thresh となる s の要素をゼロに設定します。
R2025a 以降
ターゲットとなる親。Axes オブジェクト、UIAxes オブジェクト、または Panel オブジェクトとして指定します。
Parentが指定された場合、spectrogram関数は、指定されたターゲットとなる親に PSD またはパワー スペクトルを表面プロットとしてプロットします。関数は、出力引数を指定して呼び出すかどうかにかかわらず、プロットを返します。Parentが指定されず、出力引数も指定されなかった場合、spectrogram関数は、gcaが返す現在の座標軸またはチャート上に PSD またはパワー スペクトルを表面プロットとしてプロットします。
ターゲットの詳細については、グラフィックス オブジェクトを参照してください。MATLAB® グラフィックスにおける親子関係の詳細については、グラフィックス オブジェクトの階層を参照してください。
データ型: Axes | UIAxes | Panel
出力引数
短時間フーリエ変換。行列として返されます。時間は s の列方向に、周波数は行方向に下がって 0 から増加します。
メモ
freqrange が "onesided" に設定されている場合、spectrogram は、正のナイキスト範囲の s 値を合計パワーを保存せずに出力します。
s は "reassigned" オプションの影響は受けません。
時点。ベクトルとして返されます。t の時間値は、各セグメントの中間点に対応します。
パワー スペクトル密度 (PSD) またはパワー スペクトル。行列として返されます。
xが実数でfreqrangeが指定されない場合、または"onesided"に設定されている場合、psは各セグメントの PSD またはパワー スペクトルの片側修正ピリオドグラム推定を含みます。この関数は 0 とナイキスト周波数以外のすべての周波数でパワーを 2 倍にして、合計パワーを保存します。xが複素数値の場合、もしくはfreqrangeが"twosided"または"centered"に設定されている場合、psは各セグメントの PSD またはパワー スペクトルの両側修正ピリオドグラム推定を含みます。wに正規化周波数のベクトルを指定した場合、またはfに巡回周波数のベクトルを指定した場合、psは入力周波数で評価された各セグメントの PSD またはパワー スペクトルの修正ピリオドグラム推定を含みます。
エネルギー中心の周波数および時間。短時間フーリエ変換と同じサイズの行列として返されます。サンプル レートを指定しない場合、fc の要素は正規化周波数として返されます。
詳細
短時間フーリエ変換 (STFT) を使用して、非定常信号の周波数成分が時間の経過と共に変化する様子を解析します。STFT の振幅の 2 乗は、信号の "スペクトログラム" 時間-周波数表現と呼ばれます。スペクトログラムの詳細や、関数 Signal Processing Toolbox™ を使用したスペクトログラムの計算方法については、Signal Processing Toolbox を使用したスペクトログラムの計算を参照してください。
信号の STFT は、信号上の長さ M の "解析ウィンドウ" g(n) をスライドして、ウィンドウ処理されたデータの各セグメントの離散フーリエ変換 (DFT) を計算することによって算出されます。ウィンドウは、R サンプルの間隔で元の信号を飛び越えます。これは、隣り合ったセグメント間の L = M – R 個のサンプルのオーバーラップに相当します。ほとんどのウィンドウ関数は、スペクトル リンギングを回避するためにエッジで小さくなります。ウィンドウ処理された各セグメントの DFT は、時間と周波数の各点の振幅と位相を含む複素数値行列に対して追加されます。STFT 行列は次の列数をもちます。
ここで、Nx は信号 x(n) の長さです。⌊⌋ 記号は床関数を表します。行列内の行数は、中央変換および両側変換の場合は DFT 点の数である NDFT と同じで、実数値信号の片側変換の場合は NDFT/2 に近い奇数に等しくなります。
STFT 行列 の m 番目の列には、時間 mR 付近を中心としたウィンドウが適用されたデータの DFT が含まれます。
ヒント
短時間フーリエ変換にゼロがある場合、デシベルに変換すると、プロットできない負の無限大になります。この問題の発生を避けるため、spectrogram を出力引数なしで呼び出した場合には短時間フーリエ変換に eps が加えられます。
参照
[1] Boashash, Boualem, ed. Time Frequency Signal Analysis and Processing: A Comprehensive Reference. Second edition. EURASIP and Academic Press Series in Signal and Image Processing. Amsterdam and Boston: Academic Press, 2016.
[2] Chassande-Motin, Éric, François Auger, and Patrick Flandrin. "Reassignment." In Time-Frequency Analysis: Concepts and Methods. Edited by Franz Hlawatsch and François Auger. London: ISTE/John Wiley and Sons, 2008.
[3] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.
[4] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. Second edition. Upper Saddle River, NJ: Prentice Hall, 1999.
[5] Rabiner, Lawrence R., and Ronald W. Schafer. Digital Processing of Speech Signals. Englewood Cliffs, NJ: Prentice-Hall, 1978.
拡張機能
spectrogram 関数は tall 配列をサポートしますが、次の使用上の注意と制限事項が伴います。
入力は tall 列ベクトルでなければなりません。
引数
windowは常に指定しなければなりません。OutputTimeDimensionは常に指定し、"downrows"に設定しなければなりません。reassignedオプションはサポートされません。出力引数のない構文はサポートされません。
詳細については、tall 配列を参照してください。
使用上の注意および制限:
Parent入力引数はサポートされていません。名前と値の引数を使用して指定する引数はコンパイル時の定数でなければなりません。
使用上の注意および制限:
名前と値の引数を使用して指定する引数はコンパイル時の定数でなければなりません。
可変サイズの
windowは倍精度でなければなりません。
この関数は、GPU 配列を完全にサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2006a より前に導入関数 spectrogram は、コード生成用の単精度可変サイズ ウィンドウ入力をサポートします。
関数 spectrogram は、単精度入力およびグラフィックス処理装置 (GPU) 用のコード生成をサポートします。CUDA® コードを生成するには、MATLAB Coder™ および GPU Coder™ が必要です。
[プロットの作成] ライブ エディター タスクを使用して、spectrogram の出力を対話的に可視化することができるようになりました。さまざまなグラフ タイプを選択し、オプションのパラメーターを設定できます。タスクは、ライブ スクリプトの一部となるコードも自動的に生成します。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)