periodogram

ピリオドグラム パワー スペクトル密度推定

構文

pxx = periodogram(x)

pxx = periodogram(x,window)

pxx = periodogram(x,window,nfft)

[pxx,w] = periodogram(___)

[pxx,f] = periodogram(___,fs)

[pxx,w] = periodogram(x,window,w)

[pxx,f] = periodogram(x,window,f,fs)

[___] = periodogram(x,window,___,freqrange)

[___,pxxc] = periodogram(___,'ConfidenceLevel',probability)

[rpxx,f] = periodogram(___,'reassigned')

[rpxx,f,pxx,fc] = periodogram(___,'reassigned')

[___] = periodogram(___,spectrumtype)

periodogram(___)

説明

pxx = periodogram(x) では、箱型ウィンドウを使用して検出された入力信号 x のピリオドグラム パワー スペクトル密度 (PSD) 推定 pxx が返されます。x がベクトルの場合、単一チャネルとして取り扱われます。x が行列の場合、PSD は列ごとに個別に計算され、pxx の対応する列に保存されます。x が実数値の場合、pxx は片側 PSD 推定です。x が複素数値の場合、pxx は両側 PSD 推定です。離散フーリエ変換 (DFT) の点の数 nfft の最大値は 256 または 信号長よりも大きい最小の 2 のべき乗です。

pxx = periodogram(x,window) では、ウィンドウ window を使用して、修正ピリオドグラム PSD 推定が返されます。window は、x と同じ長さのベクトルです。

pxx = periodogram(x,window,nfft) は、離散型フーリエ変換 (DFT) で nfft 個の点を使用します。nfft が信号長よりも大きい場合、x には長さ nfft までゼロが追加されます。nfft が信号長よりも小さい場合、信号は nfft を法としてラップされ、datawrap を使用して合計されます。たとえば、nfft が 4 の入力信号 [1 2 3 4 5 6 7 8] は、sum([1 5; 2 6; 3 7; 4 8],2) のピリオドグラムになります。

[pxx,w] = periodogram(___) では、正規化周波数ベクトル w が返されます。pxx が片側ピリオドグラムの場合、w は nfft が偶数であれば区間 [0,π] をカバーし、nfft が奇数であれば [0,π) をカバーします。pxx が両側ピリオドグラムの場合、w は区間 [0,2π) をカバーします。

[pxx,f] = periodogram(___,fs) は、周波数ベクトル f を単位時間あたりのサイクル数で返します。サンプル レート fs は単位時間あたりのサンプル数です。時間の単位が秒の場合、f の単位はサイクル/秒 (Hz) です。実数値の信号の場合、f は偶数の nfft に対しては区間 [0,fs/2] をカバーし、奇数の nfft に対しては [0,fs/2) をカバーします。複素数値の信号 f は区間 [0,fs) をカバーします。fs は periodogram の 4 番目の入力でなければなりません。サンプル レートを入力した場合でも、前のオプション引数の既定値を使用するには、これらの引数を空 [] として指定します。

[pxx,w] = periodogram(x,window,w) では、ベクトル w で指定される正規化周波数での両側ピリオドグラム推定が返されます。w には少なくとも 2 つの要素が含まれていなければなりません。そうでない場合は、関数が nfft として解釈するためです。

[pxx,f] = periodogram(x,window,f,fs) では、ベクトルで指定される周波数での両側ピリオドグラム推定が返されます。ベクトル f には少なくとも 2 つの要素が含まれていなければなりません。そうでない場合は、関数が nfft として解釈するためです。f の周波数の単位は単位時間あたりのサイクルです。サンプル レート fs は単位時間あたりのサンプル数です。時間の単位が秒の場合、f の単位はサイクル/秒 (Hz) です。

[___] = periodogram(x,window,___,freqrange) では、freqrange で指定される周波数範囲にわたるピリオドグラムが返されます。freqrange に指定できる有効なオプションは、'onesided'、'twosided' または 'centered' です。

[___,pxxc] = periodogram(___,'ConfidenceLevel',probability) では、PSD 推定の probability × 100% 信頼区間が pxxc で返されます。

[rpxx,f] = periodogram(___,'reassigned') では、各 PSD 推定が、そのエネルギーの中心に最も近い周波数に再代入されます。rpxx には f の各要素に再代入された推定の和が含まれます。

[rpxx,f,pxx,fc] = periodogram(___,'reassigned') は、再代入されない PSD 推定 pxx とエネルギー中心の周波数 fc も返します。'reassigned' フラグを使用する場合、probability 信頼区間は指定できません。

[___] = periodogram(___,spectrumtype) では、spectrumtype が 'psd' に指定されている場合は PSD 推定が返され、spectrumtype が 'power' に指定されている場合はパワー スペクトルが返されます。

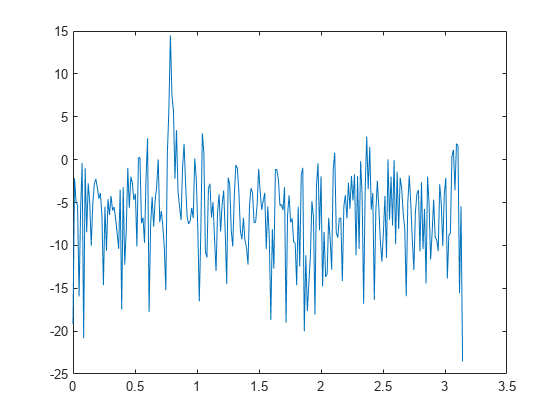
出力引数を設定せずに periodogram(___) を使用すると、現在の Figure ウィンドウにピリオドグラム PSD 推定またはパワー スペクトルがプロットされます。

例

既定の入力を使用したピリオドグラム

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルの離散時間正弦波で構成される入力信号のピリオドグラムを求めます。

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルの正弦波を作成します。信号長は 320 サンプルです。既定の箱型ウィンドウと DFT 長を使用してピリオドグラムを求めます。DFT 長は信号長よりも大きい最小の 2 のべき乗または 512 点です。信号は実数値で偶数の長さをもつため、ピリオドグラムは片側で 512/2+1 点を含みます。

n = 0:319;
x = cos(pi/4*n)+randn(size(n));
[pxx,w] = periodogram(x);
plot(w,10*log10(pxx))

出力なしで periodogram を使用してプロットを繰り返します。

periodogram(x)

ハミング ウィンドウを使用した修正ピリオドグラム

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルの離散時間正弦波で構成される入力信号の修正ピリオドグラムを求めます。

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルの正弦波を作成します。信号長は 320 サンプルです。ハミング ウィンドウと既定の DFT 長を使用して修正ピリオドグラムを求めます。DFT 長は信号長よりも大きい最小の 2 のべき乗または 512 点です。信号は実数値で偶数の長さをもつため、ピリオドグラムは片側で 512/2+1 点を含みます。

n = 0:319;
x = cos(pi/4*n)+randn(size(n));
periodogram(x,hamming(length(x)))

信号長と等しい DFT 長

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルの離散時間正弦波で構成される入力信号のピリオドグラムを求めます。信号長と同じ DFT 長を使用します。

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルの正弦波を作成します。信号長は 320 サンプルです。既定の箱型ウィンドウと信号長と同じ DFT 長を使用してピリオドグラムを求めます。信号は実数値のため、既定では長さが 320/2+1 に等しい片側ピリオドグラムが返されます。

n = 0:319;
x = cos(pi/4*n)+randn(size(n));
nfft = length(x);
periodogram(x,[],nfft)

相対黒点数のピリオドグラム

1700 年から 1987 年にかけて毎年サンプリングされたウォルフ (相対黒点) 数データのピリオドグラムを求めます。

相対黒点数のデータを読み込みます。既定の箱型ウィンドウと DFT の点の数 (この例では 512) を使用してピリオドグラムを求めます。これらのデータのサンプル レートは 1 サンプル/年です。ピリオドグラムをプロットします。

load sunspot.dat
relNums=sunspot(:,2);

[pxx,f] = periodogram(relNums,[],[],1);

plot(f,10*log10(pxx))
xlabel('Cycles/Year')
ylabel('dB / (Cycles/Year)')
title('Periodogram of Relative Sunspot Number Data')

上の図から、およそ 0.1 サイクル/年にピリオドグラムのピークがあり、つまりおよそ 10 年が周期であることがわかります。

与えられた一連の正規化周波数におけるピリオドグラム

$$N(0,1)$$ 加法性ホワイト ノイズを伴う角周波数 $$\pi /4$$ ラジアン/サンプルと $$\pi /2$$ ラジアン/サンプルの 2 つの離散時間正弦波で構成される入力信号のピリオドグラムを求めます。$$\pi /4$$ および $$\pi /2$$ ラジアン/サンプルにおける両側ピリオドグラム推定を求めます。結果を片側ピリオドグラムと比較します。

n = 0:319;
x = cos(pi/4*n)+0.5*sin(pi/2*n)+randn(size(n));

[pxx,w] = periodogram(x,[],[pi/4 pi/2]);
pxx

pxx = 1×2

   14.0589    2.8872

[pxx1,w1] = periodogram(x);
plot(w1/pi,pxx1,w/pi,2*pxx,'o')
legend('pxx1','2 * pxx')
xlabel('\omega / \pi')

得られたピリオドグラムの値は片側ピリオドグラムの値の 1/2 です。特定の周波数のセットでピリオドグラムを評価する場合、出力は両側推定になります。

与えられた一連の巡回周波数におけるピリオドグラム

N(0,1) 加法性ホワイト ノイズを伴う周波数 100 Hz および 200 Hz の 2 つの正弦波で構成される信号を作成します。サンプリング周波数は 1 kHz です。100 Hz と 200 Hz における両側ピリオドグラムを求めます。

fs = 1000;
t = 0:0.001:1-0.001;
x = cos(2*pi*100*t)+sin(2*pi*200*t)+randn(size(t));

freq = [100 200];
pxx = periodogram(x,[],freq,fs)

pxx = 1×2

    0.2647    0.2313

95% 信頼限界の上限および下限

次の例は、ピリオドグラムでの信頼限界の使い方を示します。統計的有意性の必要条件ではありませんが、周囲の PSD 推定の信頼下限が信頼上限を超えるピリオドグラムの周波数は、時系列において有意な振幅を明確に示します。

N(0,1) 加法性ホワイト ノイズを伴う 100 Hz と 150 Hz の正弦波を重ね合わせて構成される信号を作成します。2 つの正弦波の振幅は 1 です。サンプリング周波数は 1 kHz です。

fs = 1000;
t = 0:1/fs:1-1/fs;
x = cos(2*pi*100*t) + sin(2*pi*150*t) + randn(size(t));

95% 信頼限界でピリオドグラム PSD 推定を求めます。信頼区間と共にピリオドグラムをプロットし、100 Hz と 150 Hz 付近の周波数関心領域を拡大します。

[pxx,f,pxxc] = periodogram(x,rectwin(length(x)),length(x),fs,...
    'ConfidenceLevel',0.95);

plot(f,10*log10(pxx))
hold on
plot(f,10*log10(pxxc),'-.')

xlim([85 175])
xlabel('Hz')
ylabel('dB/Hz')
title('Periodogram with 95%-Confidence Bounds')

100 および 150 Hz のごく近傍における信頼限界の下限は、100 および 150 Hz の近傍外における信頼限界の上限より大幅に上になります。

DC を中央に揃えたピリオドグラム

$$N(0,1)$$ 加法性ノイズを伴う 100 Hz の正弦波のピリオドグラムを求めます。データは 1 kHz でサンプリングされます。'centered' オプションを使用して DC を中央に揃えたピリオドグラムを求め、結果をプロットします。

fs = 1000;
t = 0:0.001:1-0.001;
x = cos(2*pi*100*t)+randn(size(t));
periodogram(x,[],length(x),fs,'centered')

再割り当てされたピリオドグラム

ホワイト ガウス ノイズに含まれる 200 Hz の正弦波で構成される信号を生成します。信号は 1 kHz で 1 秒間サンプリングされます。ノイズの分散は 0.01² です。再現可能な結果が必要な場合は、乱数発生器をリセットします。

rng('default')

Fs = 1000;
t = 0:1/Fs:1-1/Fs;
N = length(t);
x = sin(2*pi*t*200)+0.01*randn(size(t));

FFT を使用して、信号長で正規化された信号のパワー スペクトルを計算します。この正弦波はビン内にあるため、すべてのパワーは単一の周波数サンプルに集中しています。片側スペクトルをプロットします。ピークの近傍にズームインします。

q = fft(x,N);
ff = 0:Fs/N:Fs-Fs/N;

ffts = q*q'/N^2

ffts = 
0.4997

ff = ff(1:floor(N/2)+1);
q = q(1:floor(N/2)+1);

stem(ff,abs(q)/N,'*')
axis([190 210 0 0.55])

periodogram を使用して、信号のパワー スペクトルを計算します。ハン ウィンドウと 1024 の FFT 長を指定します。200 Hz における推定パワーと実際の値の割合差を求めます。

wind = hann(N);

[pun,fr] = periodogram(x,wind,1024,Fs,'power');

hold on
stem(fr,pun)

periodogErr = abs(max(pun)-ffts)/ffts*100

periodogErr = 
4.7349

パワー スペクトルを再度計算しますが、今度は再割り当てを使用します。新しい推定をプロットし、その最大値を FFT 値と比較します。

[pre,ft,pxx,fx] = periodogram(x,wind,1024,Fs,'power','reassigned');

stem(fx,pre)
hold off
legend('Original','Periodogram','Reassigned')

reassignErr = abs(max(pre)-ffts)/ffts*100

reassignErr = 
0.0779

正弦波のパワー推定

'power' オプションを使用して特定の周波数で正弦波のパワーを推定します。

1 kHz でサンプリングされた 1 秒間の 100 Hz 正弦波を作成します。正弦波の振幅は 1.8 で、これは 1.8²/2 = 1.62 のパワーと等しくなります。'power' オプションを使用してパワーを推定します。

fs = 1000;
t = 0:1/fs:1-1/fs;
x = 1.8*cos(2*pi*100*t);
[pxx,f] = periodogram(x,hamming(length(x)),length(x),fs,'power');
[pwrest,idx] = max(pxx);
fprintf('The maximum power occurs at %3.1f Hz\n',f(idx))

The maximum power occurs at 100.0 Hz

fprintf('The power estimate is %2.2f\n',pwrest)

The power estimate is 1.62

ピリオドグラムによるマルチチャネル信号の PSD 推定

$$N(0,1)$$ 加法性ホワイト ガウス ノイズを伴う 3 つの正弦波から構成されるマルチチャネル信号の 1024 サンプルを生成します。正弦波の周波数は、$$\pi /2$$、$$\pi /3$$、および $$\pi /4$$ ラジアン/サンプルです。ピリオドグラムを使用して信号の PSD を推定し、プロットします。

N = 1024;
n = 0:N-1;

w = pi./[2;3;4];
x = cos(w*n)' + randn(length(n),3);

periodogram(x)

生成した C コードを使用した修正ピリオドグラムの計算

ウィンドウを使用して、入力信号の修正ピリオドグラム パワー スペクトル密度 (PSD) 推定を返す関数 periodogram_data.m を作成します。この関数は、入力信号の長さと等しい離散フーリエ変換点の数を指定します。

type periodogram_data

function [pxx,f] = periodogram_data(inputData,window)
%#codegen
nfft = length(inputData);
[pxx,f] = periodogram(inputData,window,nfft);
end

codegen (MATLAB Coder)を使用して MEX 関数を生成します。

• この関数の %#codegen 命令は、MATLAB® コードがコード生成用であることを指定します。

• -args オプションは、MEX ファイルへの入力のサイズ、クラス、および実数/複素数を定義する引数の例を指定します。この例の場合、inputData を 1024 行 1 列の倍精度のランダム ベクトルとして指定し、window を長さ 1024 のハミング ウィンドウとして指定します。続く MEX 関数の呼び出しでは、1024 サンプルの入力信号とウィンドウを使用します。

• MEX 関数の名前を変更する場合は、-o オプションを使用します。

• コード生成レポートを表示するには、codegen コマンドの最後に -report オプションを追加します。

codegen periodogram_data -args {randn(1024,1),hamming(1024)}

Code generation successful.

関数 periodogram と生成した MEX 関数を使用して、1024 サンプルのノイズを含んだ正弦波の PSD 推定を計算します。$2\pi /5$ ラジアン/サンプルの正弦波正規化周波数とハン ウィンドウを指定します。2 つの推定をプロットして、両者が一致することを確認します。

N = 1024;
x = 2*cos(2*pi/5*(0:N-1)') + randn(N,1);
periodogram(x,hann(N))
[pxMex,fMex] = periodogram_data(x,hann(N));
hold on
plot(fMex/pi,pow2db(pxMex),':','Color',[0 0.4 0])
hold off
grid on
legend('periodogram','MEX function')

入力引数

x — 入力信号

ベクトル | 行列

行または列のベクトル、または行列として指定する入力信号。x が行列の場合、その各列は独立チャネルとして扱われます。

例: cos(pi/4*(0:159))+randn(1,160) は単一チャネルの行ベクトル信号です。

例: cos(pi./[4;2]*(0:159))'+randn(160,2) は 2 チャネル信号です。

データ型: single | double
複素数のサポート: あり

window — ウィンドウ

rectwin(length(x)) | kaiser(length(x),38) | ベクトル | []

ウィンドウ。入力信号と同じ長さの行ベクトルまたは列ベクトルで指定します。window を空として指定した場合、periodogram は箱型ウィンドウを使用します。'reassigned' フラグと空の window を指定した場合、関数は β = 38 のカイザー ウィンドウを使用します。

メモ

箱型ウィンドウの既定のサイドローブ減衰量は 13.3 dB です。この減衰は、この値 (ピーク スペクトル コンテンツを基準とする値) を下回るスペクトル コンテンツをマスクすることがあります。選択するウィンドウを変えることにより、分解能 (たとえば箱型ウィンドウを使用) とサイドローブ減衰量 (たとえばハン ウィンドウを使用) のバランスをとることができます。詳細については、ウィンドウ デザイナーを参照してください。

データ型: single | double

nfft — DFT 点の数

max(256,2^nextpow2(length(x))) (既定値) | 整数 | []

正の整数として指定する DFT 点の数。実数値の入力信号 x では、PSD 推定 pxx は、nfft が偶数の場合、長さ (nfft/2 + 1)、nfft が奇数の場合、長さ (nfft + 1)/2 になります。複素数値の入力信号 x では、PSD 推定は常に長さ nfft になります。nfft が空として指定されている場合、既定の nfft が使用されます。

データ型: single | double

fs — サンプル レート

正のスカラー

サンプル レート。正のスカラーで指定します。サンプル レートは単位時間あたりのサンプル数です。時間の単位が秒の場合、サンプル レートの単位は Hz です。

w — 正規化周波数

ベクトル

正規化周波数。少なくとも 2 つの要素をもつ行ベクトルまたは列ベクトルとして指定します。正規化周波数の単位はラジアン/サンプルです。

例: w = [pi/4 pi/2]

データ型: double | single

f — 周波数

ベクトル

周波数。少なくとも 2 つの要素をもつ行ベクトルまたは列ベクトルとして指定します。周波数の単位は単位時間あたりのサイクルです。単位時間はサンプル レート fs で指定されます。fs の単位がサンプル/秒であれば、f の単位は Hz です。

例: fs = 1000; f = [100 200]

データ型: double | single

freqrange — PSD 推定の周波数範囲

'onesided' | 'twosided' | 'centered'

'onesided'、'twosided' または 'centered' で指定する、PSD 推定の周波数範囲。既定値は、実数値信号の場合は 'onesided'、複素数値信号の場合は 'twosided' です。各オプションに対応する周波数範囲は次のとおりです。

• 'onesided' — 実数値入力信号 x の片側 PSD を返します。nfft が偶数の場合、pxx の長さは nfft/2 + 1 で、計算区間は [0,π] ラジアン/サンプルです。nfft が奇数の場合、pxx の長さは (nfft + 1)/2、区間は [0,π) ラジアン/サンプルです。fs がオプションで指定されると、対応する区間はそれぞれ、nfft が偶数の場合は [0,fs/2] サイクル/単位時間、奇数の場合は [0,fs/2) サイクル/単位時間になります。

  この関数は 0 とナイキスト周波数以外のすべての周波数でパワーを 2 倍にして、合計パワーを保存します。

• 'twosided' — 実数値または複素数値の入力 x について両側 PSD 推定を返します。この場合、pxx の長さは nfft、計算区間は [0,2π) ラジアン/サンプルです。fs がオプションで指定される場合、その区間は [0,fs) サイクル/単位時間になります。

• 'centered' — 実数値または複素数値の入力 x について中央に揃えた両側 PSD 推定を返します。この場合、pxx の長さは nfft、偶数長の nfft については区間 (–π,π] ラジアン/サンプルで、奇数長の nfft については (–π,π) ラジアン/サンプルで計算されます。fs がオプションで指定されると、対応する区間はそれぞれ、nfft が偶数長の場合は (–fs/2,fs/2] サイクル/単位時間、奇数長の場合は (–fs/2,fs/2) サイクル/単位時間になります。

入力として周波数のベクトル w または f と freqrange を指定した場合、periodogram は freqrange を無視します。

データ型: char | string

spectrumtype — パワー スペクトルのスケーリング

'psd' (既定値) | 'power'

パワー スペクトルのスケーリング。'psd' または 'power' で指定します。パワー スペクトル密度を返すには、spectrumtype を省略するか、または 'psd' を指定します。各周波数のパワーの推定を求めるには、代わりに 'power' を使用します。'power' を指定すると、'reassigned' フラグを使用している場合を除き、ウィンドウ相当ノイズ帯域幅ごとの PSD 推定をスケーリングします。

データ型: char | string

probability — PSD 推定の信頼区間

0.95 (既定値) | (0,1) の範囲のスカラー

(0,1) の範囲のスカラーとして指定する、真の PSD のカバレッジ確率。出力 pxxc は真の PSD の probability × 100% 区間推定の下限および上限を含みます。

出力引数

pxx — PSD 推定

ベクトル | 行列

PSD 推定。実数値の非負の列ベクトルまたは行列として返されます。pxx の各列が x の対応する列の PSD 推定です。PSD 推定の単位は、単位周波数あたりの時系列データの 2 乗振幅単位となります。たとえば、入力データがボルト単位の場合、PSD 推定の単位は単位周波数あたりのボルトの 2 乗となります。ボルト単位の時系列では、抵抗が 1 Ω という想定でサンプル レートをヘルツで指定した場合、PSD 推定はワット/ヘルツ単位となります。

f — 巡回周波数

ベクトル

巡回周波数。実数値の列ベクトルとして返されます。片側 PSD 推定では、f は nfft が偶数の場合は区間 [0,fs/2] をカバーし、nfft が奇数の場合は [0,fs/2) をカバーします。両側 PSD 推定では、f は区間 [0,fs) をカバーします。DC を中央に揃えた PSD 推定では、f は、nfft が偶数長であれば区間 (-fs/2, fs/2] サイクル/単位時間をカバーし、nfft が奇数長であれば (-fs/2, fs/2) サイクル/単位時間をカバーします。

w — 正規化周波数

ベクトル

正規化周波数。実数値の列ベクトルとして返されます。pxx が片側 PSD 推定の場合、w は偶数の nfft に対しては区間 [0,π] をカバーし、奇数の nfft に対しては [0,π) をカバーします。pxx が両側 PSD 推定の場合、w は区間 [0,2π) をカバーします。DC を中央に揃えた PSD 推定の場合、nfft が偶数のときは w は区間 (–π,π] をカバーし、nfft が奇数のときは (–π,π) をカバーします。

pxxc — 信頼限界

行列

信頼限界。実数値要素をもつ行列として返されます。行列の行のサイズは、PSD 推定 pxx の長さと同じです。pxxc の列数は pxx の 2 倍です。奇数番号の列には信頼区間の下限が、偶数番号の列にはその上限がそれぞれ含まれています。したがって、pxxc(m,2*n-1) は、推定 pxx(m,n) に対応する信頼区間の下限で、pxxc(m,2*n) はその上限となります。信頼区間のカバレッジ確率は、probability の入力値によって決まります。

データ型: single | double

rpxx — 再代入された PSD 推定

ベクトル | 行列

再代入された PSD 推定。実数値の非負の列ベクトルまたは行列として返されます。rpxx の各列は、x の対応する列の再代入された PSD 推定です。

fc — エネルギー中心の周波数

ベクトル | 行列

エネルギー中心の周波数。ベクトルまたは行列として指定します。

詳細

ピリオドグラム

ピリオドグラムは広義定常性ランダム過程のパワー スペクトル密度 (PSD) のノンパラメトリック推定です。ピリオドグラムは自己相関列のバイアスのある推定のフーリエ変換です。fs サンプル/単位時間でサンプリングされた信号 x_n の場合、ピリオドグラムは次のように定義されます。

$$\widehat{P}(f)=\frac{\Delta t}{N}{\left|{\displaystyle \sum _{n=0}^{N-1}{x}_n}{e}^{-j2\pi f\Delta tn}\right|}^2,-1/2\Delta t<f\le 1/2\Delta t,$$

ここで、Δt はサンプリング間隔です。片側ピリオドグラムの場合、0 とナイキスト周波数 1/2Δt 以外のすべての周波数における値は、合計パワーを保全するため 2 倍されます。

周波数の単位がラジアン/サンプルの場合、ピリオドグラムは次のように定義されます。

$$\widehat{P}(\omega )=\frac{1}{2\pi N}{\left|{\displaystyle \sum _{n=0}^{N-1}{x}_n}{e}^{-j\omega n}\right|}^2,-\pi <\omega \le \pi .$$

上記の方程式の周波数範囲は freqrange 引数の値によって異なります。入力引数の freqrange の説明を参照してください。

1 周期 (巡回周波数の場合は 1/Δt、正規化周波数の場合は 2π) に対する真の PSD の積分 (P(f)) は、広義定常ランダム過程の分散に等しくなります。

$${\sigma }^2={\displaystyle {\int }_{-1/2\Delta t}^{1/2\Delta t}P}(f)df.$$

正規化周波数の場合は、積分範囲を適切に置き換えます。

修正ピリオドグラム

修正ピリオドグラムは、入力時系列をウィンドウ関数で乗算します。適切なウィンドウ関数は非負であり、開始点と終了点でゼロに減衰します。時系列をウィンドウ関数で乗算すると、データが徐々に断続的に "漸減し"、ピリオドグラムでの漏れを軽減します。例については、ピリオドグラムにおけるバイアスとばらつきを参照してください。

h_n がウィンドウ関数の場合、修正ピリオドグラムは次のように定義されます。

$$\widehat{P}(f)=\frac{\Delta t}{N}{\left|{\displaystyle \sum _{n=0}^{N-1}{h}_n}{x}_n{e}^{-j2\pi f\Delta tn}\right|}^2,-1/2\Delta t<f\le 1/2\Delta t,$$

ここで、Δt はサンプリング間隔です。

周波数の単位がラジアン/サンプルの場合、修正ピリオドグラムは次のように定義されます。

$$\widehat{P}(\omega )=\frac{1}{2\pi N}{\left|{\displaystyle \sum _{n=0}^{N-1}{h}_n}{x}_n{e}^{-j\omega n}\right|}^2,-\pi <\omega \le \pi .$$

上記の方程式の周波数範囲は freqrange 引数の値によって異なります。入力引数の freqrange の説明を参照してください。

再割り当てされたピリオドグラム

再割り当て手法では、スペクトル推定の局所化が鮮明になり、読み取りと解釈の容易なピリオドグラムが作成されます。この手法では、各 PSD 推定はビンの幾何学的中心から離れ、そのビンのエネルギー中心に再代入されます。これにより、チャープとインパルスの厳密な局所化が行われます。

参照

[1] Auger, François, and Patrick Flandrin. "Improving the Readability of Time-Frequency and Time-Scale Representations by the Reassignment Method." IEEE^® Transactions on Signal Processing. Vol. 43, May 1995, pp. 1068–1089.

[2] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

R2024a: 単精度可変サイズ ウィンドウ入力のためのコード生成サポート

関数 periodogram は、コード生成用の単精度可変サイズ ウィンドウ入力をサポートします。

R2024a: periodogram は GPU コード生成をサポートする

関数 periodogram は、グラフィックス処理装置 (GPU) 用のコード生成をサポートします。CUDA^® コードを生成するには、MATLAB^® Coder™ および GPU Coder™ が必要です。

R2023b: 単精度データの使用

関数 periodogram は単精度入力をサポートします。

R2023a: [プロットの作成] ライブ エディター タスクを使用した関数出力の可視化

[プロットの作成] ライブ エディター タスクを使用して、periodogram の出力を対話的に可視化することができるようになりました。さまざまなグラフ タイプを選択し、オプションのパラメーターを設定できます。タスクは、ライブ スクリプトの一部となるコードも自動的に生成します。

参考

アプリ

• 信号アナライザー

関数

• bandpower | pcov | pburg | plomb | pmcov | pmtm | pspectrum | pwelch | sfdr

トピック

• ピリオドグラムにおけるバイアスとばらつき
• FFT を使用したパワー スペクトル密度推定
• ノンパラメトリック法