Main Content

このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

pburg

自己回帰パワー スペクトル密度の推定 — バーグ法

ページ内をすべて折りたたむ

構文

pxx = pburg(x,order)
pxx = pburg(x,order,nfft)
[pxx,w] = pburg(___)
[pxx,f] = pburg(___,fs)
[pxx,w] = pburg(x,order,w)
[pxx,f] = pburg(x,order,f,fs)
[___] = pburg(x,order,___,freqrange)
[___,pxxc] = pburg(___,'ConfidenceLevel',probability)
pburg(___)

説明

pxx = pburg(x,order) では、バーグ法を使用して求められた 離散時間信号 x のパワー スペクトル密度 (PSD) 推定 pxx が返されます。x がベクトルの場合、単一チャネルとして取り扱われます。x が行列の場合、PSD は列ごとに個別に計算され、pxx の対応する列に保存されます。pxx は単位周波数あたりのパワーの分布です。周波数はラジアン/サンプルの単位で表されます。order は PSD 推定の生成に使用する AR (自己回帰) モデルの次数です。

pxx = pburg(x,order,nfft) は、離散型フーリエ変換 (DFT) で nfft 個の点を使用します。x が実数の場合、pxx の長さは、nfft が偶数であれば (nfft/2+1)、nfft が奇数であれば (nfft+1)/2 になります。複素数値の x の場合、pxx は常に長さ nfft になります。nfft を省略するか、空として指定した場合、pburg は既定の DFT の長さ 256 を使用します。

例

[pxx,w] = pburg(___) は正規化された角周波数のベクトル w を返し、PSD はその周波数で推定されます。w の単位はラジアン/サンプルです。実数値の信号の場合、w は nfft が偶数であれば区間 [0,π] をカバーし、nfft が奇数であれば [0,π) をカバーします。複素数値の信号の場合、w は常に区間 [0,2π) をカバーします。

[pxx,f] = pburg(___,fs) は、周波数ベクトル f を単位時間あたりのサイクル数で返します。サンプリング周波数 fs は単位時間あたりのサンプル数です。時間の単位が秒の場合、f の単位はサイクル/秒 (Hz) です。実数値の信号の場合、f は偶数の nfft に対しては区間 [0,fs/2] をカバーし、奇数の nfft に対しては [0,fs/2) をカバーします。複素数値の信号 f は区間 [0,fs) をカバーします。fs は pburg の 4 番目の入力でなければなりません。サンプル レートを入力した場合でも前のオプション引数の既定値を使用するには、これらの引数を空 [] として指定します。

例

[pxx,w] = pburg(x,order,w) は、ベクトル w で指定される正規化周波数での両側 AR PSD 推定を返します。ベクトル w には少なくとも 2 つの要素が含まれていなければなりません。そうでない場合は、関数が nfft として解釈するためです。

[pxx,f] = pburg(x,order,f,fs) は、ベクトル f で指定される周波数での両側 AR PSD 推定を返します。ベクトル f には少なくとも 2 つの要素が含まれていなければなりません。そうでない場合は、関数が nfft として解釈するためです。f の周波数の単位は単位時間あたりのサイクルです。サンプリング周波数 fs は単位時間あたりのサンプル数です。時間の単位が秒の場合、f の単位はサイクル/秒 (Hz) です。

[___] = pburg(x,order,___,freqrange) は、freqrange で指定される周波数範囲での AR PSD 推定を返します。freqrange に指定できる有効なオプションは、'onesided'、'twosided' または 'centered' です。

[___,pxxc] = pburg(___,'ConfidenceLevel',probability) では、PSD 推定の probability × 100% 信頼区間が pxxc で返されます。

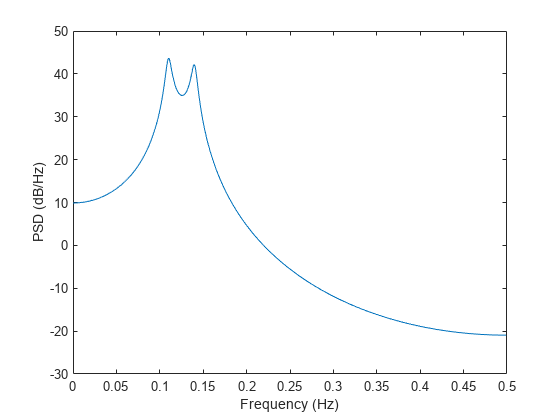
出力引数なしで pburg(___) を使用すると、現在の Figure ウィンドウに、AR PSD 推定が単位周波数あたりの dB 単位でプロットされます。

例

例

すべて折りたたむ

ライブ スクリプトを開く

AR(4) 広義定常性ランダム過程の実現を作成します。バーグ法を使用して PSD を推定します。単一の実現に基づく PSD 推定を、ランダム過程の実際の PSD と比較します。

AR(4) システム関数を作成します。周波数応答を取得してシステムの PSD をプロットします。

A = [1 -2.7607 3.8106 -2.6535 0.9238];
[H,F] = freqz(1,A,[],1);
plot(F,20*log10(abs(H)))

xlabel('Frequency (Hz)')
ylabel('PSD (dB/Hz)')

AR(4) ランダム過程の実現を作成します。再現性のある結果を得るために、乱数発生器を既定の状態に設定します。実現の長さは 1000 サンプルです。サンプリング周波数は 1 Hz であると仮定します。pburg を使用して 4 次の過程の PSD を推定します。PSD 推定を実際の PSD と比較します。

rng default

x = randn(1000,1);
y = filter(1,A,x);
[Pxx,F] = pburg(y,4,1024,1);

hold on
plot(F,10*log10(Pxx))
legend('True Power Spectral Density','pburg PSD Estimate')

ライブ スクリプトを開く

AR(4) 過程の実現を作成します。arburg を使用して反射係数を決定します。この反射係数を使用して、過程に対し適切な AR モデルの次数を決定します。過程 PSD の推定を取得します。

長さが 1000 サンプルの AR(4) 過程の実現を作成します。次数を 12 に設定して arburg を使用し、反射係数を返します。反射係数をプロットして、適切なモデル次数を決定します。

A = [1 -2.7607 3.8106 -2.6535 0.9238];

rng default

x = filter(1,A,randn(1000,1));

[a,e,k] = arburg(x,12);

stem(k,'filled')
title('Reflection Coefficients')
xlabel('Model Order')

反射係数は次数 4 の後にゼロまで減衰します。これは AR(4) モデルが最適であることを示しています。

バーグ法を使用してランダム過程の PSD 推定を取得します。DFT で 1000 個の点を使用します。PSD 推定をプロットします。

pburg(x,4,length(x))

ライブ スクリプトを開く

N(0,1) 加法性ホワイト ガウス ノイズを伴う 3 個の正弦波から構成されるマルチチャネル信号を作成します。正弦波の周波数は 100 Hz、200 Hz および 300 Hz です。サンプリング周波数は 1 kHz で、信号は 1 秒間持続します。

Fs = 1000;

t = 0:1/Fs:1-1/Fs;

f = [100;200;300];

x = cos(2*pi*f*t)'+randn(length(t),3);

バーグ法を使用して 12 次の自己回帰モデルにより信号の PSD を推定します。既定の DFT 長を使用します。推定をプロットします。

morder = 12;

pburg(x,morder,[],Fs)

入力引数

すべて折りたたむ

行または列のベクトル、または行列として指定する入力信号。x が行列の場合、その各列は独立チャネルとして扱われます。

例: cos(pi/4*(0:159))+randn(1,160) は単一チャネルの行ベクトル信号です。

例: cos(pi./[4;2]*(0:159))'+randn(160,2) は 2 チャネル信号です。

データ型: single | double
複素数のサポート: あり

正の整数として指定される、自動回帰モデルの次数。

データ型: double

正の整数として指定する DFT 点の数。実数値の入力信号 x では、PSD 推定 pxx は、nfft が偶数の場合、長さ (nfft/2+1)、nfft が奇数の場合、長さ (nfft+1)/2 になります。複素数値の入力信号 x では、PSD 推定は常に長さ nfft になります。nfft が空として指定されている場合、既定の nfft が使用されます。

データ型: single | double

サンプル レート。正のスカラーで指定します。サンプル レートは単位時間あたりのサンプル数です。時間の単位が秒の場合、サンプル レートの単位は Hz です。

正規化周波数。少なくとも 2 つの要素をもつ行ベクトルまたは列ベクトルとして指定します。正規化周波数の単位はラジアン/サンプルです。

例: w = [pi/4 pi/2]

データ型: double | single

周波数。少なくとも 2 つの要素をもつ行ベクトルまたは列ベクトルとして指定します。周波数の単位は単位時間あたりのサイクルです。単位時間はサンプル レート fs で指定されます。fs の単位がサンプル/秒であれば、f の単位は Hz です。

例: fs = 1000; f = [100 200]

データ型: double | single

'onesided'、'twosided' または 'centered' で指定する、PSD 推定の周波数範囲。既定値は、実数値信号の場合は 'onesided'、複素数値信号の場合は 'twosided' です。各オプションに対応する周波数範囲は次のとおりです。

  • 'onesided' — 実数値入力信号 x の片側 PSD を返します。nfft が偶数の場合、pxx の長さは nfft/2 + 1 で、計算区間は [0,π] ラジアン/サンプルです。nfft が奇数の場合、pxx の長さは (nfft + 1)/2、区間は [0,π) ラジアン/サンプルです。fs がオプションで指定されると、対応する区間はそれぞれ、nfft が偶数の場合は [0,fs/2] サイクル/単位時間、奇数の場合は [0,fs/2) サイクル/単位時間になります。

    この関数は 0 とナイキスト周波数以外のすべての周波数でパワーを 2 倍にして、合計パワーを保存します。

  • 'twosided' — 実数値または複素数値の入力 x について両側 PSD 推定を返します。この場合、pxx の長さは nfft、計算区間は [0,2π) ラジアン/サンプルです。fs がオプションで指定される場合、その区間は [0,fs) サイクル/単位時間になります。

  • 'centered' — 実数値または複素数値の入力 x について中央に揃えた両側 PSD 推定を返します。この場合、pxx の長さは nfft、偶数長の nfft については区間 (–π,π] ラジアン/サンプルで、奇数長の nfft については (–π,π) ラジアン/サンプルで計算されます。fs がオプションで指定されると、対応する区間はそれぞれ、nfft が偶数長の場合は (–fs/2,fs/2] サイクル/単位時間、奇数長の場合は (–fs/2,fs/2) サイクル/単位時間になります。

データ型: char | string

(0,1) の範囲のスカラーとして指定する、真の PSD のカバレッジ確率。出力 pxxc は真の PSD の probability × 100% 区間推定の下限および上限を含みます。

出力引数

すべて折りたたむ

PSD 推定。実数値の非負の列ベクトルまたは行列として返されます。pxx の各列が x の対応する列の PSD 推定です。PSD 推定の単位は、単位周波数あたりの時系列データの 2 乗振幅単位となります。たとえば、入力データがボルト単位の場合、PSD 推定の単位は単位周波数あたりのボルトの 2 乗となります。ボルト単位の時系列では、抵抗が 1 Ω という想定でサンプル レートをヘルツで指定した場合、PSD 推定はワット/ヘルツ単位となります。

正規化周波数。実数値の列ベクトルとして返されます。pxx が片側 PSD 推定の場合、w は偶数の nfft に対しては区間 [0,π] をカバーし、奇数の nfft に対しては [0,π) をカバーします。pxx が両側 PSD 推定の場合、w は区間 [0,2π) をカバーします。DC を中央に揃えた PSD 推定の場合、nfft が偶数のときは w は区間 (–π,π] をカバーし、nfft が奇数のときは (–π,π) をカバーします。

巡回周波数。実数値の列ベクトルとして返されます。片側 PSD 推定では、f は nfft が偶数の場合は区間 [0,fs/2] をカバーし、nfft が奇数の場合は [0,fs/2) をカバーします。両側 PSD 推定では、f は区間 [0,fs) をカバーします。DC を中央に揃えた PSD 推定では、f は、nfft が偶数長であれば区間 (-fs/2, fs/2] サイクル/単位時間をカバーし、nfft が奇数長であれば (-fs/2, fs/2) サイクル/単位時間をカバーします。

信頼限界。実数値要素をもつ行列として返されます。行列の行のサイズは、PSD 推定 pxx の長さと同じです。pxxc の列数は pxx の 2 倍です。奇数番号の列には信頼区間の下限が、偶数番号の列にはその上限がそれぞれ含まれています。したがって、pxxc(m,2*n-1) は、推定 pxx(m,n) に対応する信頼区間の下限で、pxxc(m,2*n) はその上限となります。信頼区間のカバレッジ確率は、probability の入力値によって決まります。

データ型: single | double

拡張機能

バージョン履歴

R2006a より前に導入

参考

| |