plomb
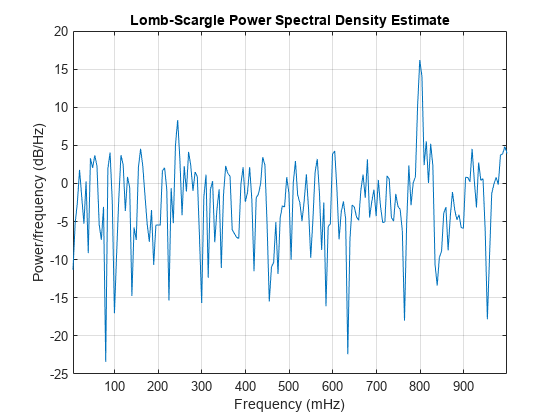
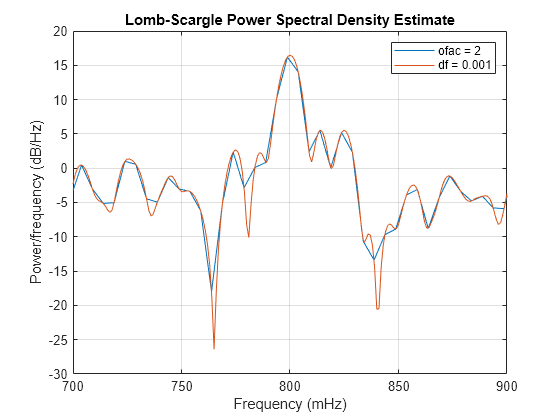
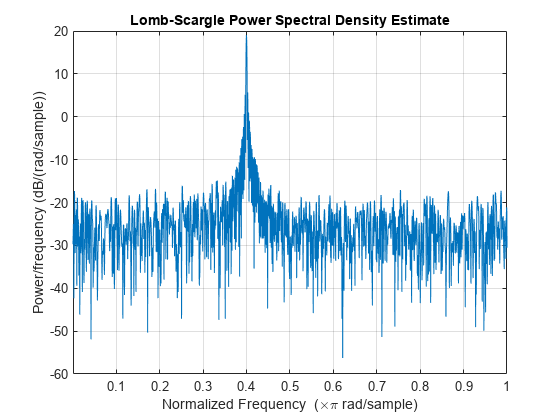
Lomb-Scargle ピリオドグラム
構文
説明
[ では、pxx,f] = plomb(x,t)t で指定された時点でサンプリングされた信号 x の Lomb-Scargle パワー スペクトル密度 (PSD) 推定 pxx が返されます。t は単調増加しなければなりませんが、その間隔は均一である必要はありません。t のすべての要素が非負でなければなりません。pxx は f で返される周波数で評価されます。
xがベクトルの場合、単一チャネルとして取り扱われます。xが行列の場合、plombは各列の PSD を個別に計算し、結果を対応するpxxの列に返します。
x または t には NaN または NaT が含まれることがあります。これらの値は欠損データとして取り扱われ、スペクトルの計算からは除外されます。
出力引数を設定せずに plomb(___) を使用すると、現在の Figure ウィンドウに Lomb-Scargle ピリオドグラム PSD 推定がプロットされます。
例
入力引数
出力引数
詳細
参照
[1] Horne, James H., and Sallie L. Baliunas. "A Prescription for Period Analysis of Unevenly Sampled Time Series." Astrophysical Journal. Vol. 302, 1986, pp. 757–763.
[2] Lomb, Nicholas R. "Least-Squares Frequency Analysis of Unequally Spaced Data." Astrophysics and Space Science. Vol. 39, 1976, pp. 447–462.
[3] Press, William H., and George B. Rybicki. "Fast Algorithm for Spectral Analysis of Unevenly Sampled Data." Astrophysical Journal. Vol. 338, 1989, pp. 277–280.
[4] Scargle, Jeffrey D. "Studies in Astronomical Time Series Analysis. II. Statistical Aspects of Spectral Analysis of Unevenly Spaced Data." Astrophysical Journal. Vol. 263, 1982, pp. 835–853.
拡張機能
バージョン履歴
R2014b で導入