このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

ピリオドグラムにおけるバイアスとばらつき

この例では、ピリオドグラムにおけるバイアスとばらつきを減らす方法を示します。ウィンドウを使用すると、ピリオドグラムにおけるバイアスを減らすことができます。また、平均化機能のあるウィンドウを使用してばらつきを減らすことができます。

広義定常性自己回帰 (AR) 過程を使用して、ピリオドグラムにおけるバイアスとばらつきの影響を見ます。AR 過程は、その PSD が閉形式表現のため、扱いやすいモデルを提供します。次の形式の AR(2) モデルを作成します。

$$y(n)-0.75y(n-1)+0.5y(n-2)=\epsilon (n),$$

ここで、$$\epsilon (n)$$ は、いくつかの指定分散を持つゼロ平均のホワイト ノイズ列です。この例では、分散 1、サンプリング周期 1 と仮定します。上記の AR(2) 過程をシミュレートするには、全極 (IIR) フィルターを作成します。フィルターの振幅応答を表示します。

B2 = 1;
A2 = [1 -0.75 0.5];
fvtool(B2,A2)

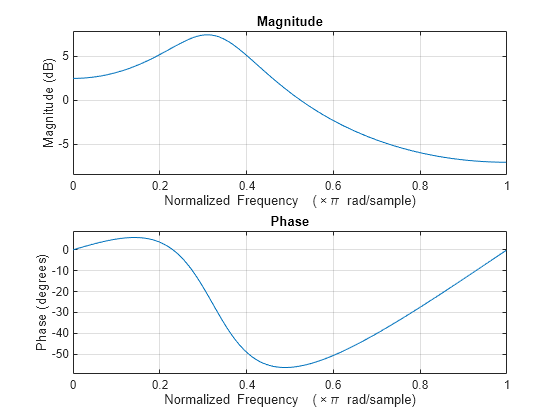
この過程はバンドパスです。PSD のダイナミック レンジは約 14.5 dB で、これは次のコードで算出できます。

[H2,W2] = freqz(B2,A2,1e3,1);
dr2 = max(20*log10(abs(H2)))-min(20*log10(abs(H2)))

dr2 = 14.4984

極の配置を調べることによって、この AR(2) 過程が安定であることがわかります。2 つの極は単位円の中にあります。

fvtool(B2,A2,'Analysis','polezero')

次に、以下の式で表される AR(4) 過程を作成します。

$$y(n)-2.7607y(n-1)+3.8106y(n-2)-2.6535y(n-3)+0.9238y(n-4)=\epsilon (n).$$

次のコードを使用して、この IIR システムの振幅応答を表示します。

B4 = 1;
A4 = [1 -2.7607 3.8106 -2.6535 0.9238];
fvtool(B4,A4)

極の配置を調べることによって、この AR(4) 過程も安定であることがわかります。4 つの極は単位円の中にあります。

fvtool(B4,A4,'Analysis','polezero')

この PSD のダイナミック レンジは約 65 dB で、AR(2) モデルよりはるかに大きな値です。

[H4,W4] = freqz(B4,A4,1e3,1);
dr4 = max(20*log10(abs(H4)))-min(20*log10(abs(H4)))

dr4 = 64.6213

これらの AR(p) 過程からの実現をシミュレートするには、randn と filter を使用します。結果に再現性をもたせるために、乱数発生器を既定の設定にします。実現をプロットします。

rng default
x = randn(1e3,1);
y2 = filter(B2,A2,x);
y4 = filter(B4,A4,x);

subplot(2,1,1)
plot(y2)
title('AR(2) Process')
xlabel('Time')

subplot(2,1,2)
plot(y4)
title('AR(4) Process')
xlabel('Time')

AR(2) および AR(4) 実現のピリオドグラムを計算してプロットします。結果を実際の PSD と比較します。periodogram により周波数が mHz に変換されてプロットされていることに注意してください。

Fs = 1;
NFFT = length(y2);

subplot(2,1,1)
periodogram(y2,rectwin(NFFT),NFFT,Fs)
hold on
plot(1000*W2,20*log10(abs(H2)),'r','linewidth',2)
title('AR(2) PSD and Periodogram')

subplot(2,1,2)
periodogram(y4,rectwin(NFFT),NFFT,Fs)
hold on
plot(1000*W4,20*log10(abs(H4)),'r','linewidth',2)
title('AR(4) PSD and Periodogram')
text(350,20,'\downarrow Bias')

AR(2) 過程の場合、ピリオドグラム推定は真の PSD の形状に従いますが、かなりのばらつきを示します。これは、自由度が小さいことによるものです。ピリオドグラムにおける顕著な負の偏差 (dB) は、自由度 2 のカイ二乗確率変数の対数を取ることにより説明されます。

AR(4) 過程の場合、ピリオドグラムは低周波数では真の PSD の形状に従いますが、高周波数では真の PSD から逸脱しています。これはフェイェール核を伴う畳み込みの影響です。AR(2) 過程に比べて AR(4) 過程の大きなダイナミック レンジは、バイアスをより顕著にするものです。

AR(4) 過程内に示されたバイアスをテーパーまたはウィンドウを使用して緩和します。この例では、ピリオドグラムを求める前に、ハミング ウィンドウを使用して AR(4) 実現にテーパーをかけます。

figure
periodogram(y4,hamming(length(y4)),NFFT,Fs)
hold on
plot(1000*W4,20*log10(abs(H4)),'r','linewidth',2)
title('AR(4) PSD and Periodogram with Hamming Window')
legend('Periodogram','AR(4) PSD')

ここで、ピリオドグラム推定は、ナイキスト周波数範囲全体で真の AR(4) PSD に従っていることに注意してください。ピリオドグラム推定は引き続き自由度 2 しかもたないため、ウィンドウを使用してもピリオドグラムのばらつきは低減されません。しかし、ウィンドウを使用することでバイアスは解決します。

ノンパラメトリック スペクトル推定において自由度を増やしてピリオドグラムのばらつきを低減する 2 つの方法は、ウェルチのオーバーラップ セグメント平均およびマルチテーパー スペクトル推定です。

時間と半帯域幅との積として 3.5 を使用して、AR(4) 時系列のマルチテーパー推定を求めます。結果をプロットします。

NW = 3.5;

figure
pmtm(y4,NW,NFFT,Fs)
hold on
plot(1000*W4,20*log10(abs(H4)),'r','linewidth',2)
legend('Multitaper Estimate','AR(4) PSD')

マルチテーパー法は、ピリオドグラムよりばらつきが大幅に少ない PSD 推定を生成します。マルチテーパー法もウィンドウを使用しているので、ピリオドグラムのバイアスも解決していることがわかります。

参考

periodogram | pmtm

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい