FFT を使用したパワー スペクトル密度推定
この例では、関数 periodogram および fft を使用して、等価なノンパラメトリック パワー スペクトル密度 (PSD) 推定を求める方法を示します。さまざまな事例において、偶数長の入力、正規化周波数およびヘルツ単位の周波数、片側および両側 PSD 推定に対し、fft の出力を適切にスケーリングする方法が示されます。どの事例でも箱型ウィンドウを使用します。
この例では、周波数成分が時間的に一定の定常信号に焦点を当てています。時間依存周波数成分をもつ非定常信号の場合、短時間フーリエ変換はより優れた解析ツールとなります。詳細については、Signal Processing Toolbox を使用したスペクトログラムの計算を参照してください。
サンプル レートを使用した偶数長の入力
fft と periodogram の両方を使用して、1 kHz でサンプリングされた偶数長の信号についてピリオドグラムを求めます。結果を比較します。
100 Hz 正弦波から成り、N(0,1) 加法性ノイズをもつ信号を作成します。サンプリング周波数は 1 kHz です。信号長は 1000 サンプルです。
fs = 1000; t = 0:1/fs:1-1/fs; x = cos(2*pi*100*t) + randn(size(t));
fft を使用してピリオドグラムを求めます。信号は実数値で、偶数長です。信号が実数値なので、正または負の周波数に対するパワー推定だけを必要とします。合計したパワーを保存するために、両セット (正および負の周波数) に現れているすべての周波数に係数 2 を乗算します。周波数 0 (DC) およびナイキスト周波数は、2 回は現れません。結果をプロットします。
N = length(x); xdft = fft(x); xdft = xdft(1:N/2+1); psdx = (1/(fs*N)) * abs(xdft).^2; psdx(2:end-1) = 2*psdx(2:end-1); freq = 0:fs/length(x):fs/2; plot(freq,pow2db(psdx)) grid on title("Periodogram Using FFT") xlabel("Frequency (Hz)") ylabel("Power/Frequency (dB/Hz)")

periodogram を使用してピリオドグラムを計算してプロットします。2 つの結果が同じであることを示します。
periodogram(x,rectwin(N),N,fs)

mxerr = max(psdx'-periodogram(x,rectwin(N),N,fs))
mxerr = 3.4694e-18
正規化された周波数を使用した入力
正規化周波数を使用した入力について、fft を使用してピリオドグラムを作成します。正弦波から成り、N(0,1) 加法性ノイズをもつ信号を作成します。この正弦波は ラジアン/サンプルの角周波数を持ちます。
N = 1000; n = 0:N-1; x = cos(pi/4*n) + randn(size(n));
fft を使用してピリオドグラムを求めます。信号は実数値で、偶数長です。信号が実数値なので、正または負の周波数に対するパワー推定だけを必要とします。合計したパワーを保存するために、両セット (正および負の周波数) に現れているすべての周波数に係数 2 を乗算します。周波数 0 (DC) およびナイキスト周波数は、2 回は現れません。結果をプロットします。
xdft = fft(x); xdft = xdft(1:N/2+1); psdx = (1/(2*pi*N)) * abs(xdft).^2; psdx(2:end-1) = 2*psdx(2:end-1); freq = 0:2*pi/N:pi; plot(freq/pi,pow2db(psdx)) grid on title("Periodogram Using FFT") xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Power/Frequency (dB/(rad/sample))")

periodogram を使用してピリオドグラムを計算してプロットします。2 つの結果が同じであることを示します。
periodogram(x,rectwin(N),N)

mxerr = max(psdx'-periodogram(x,rectwin(N),N))
mxerr = 4.4409e-16
正規化された周波数を使用した複素数値の入力
正規化周波数をもつ複素数値の入力について、fft を使用してピリオドグラムを作成します。信号は、複素数値の N(0,1) ノイズを伴う ラジアン/サンプルの角周波数を持つ複素指数です。
N = 1000; n = 0:N-1; x = exp(1j*pi/4*n) + [1 1j]*randn(2,N)/sqrt(2);
fft を使用してピリオドグラムを求めます。入力が複素数値であるため、 ラジアン/サンプルでピリオドグラムを求めます。結果をプロットします。
xdft = fft(x); psdx = (1/(2*pi*N)) * abs(xdft).^2; freq = 0:2*pi/N:2*pi-2*pi/N; plot(freq/pi,pow2db(psdx)) grid on title("Periodogram Using FFT") xlabel("Normalized Frequency (\times\pi rad/sample)") ylabel("Power/Frequency (dB/(rad/sample))")

periodogram を使用してピリオドグラムを求めてプロットします。PSD 推定を比較します。
periodogram(x,rectwin(N),N,"twosided")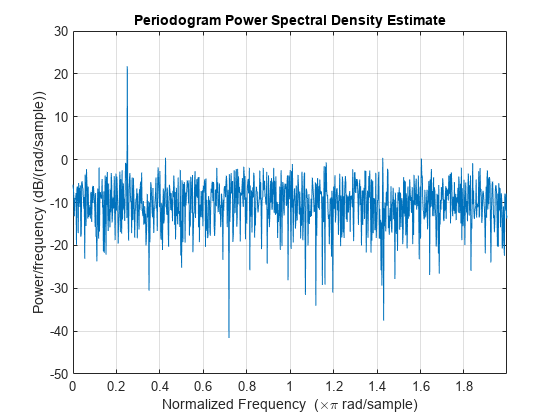
mxerr = max(psdx'-periodogram(x,rectwin(N),N,"twosided"))mxerr = 2.2204e-16
参考
アプリ
関数
fft|periodogram|pspectrum