時間-周波数解析の実践的基礎

時間-周波数解析を使用した DTMF 信号内の番号識別

ほとんどの時変信号は、それがどういったものでも各セクションの信号が実質的に定常的となる程度に短い区間に分割できます。時間-周波数解析では、信号をそういった短い時間にセグメント化し、複数のスライディング ウィンドウにわたってスペクトルを推定する方法が最も一般的です。pspectrum関数を "spectrogram" オプションと共に使用して、各スライディング ウィンドウ全体に対する FFT ベースのスペクトル推定を計算し、信号の周波数成分がどのように経時変化するかを可視化できます。

デジタル電話のダイヤルの信号伝達システムについて考えます。このようなシステムで生成される信号は、デュアルトーン多重周波数 (DTMF) 信号として知られています。ダイヤル番号ごとに生成される音は、互いに排他な 2 つのグループから取得された周波数をもつ 2 つの正弦波 $-$ またはトーン $-$ の和で構成されます。トーンの各ペアは、低群 (697 Hz、770 Hz、852 Hz または 941 Hz) の 1 つの周波数と高群 (1209 Hz、1336 Hz または 1477 Hz) の 1 つの周波数で構成され、固有のシンボルを表します。以下は電話パッドのボタンに割り当てられている周波数です。

DTMF 信号を生成して聞きます。

[tones, Fs] = helperDTMFToneGenerator();
p = audioplayer(tones,Fs,16);
play(p)

信号を聞くと、3 桁の番号がダイヤルされたことがわかります。ただし、どの番号かはわかりません。次に、650 ～ 1500 Hz 帯域の時間領域と周波数領域で信号を可視化します。pspectrum 関数の Leakage パラメーターを 1 に設定し、箱型ウィンドウを使用して周波数分解能を向上させます。

N = numel(tones);
t = (0:N-1)/Fs; 
subplot(2,1,1)
plot(1e3*t,tones)
xlabel("Time (ms)")
ylabel("Amplitude")
title("DTMF Signal")
subplot(2,1,2)
pspectrum(tones,Fs,Leakage=1,FrequencyLimits=[650, 1500])

信号の時間領域プロットでは、プッシュされた 3 つのボタンに対応して 3 つのエネルギーのバーストが存在することが確認できます。バーストの長さを測定するには、RMS 包絡線のパルス幅を取得します。

env = envelope(tones,80,"rms");
pulsewidth(env,Fs)

ans = 3×1

    0.1041
    0.1042
    0.1047

title("Pulse Width of RMS Envelope")

このように、それぞれにおいて約 100 ミリ秒の長さのパルスが 3 つ確認できます。ただし、どの番号がダイヤルされたのかはわかりません。周波数領域プロットでは信号に存在する周波数が示されるため、ダイヤルされた番号の判別に役立ちます。

4 つの異なる周波数帯域の平均周波数を推定することによって周波数ピークの位置を特定します。

f = [meanfreq(tones,Fs,[700 800]), ...
     meanfreq(tones,Fs,[800 900]), ...
     meanfreq(tones,Fs,[900 1000]), ...
     meanfreq(tones,Fs,[1300 1400])];
round(f)

ans = 1×4

         770         852         941        1336

推定された周波数を電話パッドの図と突き合わせると、ダイヤルされた番号は "5"、"8"、および "0" であることがわかります。ただし、周波数領域プロットではダイヤルされた順番を特定できるような時間情報は示されません。可能な組み合わせは "580"、"508"、"805"、"850"、"085"、または "058" です。このパズルを解くため、関数 pspectrum を使用して、スペクトログラムを計算し、信号の周波数成分が時間と共にどのように変化しているかを観察します。

650 ～ 1500 Hz 帯域のスペクトログラムを計算し、$-$10 dB パワー レベルに満たない成分を削除して、主な周波数成分のみを可視化します。トーンの持続時間と時間領域におけるそれらの位置を表示するには、0% のオーバーラップを使用します。

pspectrum(tones,Fs,"spectrogram",Leakage=1,OverlapPercent=0, ...
    MinThreshold=-10,FrequencyLimits=[650, 1500]);

スペクトログラムの色は、周波数のパワー レベルを符号化しています。黄色は高いパワーの周波数成分を示し、青色は非常に低いパワーの周波数成分を示します。濃い黄色の水平線は、特定の周波数のトーンが存在することを示します。プロットにはダイヤルされた 3 つの数字すべてに 1336 Hz のトーンが存在することが明確に示されており、そこからすべての数字がキーパッドの 2 列目にあることがわかります。最も低い周波数 770 Hz が最初にダイヤルされたことがプロットからわかります。次は最も高い周波数 941 Hz です。中間の周波数 852 Hz が最後です。したがって、ダイヤルされた番号は 508 となります。

最良の信号表現を得るための時間と周波数分解能のトレードオフ

関数 pspectrum は信号をセグメントに分割します。セグメントが長いほど周波数分解能が向上し、短いほど時間分解能が向上します。セグメントの長さは、FrequencyResolution と TimeResolution のパラメーターを使用して制御することができます。周波数分解能または時間分解能の値が指定されていないと、pspectrum は入力信号長に基づいて時間分解能と周波数分解能の間で適切なバランスを検出しようとします。

太平洋のシロナガスクジラの歌のふるえ声の部分を構成する、4 kHz でサンプリングされた次の信号について考えてみます。

load whaleTrill
p = audioplayer(whaleTrill,Fs,16);
play(p)

ふるえ声の信号はトーン パルスの列で構成されます。分解能が指定されていない場合と時間分解能が 10 ミリ秒に設定されている場合に、pspectrum によって取得される時間信号とスペクトログラムを確認します。Leakage パラメーターを 1 に設定して、箱型ウィンドウを使用します。パルスの時間位置を決定するため、オーバーラップ率を 0 に設定します。最後に、$-$60 dB の MinThreshold を使用して、スペクトログラム ビューからバックグラウンド ノイズを削除します。

t = (0:length(whaleTrill)-1)/Fs;
figure
ax1 = subplot(3,1,1);
plot(t,whaleTrill)
ax2 = subplot(3,1,2);
pspectrum(whaleTrill,Fs,"spectrogram",OverlapPercent=0, ...
    Leakage=1,MinThreshold=-60)
colorbar(ax2,"off")
ax3 = subplot(3,1,3);
pspectrum(whaleTrill,Fs,"spectrogram",OverlapPercent=0, ...
    Leakage=1,MinThreshold=-60,TimeResolution=10e-3)
colorbar(ax3,"off")
linkaxes([ax1,ax2,ax3],"x")

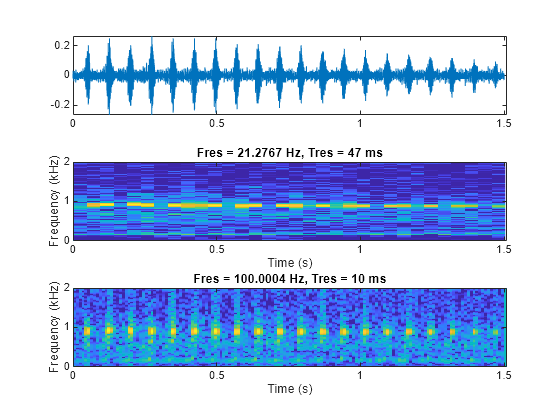
pspectrum によって選択された 47 ミリ秒の時間分解能は、スペクトログラムのすべてのふるえ声パルスの位置を決定するには大きい値です。一方、10 ミリ秒の時間分解能は時間領域での各ふるえ声パルスの位置を決定するのに十分です。これによって、少数のパルスにズームする場合でもより明確になります。

xlim([0.3 0.55])

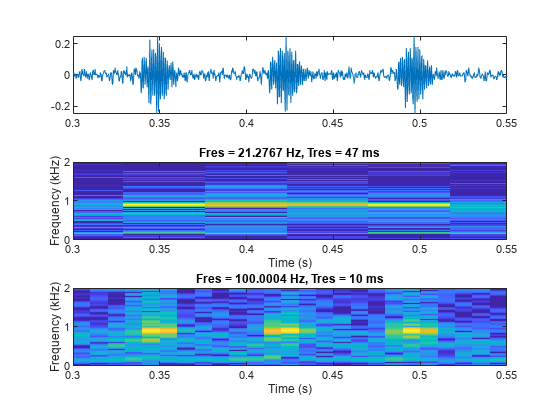
ここで、オオクビワコウモリ ("Eptesicus fuscus") の発する反響定位パルスで構成される信号を読み込みます。信号は、7 マイクロ秒のサンプリング間隔で測定されます。信号のスペクトログラムを解析します。

load batsignal
Fs = 1/DT;
figure
pspectrum(batsignal,Fs,"spectrogram")

既定のパラメーター値を使用するスペクトログラムでは、4 つの大まかな時間-周波数リッジが表示されます。周波数分解能値を 3 kHz に減らし、各リッジの周波数変動での詳細を取得します。

pspectrum(batsignal,Fs,"spectrogram",FrequencyResolution=3e3)

周波数リッジの周波数での位置決めが改善していることを確認します。ただし、周波数と時間の分解能が反比例するため、スペクトログラムの時間分解能は大幅に小さくなります。オーバーラップを 99% に設定して、時間枠を滑らかにします。$-$60 dB の MinThreshold を使用して、不要なバックグラウンド成分を削除します。

pspectrum(batsignal,Fs,"spectrogram",FrequencyResolution=3e3, ...
    OverlapPercent=99,MinTHreshold=-60)

新しい設定では、反響定位信号の 4 つの周波数リッジを明確に示すスペクトログラムが得られます。

時間-周波数の再割り当て

4 つの周波数リッジを特定できても、各リッジはまだ複数の隣接する周波数ビンに広がっていることがわかります。これは、時間と周波数の両方で使用されたウィンドウ処理法の漏れが原因です。

pspectrum関数は、時間と周波数の両方において各スペクトル推定のエネルギーの中心を推定することができます。各推定値のエネルギーを、この新しい時間および周波数の中心に最も近いビンに再度割り当てると、ウィンドウの漏れの一部を補正できます。Reassign パラメーターを使用して、これを行うことができます。このパラメーターを true に設定すると、再代入された信号のスペクトログラムを計算します。

pspectrum(batsignal,Fs,"spectrogram",FrequencyResolution=3e3, ...
    OverlapPercent=99,MinTHreshold=-60,Reassign=true)

周波数リッジは、さらにシャープになり、時間領域での位置決めが改善されました。関数 fsst を使用して、信号エネルギーの位置を求めることもできます。これについては次の節で説明します。

時間-周波数リッジの再構成

周波数が時間とともに減少するチャープ信号と最後のスプラット音で構成されている、次の音声記録について考えます。

load splat
p = audioplayer(y,Fs,16);
play(p)
pspectrum(y,Fs,"spectrogram")

時間-周波数平面でリッジを抽出することで "スプラット" 音の一部を再構成してみましょう。fsstを使用して、ノイズが含まれるスプラット信号のスペクトルをシャープにし、tfridgeを使用してチャープ音のリッジを識別し、ifsstを使用してチャープを再構成します。この処理で再構成後の信号のノイズが除去されます。

ガウス ノイズを "スプラット" 音のチャープ部分に追加します。追加されたノイズにより、安いマイクによって収録したオーディオ録音をシミュレートします。時間-周波数のスペクトル成分を確認します。

rng("default")
t = (0:length(y)-1)/Fs;
yNoise = y + 0.1*randn(size(y));
yChirp = yNoise(t<0.35);
pspectrum(yChirp,Fs,"spectrogram",MinThreshold=-70)

フーリエ シンクロスクイーズド変換 fsst を使用してスペクトルをシャープにします。fsst 関数は、固定時間の周波数のエネルギーを再代入することで、時間-周波数平面でエネルギーの位置を求めます。ノイズを含むチャープのシンクロスクイーズド変換を計算し、プロットします。

fsst(yChirp,Fs,"yaxis")

チャープは時間-周波数平面で位置決めされたリッジとして表示されます。tfridge を使用してリッジを識別します。変換と共にリッジをプロットします。

[sst,f] = fsst(yChirp,Fs); 
[fridge, iridge] = tfridge(sst,f,10);
helperPlotRidge(yChirp,Fs,fridge);

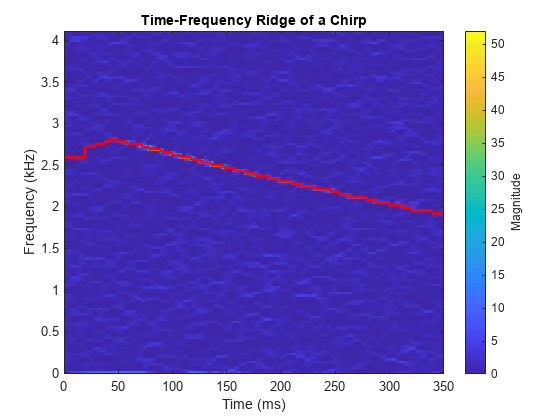
次に、リッジ インデックス ベクトル iridge を使用してチャープ信号を再構成します。リッジの両側にビンを 1 つずつ含めます。再構成後の信号のスペクトログラムをプロットします。

yrec = ifsst(sst,kaiser(256,10),iridge,NumFrequencyBins=1);
pspectrum(yrec,Fs,"spectrogram",MinThreshold=-70)

リッジの再構成により、信号からノイズが除去されています。ノイズを含む信号とノイズ除去後の信号を連続して再生し、違いを聞き比べます。

p = audioplayer([yChirp;zeros(size(yChirp));yrec],Fs,16);
play(p);

パワーの測定

複素線形周波数変調 (LFM) パルスについて考えます。これは一般的なレーダー波形です。1.27 マイクロ秒の時間分解能と 90% のオーバーラップを使用して信号のスペクトログラムを計算します。

Fs = 1e8;
bw = 60e6;
t = 0:1/Fs:10e-6;
IComp = chirp(t,-bw/2,t(end), bw/2,"linear",90)+0.15*randn(size(t));
QComp = chirp(t,-bw/2,t(end), bw/2,"linear",0) +0.15*randn(size(t));
IQData = IComp + 1i*QComp;

segmentLength = 128;
pspectrum(IQData,Fs,"spectrogram",TimeResolution=1.27e-6,OverlapPercent=90)

スペクトログラムの計算に使用されるパラメーターは、LFM 信号の時間-周波数表現を明確にします。pspectrum はパワー スペクトログラムを計算します。これは、カラー値が dB 単位の真のパワー レベルに対応することを意味します。カラー バーは、信号のパワー レベルが約 $-$4 dB であることを示します。

対数周波数スケールによる可視化

特定の用途では、信号のスペクトログラムが対数周波数スケール上に可視化されている方が望ましい場合もあります。これを行うには、y 軸の YScale プロパティを変更します。たとえば、1 kHz でサンプリングされた対数チャープについて考えます。チャープの周波数は 10 秒間で 10 Hz から 400 Hz に増加します。

Fs = 1e3;                    
t = 0:1/Fs:10;               
fo = 10;                     
f1 = 400;                    
y = chirp(t,fo,10,f1,"logarithmic");
pspectrum(y,Fs,"spectrogram",FrequencyResolution=1, ...
    OverlapPercent=90,Leakage=0.85,FrequencyLimits=[1 Fs/2])

このチャープのスペクトログラムは、周波数スケールが対数のときに直線になります。

ax = gca;
ax.YScale = "log";

3 次元ウォーターフォールによる可視化

view コマンドを使用すると、信号のスペクトログラムを 3 次元ウォーターフォール プロットとして可視化できます。関数 colormap によって表示色を変えることもできます。

Fs = 10e3;
t = 0:1/Fs:2;
x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*Fs,Fs);
pspectrum(x1,Fs,"spectrogram",Leakage=0.8)

view(-45,65)
colormap bone

パーシステンス スペクトルを使用した干渉の検出

信号のパーシステンス スペクトルは、与えられた周波数が信号内に存在する時間の割合を示す時間-周波数領域のビューです。パーシステンス スペクトルはパワー周波数空間のヒストグラムです。信号が変化する中で特定の周波数が信号内に存在する時間が長ければ長いほど、その時間の割合は大きくなるため、表示内の色が明るく ("熱く") なります。パーシステンス スペクトルを使用して、他の信号の中に隠れている信号を識別します。

広帯域信号に組み込まれた狭帯域の干渉信号を考えてみます。1 kHz で 500 秒間サンプリングされたチャープを生成します。チャープの周波数は、測定中に 180 Hz から 220 Hz に増加します。

fs = 1000;
t = (0:1/fs:500)';

x = chirp(t,180,t(end),220) + 0.15*randn(size(t));

信号には振幅が 0.05 の 210 Hz 干渉が含まれます。これは、信号の合計持続時間の 1/6 のみに存在します。

idx = floor(length(x)/6);
x(1:idx) = x(1:idx) + 0.05*cos(2*pi*t(1:idx)*210);

区間 100 ～ 290 Hz の信号のパワー スペクトルを計算します。弱い正弦波はチャープによって不明瞭になります。

pspectrum(x,fs,FrequencyLimits=[100 290])

信号のパーシステンス スペクトルを計算します。今度は、両方の信号成分が明瞭に表示されます。

figure
colormap parula
pspectrum(x,fs,"persistence",FrequencyLimits=[100 290],TimeResolution=1)

まとめ

この例では、pspectrum関数を使用して時間-周波数解析を行う方法とスペクトログラム データとパワー レベルを解釈する方法を説明しました。また、信号の理解を高めるために時間と周波数の分解能を変更する方法と fsst、ifsst、および tfridge を使用して、スペクトルをシャープにし、時間-周波数リッジを抽出する方法について説明しました。対数周波数スケールおよび 3 次元可視化を使用するためのスペクトログラム プロットの設定方法を説明しました。最後に、パーシステンス スペクトルを計算して、干渉信号を検出する方法を説明しました。

付録

この例では次の補助関数が使用されています。