このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
stftmag2sig
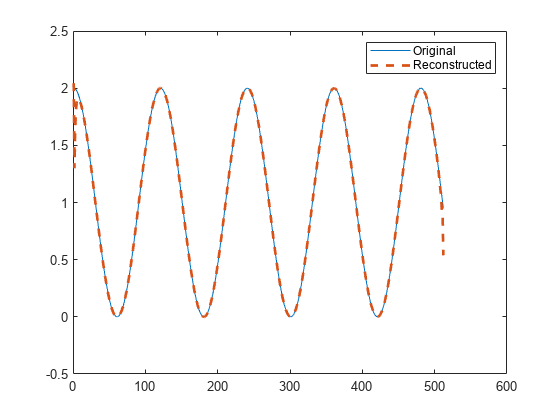
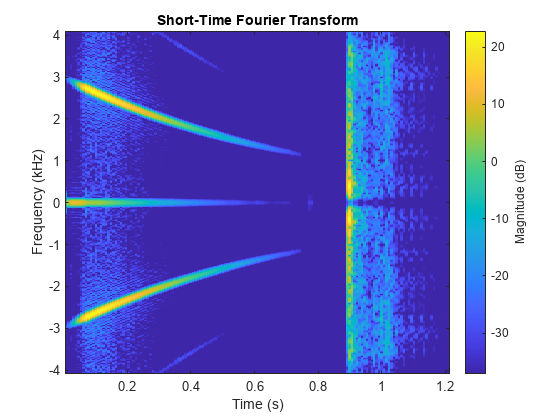
STFT 振幅からの信号の再構成
構文
説明
x = stftmag2sig(___,Name=Value)FrequencyRange="onesided",InitializePhaseMethod="random" は、ランダムな初期位相の片側 STFT から信号が再構成されることを指定します。
例
正規化周波数が ラジアン/サンプル、DC 値が 1 の正弦波サンプル 512 個について考えます。信号の STFT を計算します。
n = 512; x = cos(pi/60*(0:n-1)')+1; S = stft(x);
STFT の振幅から正弦波を再構成します。元の信号と再構成後の信号をプロットします。
xr = stftmag2sig(abs(S),size(S,1)); plot(x) hold on plot(xr,"--",LineWidth=2) hold off legend("Original","Reconstructed")
計算を繰り返しますが、今回は信号をゼロでパディングして、エッジの影響を減らします。
xz = circshift([x; zeros(n,1)],n/2); Sz = stft(xz); xr = stftmag2sig(abs(Sz),size(Sz,1)); xz = xz(n/2+(1:n)); xr = xr(n/2+(1:n)); plot(xz) hold on plot(xr,"--",LineWidth=2) hold off legend("Original","Reconstructed")
計算を繰り返しますが、今回は x を、長さが 2 倍の信号のセグメントだと仮定して、エッジの影響を減らします。
xx = cos(pi/60*(-n/2:n/2+n-1)')+1; Sx = stft(xx); xr = stftmag2sig(abs(Sx),size(Sx,1)); xx = xx(n/2+(1:n)); xr = xr(n/2+(1:n)); plot(xx) hold on plot(xr,"--",LineWidth=2) hold off legend("Original","Reconstructed")
減少する 2 つのチャープと広帯域のスプラッター音を含むオーディオ信号を読み込みます。信号は 8192 Hz でサンプリングされています。信号の STFT をプロットします。波形を 128 サンプルのセグメントに分割し、ハミング ウィンドウを使用してセグメントにウィンドウを適用します。隣り合ったセグメント間のオーバーラップを 64 サンプル、DFT 点を 1024 に指定します。
load splat ty = (0:length(y)-1)/Fs; % To hear, type sound(y,Fs) wind = hamming(128); olen = 64; nfft = 1024; stft(y,Fs,Window=wind,OverlapLength=olen,FFTLength=nfft)
STFT の振幅と位相を計算します。
s = stft(y,Fs,Window=wind,OverlapLength=olen,FFTLength=nfft); smag = abs(s); sphs = angle(s);
STFT の振幅に基づいて信号を再構成します。STFT を計算したときと同じパラメーターを使用します。既定では、stftmag2sig は、位相をゼロに初期化し、100 回の最適化反復を使用します。
[x,tx,info] = stftmag2sig(smag,nfft,Fs, ... Window=wind,OverlapLength=olen); % To hear the reconstruction, type sound(x,Fs)
元の信号と再構成後の信号をプロットします。より良く比較するために、再構成された信号を垂直方向と右方向にシフトします。
plot(ty,y,tx+500/Fs,x+1) legend("Original","Reconstructed",Location="best")
最後の 2 つの繰り返し間の収束に向けた相対的改善を出力します。
impr = info.Inconsistency
impr = 0.0579
最適化反復の数を 2 倍にし、初期位相を STFT から実際の位相に設定して、再構成を改善します。元の信号と再構成後の信号をプロットします。より良く比較するために、再構成された信号の負の値をプロットし、それを垂直方向と右方向にシフトします。
[x,tx,info] = stftmag2sig(smag,nfft,Fs, ... Window=wind,OverlapLength=olen, ... MaxIterations=200,InitialPhase=sphs); % To hear the reconstruction, type sound(x,Fs) plot(ty,y,tx+500/Fs,-x+1) legend("Original","Reconstructed",Location="best")
最後の 2 つの繰り返し間の収束に向けた相対的改善を出力します。
impr = info.Inconsistency
impr = 2.0848e-16
5 kHz で 4 秒間サンプリングされた信号を生成します。信号は、振動する振幅の領域および増加トレンドで変動する周波数の領域によって分離された、持続時間が減少していく一連のパルスで構成されています。
fs = 5000; t = 0:1/fs:4-1/fs; x = 10*besselj(0,1000*(sin(2*pi*(t+2).^3/60).^5));
信号の短時間フーリエ変換を計算してプロットします。信号を 128 サンプルのセグメントに分割し、ハン ウィンドウを使用してセグメントをウィンドウ処理します。隣り合ったセグメント間のオーバーラップを 96 サンプル、DFT 点を 128 に指定します。
win = hann(128); olen = 96; nfft = 128; stft(x,fs,Window=win,OverlapLength=olen,FFTLength=nfft)
STFT の振幅と位相を計算します。
s = stft(x,fs,Window=win,OverlapLength=olen,FFTLength=nfft); smag = abs(s); sphs = angle(s);
STFT の振幅に基づいて信号を再構成します。STFT を計算したときと同じパラメーターを使用します。既定の Griffin-Lim アルゴリズムを使用する代わりに、ADAM オプティマイザーで勾配降下法を使用します。
[xrec,trec,info] = stftmag2sig(smag,nfft,fs, ... Window=win,Method="gd",Optimizer="adam");
元の信号と再構成後の信号をプロットします。より良く比較するために、再構成された信号を垂直方向にシフトして、両方が表示されるようにします。
plot(t,x,trec,xrec+12) legend("Original","Reconstructed",Location="northwest") ylim([-5 27])
元の信号と再構成信号の間の平均二乗誤差を計算します。
sum((x-xrec').^2)/length(x)
ans = 1.3620
再現性を得るために、乱数シードを既定値に設定します。2 チャネル正弦波の 160 サンプルを生成します。各チャネルにノイズを付加します。
最初のチャネルは、単位振幅および ラジアン/サンプルの正規化された正弦波周波数をもちます。
2 番目のチャネルは、単位振幅および ラジアン/サンプルの正規化された正弦波周波数をもちます。
信号の STFT を計算します。信号を 32 サンプルのセグメントに分割し、ハン ウィンドウを使用してセグメントをウィンドウ処理します。
rng default
N = 160;
t = 0:N-1;
win = hann(32);
signal = cos(pi./[4;2]*t)'+randn(N,2)/5;
s = stft(signal,Window=win);STFT の振幅から信号を再構成します。L-BFGS オプティマイザーで勾配降下法を使用します。L-BFGS オプティマイザーは、各反復のステップ サイズを自動的に選択します。最適化プロセス中の各チャネルの正規化された不整合を追跡します。
[x,tx,info] = stftmag2sig(abs(s), ... size(s,1),Window=win, ... Method="gd",Optimizer="lbfgs", ... Display=true);
#Iteration | Normalized Inconsistency
1 | 1.2078e+00 1.2042e+00
20 | 3.2348e-02 9.6221e-03
40 | 1.9969e-02 6.8350e-03
60 | 2.5463e-03 1.2099e-03
80 | 2.4790e-03 8.4016e-04
100 | 5.4774e-03 7.1804e-04
Decomposition process stopped.
The number of iterations reached the specified "MaxIterations" value of 100.
元の信号と再構成後の信号をプロットします。
tiledlayout(2,1) nexttile plot(t,signal(:,1)) hold on plot(tx,x(:,1),"--",LineWidth=2) hold off title("First Channel") legend("Original","Reconstructed", ... Location="northoutside") nexttile plot(t,signal(:,2)) hold on plot(tx,x(:,2),"--",LineWidth=2) hold off title("Second Channel")
最後の 2 つの繰り返し間の収束に向けた相対的改善を出力します。
info.Inconsistency
ans = 1×2
0.0055 0.0007
入力引数
名前と値の引数
出力引数
詳細
ヒント
参照
[1] Griffin, Daniel W., and Jae S. Lim. "Signal Estimation from Modified Short-Time Fourier Transform." IEEE Transactions on Acoustics, Speech, and Signal Processing. Vol. 32, Number 2, April 1984, pp. 236–243. https://doi.org/10.1109/TASSP.1984.1164317.
[2] Perraudin, Nathanaël, Peter Balazs, and Peter L. Søndergaard. "A Fast Griffin-Lim Algorithm." In 2013 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, October 20–23, 2013. https://doi.org/10.1109/WASPAA.2013.6701851.
[3] Le Roux, Jonathan, Hirokazu Kameoka, Nobutaka Ono, and Shigeki Sagayama. "Fast Signal Reconstruction from Magnitude STFT Spectrogram Based on Spectrogram Consistency." In Proceedings of the 13th International Conference on Digital Audio Effects (DAFx-10), Graz, Austria, September 6–10, 2010.
[4] Ji, Li, and Zhou Tie. “On Gradient Descent Algorithm for Generalized Phase Retrieval Problem.” In 2016 IEEE 13th International Conference on Signal Processing (ICSP), 320–25. Chengdu, China: IEEE, 2016. https://doi.org/10.1109/ICSP.2016.7877848.
