幾何学的変換の行列表現

線形幾何学的変換は数値行列として表すことができます。平行移動、スケーリング、回転、反転などの変換の各種類は、要素が特定のパターンに従う行列を使用して定義されます。変換を表す行列の合成を取ることにより、複数の変換を組み合わせることができます。詳細については、Create Composite 2-D Affine Transformationsを参照してください。

2 次元アフィン変換

この表は、2 次元アフィン変換と、各アフィン変換の定義に使用する変換行列をまとめています。2 次元アフィン変換の場合は、最後の行が [0 0 1] でなければなりません。

• 2 次元の平行移動行列の組み合わせを使用して、平行移動変換を表す transltform2d オブジェクトを作成します。

• 2 次元の平行移動行列と回転行列の組み合わせを使用して、無反射剛体変換を表す rigidtform2d オブジェクトを作成します。

• 2 次元の平行移動行列、回転行列、スケーリング行列の組み合わせを使用して、無反射相似変換を表す simtform2d オブジェクトを作成します。

• 任意の組み合わせの 2 次元変換行列を使用して、一般的なアフィン変換を表す affinetform2d オブジェクトを作成します。

2 次元アフィン変換	例 (元のイメージと変換されたイメージ)	変換行列
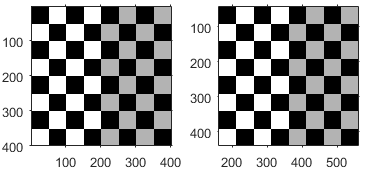
平行移動		$$\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]$$	tx は "x" 軸に沿って移動を指定します。 ty は "y" 軸に沿って移動を指定します。 ピクセル座標の詳細については、イメージの座標系を参照してください。
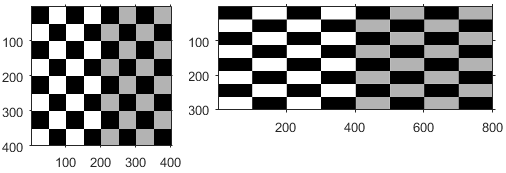
スケール		$$\left[\begin{array}{ccc}{s}_x& 0& 0\\ 0& s_y& 0\\ 0& 0& 1\end{array}\right]$$	sx は "x" 軸に沿って倍率を指定します。 sy は "y" 軸に沿って倍率を指定します。
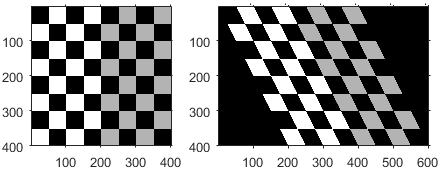
せん断		$$\left[\begin{array}{ccc}1& s{h}_x& 0\\ s{h}_y& 1& 0\\ 0& 0& 1\end{array}\right]$$	shx は "x" 軸に沿ってせん断係数を指定します。 shy は "y" 軸に沿ってせん断係数を指定します。
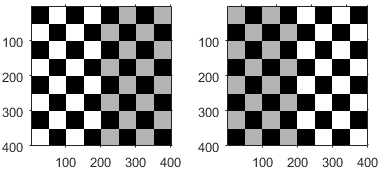
反転		$$\left[\begin{array}{ccc}\text{cosd(2}\phi \text{)}& \text{sind(2}\phi \text{)}& 0\\ \text{sind(2}\phi \text{)}& -\text{cosd(2}\phi \text{)}& 0\\ 0& 0& 1\end{array}\right]$$	φ は、反転の軸の角度 (度数) を指定します。 よく使われる反転は、垂直方向の反転と水平方向の反転の 2 つです。垂直方向の反転は、x 軸を中心とする反転です。このため、φ は 0 であり、反転行列は以下のように単純化されます。 [1 0 0; 0 -1 0; 0 0 1]. 水平方向の反転は、y 軸を中心とする反転です。このため、φ は 90 であり、反転行列は以下のように単純化されます。 [-1 0 0; 0 1 0; 0 0 1]
回転		$$\left[\begin{array}{ccc}\mathrm{cosd}(\text{θ})& -\mathrm{sind}(\text{θ})& 0\\ \mathrm{sind}(\text{θ})& \mathrm{cosd}(\text{θ})& 0\\ 0& 0& 1\end{array}\right]$$	θ は原点を中心とする回転の角度 (度数) を指定します。

2 次元射影変換

射影変換ではイメージの平面を傾けることができます。平行線は消失点に向かって収束し、奥行があるように見えます。

変換は 3 行 3 列の行列です。アフィン変換とは異なり、変換行列の最後の行に制約はありません。2 次元のアフィン変換行列と射影変換行列の任意の合成を使用して、一般的な射影変換を表す projtform2d オブジェクトを作成します。

2 次元射影変換	例	変換行列
傾き		$$\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ E& F& 1\end{array}\right]$$	E および F は消失点に影響を与えます。 E と F を大きくすると、消失点が原点に近くなるため、平行線がより速く収束するように見えます。

3 次元アフィン変換

この表は、3 次元アフィン変換と、各アフィン変換の定義に使用する変換行列をまとめています。3 次元の場合は、イメージの回転方法またはせん断方法に応じて複数の行列があります。3 次元アフィン変換の場合は、最後の行が [0 0 0 1] でなければなりません。

• 3 次元の平行移動行列の組み合わせを使用して、平行移動変換を表す transltform3d オブジェクトを作成します。

• 3 次元の平行移動行列と回転行列の組み合わせを使用して、無反射剛体変換を表す rigidtform3d オブジェクトを作成します。

• 3 次元の平行移動行列、回転行列、スケーリング行列の組み合わせを使用して、無反射相似変換を表す simtform3d オブジェクトを作成します。

• 任意の組み合わせの 3 次元変換行列を使用して、一般的なアフィン変換を表す affinetform3d オブジェクトを作成します。

3 次元アフィン変換	変換行列
平行移動	x、y、z の方向に、それぞれ tx、ty、tz の量での平行移動 $$\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]$$
スケール	x、y、z の方向に、それぞれ sx、sy、sz の倍率でのスケーリング $$\left[\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 1\end{array}\right]$$
せん断	y-z 平面内でのせん断 $$\left[\begin{array}{cccc}1& 0& 0& 0\\ s{h}_{xy}& 1& 0& 0\\ s{h}_{xz}& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$ 条件 $$\begin{array}{l}x\text{'}=x\\ y\text{'}=y+s{h}_{xy}x\\ z\text{'}=z+s{h}_{xz}x\end{array}$$	x-z 平面内でのせん断 $$\left[\begin{array}{cccc}1& s{h}_{yx}& 0& 0\\ 0& 1& 0& 0\\ 0& s{h}_{yz}& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$ 条件 $$\begin{array}{l}x\text{'}=x+s{h}_{yx}y\\ y\text{'}=y\\ z\text{'}=z+s{h}_{yz}y\end{array}$$	x-y 平面内でのせん断 $$\left[\begin{array}{cccc}1& 0& s{h}_{zx}& 0\\ 0& 1& s{h}_{zy}& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$ 条件 $$\begin{array}{l}x\text{'}=x+s{h}_{zx}z\\ y\text{'}=y+s{h}_{zy}z\\ z\text{'}=z\end{array}$$
反転	y-z 平面上での x 座標の符号反転による反転 $$\left[\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$	x-z 平面上での y 座標の符号反転による反転 $$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$	x-y 平面上での z 座標の符号反転による反転 $$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& 1\end{array}\right]$$
回転	y-z 平面内での x 軸を中心とした角度 θx (度数) の回転 $$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \text{cosd}({\theta }_x)& -\text{sind}({\theta }_x)& 0\\ 0& \text{sind}({\theta }_x)& \text{cosd}({\theta }_x)& 0\\ 0& 0& 0& 1\end{array}\right]$$	x-z 平面内での y 軸を中心とした角度 θy (度数) の回転 $$\left[\begin{array}{cccc}\text{cosd}({\theta }_y)& 0& \text{sind}({\theta }_y)& 0\\ 0& 1& 0& 0\\ -\mathrm{sind}({\theta }_y)& 0& \text{cosd}({\theta }_y)& 0\\ 0& 0& 0& 1\end{array}\right]$$	x-y 平面内での z 軸を中心とした角度 θz (度数) の回転 $$\left[\begin{array}{cccc}\text{cosd}({\theta }_z)& -\text{sind}({\theta }_z)& 0& 0\\ \text{sind}({\theta }_z)& \text{cosd}({\theta }_z)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

3 次元射影変換と N 次元変換

関数 imwarp は、3 次元射影変換、または N 次元アフィンおよび射影変換をサポートしていません。その代わりに、関数 maketform を使用して幾何学的変換行列から空間変換構造体を作成できます。作成後、関数 tformarray を使用してその変換をイメージに適用します。詳細については、N 次元空間変換を参照してください。

変換行列の次元は、(N+1) 行 (N+1) 列でなければなりません。関数 maketform および tformarray は、右から乗算する行列規則を使用します。右から乗算する規則の幾何学的変換行列は、左から乗算する規則の行列の転置です。このため、N 次元アフィン変換行列の場合、最後の列は [zeros(N,1); 1] を含まなければなりません。最後の行の値には制約がありません。

参考

imwarp | fitgeotform2d | affinetform2d | affinetform3d | projtform2d

関連する例

• Create Composite 2-D Affine Transformations
• シンプルな 2 次元平行移動変換の実行

詳細

• 2 次元および 3 次元の幾何学的変換プロセスの概要