シンプルな 2 次元平行移動変換の実行
この例では、平行移動と呼ばれる単純なアフィン変換を実行する方法を示します。平行移動では、指定した値を x 座標と y 座標に加えて座標空間でイメージを移動します。(また、関数 imtranslate を使用して平行移動を実行することもできます)。
変換するイメージを読み取ります。この例では、関数 checkerboard を使用してチェッカーボードのイメージを作成します。
cb = checkerboard; imshow(cb)

イメージに関する空間参照情報を取得します。この情報は変換の結果を表示する場合に役立ちます。
cb_ref = imref2d(size(cb))
cb_ref =
imref2d with properties:
XWorldLimits: [0.5000 80.5000]
YWorldLimits: [0.5000 80.5000]
ImageSize: [80 80]
PixelExtentInWorldX: 1
PixelExtentInWorldY: 1
ImageExtentInWorldX: 80
ImageExtentInWorldY: 80
XIntrinsicLimits: [0.5000 80.5000]
YIntrinsicLimits: [0.5000 80.5000]
"x" 方向および "y" 方向における平行移動の量を指定します。
tx = 20; ty = 30;
平行移動変換を表す transltform2d 幾何学的変換オブジェクトを作成します。他のタイプの幾何学的変換の場合は、他のタイプのオブジェクトを使用します。
tform = transltform2d(tx,ty);
変換を実行します。関数 imwarp を呼び出し、変換するイメージと幾何学的変換オブジェクトを指定します。imwarp は変換されたイメージ cb_translated を返します。また、この例では、オプションの空間参照オブジェクト cb_translated_ref も返されます。これには変換されたイメージの空間参照情報が含まれています。
[cb_translated,cb_translated_ref] = imwarp(cb,tform);
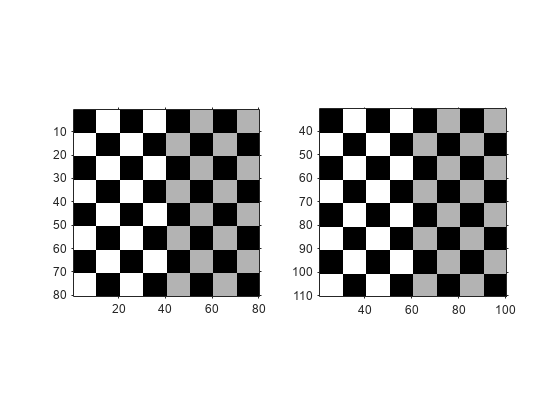
元のイメージと変換後のイメージを並べて表示します。平行移動後のイメージを表示すると、変換では何も行われなかったように見えるかもしれません。変換したイメージが元のイメージと同じに見えます。可視化に変化が見受けられない理由は、出力座標空間全体が表示されるのではなく、変換したイメージ全体がちょうど含まれる大きさに imwarp が出力イメージのサイズを調整するからです。ただし、変換によって座標の値が変化していることに注目してください。
figure subplot(1,2,1) imshow(cb,cb_ref) subplot(1,2,2) imshow(cb_translated,cb_translated_ref)
変換したイメージ全体を元のイメージと同じ座標空間の原点に対する位置関係で表示するには、imwarp で名前と値の引数 "OutputView" を使用し、空間参照オブジェクトを指定します。空間参照オブジェクトは、出力イメージのサイズと出力イメージに含める出力座標空間のサイズを指定します。これを行うため、この例では元のイメージに関連付けられている空間参照オブジェクトのコピーを作成し、変換したイメージ全体が収まるようにワールド座標の範囲を変更します。この例では、入力イメージの原点が表示されるように、ワールド座標で出力イメージの範囲を設定しています。
cb_translated_ref = cb_ref;
cb_translated_ref.XWorldLimits(2) = cb_translated_ref.XWorldLimits(2)+tx;
cb_translated_ref.YWorldLimits(2) = cb_translated_ref.YWorldLimits(2)+ty;
[cb_translated,cb_translated_ref] = imwarp(cb,tform, ...
OutputView=cb_translated_ref);
figure
subplot(1,2,1)
imshow(cb,cb_ref)
subplot(1,2,2)
imshow(cb_translated,cb_translated_ref);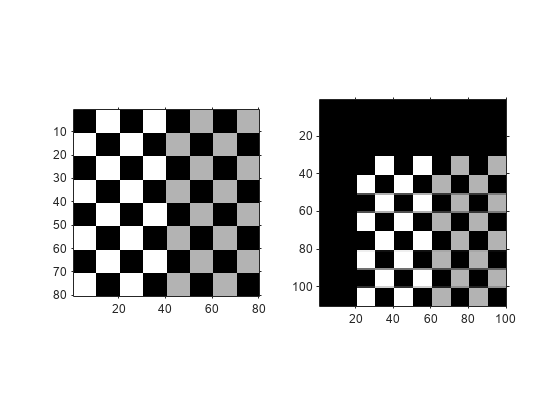
参考
imwarp | imref2d | transltform2d | affinetform2d