Main Content

isminphase

Verify that discrete-time filter System object is minimum phase

collapse all in page

Syntax

flag = isminphase(sysobj)
flag = isminphase(sysobj,tol)
flag = isminphase(___,Arithmetic=arithType)

Description

flag = isminphase(sysobj) returns true if the filter System object™ has minimum phase.

example

flag = isminphase(sysobj,tol) uses the tolerance tol to determine when two numbers are close enough to be considered equal. If not specified, tol defaults to eps^(2/3).

flag = isminphase(___,Arithmetic=arithType) analyzes the filter System object based on the arithmetic specified in the arithType input using either of the previous syntaxes.

For more input options, see isminphase in Signal Processing Toolbox™.

Examples

collapse all

Open Live Script

Design a Chebyshev Type I IIR filter and determine if the filter has minimum phase and is stable.

Using the fdesign.lowpass and design functions, design a Chebyshev Type I IIR filter with a passband ripple of 0.5 dB and a 3 dB cutoff frequency at 9600 Hz. 

Fs = 48000; % Sampling frequency of input signal
d  = fdesign.lowpass('N,F3dB,Ap', 10, 9600, .5, Fs);
filt = design(d,'cheby1',Systemobject=true)
filt = 
  dsp.SOSFilter with properties:

            Structure: 'Direct form II'
    CoefficientSource: 'Property'
            Numerator: [5x3 double]
          Denominator: [5x3 double]
       HasScaleValues: true
          ScaleValues: [0.3318 0.2750 0.1876 0.0904 0.0225 0.9441]

  Use get to show all properties

Using the isminphase function, determine if the filter has minimum phase.

isminphase(filt)
ans = logical
   1

Verify the location of poles and zeros of the filter transfer function on the z-plane. By definition, the poles and zeros of the minimum phase filter must be on or inside the unit circle.

zplane(filt)

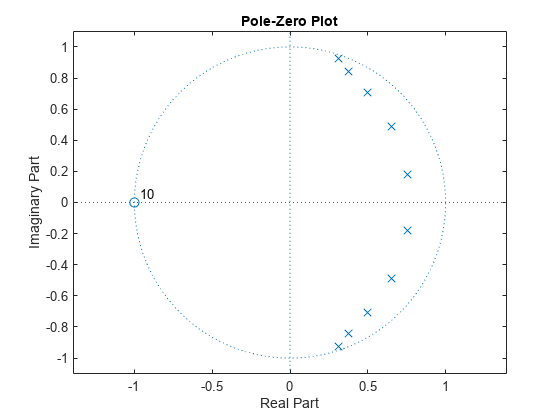
Figure contains an axes object. The axes object with title Pole-Zero Plot, xlabel Real Part, ylabel Imaginary Part contains 4 objects of type line, text. One or more of the lines displays its values using only markers

All minimum phase filters are stable. To verify if the designed filter is stable, use the isstable function.

isstable(filt)
ans = logical
   1

Input Arguments

collapse all

Tolerance value to determine when two numbers are close enough to be considered equal, specified as a positive scalar. If not specified, tol defaults to eps^(2/3).

Arithmetic used in the filter analysis, specified as 'double', 'single', or 'Fixed'. When the arithmetic input is not specified and the filter System object is unlocked, the analysis tool assumes a double-precision filter. When the arithmetic input is not specified and the System object is locked, the function performs the analysis based on the data type of the locked input.

The 'Fixed' value applies to filter System objects with fixed-point properties only.

When the 'Arithmetic' input argument is specified as 'Fixed' and the filter object has the data type of the coefficients set to 'Same word length as input', the arithmetic analysis depends on whether the System object is unlocked or locked.

  • unlocked –– The analysis object function cannot determine the coefficients data type. The function assumes that the coefficients data type is signed, has a 16-bit word length, and is auto scaled. The function performs fixed-point analysis based on this assumption.

  • locked –– When the input data type is 'double' or 'single', the analysis object function cannot determine the coefficients data type. The function assumes that the data type of the coefficients is signed, has a 16-bit word length, and is auto scaled. The function performs fixed-point analysis based on this assumption.

To check if the System object is locked or unlocked, use the isLocked function.

When the arithmetic input is specified as 'Fixed' and the filter object has the data type of the coefficients set to a custom numeric type, the object function performs fixed-point analysis based on the custom numeric data type.

Output Arguments

collapse all

Flag to determine if the filter has minimum phase, returned as a logical:

  • 1 –– Filter has minimum phase.

  • 0 –– Filter has non minimum phase.

Data Types: logical

More About

collapse all

Minimum Phase Filters

A causal and stable discrete-time system is said to be strictly minimum-phase when all its zeros are inside the unit circle. A causal and stable LTI system is a minimum-phase system if its inverse is causal and stable as well.

Such a system is called a minimum-phase system because it has the minimum group delay (grpdelay) of the set of systems that have the same magnitude response.

Version History

Introduced in R2013a

expand all

See Also

|