fitrnet

ニューラルネットワーク回帰モデルの学習

ニューラルネットワーク回帰モデルに学習させ、テストセットでモデルの性能を評価します。

carbig データセットを読み込みます。このデータセットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。Acceleration、Displacement などの予測子変数と応答変数 MPG が格納された table を作成します。

load carbig
cars = table(Acceleration,Displacement,Horsepower, ...
    Model_Year,Origin,Weight,MPG);

cars から table に欠損値がある行を削除します。

cars = rmmissing(cars);

米国製かどうかに基づいて、自動車を分類します。

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan",...
    "Germany","Sweden","Italy","England"],"NotUSA");

データを学習セットとテストセットに分割します。観測値の約 80% をニューラルネットワークモデルの学習に使用し、観測値の約 20% を学習済みモデルの新しいデータでの性能のテストに使用します。cvpartition を使用してデータを分割します。

rng("default") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);
trainingIdx = training(c); % Training set indices
carsTrain = cars(trainingIdx,:);
testIdx = test(c); % Test set indices
carsTest = cars(testIdx,:);

学習データ carsTrain を関数 fitrnet に渡して、ニューラルネットワーク回帰モデルに学習させます。より良い結果を得るために、予測子データを標準化するように指定します。

Mdl = fitrnet(carsTrain,"MPG","Standardize",true)

Mdl = 
  RegressionNeuralNetwork
           PredictorNames: {'Acceleration'  'Displacement'  'Horsepower'  'Model_Year'  'Origin'  'Weight'}
             ResponseName: 'MPG'
    CategoricalPredictors: 5
        ResponseTransform: 'none'
          NumObservations: 314
               LayerSizes: 10
              Activations: 'relu'
    OutputLayerActivation: 'none'
                   Solver: 'LBFGS'
          ConvergenceInfo: [1×1 struct]
          TrainingHistory: [708×7 table]


  Properties, Methods

Mdl は学習させた RegressionNeuralNetwork モデルです。ドット表記を使用して Mdl のプロパティにアクセスできます。たとえば、Mdl.TrainingHistory と指定すると、ニューラルネットワークモデルの学習履歴についての詳細情報を取得できます。

検定の平均二乗誤差 (MSE) を計算して、テストセットで回帰モデルの性能を評価します。MSE の値が小さいほど、パフォーマンスが優れていることを示します。

testMSE = loss(Mdl,carsTest,"MPG")

testMSE = 
7.1092

全結合層の構成

ニューラルネットワークの全結合層を構成します。

carbig データセットを読み込みます。このデータセットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。予測子変数 Acceleration、Cylinders などが含まれている行列 X を作成します。応答変数 MPG を変数 Y に保存します。

load carbig
X = [Acceleration Cylinders Displacement Weight];
Y = MPG;

X および Y からいずれかの配列に欠損値がある行を削除します。

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

データを学習データ (XTrain および YTrain) とテストデータ (XTest および YTest) に分割します。観測値の約 20% を検定用に予約し、残りの観測値を学習に使用します。

rng("default") % For reproducibility of the partition
c = cvpartition(length(Y),"Holdout",0.20);
trainingIdx = training(c); % Indices for the training set
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);
testIdx = test(c); % Indices for the test set
XTest = X(testIdx,:);
YTest = Y(testIdx);

ニューラルネットワーク回帰モデルに学習させます。予測子データを標準化するように指定し、最初の全結合層の出力数を 30、2 番目の全結合層の出力数を 10 に指定します。既定では、どちらの層でも正規化線形ユニット (ReLU) 活性化関数が使用されます。全結合層の活性化関数は、名前と値の引数 Activations を使用して変更できます。

Mdl = fitrnet(XTrain,YTrain,"Standardize",true, ...
    "LayerSizes",[30 10])

Mdl = 
  RegressionNeuralNetwork
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
          NumObservations: 319
               LayerSizes: [30 10]
              Activations: 'relu'
    OutputLayerActivation: 'none'
                   Solver: 'LBFGS'
          ConvergenceInfo: [1×1 struct]
          TrainingHistory: [1000×7 table]


  Properties, Methods

Mdl の LayerWeights プロパティと LayerBiases プロパティを使用して、学習させたモデルの全結合層の重みとバイアスにアクセスします。各プロパティの最初の 2 つの要素が最初の 2 つの全結合層の値に対応し、3 番目の要素が回帰用の最終全結合層の値に対応します。たとえば、最初の全結合層の重みとバイアスを表示します。

Mdl.LayerWeights{1}

ans = 30×4

    0.0123    0.0117   -0.0094    0.1175
   -0.4081   -0.7849   -0.7201   -2.1720
    0.6041    0.1680   -2.3952    0.0934
   -3.2332   -2.8360   -1.8264   -1.5723
    0.5851    1.5370    1.4623    0.6742
   -0.2106    1.2830   -1.7489   -1.5556
    0.4800    0.1012   -1.0044   -0.7959
    1.8015   -0.5272   -0.7670    0.7496
   -1.1428   -0.9902    0.2436    1.2288
   -0.0833   -2.4265    0.8388    1.8597
    0.1069   -0.6754   -2.4190   -2.1763
   -0.4008    1.1705    2.0588    0.2282
    0.6358   -0.4830   -1.6925   -1.1925
   -0.9572   -1.2231    1.1647    1.0479
   -0.5559   -0.0917   -3.6854    1.2579
      ⋮

Mdl.LayerBiases{1}

最終全結合層の出力は 1 つです。層の出力の数は、層の重みと層のバイアスの最初の次元に対応します。

size(Mdl.LayerWeights{end})

ans = 1×2

     1    10

size(Mdl.LayerBiases{end})

ans = 1×2

     1     1

学習させたモデルの性能を推定するには、Mdl のテストセットの平均二乗誤差 (MSE) を計算します。MSE の値が小さいほど、パフォーマンスが優れていることを示します。

testMSE = loss(Mdl,XTest,YTest)

testMSE = 
18.3681

テストセットの予測応答値と実際の応答値を比較します。予測されるガロンあたりの走行マイル数 (MPG) を縦軸に、実際の MPG を横軸にしてプロットします。基準線上にある点は予測が正しいことを示します。優れたモデルでは、生成された予測が線の近くに分布します。

testPredictions = predict(Mdl,XTest);
plot(YTest,testPredictions,".")
hold on
plot(YTest,YTest)
hold off
xlabel("True MPG")
ylabel("Predicted MPG")

Figure contains an axes object. The axes object with xlabel True MPG, ylabel Predicted MPG contains 2 objects of type line. One or more of the lines displays its values using only markers

ニューラルネットワーク回帰モデルのアーキテクチャの指定

R2025a 以降

この例では次を使用します。

Deep Learning Toolbox™ を使用してカスタムのニューラルネットワークアーキテクチャを指定します。

全結合層が直列に接続されたニューラルネットワークを指定するには、LayerSizes 引数などの引数を使用してニューラルネットワークアーキテクチャを構成します。さらに複雑なアーキテクチャをもつニューラルネットワーク (スキップ接続をもつニューラルネットワークなど) の場合は、名前と値の引数 Network で dlnetwork オブジェクトを使用してアーキテクチャを指定できます。

carbig データセットを読み込みます。

load carbig
X = [Acceleration Cylinders Displacement Weight];
Y = MPG;

いずれかの配列に欠損値があるデータの行を削除します。

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

rng("default") % For reproducibility of the partition
c = cvpartition(length(Y),Holdout=0.2);
trainingIdx = training(c); % Indices for the training set
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);
testIdx = test(c); % Indices for the test set
XTest = X(testIdx,:);
YTest = Y(testIdx);

次の特性をもつニューラルネットワークアーキテクチャを定義します。

予測子の数と一致する入力サイズをもつ特徴入力層。
3 つの全結合層とそれに続く ReLU 層が直列に接続され、全結合層の出力サイズは 12、2 番目と 3 番目の全結合層の後には加算層がある。
2 番目と 3 番目の全結合層についてのスキップ接続。加算層を使用。
応答の数と一致する出力サイズをもつ最終全結合層。

inputSize = size(XTrain,2);
outputSize = size(YTrain,2);

net = dlnetwork;

layers = [
    featureInputLayer(inputSize)
    fullyConnectedLayer(12)
    reluLayer(Name="relu1")

    fullyConnectedLayer(12)

    additionLayer(2,Name="add2")
    reluLayer(Name="relu2")

    fullyConnectedLayer(12)
    additionLayer(2,Name="add3")
    reluLayer

    fullyConnectedLayer(outputSize)];

net = addLayers(net,layers);
net = connectLayers(net,"relu1","add2/in2");
net = connectLayers(net,"relu2","add3/in2");

ニューラルネットワークアーキテクチャをプロットで可視化します。

figure
plot(net)

Figure contains an axes object. The axes object contains an object of type graphplot.

ニューラルネットワーク回帰モデルに学習させます。

Mdl = fitrnet(XTrain,YTrain,Network=net,Standardize=true)

Mdl = 
  RegressionNeuralNetwork
             ResponseName: 'Y'
    CategoricalPredictors: []
        ResponseTransform: 'none'
          NumObservations: 319
               LayerSizes: []
              Activations: ''
    OutputLayerActivation: ''
                   Solver: 'LBFGS'
          ConvergenceInfo: [1×1 struct]
          TrainingHistory: [1000×5 table]

  View network information using dlnetwork.


  Properties, Methods

検定の平均二乗誤差 (MSE) を計算して、テストセットで回帰モデルの性能を評価します。値が小さいほど、予測精度が高いことを示します。

testMSE = loss(Mdl,XTest,YTest)

testMSE = 
14.3926

検証データを使用したニューラルネットワーク学習の早期停止

学習プロセスの各反復でニューラルネットワークの検証損失を計算します。検証損失が妥当な値まで小さくなったら、その時点で学習プロセスを早期に停止します。

patients データセットを読み込みます。データセットから table を作成します。各行が 1 人の患者に対応し、各列が診断の変数に対応します。変数 Systolic を応答変数として使用し、残りの変数を予測子として使用します。

load patients
tbl = table(Age,Diastolic,Gender,Height,Smoker,Weight,Systolic);

データを学習セット tblTrain と検証セット tblValidation に分割します。観測値の約 30% が検証データ用に予約され、残りの観測値が学習データセットに使用されます。

rng("default") % For reproducibility of the partition
c = cvpartition(size(tbl,1),"Holdout",0.30);
trainingIndices = training(c);
validationIndices = test(c);
tblTrain = tbl(trainingIndices,:);
tblValidation = tbl(validationIndices,:);

学習セットを使用してニューラルネットワーク回帰モデルに学習させます。tblTrain の列 Systolic を応答変数として指定します。検証セットを使用して各反復でモデルを評価します。名前と値の引数 Verbose を使用して、各反復で学習データを表示するように指定します。既定では、検証損失が 6 回連続でそれまでに計算された検証損失の最小値以上になると、その時点で学習プロセスが早期に終了します。検証損失が最小値以上になる許容回数を変更するには、名前と値の引数 ValidationPatience を指定します。

Mdl = fitrnet(tblTrain,"Systolic", ...
    "ValidationData",tblValidation, ...
    "Verbose",1);

|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|           1|  516.021993| 3220.880047|    0.644473|    0.009854|  568.289202|           0|
|           2|  313.056754|  229.931405|    0.067026|    0.004410|  304.023695|           0|
|           3|  308.461807|  277.166516|    0.011122|    0.001426|  296.935608|           0|
|           4|  262.492770|  844.627934|    0.143022|    0.000418|  240.559640|           0|
|           5|  169.558740| 1131.714363|    0.336463|    0.000313|  152.531663|           0|
|           6|   89.134368|  362.084104|    0.382677|    0.000703|   83.147478|           0|
|           7|   83.309729|  994.830303|    0.199923|    0.000327|   76.634122|           0|
|           8|   70.731524|  327.637362|    0.041366|    0.000306|   66.421750|           0|
|           9|   66.650091|  124.369963|    0.125232|    0.000286|   65.914063|           0|
|          10|   66.404753|   36.699328|    0.016768|    0.000315|   65.357335|           0|
|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|          11|   66.357143|   46.712988|    0.009405|    0.000916|   65.306106|           0|
|          12|   66.268225|   54.079264|    0.007953|    0.000891|   65.234391|           0|
|          13|   65.788550|   99.453225|    0.030942|    0.000306|   64.869708|           0|
|          14|   64.821095|  186.344649|    0.048078|    0.000290|   64.191533|           0|
|          15|   62.353896|  319.273873|    0.107160|    0.000303|   62.618374|           0|
|          16|   57.836593|  447.826470|    0.184985|    0.000309|   60.087065|           0|
|          17|   51.188884|  524.631067|    0.253062|    0.000305|   56.646294|           0|
|          18|   41.755601|  189.072516|    0.318515|    0.000346|   49.046823|           0|
|          19|   37.539854|   78.602559|    0.382284|    0.000297|   44.633562|           0|
|          20|   36.845322|  151.837884|    0.211286|    0.000282|   47.291367|           1|
|==========================================================================================|
| Iteration  | Train Loss | Gradient   | Step       | Iteration  | Validation | Validation |
|            |            |            |            | Time (sec) | Loss       | Checks     |
|==========================================================================================|
|          21|   36.218289|   62.826818|    0.142748|    0.000316|   46.139104|           2|
|          22|   35.776921|   53.606315|    0.215188|    0.000321|   46.170460|           3|
|          23|   35.729085|   24.400342|    0.060096|    0.001018|   45.318023|           4|
|          24|   35.622031|    9.602277|    0.121153|    0.000311|   45.791861|           5|
|          25|   35.573317|   10.735070|    0.126854|    0.000397|   46.062826|           6|
|==========================================================================================|

各反復における学習平均二乗誤差 (MSE) と検証 MSE を比較するプロットを作成します。既定では、fitrnet はオブジェクト Mdl の TrainingHistory プロパティに損失の情報を格納します。この情報にドット表記を使用してアクセスできます。

iteration = Mdl.TrainingHistory.Iteration;
trainLosses = Mdl.TrainingHistory.TrainingLoss;
valLosses = Mdl.TrainingHistory.ValidationLoss;
plot(iteration,trainLosses,iteration,valLosses)
legend(["Training","Validation"])
xlabel("Iteration")
ylabel("Mean Squared Error")

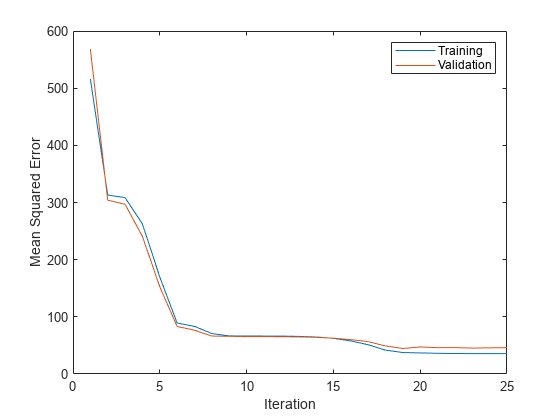
Figure contains an axes object. The axes object with xlabel Iteration, ylabel Mean Squared Error contains 2 objects of type line. These objects represent Training, Validation.

検証 MSE が最小になる対応する反復を確認します。最終的に返されるモデル Mdl は、この反復で学習させたモデルになります。

[~,minIdx] = min(valLosses);
iteration(minIdx)

ans = 
19

交差検証を使用したニューラルネットワークの適切な正則化強度の特定

ニューラルネットワークモデルの交差検証損失をさまざまな正則化強度で評価し、モデルの性能が最も高くなる対応する正則化強度を選択します。

load carbig
cars = table(Acceleration,Displacement,Horsepower, ...
    Model_Year,Origin,Weight,MPG);

cars から table に欠損値がある行を削除します。

cars = rmmissing(cars);

米国製かどうかに基づいて、自動車を分類します。

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan", ...
    "Germany","Sweden","Italy","England"],"NotUSA");

5 分割交差検証用に cvpartition オブジェクトを作成します。cvp を使用して、各分割の観測値の数がほぼ同じになるようにデータを 5 つの分割に分割します。分割の再現性を得るため、乱数シードを既定値に設定します。

rng("default")
n = size(cars,1);
cvp = cvpartition(n,"KFold",5);

さまざまな正則化強度でニューラルネットワーク回帰モデルの交差検証平均二乗誤差 (MSE) を計算します。1/n に基づく正則化強度を試します。n は観測値の数です。ニューラルネットワークモデルに学習させる前にデータを標準化するように指定します。

1/n

ans = 0.0026

lambda = (0:0.5:5)*1e-3;
cvloss = zeros(length(lambda),1);
for i = 1:length(lambda)
    cvMdl = fitrnet(cars,"MPG","Lambda",lambda(i), ...
        "CVPartition",cvp,"Standardize",true);
    cvloss(i) = kfoldLoss(cvMdl);
end

結果をプロットします。最小の交差検証 MSE に対応する正則化強度を求めます。

plot(lambda,cvloss)
xlabel("Regularization Strength")
ylabel("Cross-Validation Loss")

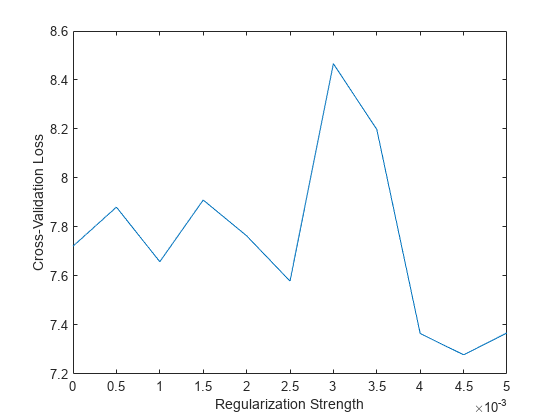
Figure contains an axes object. The axes object with xlabel Regularization Strength, ylabel Cross-Validation Loss contains an object of type line.

[~,idx] = min(cvloss);
bestLambda = lambda(idx)

bestLambda = 0.0045

正則化強度 bestLambda を使用してニューラルネットワーク回帰モデルに学習させます。

Mdl = fitrnet(cars,"MPG","Lambda",bestLambda, ...
    "Standardize",true)

Mdl = 
  RegressionNeuralNetwork
           PredictorNames: {'Acceleration'  'Displacement'  'Horsepower'  'Model_Year'  'Origin'  'Weight'}
             ResponseName: 'MPG'
    CategoricalPredictors: 5
        ResponseTransform: 'none'
          NumObservations: 392
               LayerSizes: 10
              Activations: 'relu'
    OutputLayerActivation: 'none'
                   Solver: 'LBFGS'
          ConvergenceInfo: [1×1 struct]
          TrainingHistory: [761×7 table]


  Properties, Methods

ニューラルネットワークの交差検証誤差の最小化

OptimizeHyperparameters 引数を使用して、誤差の小さいニューラルネットワークを作成します。この引数により、fitrnet はベイズ最適化を使用し、問題のある一部のハイパーパラメーターに対して交差検証損失を最小化します。

load carbig
cars = table(Acceleration,Displacement,Horsepower, ...
    Model_Year,Origin,Weight,MPG);

cars から table に欠損値がある行を削除します。

cars = rmmissing(cars);

米国製かどうかに基づいて、自動車を分類します。

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan",...
    "Germany","Sweden","Italy","England"],"NotUSA");

rng("default") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);
trainingIdx = training(c); % Training set indices
carsTrain = cars(trainingIdx,:);
testIdx = test(c); % Test set indices
carsTest = cars(testIdx,:);

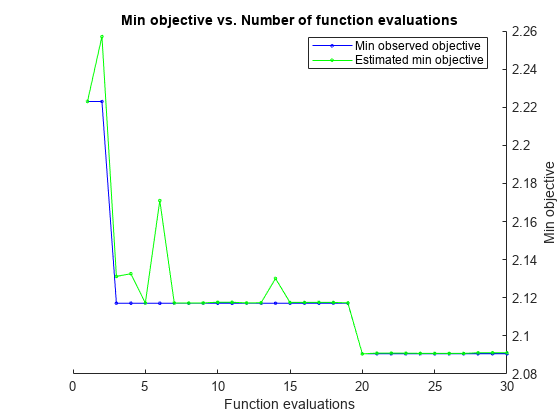
"auto" に設定された OptimizeHyperparameters 引数を使用して、回帰ニューラルネットワークに学習させます。再現性を得るために、HyperparameterOptimizationOptions 構造体の AcquisitionFunctionName を "expected-improvement-plus" に設定します。fitrnet は、既定ではベイズ最適化を実行します。グリッド探索またはランダム探索を使用するために、HyperparameterOptimizationOptions の Optimizer フィールドを設定します。

rng("default") % For reproducibility
Mdl = fitrnet(carsTrain,"MPG","OptimizeHyperparameters","auto", ...
    "HyperparameterOptimizationOptions",struct("AcquisitionFunctionName","expected-improvement-plus"))

|============================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  Activations |  Standardize |       Lambda |            LayerSizes |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |                       |
|============================================================================================================================================|
|    1 | Best   |       2.223 |       9.231 |       2.223 |       2.223 |         relu |         true |        3.841 | [101  47  15]         |
|    2 | Accept |      3.0797 |      6.4178 |       2.223 |      2.2571 |      sigmoid |        false |   7.5401e-07 | [100  17]             |
|    3 | Best   |      2.1171 |      2.4398 |      2.1171 |      2.1312 |         relu |         true |      0.01569 |  15                   |
|    4 | Accept |      2.5142 |      4.2068 |      2.1171 |      2.1326 |         none |         true |   0.00016461 | [  2 145   8]         |
|    5 | Accept |      3.0246 |     0.26994 |      2.1171 |      2.1172 |         relu |         true |   5.4264e-08 |  1                    |
|    6 | Accept |      2.9859 |     0.77249 |      2.1171 |       2.171 |         relu |         true |       0.1243 | [  5   1]             |
|    7 | Accept |        2.14 |      2.5549 |      2.1171 |      2.1173 |         relu |         true |    0.0082696 |  17                   |
|    8 | Accept |      2.7596 |     0.41156 |      2.1171 |      2.1173 |         relu |         true |       5.8567 |  72                   |
|    9 | Accept |      3.0702 |      6.3673 |      2.1171 |      2.1173 |         relu |         true |   4.4611e-07 | [ 77  24  12]         |
|   10 | Accept |      2.2126 |      1.8954 |      2.1171 |      2.1177 |         relu |         true |   4.1722e-07 |  9                    |
|   11 | Accept |      2.9998 |      16.958 |      2.1171 |      2.1177 |         relu |         true |   0.00088575 | [250  47  63]         |
|   12 | Accept |      3.3504 |      11.524 |      2.1171 |      2.1173 |         relu |         true |   1.2716e-06 | [103  55  15]         |
|   13 | Accept |       2.223 |      1.7197 |      2.1171 |      2.1174 |         relu |         true |    0.0003368 |  10                   |
|   14 | Accept |      6.4098 |     0.22799 |      2.1171 |      2.1301 |         relu |         true |       251.71 | [ 67  34 275]         |
|   15 | Accept |       6.412 |     0.12626 |      2.1171 |      2.1175 |         relu |         true |       298.04 | [ 30  23  10]         |
|   16 | Accept |      2.1882 |      1.6043 |      2.1171 |      2.1176 |         relu |         true |   5.2998e-05 |  6                    |
|   17 | Accept |      2.5141 |     0.46234 |      2.1171 |      2.1176 |         none |         true |    0.0031007 |  4                    |
|   18 | Accept |      2.5139 |      2.2299 |      2.1171 |      2.1176 |         none |         true |      0.07401 | [ 33  16  83]         |
|   19 | Accept |      2.5756 |     0.10945 |      2.1171 |      2.1173 |         none |         true |       1.6796 |  2                    |
|   20 | Best   |      2.0906 |      8.1833 |      2.0906 |      2.0906 |         relu |         true |      0.58373 | [ 13  58  65]         |
|============================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  Activations |  Standardize |       Lambda |            LayerSizes |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |                       |
|============================================================================================================================================|
|   21 | Accept |      2.4488 |      2.5839 |      2.0906 |       2.091 |         relu |         true |   3.4514e-06 |  26                   |
|   22 | Accept |      2.5142 |      3.9131 |      2.0906 |       2.091 |         none |         true |   3.9367e-06 |  255                  |
|   23 | Accept |      2.5142 |     0.21115 |      2.0906 |      2.0909 |         none |         true |   9.1909e-08 | [ 27  12  14]         |
|   24 | Accept |      6.3852 |     0.32065 |      2.0906 |      2.0908 |         none |         true |       91.409 | [ 27 193  71]         |
|   25 | Accept |      2.5312 |      15.695 |      2.0906 |      2.0908 |      sigmoid |        false |      0.00062 | [165  66]             |
|   26 | Accept |       2.588 |      4.0838 |      2.0906 |      2.0908 |      sigmoid |        false |     0.035987 |  100                  |
|   27 | Accept |      3.9253 |      6.7469 |      2.0906 |      2.0908 |      sigmoid |        false |       3.0045 | [  5 296]             |
|   28 | Accept |      2.1903 |      8.4032 |      2.0906 |      2.0911 |         relu |         true |       1.1661 | [  3 300 232]         |
|   29 | Accept |      2.5142 |      2.5771 |      2.0906 |      2.0912 |         none |         true |    1.636e-06 | [  1 294  27]         |
|   30 | Accept |      2.1336 |      6.7976 |      2.0906 |      2.0911 |         relu |         true |     0.039606 | [  4 299]             |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 138.7963 seconds
Total objective function evaluation time: 129.0442

Best observed feasible point:
    Activations    Standardize    Lambda       LayerSizes  
    ___________    ___________    _______    ______________

       relu           true        0.58373    13    58    65

Observed objective function value = 2.0906
Estimated objective function value = 2.0911
Function evaluation time = 8.1833

Best estimated feasible point (according to models):
    Activations    Standardize    Lambda       LayerSizes  
    ___________    ___________    _______    ______________

       relu           true        0.58373    13    58    65

Estimated objective function value = 2.0911
Estimated function evaluation time = 8.1846

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

Mdl = 
  RegressionNeuralNetwork
                       PredictorNames: {'Acceleration'  'Displacement'  'Horsepower'  'Model_Year'  'Origin'  'Weight'}
                         ResponseName: 'MPG'
                CategoricalPredictors: 5
                    ResponseTransform: 'none'
                      NumObservations: 314
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]
                           LayerSizes: [13 58 65]
                          Activations: 'relu'
                OutputLayerActivation: 'none'
                               Solver: 'LBFGS'
                      ConvergenceInfo: [1×1 struct]
                      TrainingHistory: [1000×7 table]


  Properties, Methods

テストデータセットで、結果のモデルの平均二乗誤差を求めます。

testMSE = loss(Mdl,carsTest,"MPG")

testMSE = 7.3273

ニューラルネットワークのカスタムハイパーパラメーターの最適化

OptimizeHyperparameters 引数を使用して、誤差の小さいニューラルネットワークを作成します。この引数により、fitrnet は交差検証誤差の小さいモデルを与えるハイパーパラメーターを検索します。関数 hyperparameters を使用して、使用する層数および層のサイズの範囲に既定より大きい値を指定します。

load carbig
cars = table(Acceleration,Displacement,Horsepower, ...
    Model_Year,Origin,Weight,MPG);

cars から table に欠損値がある行を削除します。

cars = rmmissing(cars);

米国製かどうかに基づいて、自動車を分類します。

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan",...
    "Germany","Sweden","Italy","England"],"NotUSA");

rng("default") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);
trainingIdx = training(c); % Training set indices
carsTrain = cars(trainingIdx,:);
testIdx = test(c); % Test set indices
carsTest = cars(testIdx,:);

MPG 応答を当てはめるこの問題に利用可能なハイパーパラメーターをリストします。

params = hyperparameters("fitrnet",carsTrain,"MPG");
for ii = 1:length(params)
    disp(ii);disp(params(ii))
end

     1

  optimizableVariable with properties:

         Name: 'NumLayers'
        Range: [1 3]
         Type: 'integer'
    Transform: 'none'
     Optimize: 1

     2

  optimizableVariable with properties:

         Name: 'Activations'
        Range: {'relu'  'tanh'  'sigmoid'  'none'}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 1

     3

  optimizableVariable with properties:

         Name: 'Standardize'
        Range: {'true'  'false'}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 1

     4

  optimizableVariable with properties:

         Name: 'Lambda'
        Range: [3.1847e-08 318.4713]
         Type: 'real'
    Transform: 'log'
     Optimize: 1

     5

  optimizableVariable with properties:

         Name: 'LayerWeightsInitializer'
        Range: {'glorot'  'he'}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 0

     6

  optimizableVariable with properties:

         Name: 'LayerBiasesInitializer'
        Range: {'zeros'  'ones'}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 0

     7

  optimizableVariable with properties:

         Name: 'Layer_1_Size'
        Range: [1 300]
         Type: 'integer'
    Transform: 'log'
     Optimize: 1

     8

  optimizableVariable with properties:

         Name: 'Layer_2_Size'
        Range: [1 300]
         Type: 'integer'
    Transform: 'log'
     Optimize: 1

     9

  optimizableVariable with properties:

         Name: 'Layer_3_Size'
        Range: [1 300]
         Type: 'integer'
    Transform: 'log'
     Optimize: 1

    10

  optimizableVariable with properties:

         Name: 'Layer_4_Size'
        Range: [1 300]
         Type: 'integer'
    Transform: 'log'
     Optimize: 0

    11

  optimizableVariable with properties:

         Name: 'Layer_5_Size'
        Range: [1 300]
         Type: 'integer'
    Transform: 'log'
     Optimize: 0

既定の 1 ～ 3 より多くの層を試すために、NumLayers (最適化可能な変数 1) の範囲を許容される最大サイズ [1 5] に設定します。また、Layer_4_Size および Layer_5_Size (それぞれ最適化可能な変数 10 および 11) を最適化されるように設定します。

params(1).Range = [1 5];
params(10).Optimize = true;
params(11).Optimize = true;

すべての層のサイズは、範囲 (最適化可能な変数 7 ～ 11) を既定値 [1 300] ではなく [1 400] に設定します。

for ii = 7:11
    params(ii).Range = [1 400];
end

params に設定された OptimizeHyperparameters 引数を使用して、回帰ニューラルネットワークに学習させます。再現性を得るために、HyperparameterOptimizationOptions 構造体の AcquisitionFunctionName を "expected-improvement-plus" に設定します。より適切な解を得るために、最適化のステップ数を既定値の 30 ではなく 60 に設定します。

rng("default") % For reproducibility
Mdl = fitrnet(carsTrain,"MPG","OptimizeHyperparameters",params, ...
    "HyperparameterOptimizationOptions", ...
    struct("AcquisitionFunctionName","expected-improvement-plus", ...
    "MaxObjectiveEvaluations",60))

|============================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  Activations |  Standardize |       Lambda |            LayerSizes |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |                       |
|============================================================================================================================================|
|    1 | Best   |      4.9294 |     0.35241 |      4.9294 |      4.9294 |      sigmoid |        false |       70.242 | [  3  22 223]         |
|    2 | Best   |       2.211 |       3.976 |       2.211 |      2.3191 |         relu |         true |     0.089397 | [  2  95]             |
|    3 | Accept |      2.7225 |      23.043 |       2.211 |      2.2929 |      sigmoid |        false |   2.5899e-07 | [303  60  59]         |
|    4 | Accept |      3.5246 |      4.4994 |       2.211 |      2.2883 |         relu |        false |   5.1748e-05 | [102   5  15   1]     |
|    5 | Accept |      2.2357 |      3.2875 |       2.211 |      2.2164 |         relu |         true |     0.095678 | [  2  68]             |
|    6 | Accept |      3.0174 |      1.3174 |       2.211 |      2.2144 |         relu |         true |    0.0031767 | [  2   1]             |
|    7 | Accept |      2.3385 |     0.64635 |       2.211 |      2.2199 |         relu |         true |     0.043248 |  2                    |
|    8 | Accept |      4.8512 |     0.52613 |       2.211 |      2.2199 |         relu |         true |        3.387 | [  2  23   5   1]     |
|    9 | Accept |      2.4583 |     0.16388 |       2.211 |      2.2236 |         relu |         true |       1.0849 | [  1  10]             |
|   10 | Accept |      3.1863 |      3.8647 |       2.211 |      2.2237 |         relu |         true |     0.061861 | [ 63   1   1 112]     |
|   11 | Accept |      3.8592 |      3.3615 |       2.211 |      2.2235 |         relu |         true |      0.20233 | [  2  45   1   4  59] |
|   12 | Accept |      3.3752 |      3.4719 |       2.211 |      2.2111 |         relu |         true |    1.556e-05 | [  4  18   1 104]     |
|   13 | Accept |      6.4116 |     0.15784 |       2.211 |      2.2198 |         relu |         true |       287.34 | [ 34 196]             |
|   14 | Accept |      2.3537 |     0.21589 |       2.211 |      2.2104 |         relu |         true |       5.3986 | [  2  12]             |
|   15 | Accept |      3.1122 |    0.077105 |       2.211 |      2.2109 |         relu |         true |       7.2543 |  1                    |
|   16 | Accept |      6.4092 |     0.11676 |       2.211 |      2.2142 |         relu |         true |       241.19 | [  1 389]             |
|   17 | Best   |      2.1517 |     0.69926 |      2.1517 |      2.1523 |         relu |         true |      0.24096 |  4                    |
|   18 | Best   |      2.1273 |     0.87139 |      2.1273 |      2.1274 |         relu |         true |      0.11077 |  5                    |
|   19 | Accept |      4.1318 |     0.14418 |      2.1273 |      2.1274 |      sigmoid |        false |   4.8026e-06 | [ 12 106  59]         |
|   20 | Accept |      2.2859 |     0.61843 |      2.1273 |      2.1269 |         relu |         true |       8.3707 | [  2   9   1   5   9] |
|============================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  Activations |  Standardize |       Lambda |            LayerSizes |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |                       |
|============================================================================================================================================|
|   21 | Accept |      2.1981 |      11.621 |      2.1273 |      2.1265 |         relu |         true |       4.0719 | [203 124   1  62]     |
|   22 | Accept |      4.1318 |       0.117 |      2.1273 |      2.1269 |      sigmoid |        false |   5.7744e-08 | [317   4  60   1]     |
|   23 | Accept |      2.9406 |      2.6457 |      2.1273 |      2.1268 |         relu |         true |       7.2868 | [ 23   7   1 373]     |
|   24 | Accept |      5.4267 |     0.15109 |      2.1273 |      2.1276 |         relu |         true |       3.4444 | [  1 253   1]         |
|   25 | Accept |      3.5359 |      1.7515 |      2.1273 |      2.1276 |         relu |         true |       36.471 | [ 51   3 204  71]     |
|   26 | Accept |      4.1542 |      1.3619 |      2.1273 |      2.1276 |         relu |         true |       1.2334 | [  5   4   1  95]     |
|   27 | Accept |      2.3033 |      15.761 |      2.1273 |      2.1276 |         relu |         true |     0.028889 | [ 42 348]             |
|   28 | Accept |      4.1318 |    0.093199 |      2.1273 |      2.1276 |      sigmoid |        false |   5.9314e-08 | [109   9]             |
|   29 | Accept |      3.0644 |       18.95 |      2.1273 |      2.1276 |      sigmoid |        false |   3.2982e-08 | [388   3 331]         |
|   30 | Accept |      2.8076 |      4.1115 |      2.1273 |      2.1277 |         relu |         true |   0.00077627 |  183                  |
|   31 | Accept |      3.3041 |      3.4421 |      2.1273 |      2.1277 |         relu |         true |   2.1595e-05 |  116                  |
|   32 | Accept |      3.1379 |      11.325 |      2.1273 |      2.1276 |         relu |         true |   2.2732e-05 | [187  41]             |
|   33 | Accept |      3.3071 |      6.2584 |      2.1273 |      2.1277 |         relu |         true |   2.7221e-07 | [120  23]             |
|   34 | Accept |      2.2511 |      4.5188 |      2.1273 |      2.1277 |         relu |         true |       2.6888 | [  2 104 142  60]     |
|   35 | Accept |      2.3491 |      7.7419 |      2.1273 |      2.1277 |         relu |         true |       4.3755 | [  1 322 277  53]     |
|   36 | Accept |      6.3658 |      0.2106 |      2.1273 |       2.129 |         relu |         true |       60.596 | [  4  17  12  47]     |
|   37 | Accept |      2.1727 |      4.9758 |      2.1273 |      2.1291 |         relu |         true |    0.0059602 | [  2 110]             |
|   38 | Accept |      2.5005 |      28.335 |      2.1273 |      2.1288 |         relu |         true |     0.052893 | [252  99 208  55]     |
|   39 | Accept |      2.2474 |       31.45 |      2.1273 |      2.1301 |         relu |         true |        6.086 | [356 136 307  70]     |
|   40 | Best   |      2.0745 |      37.552 |      2.0745 |      2.0746 |         relu |         true |      0.55888 | [288 115 213 120]     |
|============================================================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |  Activations |  Standardize |       Lambda |            LayerSizes |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |              |                       |
|============================================================================================================================================|
|   41 | Accept |      2.0896 |      26.315 |      2.0745 |      2.0747 |         relu |         true |      0.98992 | [270  74 258  28]     |
|   42 | Accept |      4.1421 |     0.53203 |      2.0745 |      2.0746 |         relu |         true |       13.353 | [  4 376   1 149]     |
|   43 | Accept |      2.6447 |      5.5647 |      2.0745 |      2.0746 |         relu |         true |     0.026383 | [ 18 118   1  23]     |
|   44 | Accept |      2.4817 |      27.009 |      2.0745 |      2.0747 |         relu |         true |     0.013213 | [389 175]             |
|   45 | Accept |      2.3857 |      6.6975 |      2.0745 |      2.0746 |         relu |         true |    0.0012278 | [  4 386]             |
|   46 | Accept |      2.0888 |      6.0115 |      2.0745 |      2.0746 |         relu |         true |      0.12715 |  354                  |
|   47 | Accept |      4.0279 |       1.866 |      2.0745 |      2.0747 |         relu |         true |       3.1997 | [  8  46   1   7]     |
|   48 | Accept |      2.1107 |      3.9274 |      2.0745 |      2.0747 |         relu |         true |      0.87573 | [ 75   3]             |
|   49 | Accept |      2.8679 |      17.581 |      2.0745 |      2.0747 |         relu |         true |     0.014349 | [382  19   2 217]     |
|   50 | Accept |        2.12 |      31.823 |      2.0745 |      2.0748 |         relu |         true |       1.4981 | [  9 250 205 316]     |
|   51 | Accept |      2.0956 |      9.3003 |      2.0745 |      2.0749 |         relu |         true |      0.50519 | [ 13  25 234]         |
|   52 | Accept |      2.0788 |      20.963 |      2.0745 |      2.0748 |         relu |         true |      0.20245 | [ 30 340  72]         |
|   53 | Accept |      2.0793 |      15.073 |      2.0745 |      2.0749 |         relu |         true |      0.30508 | [230  27 157]         |
|   54 | Best   |      2.0571 |      14.353 |      2.0571 |      2.0572 |         relu |         true |      0.40191 | [ 58  58  83   4]     |
|   55 | Accept |      2.2477 |      5.5372 |      2.0571 |      2.0572 |         relu |         true |     0.056099 | [  8   2 166]         |
|   56 | Accept |      2.2329 |      9.6228 |      2.0571 |      2.0571 |         relu |         true |      0.15146 | [  1  46 169   9]     |
|   57 | Accept |      2.2506 |      11.931 |      2.0571 |      2.0571 |         relu |         true |    0.0068432 | [  2 263  19]         |
|   58 | Accept |      2.2439 |      6.1584 |      2.0571 |      2.0572 |         relu |         true |    0.0037586 | [  2 191   2]         |
|   59 | Accept |      6.3612 |     0.15672 |      2.0571 |      2.0572 |         relu |         true |       56.064 | [ 19   2   2   1   9] |
|   60 | Accept |      2.7839 |      5.6539 |      2.0571 |      2.0573 |         relu |         true |     0.011315 | [ 18  33  49]         |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 60 reached.
Total function evaluations: 60
Total elapsed time: 494.8036 seconds
Total objective function evaluation time: 469.8626

Best observed feasible point:
    Activations    Standardize    Lambda          LayerSizes     
    ___________    ___________    _______    ____________________

       relu           true        0.40191    58    58    83     4

Observed objective function value = 2.0571
Estimated objective function value = 2.0573
Function evaluation time = 14.3527

Best estimated feasible point (according to models):
    Activations    Standardize    Lambda          LayerSizes     
    ___________    ___________    _______    ____________________

       relu           true        0.40191    58    58    83     4

Estimated objective function value = 2.0573
Estimated function evaluation time = 14.3565

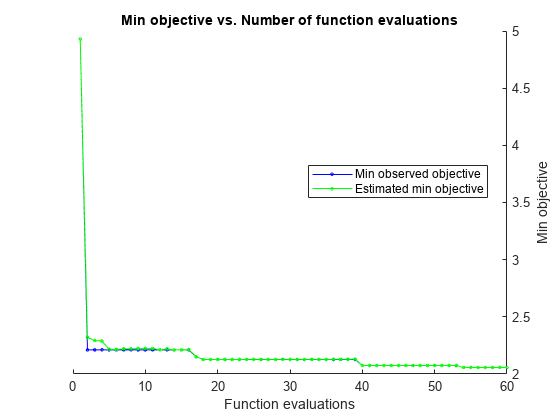
Mdl = 
  RegressionNeuralNetwork
                       PredictorNames: {'Acceleration'  'Displacement'  'Horsepower'  'Model_Year'  'Origin'  'Weight'}
                         ResponseName: 'MPG'
                CategoricalPredictors: 5
                    ResponseTransform: 'none'
                      NumObservations: 314
    HyperparameterOptimizationResults: [1×1 BayesianOptimization]
                           LayerSizes: [58 58 83 4]
                          Activations: 'relu'
                OutputLayerActivation: 'none'
                               Solver: 'LBFGS'
                      ConvergenceInfo: [1×1 struct]
                      TrainingHistory: [1000×7 table]


  Properties, Methods

テストデータセットで、結果のモデルの平均二乗誤差を求めます。

testMSE = loss(Mdl,carsTest,"MPG")

testMSE = 7.1939

ニューラルネットワークでの複数の応答変数の指定

R2024b 以降

複数の応答変数をもつ回帰ニューラルネットワークを作成します。

carbig データセットを読み込みます。このデータセットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。Displacement や Horsepower などの予測子変数と応答変数の Acceleration および MPG が格納された table を作成します。table の最初の 8 行を表示します。

load carbig
cars = table(Displacement,Horsepower,Model_Year, ...
    Origin,Weight,Acceleration,MPG);
head(cars)

    Displacement    Horsepower    Model_Year    Origin     Weight    Acceleration    MPG
    ____________    __________    __________    _______    ______    ____________    ___

        307            130            70        USA         3504           12        18 
        350            165            70        USA         3693         11.5        15 
        318            150            70        USA         3436           11        18 
        304            150            70        USA         3433           12        16 
        302            140            70        USA         3449         10.5        17 
        429            198            70        USA         4341           10        15 
        454            220            70        USA         4354            9        14 
        440            215            70        USA         4312          8.5        14

cars から table に欠損値がある行を削除します。

cars = rmmissing(cars);

米国製かどうかに基づいて、自動車を分類します。

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan",...
    "Germany","Sweden","Italy","England"],"NotUSA");

データを学習セットとテストセットに分割します。観測値の約 85% をニューラルネットワークモデルの学習に使用し、観測値の約 15% を学習済みモデルの新しいデータでの性能のテストに使用します。cvpartition を使用してデータを分割します。

rng("default") % For reproducibility
c = cvpartition(height(cars),"Holdout",0.15);
carsTrain = cars(training(c),:);
carsTest = cars(test(c),:);

学習データ carsTrain を fitrnet 関数に渡して、多重応答ニューラルネットワーク回帰モデルに学習させます。より良い結果を得るために、予測子データを標準化するように指定します。

Mdl = fitrnet(carsTrain,["Acceleration","MPG"], ...
    Standardize=true)

Mdl = 
  RegressionNeuralNetwork
           PredictorNames: {'Displacement'  'Horsepower'  'Model_Year'  'Origin'  'Weight'}
             ResponseName: {'Acceleration'  'MPG'}
    CategoricalPredictors: 4
        ResponseTransform: 'none'
          NumObservations: 334
               LayerSizes: 10
              Activations: 'relu'
    OutputLayerActivation: 'none'
                   Solver: 'LBFGS'
          ConvergenceInfo: [1×1 struct]
          TrainingHistory: [1000×7 table]


  Properties, Methods

Mdl は学習させた RegressionNeuralNetwork モデルです。ドット表記を使用して Mdl のプロパティにアクセスできます。たとえば、Mdl.ConvergenceInfo と指定すると、モデルの収束についての詳細情報を取得できます。

検定の平均二乗誤差 (MSE) を計算して、テストセットで回帰モデルの性能を評価します。MSE の値が小さいほど、パフォーマンスが優れていることを示します。名前と値の引数 OutputType を "per-response" に設定して、各応答変数の損失を個別に返します。

testMSE = loss(Mdl,carsTest,["Acceleration","MPG"], ...
    OutputType="per-response")

testMSE = 1×2

    1.5341    4.8245

テストセット内の観測値に対する応答値を予測します。予測された応答値を table として返します。

predictedY = predict(Mdl,carsTest,OutputType="table")

predictedY=58×2 table
    Acceleration     MPG  
    ____________    ______

       9.3612       13.567
       15.655       21.406
       17.921       17.851
       11.139       13.433
       12.696        10.32
       16.498       17.977
       16.227       22.016
       12.165       12.926
       12.691       12.072
       12.424       14.481
       16.974       22.152
       15.504       24.955
       11.068       13.874
       11.978       12.664
       14.926       10.134
       15.638       24.839
      ⋮

入力引数

`Tbl` — 標本データ
table

モデルを学習させるために使用する標本データ。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

必要に応じて、Tbl に応答変数用の列と観測値の重み用の列を含めることができます。それぞれの応答変数と重みの値は数値ベクトルでなければなりません。
Tbl 内の応答変数は ResponseVarName または formula を使用して指定し、Tbl 内の観測値の重みは Weights を使用して指定しなければなりません。
- ResponseVarName を使用して応答変数を指定すると、fitrnet は残りの変数を予測子として使用します。Tbl 内の残りの変数のサブセットを予測子として使用するには、PredictorNames を使用して予測子変数を指定します。
- formula を使用してモデル仕様を定義すると、fitrnet は formula の指定に従って Tbl 内の変数のサブセットを予測子変数および応答変数として使用します。
Tbl に応答変数が含まれていない場合は、Y を使用して指定します。Y がベクトルの場合、応答変数の長さと Tbl の行数が等しくなければなりません。Y が行列の場合、Y と Tbl の行数が同じでなければなりません。Tbl 内の変数のサブセットを予測子として使用するには、PredictorNames を使用して予測子変数を指定します。

データ型: table

`ResponseVarName` — 応答変数の名前
`Tbl` 内の変数の名前

応答変数の名前。Tbl 内の変数の名前として指定します。各応答変数は数値ベクトルでなければなりません。

ResponseVarName は、文字ベクトル、string 配列、または文字ベクトルの cell 配列として指定しなければなりません。たとえば、応答変数 Y が Tbl に Tbl.Y として格納されている場合、"Y" を指定します。それ以外の場合、Tbl の Y の列は、モデルに学習させるときに予測子として扱われます。

データ型: char | string | cell

`formula` — 応答変数および予測子変数サブセットの説明モデル
文字ベクトル | string スカラー

応答変数および予測子変数サブセットの説明モデル。"Y1,Y2~x1+x2+x3" という形式の文字ベクトルまたは string スカラーとして指定します。この形式で、Y1 と Y2 は応答変数を表し、x1、x2 および x3 は予測子変数を表します。

モデルに学習をさせるための予測子として Tbl 内の変数のサブセットを指定するには、式を使用します。式を指定する場合、観測値の重み (指定されている場合) を除き、formula に現れない Tbl 内の変数はいずれも使用されません。

式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB^® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。

データ型: char | string

`Y` — 応答データ
数値ベクトル | 数値行列 | 数値 table

応答データ。数値のベクトル、行列、または table として指定します。

応答変数を 1 つ使用するには、Y をベクトルとして指定します。Y の長さは X または Tbl の観測値の数と等しくなければなりません。
応答変数を複数使用するには、Y を各列が応答変数に対応する行列または table として指定します。Y と予測子データ (X または Tbl) の行数は同じでなければなりません。

データ型: single | double | table

`X` — 予測子データ
数値行列

モデルの学習に使用する予測子データ。数値行列として指定します。

既定では、X の各行が 1 つの観測値として扱われ、各列が 1 つの予測子として扱われます。

X と Y の観測値の数は同じでなければなりません。

予測子の名前を X に表示される順序で指定するには、名前と値の引数 PredictorNames を使用します。

メモ

観測値が列に対応するように予測子行列を配置して ObservationsIn="columns" を指定すると、計算時間が大幅に短縮される可能性があります。

データ型: single | double

メモ

1 つの応答変数をもつモデルに学習させる場合、NaN、空の文字ベクトル ('')、空の string ("")、<missing>、および <undefined> の要素は欠損値として扱われ、以下のいずれかの特性をもつ観測値は削除されます。

応答の欠損値 (たとえば、Y または ValidationData{2})
予測子の観測値 (たとえば、X または ValidationData{1} の行) 内の少なくとも 1 つの欠損値
NaN 値または重み 0 (たとえば、Weights または ValidationData{3} 内の値)

複数の応答変数をもつモデルに学習させる場合は、データ引数の欠損値を削除してから fitrnet に渡します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: fitrnet(X,Y,LayerSizes=[10 10],Activations=["relu","tanh"]) は、2 つの全結合層をもつニューラルネットワークを作成するように指定します。出力はそれぞれ 10 個です。最初の層では正規化線形ユニット (ReLU) 活性化関数を使用し、2 番目の層では双曲線正接活性化関数を使用します。

ニューラルネットワークのオプション

`LayerSizes` — 全結合層のサイズ
正の整数ベクトル | `[]`

ニューラルネットワークモデルの全結合層のサイズ。次の値のいずれかとして指定します。

正の整数のベクトル — LayerSizes の i 番目の要素は、ニューラルネットワークモデルの i 番目の全結合層の出力数です。LayerSizes には最終全結合層のサイズは含まれません。詳細については、ニューラルネットワークの構造を参照してください。
[] (R2025a 以降) — Network 引数で指定されたニューラルネットワークアーキテクチャを使用します。

Network が [] の場合、既定値は 10 です。そうでない場合、既定値は [] となります。Network 引数を使用してニューラルネットワークアーキテクチャを指定した場合、LayerSizes 引数の値を変更してはなりません。

例: LayerSizes=[100 25 10]

`Activations` — 全結合層の活性化関数
string 配列 | 文字ベクトルの cell 配列

ニューラルネットワークモデルの全結合層の活性化関数。次の値のいずれかとして指定します。

string スカラーまたは文字ベクトル — モデルのそれぞれの全結合層に、指定した活性化関数を使用します。
string 配列または文字ベクトルの cell 配列 — モデルの i 番目の全結合層に Activations の i 番目の要素を使用します。
"" (R2025a 以降) — Network 引数で指定されたニューラルネットワークアーキテクチャを使用します。

次の値を 1 つ以上使用して活性化関数を指定します。

値	説明
`"relu"`	正規化線形ユニット (ReLU) 関数 — 各入力要素に対して、0 より小さい値については 0 に設定するという次のしきい値演算を実行します。 $f (x) = {\begin{matrix} x, & x \geq 0 \\ 0, & x < 0 \end{matrix}$
`"tanh"`	双曲線正接 (tanh) 関数 — 各入力要素に関数 `tanh` を適用します。
`"sigmoid"`	シグモイド関数 — 各入力要素に対して次の演算を実行します。 $f (x) = \frac{1}{1 + e^{- x}}$
`"none"`	恒等関数 — 変換を実行せずに、各入力要素を次のようにそのまま返します。f(x) = x

Network が [] の場合、既定値は "relu" です。そうでない場合、既定値は [] となります。Network 引数を使用してニューラルネットワークアーキテクチャを指定した場合、Activations 引数の値を変更してはなりません。

例: Activations="sigmoid"

例: Activations=["relu","tanh"]

`LayerWeightsInitializer` — 全結合層の重みを初期化する関数
`"glorot"` | `"he"` | `""`

全結合層の重みを初期化する関数。次の値のいずれかとして指定します。

"glorot" — Glorot 初期化子[1] (Xavier 初期化子とも呼ばれる) を使用して重みを初期化します。Glorot 初期化子では、それぞれの層について、ゼロ平均で分散が 2/(I+O) の一様分布から個別に標本を抽出します。I は層の入力サイズ、O は出力サイズです。
"he" — He 初期化子[2]を使用して重みを初期化します。He 初期化子では、それぞれの層について、ゼロ平均で分散が 2/I の正規分布から標本を抽出します。I は層の入力サイズです。
"" (R2025a 以降) — Network 引数の層で指定されている初期化子を使用して重みを初期化します。

Network が [] の場合、既定値は "glorot" です。それ以外の場合、既定値は "" です。Network 引数を使用してニューラルネットワークアーキテクチャを指定した場合、LayerWeightsInitializer 引数の値を変更してはなりません。

例: LayerWeightsInitializer="he"

データ型: char | string

`LayerBiasesInitializer` — 全結合層の初期バイアスのタイプ
`"zeros"` | `"ones"` | `""`

全結合層の初期バイアスのタイプ。次の値のいずれかとして指定します。

"zeros" — 0 のベクトルでバイアスを初期化します。
"ones" — 1 のベクトルでバイアスを初期化します。
"" (R2025a 以降) — Network 引数の層で指定されている初期化子を使用してバイアスを初期化します。

Network が [] の場合、既定値は "zeros" です。それ以外の場合、既定値は "" です。Network 引数を使用してニューラルネットワークアーキテクチャを指定した場合、LayerBiasesInitializer 引数の値を変更してはなりません。

例: LayerBiasesInitializer="ones"

データ型: char | string

`Network` — カスタムのニューラルネットワークアーキテクチャ
`[]` (既定値) | 層配列 | `dlnetwork` オブジェクト

R2025a 以降

カスタムのニューラルネットワークアーキテクチャ。次の値のいずれかとして指定します。

[] — ニューラルネットワークアーキテクチャと LayerSizes、Activations、LayerWeightsInitializer、および LayerBiasesInitializer の引数で定義される層の構成を使用します。
層配列 (Deep Learning Toolbox™ が必要) — 層配列で指定されたニューラルネットワークアーキテクチャを使用します。利用可能な層の一覧については、深層学習層の一覧 (Deep Learning Toolbox)を参照してください。
dlnetwork オブジェクト (Deep Learning Toolbox が必要) — dlnetwork (Deep Learning Toolbox) オブジェクトで指定されたニューラルネットワークアーキテクチャを使用します。

層配列と dlnetwork の入力の場合、ネットワークの入力として、入力データの予測子の数と一致する入力サイズをもつ単一の特徴入力層が必要です。ネットワークの出力サイズは応答の数と一致しなければなりません。LayerSizes、Activations、LayerWeightsInitializer、および LayerBiasesInitializer の各引数は変更しないでください。

この引数はカテゴリカル予測子をもつ入力データをサポートしていません。

`ObservationsIn` — 予測子データにおける観測値の次元
`"rows"` (既定値) | `"columns"`

予測子データにおける観測値の次元。"rows" または "columns" として指定します。

メモ

観測値が列に対応するように予測子行列を配置して ObservationsIn="columns" を指定すると、計算時間が大幅に短縮される可能性があります。table の予測子データや多重応答回帰に対して ObservationsIn="columns" を指定することはできません。

例: ObservationsIn="columns"

データ型: char | string

`Lambda` — 正則化項の強度
`0` (既定値) | 非負のスカラー

正則化項の強度。非負のスカラーを指定します。最小化のための目的関数は、平均二乗誤差 (MSE) 損失関数とリッジ (L2) ペナルティ項から作成されます。

例: Lambda=1e-4

データ型: single | double

`Standardize` — 予測子データを標準化するためのフラグ
`false` または `0` (既定値) | `true` または `1`

予測子データを標準化するためのフラグ。数値または logical の 0 (false) または 1 (true) として指定します。Standardize を true に設定すると、各数値予測子変数が対応する列の平均値と標準偏差によってセンタリングおよびスケーリングされます。カテゴリカル予測子は標準化されません。

Network 引数を使用してニューラルネットワークアーキテクチャを指定する場合、Standardize 引数を使用して予測子を標準化するには、ネットワークの入力層で正規化を実行してはなりません。

例: Standardize=true

データ型: single | double | logical

`StandardizeResponses` — 応答データを標準化するためのフラグ
`false` または `0` (既定値) | `true` または `1`

R2024b 以降

モデルを当てはめる前に応答データを標準化するためのフラグ。数値または logical の 0 (false) または 1 (true) として指定します。StandardizeResponses を true に設定すると、各応答変数が対応する列の平均値と標準偏差によってセンタリングおよびスケーリングされます。

例: StandardizeResponses=true

データ型: single | double | logical

収束制御オプション

`Verbose` — 詳細レベル
`0` (既定値) | `1`

詳細レベル。0 または 1 として指定します。名前と値の引数 Verbose は、fitrnet がコマンドラインに表示する診断情報の量を制御します。

値	説明
`0`	`fitrnet` は診断情報を表示しません。
`1`	`fitrnet` は診断情報を定期的に表示します。

既定では、StoreHistory が true に設定され、診断情報が fitrnet で Mdl 内に格納されます。診断情報にアクセスするには Mdl.TrainingHistory を使用します。

例: Verbose=1

データ型: single | double

`VerboseFrequency` — 詳細出力の頻度
`1` (既定値) | 正の整数スカラー

詳細出力の頻度 (診断情報をコマンドラインに出力するまでの反復回数)。正の整数スカラーとして指定します。値 1 は、1 回の反復ごとに診断情報を出力することを示します。

メモ

この名前と値の引数を使用するには、Verbose を 1 に設定しなければなりません。

例: VerboseFrequency=5

データ型: single | double

`StoreHistory` — 学習履歴を格納するためのフラグ
`true` または `1` (既定値) | `false` または `0`

学習履歴を格納するためのフラグ。数値または logical の 0 (false) または 1 (true) として指定します。StoreHistory を true に設定すると、診断情報が Mdl 内に格納され、Mdl.TrainingHistory を使用してアクセスできます。

例: StoreHistory=false

データ型: single | double | logical

`InitialStepSize` — 初期ステップサイズ
`[]` (既定値) | 正のスカラー | `"auto"`

初期ステップサイズ。正のスカラーまたは "auto" として指定します。既定では、fitrnet は、モデルの学習に使用されるヘッシアンの初期近似の決定に初期ステップサイズを使用しません (学習ソルバーを参照)。ただし、初期ステップサイズ ${‖ s_{0} ‖}_{\infty}$ を指定すると、逆ヘッシアンの初期近似は $\frac{{‖ s_{0} ‖}_{\infty}}{{‖ \nabla ℒ_{0} ‖}_{\infty}} I$ になります。 $\nabla ℒ_{0}$ は初期勾配ベクトル、 $I$ は単位行列です。

fitrnet で自動的に初期ステップサイズを決定するには、値を "auto" として指定します。この場合、関数で ${‖ s_{0} ‖}_{\infty} = 0.5 {‖ η_{0} ‖}_{\infty} + 0.1$ を使用して初期ステップサイズが自動的に決定されます。 $s_{0}$ は初期ステップベクトル、 $η_{0}$ は制約がない初期の重みとバイアスのベクトルです。

例: InitialStepSize="auto"

データ型: single | double | char | string

`IterationLimit` — 学習の最大反復回数
`1e3` (既定値) | 正の整数スカラー

学習の最大反復回数。正の整数スカラーとして指定します。

学習ルーチンが正常に収束したかどうかに関係なく、学習済みのモデルが返されます。Mdl.ConvergenceInfo に収束情報が格納されます。

例: IterationLimit=1e8

データ型: single | double

`GradientTolerance` — 勾配の絶対許容誤差
`1e-6` (既定値) | 非負のスカラー

勾配の絶対許容誤差。非負のスカラーとして指定します。

学習の反復 t における損失関数を $ℒ_{t}$ 、反復 t における重みとバイアスに関する損失関数の勾配を $\nabla ℒ_{t}$ 、初期点における損失関数の勾配を $\nabla ℒ_{0}$ とします。 $\max | \nabla ℒ_{t} | \leq a \cdot GradientTolerance$ ( $a = \max (1, \min | ℒ_{t} |, \max | \nabla ℒ_{0} |)$ ) になると、学習プロセスが終了します。

例: GradientTolerance=1e-5

データ型: single | double

`LossTolerance` — 損失の許容誤差
`1e-6` (既定値) | 非負のスカラー

損失の許容誤差。非負のスカラーとして指定します。

いずれかの反復において損失が LossTolerance より小さくなると、学習プロセスが終了します。

例: LossTolerance=1e-8

データ型: single | double

`StepTolerance` — ステップサイズの許容誤差
`1e-6` (既定値) | 非負のスカラー

ステップサイズの許容誤差。非負のスカラーとして指定します。

いずれかの反復においてステップサイズが StepTolerance より小さくなると、学習プロセスが終了します。

例: StepTolerance=1e-4

データ型: single | double

`ValidationData` — 学習の収束を検出するための検証データ
cell 配列 | table

学習の収束を検出するための検証データ。cell 配列または table として指定します。

学習プロセスにおいて、ValidationData を使用して検証損失が定期的に推定されます。検証損失が連続して増加した回数が ValidationPatience の回数を超えると、その時点で学習が終了します。

応答変数を含む予測子データの table Tbl を使用する場合、ValidationData を table として指定できます。この場合、ValidationData は、Tbl 内に含まれるものと同じ予測子および応答を格納していなければなりません。ソフトウェアは、Tbl が重さのベクトルを含む場合であっても、観測値に重みを適用することはありません。重みを指定するには、ValidationData を cell 配列として指定しなければなりません。

ValidationData を cell 配列として指定する場合、次の形式でなければなりません。

ValidationData{1} は、予測子データと同じデータ型および方向でなければなりません。つまり、予測子行列 X を使用する場合、ValidationData{1} は、予測子データが X と同じ方向で格納されている m 行 p 列または p 行 m 列の行列でなければなりません。学習データ X の予測子変数と ValidationData{1} の予測子変数は対応していなければなりません。同様に、予測子データの予測子 table Tbl を使用する場合、ValidationData{1} は、Tbl に含まれるものと同じ予測子変数を格納していなければなりません。ValidationData{1} と予測子データの観測値の数が同じである必要はありません。
ValidationData{2} は応答変数 (Y または ResponseVarName) のデータ型および形式と一致しなければなりません。ValidationData{2} が応答の配列である場合、その要素数は ValidationData{1} にある観測値の数と同じでなければなりません。ValidationData{1} が table である場合、ValidationData{2} はその table 内の応答変数の名前とすることができます。同じ ResponseVarName または formula を使用する場合、ValidationData{2} を [] として指定できます。
必要に応じて、ValidationData{3} を観測値の重みについての m 次元の数値ベクトル、または観測値の重みを含む table ValidationData{1} 内の変数名として指定できます。検証データに関する重みは、合計が 1 になるように正規化されます。

Network 引数を使用してニューラルネットワークアーキテクチャを指定する場合、ValidationData に観測値の重みが含まれていてはなりません。

ValidationData を指定し、コマンドラインで検証損失を表示するには、Verbose を 1 に設定します。

データ型: table | cell

`ValidationFrequency` — 検証の評価の間隔 (反復回数)
`1` (既定値) | 正の整数スカラー

検証の評価の間隔 (反復回数)。正の整数スカラーとして指定します。値 1 は、1 回の反復ごとに検証メトリクスを評価することを示します。

メモ

この名前と値の引数を使用するには、ValidationData を指定しなければなりません。

例: ValidationFrequency=5

データ型: single | double

`ValidationPatience` — 検証の評価の停止条件
`6` (既定値) | 非負の整数スカラー

検証の評価の停止条件。非負の整数スカラーとして指定します。検証損失が ValidationPatience 回連続でそれまでに計算された検証損失の最小値以上になると、その時点で学習が停止します。Mdl.TrainingHistory をチェックすると、検証損失が連続で最小値以上になっている現在までの回数 (Validation Checks) を確認できます。

例: ValidationPatience=10

データ型: single | double

メモ

検証データのオプション (ValidationData、ValidationFrequency、および ValidationPatience) は、多重応答回帰ではサポートされません。

他の回帰のオプション

`CategoricalPredictors` — カテゴリカル予測子のリスト
正の整数のベクトル | logical ベクトル | 文字行列 | string 配列 | 文字ベクトルの cell 配列 | `"all"`

カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。説明は、予測子データの行に観測値、列に予測子があると仮定しています。

値	説明
正の整数のベクトル	ベクトルの各エントリは、対応する予測子がカテゴリカルであることを示すインデックス値です。インデックス値の範囲は 1 ～ `p` です。`p` はモデルの学習に使用した予測子の数です。 `fitrnet` が入力変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。応答変数、観測値の重みの変数、または関数で使用されないその他の変数は、いずれも `CategoricalPredictors` 値でカウントされません。
logical ベクトル	`true` というエントリは、対応する予測子がカテゴリカルであることを意味します。ベクトルの長さは `p` です。
文字行列	行列の各行は予測子変数の名前です。名前は `PredictorNames` のエントリに一致しなくてはなりません。文字行列の各行が同じ長さになるように、名前を余分な空白で埋めてください。
文字ベクトルの cell 配列または string 配列	配列の各要素は予測子変数の名前です。名前は `PredictorNames` のエントリに一致しなくてはなりません。
`"all"`	すべての予測子がカテゴリカルです。

既定では、予測子データが table (Tbl) 内にある場合、fitrnet は、その変数が logical ベクトル、categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。予測子データが行列 (X) である場合、fitrnet はすべての予測子が連続的であると見なします。他の予測子をカテゴリカル予測子として指定するには、名前と値の引数 CategoricalPredictors を使用してそれらを指定します。

特定されたカテゴリカル予測子に対して、fitrnet はカテゴリカル変数に順序が設定されていないか順序が設定されているかに応じて、2 つの異なる方式を使用してダミー変数を作成します。順序付けのないカテゴリカル変数の場合、fitrnet は、そのカテゴリカル変数の各レベルについて 1 つずつダミー変数を作成します。順序付けされたカテゴリカル変数の場合、fitrnet は、カテゴリの数よりも 1 つ少ないダミー変数を作成します。詳細については、ダミー変数の自動作成を参照してください。

例: CategoricalPredictors="all"

`PredictorNames` — 予測子変数名
一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

予測子変数名。一意な名前の string 配列または一意な文字ベクトルの cell 配列として指定します。PredictorNames の機能は、学習データの提供方法によって決まります。

X と Y を指定した場合、PredictorNames を使用して X 内の予測子変数に名前を割り当てることができます。
- PredictorNames 内の名前の順序は、X の予測子の順序に一致しなければなりません。X が既定の方向 (行に観測値、列に予測子) をもつと仮定すると、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前 (以下同様) になります。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。
- 既定では PredictorNames は {'x1','x2',...} です。
Tbl を指定する場合、PredictorNames を使用して学習に使用する予測子変数を選択できます。つまり、fitrnet は、学習時に PredictorNames の変数のみを予測子として使用します。
- PredictorNames は Tbl.Properties.VariableNames のサブセットでなければならず、いずれの応答変数の名前も含めることはできません。
- 既定では、すべての予測子変数の名前が PredictorNames に格納されます。
- PredictorNames と formula の両方ではなく、いずれか一方を使用して学習用の予測子を指定することをお勧めします。

例: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]

データ型: string | cell

`ResponseName` — 応答変数の名前
文字ベクトル | string 配列 | 文字ベクトルの cell 配列

応答変数の名前。文字ベクトル、string 配列、または文字ベクトルの cell 配列として指定します。

Y を指定する場合、ResponseName を使用して応答変数の名前を指定できます。
ResponseVarName または formula を指定した場合、ResponseName を使用できません。

例: ResponseName="Response"

例: ResponseName=["Response1","Response2"]

データ型: char | string | cell

`ResponseTransform` — 生の応答値を変換するための関数
`"none"` (既定値) | 関数ハンドル | 関数名

生の応答値を変換するための関数。関数ハンドルまたは関数名として指定します。既定の設定は "none" です。これは @(y)y、つまり変換なしを表します。関数は、元の応答値を受け入れて同じサイズの出力 (変換した応答値) を返さなければなりません。

例: myfunction = @(y)exp(y) を使用して、指数変換を入力ベクトルに適用する関数のハンドルを作成するとします。この場合、応答変換として ResponseTransform=myfunction を指定できます。

データ型: char | string | function_handle

`Weights` — 観測値の重み
非負の数値ベクトル | `Tbl` 内の変数の名前

観測値の重み。非負の数値ベクトルまたは Tbl 内の変数の名前を指定します。ソフトウェアは、X または Tbl の各観測値に、Weights の対応する値で重みを付けます。Weights の長さは、X または Tbl の観測値の数と等しくなければなりません。

入力データを table Tbl として指定した場合、Weights は数値ベクトルが含まれている Tbl 内の変数の名前にすることができます。この場合、Weights には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、重みベクトル W が Tbl.W として格納されている場合、"W" として指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は W を含めてすべて予測子として扱われます。

既定の設定では、Weights は ones(n,1) です。n は X または Tbl の観測値数です。

fitrnet は合計が 1 になるように重みを正規化します。

Inf の重みはサポートされません。Network 引数を使用してニューラルネットワークアーキテクチャを指定する場合、Weights は 1 のベクトルでなければなりません。

データ型: single | double | char | string

交差検証オプション

`CrossVal` — 交差検証済みモデルに学習させるためのフラグ
`"off"` (既定値) | `"on"`

交差検証済みモデルに学習させるためのフラグ。"on" または "off" として指定します。

"on" を指定すると、10 の分割を使用して交差検証済みモデルの学習が実行されます。

名前と値の引数 CVPartition、Holdout、KFold、または Leaveout を使用すると、この交差検証の設定をオーバーライドできます。交差検証済みモデルを作成するときに使用できる交差検証の名前と値の引数は、一度に 1 つだけです。

または、後で Mdl を crossval に渡して交差検証を実行します。

例: Crossval="on"

データ型: char | string

`CVPartition` — 交差検証分割
`[]` (既定値) | `cvpartition` オブジェクト

交差検証分割。交差検証のタイプと学習セットおよび検証セットのインデックス付けを指定する cvpartition オブジェクトとして指定します。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: cvp = cvpartition(500,KFold=5) を使用して、500 個の観測値に対する 5 分割交差検証について無作為な分割を作成するとします。この場合、CVPartition=cvp を設定して交差検証分割を指定できます。

`Holdout` — ホールドアウト検証の対象データの比率
(0,1) の範囲のスカラー値

ホールドアウト検証に使用するデータの比率。範囲 (0,1) のスカラー値として指定します。Holdout=p を指定した場合、以下の手順が実行されます。

p*100% のデータを無作為に選択して検証データとして確保し、残りのデータを使用してモデルに学習をさせる。
コンパクトな学習済みモデルを交差検証済みモデルの Trained プロパティに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: Holdout=0.1

データ型: double | single

`KFold` — 分割の数
`10` (既定値) | 1 より大きい正の整数値

交差検証済みモデルで使用する分割の数。1 より大きい正の整数値として指定します。KFold=k を指定した場合、以下の手順が実行されます。

データを無作為に k 個のセットに分割する。
各セットについて、そのセットを検証データとして確保し、他の k – 1 個のセットを使用してモデルに学習をさせる。
k 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている k 行 1 列の cell ベクトルに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: KFold=5

データ型: single | double

`Leaveout` — Leave-one-out 法の交差検証のフラグ
`"off"` (既定値) | `"on"`

Leave-one-out 法の交差検証のフラグ。"on" または "off" として指定します。Leaveout="on" を指定した場合、n 個の観測値 (n は、モデルの NumObservations プロパティで指定される、欠損観測値を除外した観測値の個数) のそれぞれについて以下の手順が実行されます。

いずれかの観測値を検証データとして確保し、他の n - 1 個の観測値を使用してモデルに学習をさせる。
n 個のコンパクトな学習済みモデルを、交差検証済みモデルの Trained プロパティに含まれている n 行 1 列の cell ベクトルに格納する。

交差検証済みモデルの作成で指定できる名前と値の引数は、CVPartition、Holdout、KFold、Leaveout の 4 つのうちのいずれかのみです。

例: Leaveout="on"

データ型: char | string

メモ

交差検証の名前と値の引数は、名前と値の引数 OptimizeHyperparameters と一緒には使用できません。OptimizeHyperparameters の場合の交差検証は、名前と値の引数 HyperparameterOptimizationOptions を使用することのみによって変更できます。
交差検証のオプションは、多重応答回帰ではサポートされません。

ハイパーパラメーター最適化オプション

`OptimizeHyperparameters` — 最適化するパラメーター
`"none"` (既定値) | `"auto"` | `"all"` | 使用可能パラメーター名の string 配列または cell 配列 | `optimizableVariable` オブジェクトのベクトル

最適化するパラメーター。次のいずれかを指定します。

"none" — 最適化を行いません。
"auto" — ["Activations","Lambda","LayerSizes","Standardize"] を使用します。
"all" — すべての使用可能パラメーターを最適化します。
使用可能パラメーター名の string 配列または cell 配列。
optimizableVariable オブジェクトのベクトル。通常は hyperparameters の出力です。

最適化では、パラメーターを変化させることにより、fitrnet の交差検証損失 (誤差) を最小化しようとします。交差検証のタイプおよびその他の最適化の側面を制御するには、名前と値の引数 HyperparameterOptimizationOptions を使用します。HyperparameterOptimizationOptions を使用すると、ConstraintType オプションと ConstraintBounds オプションを設定することにより、交差検証損失の代わりに (コンパクトな) モデルサイズを最適化の目的として使用できます。

メモ

OptimizeHyperparameters の値は、他の名前と値の引数を使用して指定した値より優先されます。たとえば、OptimizeHyperparameters を "auto" に設定すると、fitrnet は "auto" オプションに対応するハイパーパラメーターを最適化して、ハイパーパラメーターに指定された値を無視します。

モデルのハイパーパラメーターを最適化するには、Network 引数は [] でなければなりません。fitrnet では、以下のパラメーターを使用できます。

Activations — fitrnet は集合 ["relu","tanh","sigmoid","none"] に対して Activations を最適化します。
Lambda — fitrnet は範囲 [1e-5,1e5]/NumObservations の連続値に対して Lambda を最適化します。値は対数変換された範囲内で一様に選択されます。
LayerBiasesInitializer — fitrnet は 2 つの値 ["zeros","ones"] に対して LayerBiasesInitializer を最適化します。
LayerWeightsInitializer — fitrnet は 2 つの値 ["glorot","he"] に対して LayerWeightsInitializer を最適化します。
LayerSizes — fitrnet は、3 つの値 1、2、および 3 に対して、最終全結合層を除く全結合層を最適化します。fitrnet は、対数スケールで標本抽出された 1 ～ 300 の層のサイズに対して、各全結合層を個別に最適化します。
メモ
LayerSizes 引数を使用する場合、反復表示には関連する各層のサイズが表示されます。たとえば、全結合層の現在の数が 3 で、この 3 つの層のサイズがそれぞれ 10、79、44 である場合、反復表示にはこの反復の LayerSizes が [10 79 44] として表示されます。
メモ
5 つの全結合層、または層の異なる範囲のサイズにアクセスするには、hyperparameters を使用して最適化可能なパラメーターおよび範囲を選択します。
Standardize — fitrnet は 2 つの値 [true,false] に対して Standardize を最適化します。

既定以外のパラメーターを設定するには、既定以外の値が含まれている optimizableVariable オブジェクトのベクトルを渡します。例として、次のコードは NumLayers の範囲を [1 5] に設定し、Layer_4_Size および Layer_5_Size を最適化します。

load carsmall
params = hyperparameters("fitrnet",[Horsepower,Weight],MPG);
params(1).Range = [1 5];
params(10).Optimize = true;
params(11).Optimize = true;

OptimizeHyperparameters の値として params を渡します。例については、ニューラルネットワークのカスタムハイパーパラメーターの最適化を参照してください。

既定では、コマンドラインに反復表示が表示され、最適化のハイパーパラメーターの個数に従ってプロットが表示されます。最適化とプロットにおける目的関数は、log(1 + cross-validation loss) です。反復表示を制御するには、名前と値の引数 HyperparameterOptimizationOptions の Verbose オプションを設定します。プロットを制御するには、名前と値の引数 HyperparameterOptimizationOptions の ShowPlots オプションを設定します。

例については、ニューラルネットワークの交差検証誤差の最小化を参照してください。

例: OptimizeHyperparameters="auto"

`HyperparameterOptimizationOptions` — 最適化のオプション
`HyperparameterOptimizationOptions` オブジェクト | 構造体

最適化のオプション。HyperparameterOptimizationOptions オブジェクトまたは構造体として指定します。この引数を指定すると、名前と値の引数 OptimizeHyperparameters の効果が変化します。HyperparameterOptimizationOptions を指定する場合、OptimizeHyperparameters も指定しなければなりません。オプションはいずれも任意です。ただし、AggregateOptimizationResults を返すには ConstraintBounds と ConstraintType を設定しなければなりません。構造体で設定できるオプションは HyperparameterOptimizationOptions オブジェクトと同じです。

オプション	値	既定の設定
`Optimizer`	`"bayesopt"` — ベイズ最適化を使用。内部的には `bayesopt` が呼び出されます。 `"gridsearch"` — 次元ごとに `NumGridDivisions` の値があるグリッド探索を使用。`"gridsearch"` では、グリッドからの一様な非復元抽出により、無作為な順序で探索します。最適化後、`sortrows(Mdl.HyperparameterOptimizationResults)` コマンドを使用してグリッド順の table を取得できます。 `"randomsearch"` — `MaxObjectiveEvaluations` 個の点で無作為に探索。	`"bayesopt"`
`ConstraintBounds`	N 個の最適化問題の制約範囲。N 行 2 列の数値行列または `[]` として指定します。`ConstraintBounds` の列には最適化問題の下限と上限の値が含まれます。`ConstraintBounds` を数値ベクトルとして指定すると、`ConstraintBounds` の 2 列目に値が代入され、1 列目にはゼロが代入されます。`ConstraintBounds` を指定する場合、`ConstraintType` も指定しなければなりません。	`[]`
`ConstraintTarget`	最適化問題の制約ターゲット。`"matlab"` または `"coder"` として指定します。`ConstraintBounds` と `ConstraintType` が `[]` の場合に `ConstraintTarget` を設定すると、`ConstraintTarget` は `[]` に設定されます。`ConstraintTarget` と `ConstraintType` の値により、目的関数と制約関数が決まります。詳細については、`HyperparameterOptimizationOptions` を参照してください。	`ConstraintBounds` と `ConstraintType` を指定する場合の既定値は `"matlab"` です。そうでない場合、既定値は `[]` となります。
`ConstraintType`	最適化問題の制約タイプ。`"size"` または `"loss"` として指定します。`ConstraintType` を指定する場合、`ConstraintBounds` も指定しなければなりません。`ConstraintTarget` と `ConstraintType` の値により、目的関数と制約関数が決まります。詳細については、`HyperparameterOptimizationOptions` を参照してください。	`[]`
`AcquisitionFunctionName`	獲得関数のタイプ: `"expected-improvement-per-second-plus"` `"expected-improvement"` `"expected-improvement-plus"` `"expected-improvement-per-second"` `"lower-confidence-bound"` `"probability-of-improvement"` 目的関数の実行時に最適化が決まるので、名前に `per-second` が含まれている獲得関数は、再現性がある結果を生成しません。名前に `plus` が含まれている獲得関数は、領域を過剰利用している場合に動作を変更します。詳細は、獲得関数のタイプを参照してください。	`"expected-improvement-per-second-plus"`
`MaxObjectiveEvaluations`	目的関数評価の最大数。`ConstraintBounds` を使用して最適化問題を複数指定する場合、`MaxObjectiveEvaluations` の値は各最適化問題に個別に適用されます。	`"bayesopt"` および `"randomsearch"` の場合は `30`、`"gridsearch"` の場合はグリッド全体
`MaxTime`	最適化の制限時間。非負の実数スカラーとして指定します。制限時間の単位は、`tic` と `toc` によって測定される秒です。`MaxTime` の値にかかわらず、少なくとも 1 回は最適化反復が実行されます。`MaxTime` は関数評価を中断させないため、実行時間が `MaxTime` を超える可能性があります。`ConstraintBounds` を使用して最適化問題を複数指定する場合、制限時間は各最適化問題に個別に適用されます。	`Inf`
`NumGridDivisions`	`Optimizer="gridsearch"` における各次元の値の個数。値は、各次元の値の個数を表す正の整数のベクトル、またはすべての次元に適用されるスカラーが可能です。カテゴリカル変数の場合、このオプションは無視されます。	`10`
`ShowPlots`	最適化の進行状況のプロットを表示するかどうかを示す logical 値。このオプションが `true` の場合、最適な観測された目的関数値が反復回数に対してプロットされます。ベイズ最適化を使用する場合 (`Optimizer="bayesopt"`)、最適な推定された目的関数値もプロットされます。最適な観測された目的関数値および最適な推定された目的関数値は、反復表示の `BestSoFar (observed)` 列および `BestSoFar (estim.)` 列の値にそれぞれ対応しています。これらの値は、`Mdl.HyperparameterOptimizationResults` のプロパティ `ObjectiveMinimumTrace` および `EstimatedObjectiveMinimumTrace` で確認できます。問題にベイズ最適化の最適化パラメーターが 1 つまたは 2 つある場合、`ShowPlots` はパラメーターに対する目的関数のモデルもプロットします。	`true`
`SaveIntermediateResults`	最適化の結果を保存するかどうかを示す logical 値。このオプションが `true` の場合、`"BayesoptResults"` という名前のワークスペース変数が反復ごとに上書きされます。この変数は `BayesianOptimization` オブジェクトです。`ConstraintBounds` を使用して最適化問題を複数指定する場合、ワークスペース変数は `"AggregateBayesoptResults"` という名前の `AggregateBayesianOptimization` オブジェクトになります。	`false`
`Verbose`	コマンドラインにおける表示レベル: `0` — 反復表示なし `1` — 反復表示あり `2` — 反復表示と追加情報詳細については、`bayesopt` の名前と値の引数 `Verbose` およびベイズ最適化の使用による分類器の当てはめの最適化の例を参照してください。	`1`
`UseParallel`	ベイズ最適化を並列実行するかどうかを示す logical 値。並列実行には Parallel Computing Toolbox™ が必要です。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。詳細については、並列ベイズ最適化を参照してください。	`false`
`Repartition`	反復ごとに交差検証を再分割するかどうかを示す論理値。このオプションが `false` の場合、オプティマイザーは単一の分割を最適化に使用します。分割ノイズが考慮されるので、通常は値を `true` にすると最も確実な結果が得られます。ただし、`true` で最適な結果を得るには、2 倍以上の関数評価が必要になります。	`false`
次の 3 つのオプションのいずれか 1 つのみを指定してください。
`CVPartition`	`cvpartition` によって作成された `cvpartition` オブジェクト	交差検証オプションが指定されていない場合は `KFold=5`
`Holdout`	ホールドアウトの比率を表す範囲 `(0,1)` のスカラー
`KFold`	1 より大きい整数

例: HyperparameterOptimizationOptions=struct(UseParallel=true)

メモ

ハイパーパラメーター最適化のオプションは、多重応答回帰ではサポートされません。

出力引数

`Mdl` — 学習させたニューラルネットワーク回帰モデル
`RegressionNeuralNetwork` モデルオブジェクト | `RegressionPartitionedNeuralNetwork` モデルオブジェクト

学習させたニューラルネットワーク回帰モデル。RegressionNeuralNetwork モデルオブジェクトまたは RegressionPartitionedNeuralNetwork モデルオブジェクトとして返されます。

名前と値の引数 CrossVal、CVPartition、Holdout、KFold、Leaveout のいずれかを設定した場合、Mdl は RegressionPartitionedNeuralNetwork モデルオブジェクトになります。それ以外の場合、Mdl は RegressionNeuralNetwork モデルオブジェクトになります。

Mdl のプロパティを参照するには、ドット表記を使用します。

OptimizeHyperparameters を指定して HyperparameterOptimizationOptions の ConstraintType オプションと ConstraintBounds オプションを設定している場合、Mdl はモデルオブジェクトの N 行 1 列の cell 配列になります。ここで、N は ConstraintBounds の行数と等しくなります。いずれの最適化問題からも実行可能なモデルが得られない場合、cell 配列の各値が [] になります。

Network 引数を層配列または dlnetwork オブジェクトに設定してモデルを当てはめる場合、モデルのニューラルネットワークアーキテクチャを調べるには、dlnetwork (Deep Learning Toolbox) 関数を使用してモデルを dlnetwork オブジェクトに変換します。

`AggregateOptimizationResults` — 最適化の結果の集計
`AggregateBayesianOptimization` オブジェクト

複数の最適化問題についての最適化の結果の集計。AggregateBayesianOptimization オブジェクトとして返されます。AggregateOptimizationResults を返すには、OptimizeHyperparameters と HyperparameterOptimizationOptions を指定しなければなりません。HyperparameterOptimizationOptions の ConstraintType オプションと ConstraintBounds オプションも指定する必要があります。この出力の生成方法を示す例については、Hyperparameter Optimization with Multiple Constraint Boundsを参照してください。

詳細

ニューラルネットワークの構造

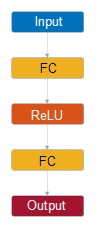
既定のニューラルネットワーク回帰モデルの層構造は次のとおりです。

構造	説明
	入力 — この層は `Tbl` または `X` の予測子データに対応します。
	最初の全結合層 — この層の出力数は既定では 10 です。名前と値の引数 `LayerSizes` を指定して、この層を大きくしたり、全結合層をネットワークにさらに追加したりできます。この層の重みとバイアスは、`Mdl` の `Mdl.LayerWeights{1}` プロパティと `Mdl.LayerBiases{1}` プロパティでそれぞれ確認できます。
	ReLU 活性化関数 — この活性化関数は `fitrnet` で最初の全結合層に適用されます。活性化関数は、名前と値の引数 `Activations` を指定して変更できます。
	最終全結合層 — この層の出力は応答変数ごとに 1 つです。この層の重みとバイアスは、`Mdl` の `Mdl.LayerWeights{end}` プロパティと `Mdl.LayerBiases{end}` プロパティでそれぞれ確認できます。
	出力 — この層は予測応答値に対応します。

この層構造の回帰ニューラルネットワークモデルで予測を返す例については、回帰ニューラルネットワークモデルの層の構造を使用した予測を参照してください。

カスタムのニューラルネットワークアーキテクチャを指定するには、Network 引数を使用します。 (R2025a 以降)

ヒント

数値予測子は可能であれば常に標準化します (Standardize を参照)。標準化を行うと、予測子を測定するスケールの影響を受けなくなります。
モデルに学習をさせた後で、新しいデータについて応答を予測する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。

アルゴリズム

学習ソルバー

fitrnet では、メモリ制限 Broyden-Fletcher-Goldfarb-Shanno 準ニュートンアルゴリズム (LBFGS) [3]が損失関数の最小化手法として使用され、平均二乗誤差 (MSE) が最小化されます。LBFGS ソルバーでは、近似による標準的な直線探索法をヘッシアンに対して使用します。

参照

[1] Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” In Proceedings of the thirteenth international conference on artificial intelligence and statistics, pp. 249–256. 2010.

[2] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification.” In Proceedings of the IEEE international conference on computer vision, pp. 1026–1034. 2015.

[3] Nocedal, J. and S. J. Wright. Numerical Optimization, 2nd ed., New York: Springer, 2006.

拡張機能

自動並列サポート
Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

ハイパーパラメーターの最適化を並列実行するには、fitrnet 関数を呼び出すときに名前と値の引数 HyperparameterOptimizationOptions で UseParallel=true オプションを使用します。

並列的なハイパーパラメーターの最適化の詳細については、並列ベイズ最適化を参照してください。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。 (R2024b 以降)

fitrnet は、次の少なくとも 1 つに該当する場合に GPU でモデルを当てはめます。
- 入力引数 X が gpuArray オブジェクトである。
- 入力引数 Y が gpuArray オブジェクトである。
- 入力引数 Tbl に gpuArray の予測子変数または応答変数が含まれている。

詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2021a で導入