このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
Discrete-Time Integrator
信号の離散時間積分または累積の実行
ライブラリ:
Simulink /
Commonly Used Blocks
Simulink /
Discrete
HDL Coder /
Discrete
HDL Coder /
HDL Floating Point Operations
説明
Discrete-Time Integrator ブロックを Integrator ブロックの代わりに使用して、純粋な離散モデルを作成します。Discrete-Time Integrator ブロックを使用すると、以下のことが可能です。
初期条件をブロック ダイアログ ボックスまたはブロックへの入力で定義する
入力ゲイン (K) の値を定義する
ブロックの状態を出力する
積分の上限と下限を定義します。
追加リセット入力を使用した状態のリセット
出力方程式
最初のタイム ステップでは、ブロックの状態は n = 0 であり、[初期条件設定] パラメーターの値に応じて、初期出力 y(0) = IC または初期状態 x(0) = IC のどちらかです。
シミュレーション時間 t(n) のステップ n > 0 では、Simulink® は出力 y(n) を以下のように更新します。
前進オイラー法:
y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n-1)
後退オイラー法:
y(n) = y(n-1) + K*[t(n) - t(n-1)]*u(n)
台形法:
y(n) = y(n-1) + K*[t(n)-t(n-1)]*[u(n)+u(n-1)]/2
Simulink はブロックの明示的なサンプル時間またはトリガーのサンプル時間に応じて、これらの出力方程式の状態空間表現を自動的に選択します。明示的なサンプル時間を使用する場合、n > 0 のとき、t(n)-t(n-1) はサンプル時間 T に減少します。
積分および累積方法
このブロックは、前進オイラー法、後退オイラー法または台形則を使用して積分または累積を行うことができます。ここで、u は入力、y は出力、x は状態です。Simulink は、与えられたステップ n に対して、y(n) と x(n+1) を更新します。積分モードでは、T はブロックのサンプル時間 (トリガー付きサンプル時間の場合は T の差分) です。累積モードでは T = 1 です。ブロックのサンプル時間は出力が計算されるタイミングを決めますが、出力の値は決めません。K はゲイン値です。出力値は上限値または下限値に従って制限されます。
前進オイラー法 (既定の設定) は、前進矩形近似または左側近似とも呼ばれます。
1/s は T/(z-1) で近似されます。ステップ n でのブロックの出力の式は次のようになります。
x(n+1) = x(n) + K*T*u(n) y(n) = x(n)
ブロックは以下のステップで出力を計算します。
Step 0: y(0) = IC (clip if necessary)
x(1) = y(0) + K*T*u(0)
Step 1: y(1) = x(1)
x(2) = x(1) + K*T*u(1)
Step n: y(n) = x(n)
x(n+1) = x(n) + K*T*u(n) (clip if necessary)この手法では、入力端子 1 には直達がありません。
後退オイラー法は、後退矩形近似または右側近似とも呼ばれます。
1/s は T*z/(z-1) で近似されます。これにより、ステップ n でのブロックの出力の式は、次のようになります。
y(n) = y(n-1) + K*T*u(n).
x(n) = y((n)-1) とします。ブロックは以下のステップで出力を計算します。
Triggered Subsystem と Function-call Subsystem のパラメーター [初期条件設定] が
[出力]または[自動]に設定されている場合。Step 0: y(0) = IC (clipped if necessary) x(1) = y(0)Non-Triggered Subsystem のパラメーター [初期条件設定] が
[自動]に設定されている場合。Step 0: x(0) = IC (clipped if necessary) x(1) = y(0) = x(0) + K*T*u(0) Step 1: y(1) = x(1) + K*T*u(1) x(2) = y(1) Step n: y(n) = x(n) + K*T*u(n) x(n+1) = y(n)
この手法では、入力端子 1 には直達があります。
この手法では、1/s は T/2*(z+1)/(z-1) で近似されます。
T が固定の場合 (サンプリング周期に等しい場合)、出力の計算式は次のようになります。
x(n) = y(n-1) + K*T/2*u(n-1) y(n) = x(n) + K*T/2*u(n)
Triggered Subsystem と Function-call Subsystem のパラメーター [初期条件設定] が
[出力]または[自動]に設定されている場合。Step 0: y(0) = IC (clipped if necessary) x(1) = y(0) + K*T/2*u(0)Non-Triggered Subsystem のパラメーター [初期条件設定] が
[自動]に設定されている場合。Step 0: x(0) = IC (clipped if necessary) y(0) = x(0) + K*T/2*u(0) x(1) = y(0) + K*T/2*u(0) Step 1: y(1) = x(1) + K*T/2*u(1) x(2) = y(1) + K*T/2*u(1) Step n: y(n) = x(n) + K*T/2*u(n) x(n+1) = y(n) + K*T/2*u(n)
ここで x(n+1) は次の出力値の最良の推定値です。x(n) と y(n) は等しくないことから、状態と同じではありません。
この手法では、入力端子 1 には直達があります。
T が可変の場合 (たとえばトリガー時間から得られる場合)、ブロックは次のステップを使用して出力を計算します。
Triggered Subsystem と Function-call Subsystem のパラメーター [初期条件設定] が
[出力]または[自動]に設定されている場合。Step 0: y(0) = IC (clipped if necessary) x(1) = y(0)Non-Triggered Subsystem のパラメーター [初期条件設定] が
[自動]に設定されている場合。Step 0: x(0) = IC (clipped if necessary) x(1) = y(0) = x(0) + K*T/2*u(0) Step 1: y(1) = x(1) + K*T/2*(u(1) + u(0)) x(2) = y(1) Step n: y(n) = x(n) + K*T/2*(u(n) + u(n-1)) x(n+1) = y(n)
初期条件の定義
初期条件は、このブロックのダイアログ ボックスでパラメーターとして定義するか、または外部信号から入力できます。
ブロック パラメーターとして初期条件を定義するには、[初期条件のソース] パラメーターを [
内部] と指定し、値を [初期条件] テキスト ボックスに入力します。外部ソースから初期条件を与えるには、[初期条件のソース] パラメーターを [
外部] に設定します。ブロックに追加の入力端子が表示されます。
状態端子を使用する場合
出力端子ではなく状態端子を使用します。
ブロックの出力がリセット端子または初期条件端子を通りブロックにフィードバックされ、代数ループが生じる場合。例については、
sldemo_bounce_two_integratorsモデルを参照してください。条件付き実行サブシステムの 1 つから他のサブシステムに状態を渡したい場合。この場合、タイミングの問題が生じることがあります。例については、クラッチ ロックアップ モデルの作成を参照してください。
これらの問題は、出力端子ではなく状態端子を通して状態を渡すことによって解決できます。Simulink は、出力とはわずかに異なる時間に状態を生成し、これらの問題からモデルを保護します。ブロックの状態を出力するには、[端子状態の表示] チェック ボックスをオンにします。状態端子がブロックの上に表示されます。
積分の制限
出力が一定のレベルを超えないようにするには、[出力を制限する] チェック ボックスをオンにして、対応するテキスト ボックスに制限値を入力します。このようにすると、ブロックは制限付きで積分器として機能します。出力が制限値に達すると、積分動作はオフになり、積分飽和現象を回避します。シミュレーション中、制限値を変更できますが、出力が制限されているかどうかは変更できません。次の表は、ブロックによる出力の決定方法を示しています。
| 積分 | 出力 |
|---|---|
| [飽和の下限] 未満 | 飽和の下限 |
| [飽和の下限] と [飽和の上限] | 積分 |
| [飽和の上限] より大きい | 飽和の上限 |
積分が制限に達したことを示す信号を生成するには、[飽和端子の表示] チェック ボックスをオンにします。新しい飽和端子はブロック出力端子の下に表示されます。
飽和は、次の 3 つの値のいずれかをもちます。
1 は、積分が上限に達していることを示します。
0 は、積分が制限されないことを示します。
-1 は、積分が下限に達していることを示します。
状態のリセット
このブロックは、そのブロックの状態を外部信号に基づいて指定された初期条件にリセットできます。ブロックに状態をリセットさせるには、[外部リセット] パラメーターのいずれかのオプションを選択します。リセット トリガーのタイプを示すリセット端子が表示されます。
リセット端子は直達をもちます。ブロック出力が直達をもつブロックを通じてこの端子にフィードバックされる場合や、直接フィードバックされる場合、代数ループが発生します。このループを解除するには、ブロックの状態端子の出力をリセット端子に接続します。ブロックの状態にアクセスするには、[端子状態の表示] チェック ボックスをオンにします。
トリガー タイプのリセット
[外部リセット] パラメーターによって、リセットをトリガーするリセット信号の属性を決めることができます。トリガー オプションには以下が含まれます。
立ち上がり– リセット信号が立ち上がりエッジをもつ場合、状態をリセットします。たとえば、次の図は立ち上がりリセット トリガーによる後退オイラー積分の効果を示します。
立ち下がり– リセット信号が立ち下がりエッジをもつ場合、状態をリセットします。たとえば、次の図は立ち下がりリセット トリガーによる後退オイラー積分の効果を示します。
両方– リセット信号が立ち上がりまたは立ち下がりをもつ場合、状態をリセットします。たとえば、次の図はいずれかのリセット トリガーによる後方オイラー積分の効果を示します。
レベル– リセット信号が非ゼロである間、出力を初期条件にリセットしてホールドします。たとえば、次の図はレベル リセット トリガーによる後退オイラー積分の効果を示します。
サンプル レベル– リセット信号が非ゼロの場合、出力を初期条件にリセットします。たとえば、次の図はサンプル レベル リセット トリガーによる後退オイラー積分の効果を示します。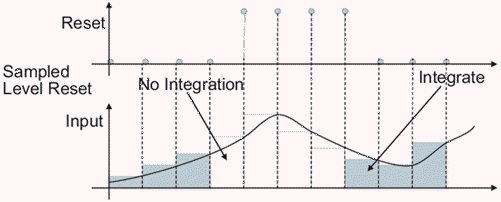
[サンプル レベル]リセット オプションは計算量が少ないため、[レベル]リセット オプションよりも効率的です。メモ
Discrete-Time Integrator ブロックでのトリガーの検出は、いずれも正の値をもつ信号に基づいて行われます。たとえば、-1 から 0 に遷移する信号は立ち上がりエッジと見なされませんが、0 から 1 に遷移する信号は立ち上がりエッジと見なされます。
簡易初期化モードの動作
簡易初期化モードは、[コンフィギュレーション パラメーター] ダイアログで [指定不足の初期化の検出] を [簡易] に設定すると有効になります。簡易初期化モードを使用すると、Discrete-Time Integrator ブロックはクラシック初期化モードとは異なった動作をします。新しい初期化動作はロバスト性が高く、以下の場合は整合性のある動作をします。
代数ループ内
イネーブルとディセーブル時
トリガー サンプル時間を使用した結果と明示的なサンプル時間を比較する場合。なお、ブロックは明示的なサンプル時間と同じレートでトリガーがかかります。
簡易初期化モードを使用すると、Continuous-Time Integrator ブロックを Discrete-Time Integrator ブロックに変換しやすくなります。これは初期条件が両方のブロックで同じ意味をもつためです。
従来の初期化モードと簡易初期化モードの詳細は、Underspecified initialization detectionを参照してください。
Triggered Subsystem と Function-call Subsystem の [初期条件設定] を [出力] に設定して簡易初期化モードを使用する場合、ブロックのイネーブルとディセーブルの動作は以下のように簡略化されます。
ディセーブル時 td:
y(td) = y(td-1)
イネーブル時 te:
親サブシステムの制御端子で [イネーブル時の状態] が
リセットに設定されている場合:y(te) = IC.
親サブシステムの制御端子で [イネーブル時の状態] が
保持に設定されている場合:y(te) = y(td).
次の図は、この条件を示しています。
簡易初期化モードを使用する場合、Discrete-Time Integrator ブロックを反復サブシステム内に置くことはできません。
簡易初期化モードでは、反復サブシステムは経過時間を保持しません。そのため、経過時間を必要とする Discrete-Time Integrator ブロックが反復サブシステムブロック内に置かれた場合、Simulink はエラーを報告します。
Function-Call Subsystem 内の Enabled Subsystem での動作
Discrete-Time Integrator ブロックが含まれる Enabled Subsystem を含む Function-Call Subsystem システムがある場合、次の動作が適用されます。
| 積分手法 | 関数呼び出しトリガー端子のサンプル時間タイプ | Function-Call Subsystem をイネーブルにした後に始めて実行するときの delta T | 動作の理由 |
|---|---|---|---|
前進オイラー法 | トリガー |
| Function-Call Subsystem を最初に実行するとき、積分アルゴリズムは |
後退オイラー法および台形則 | トリガー |
| Function-Call Subsystem を最初に実行するとき、積分アルゴリズムは |
前進オイラー法、後退オイラー法、および台形則 | 周期的 | 関数呼び出しジェネレーターのサンプル時間 | 周期モードでは、Discrete-Time Integrator ブロックは、 |
例
前進オイラー積分法を使用した離散時間積分
モデル sldemo_fuelsys ではサブシステム fuel_rate_control/airflow_calc の Discrete-Time Integrator ブロックを使用します。
クラッチ ロックアップ モデルの作成
この例では、Simulink® を使用して回転クラッチ システムをモデル化およびシミュレーションする方法を示します。ロックアップ時にシステム ダイナミクスにおいてトポロジーが変化するため、クラッチ システムのモデル化は困難ですが、この例題では、Enabled Subsystem がこのような問題をいかに簡単に処理できるかを示します。クラッチ シミュレーションの作成において重要な Simulink モデル化概念を採用する方法を説明します。設計者は、動的に変化する可能性がある強い不連続性と制約を伴う多くのモデルにこうした概念を適用できます。
跳ねるボールのシミュレーション
この例では、跳ねるボールの 2 つのモデルを使用して、Zeno 動作があるハイブリッド動的システムをモデル化する異なるアプローチを示します。Zeno 動作の簡略的な特徴として、特定の複合システムに対して一定の時間間隔で無限個のイベントが発生することが挙げられます。ボールがエネルギーを失うにつれ、連続したより短い時間間隔で地面と衝突するようになります。
端子
入力
出力
パラメーター
ブロックの特性
データ型 |
|
直達 |
|
多次元信号 |
|
可変サイズの信号 |
|
ゼロクロッシング検出 |
|
拡張機能
バージョン履歴
R2006a より前に導入
参考
トピック
- C Data Code Interface Configuration for Model Interface Elements (Simulink Coder)
- C Data Code Interface Configuration for Model Interface Elements (Simulink Coder)
- Struct ストレージ クラスを使用してパラメーター データを構造体に整理する (Embedded Coder)
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)