findpeaks

局所的最大値

ページ内をすべて折りたたむ

構文

pks = findpeaks(y)

[pks,locs] = findpeaks(y)

[pks,locs,w,p] = findpeaks(y)

[___] = findpeaks(y,x)

[___] = findpeaks(y,Fs)

[___] = findpeaks(___,Name,Value)

findpeaks(___)

説明

pks = findpeaks(y) は、入力信号ベクトル y から局所的最大値 (ピーク) をもつベクトルを返します。"局所的なピーク" は、2 つの隣接するサンプルよりも大きいか、Inf と等しいデータサンプルです。ピークは発生順に出力されます。Inf でない信号の端点は除外されます。ピークが平坦である場合、関数は最小のインデックスをもつ点のみを返します。

例

[pks,locs] = findpeaks(y) はさらに、ピークが発生するインデックスを返します。

例

[pks,locs,w,p] = findpeaks(y) は、さらにベクトル w としてピーク幅を、ベクトル p としてピークのプロミネンスを返します。

例

[___] = findpeaks(y,x) は x を位置ベクトルとして指定し、前の構文の出力引数のいずれかを返します。locs および w はx で表されます。

例

[___] = findpeaks(y,Fs) は、データのサンプルレート Fs を指定します。y の最初のサンプルは時間ゼロでとられたものと想定されます。locs および w は時間の単位に変換されます。

例

[___] = findpeaks(___,Name,Value) は、前の構文の入力引数に加えて、名前と値の引数を使用してオプションを指定します。

例

出力引数を指定しない findpeaks(___) は信号をプロットし、ピーク値を重ね合わせます。

例

すべて折りたたむ

ベクトルにおけるピークを検出します。

ライブスクリプトを開く

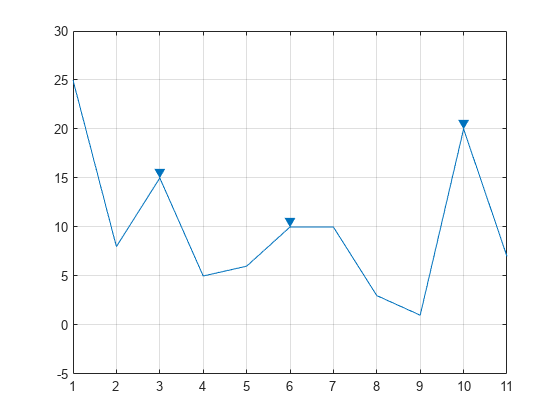
3 つのピークをもつベクトルを定義し、プロットします。

data = [25 8 15 5 6 10 10 3 1 20 7];
plot(data)

Figure contains an axes object. The axes object contains an object of type line.

局所的最大値を求めます。ピークは発生順に出力されます。最初のサンプルは最大であっても含まれません。平坦なピークの場合、関数は最も低いインデックスをもつ点のみを返します。

pks = findpeaks(data)

pks = 1×3

    15    10    20

出力引数なしで findpeaks を使用してピークを表示します。

findpeaks(data)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

ピークとその位置の検索

ライブスクリプトを開く

ベル型曲線の和を構成する信号を作成します。各曲線の位置、高さ、幅を指定します。

x = linspace(0,1,1000);

Pos = [1 2 3 5 7 8]/10;
Hgt = [3 4 4 2 2 3];
Wdt = [2 6 3 3 4 6]/100;

for n = 1:length(Pos)
    Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2);
end

PeakSig = sum(Gauss);

個々の曲線とその和をプロットします。

plot(x,Gauss,'--',x,PeakSig)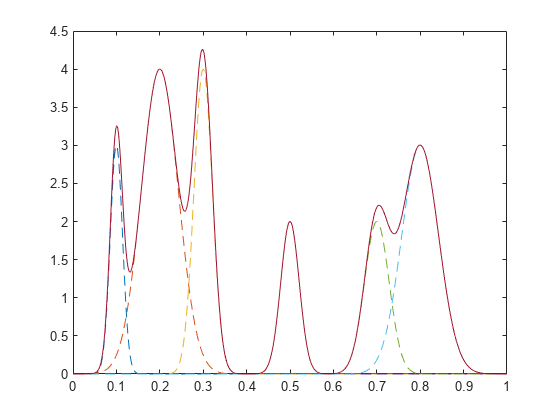

Figure contains an axes object. The axes object contains 7 objects of type line.

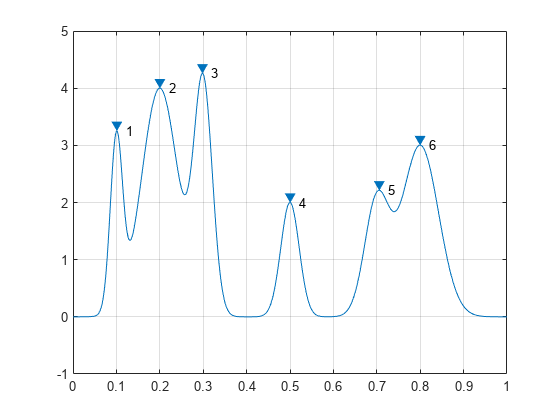
既定の設定で findpeaks を使用して信号のピークとそれらの位置を求めます。

[pks,locs] = findpeaks(PeakSig,x);

findpeaks を使用してピークをプロットし、それにラベルを付けます。

findpeaks(PeakSig,x)

text(locs+.02,pks,num2str((1:numel(pks))'))

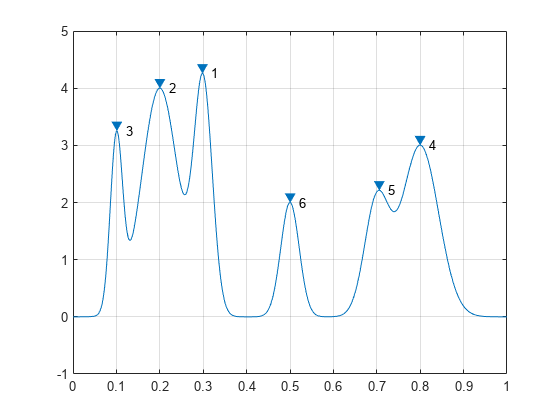
Figure contains an axes object. The axes object contains 8 objects of type line, text. One or more of the lines displays its values using only markers

最も高いピークから低いピークに並べ替えます。

[psor,lsor] = findpeaks(PeakSig,x,'SortStr','descend');

findpeaks(PeakSig,x)

text(lsor+.02,psor,num2str((1:numel(psor))'))

Figure contains an axes object. The axes object contains 8 objects of type line, text. One or more of the lines displays its values using only markers

ピークのプロミネンス

ライブスクリプトを開く

余弦 1 周期の区間を進むベル型曲線の和から構成される信号を作成します。各曲線の位置、高さ、幅を指定します。

x = linspace(0,1,1000);

base = 4*cos(2*pi*x);

Pos = [1 2 3 5 7 8]/10;
Hgt = [3 7 5 5 4 5];
Wdt = [1 3 3 4 2 3]/100;

for n = 1:length(Pos)
    Gauss(n,:) =  Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2);
end

PeakSig = sum(Gauss)+base;

個々の曲線とその和をプロットします。

plot(x,Gauss,'--',x,PeakSig,x,base)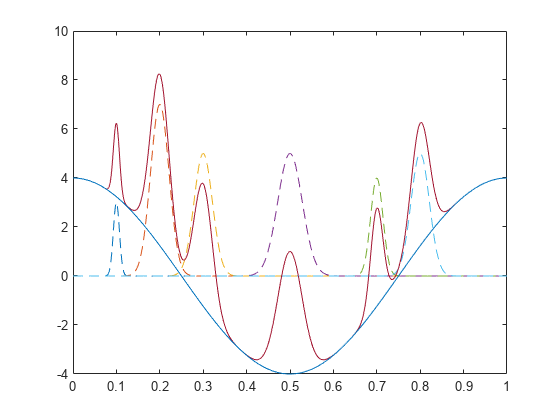

Figure contains an axes object. The axes object contains 8 objects of type line.

findpeaks を使用して 4 以上のプロミネンスをもつピークの場所を特定しプロットします。

findpeaks(PeakSig,x,'MinPeakProminence',4,'Annotate','extents')

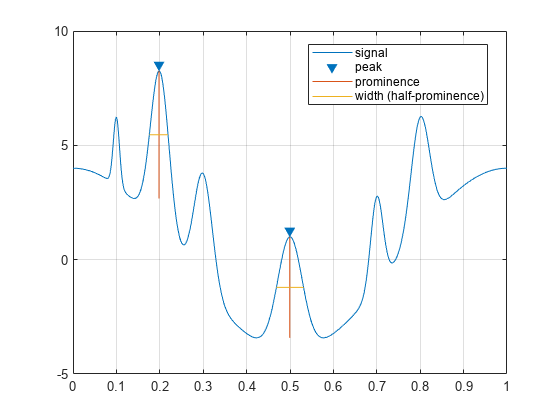
Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent signal, peak, prominence, width (half-prominence).

最も高いピークと最も低いピークだけが条件を満たすピークです。

すべてのピークのプロミネンスおよびプロミネンスの半分の幅を表示します。

[pks,locs,widths,proms] = findpeaks(PeakSig,x);
widths

widths = 1×6

    0.0154    0.0431    0.0377    0.0625    0.0274    0.0409

proms

proms = 1×6

    2.6816    5.5773    3.1448    4.4171    2.9191    3.6363

最小離隔距離のピークの検出

ライブスクリプトを開く

黒点は周期的現象です。その数は、おおよそ 11 年ごとにピークを迎えることが知られています。

sunspot.dat ファイルを読み込みます。このファイルには、1700 年から 1987 年までに観測された太陽黒点数の毎年の平均が含まれています。最大値を求めてプロットします。

load sunspot.dat

year = sunspot(:,1);
avSpots = sunspot(:,2);

findpeaks(avSpots,year)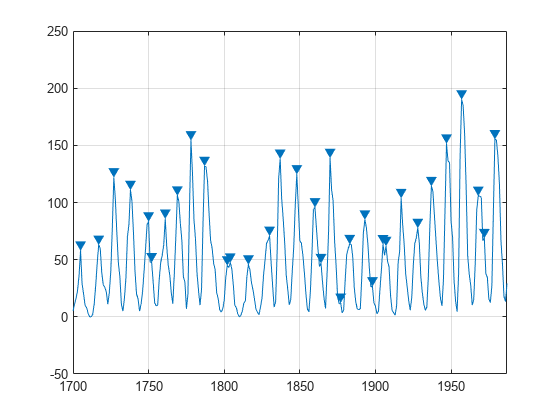

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

サイクル期間の推定は、相互の距離が非常に近いピークを無視することで精度が上がります。再度ピークを求めてプロットしますが、今回は受け入れることができるピークツーピークの離隔距離を 6 年よりも大きな値に制限します。

findpeaks(avSpots,year,'MinPeakDistance',6)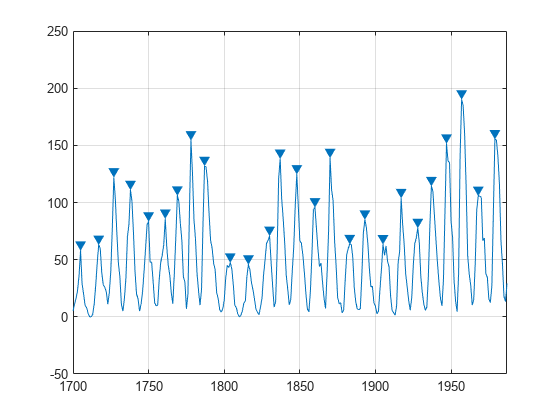

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

findpeaks で返されたピークの位置を使用して最大値間の平均間隔を計算します。

[pks,locs] = findpeaks(avSpots,year,'MinPeakDistance',6);

meanCycle = mean(diff(locs))

meanCycle = 
10.9600

年データを使用して datetime 配列を作成します。黒点は毎年春分近くの 3 月 20 日にカウントされたと仮定します。黒点数がピークとなる年を求めます。関数 years を使用して、最小ピーク離隔距離を duration として指定します。

ty = datetime(year,3,20);

[pk,lk] = findpeaks(avSpots,ty,'MinPeakDistance',years(6));

plot(ty,avSpots,lk,pk,'o')

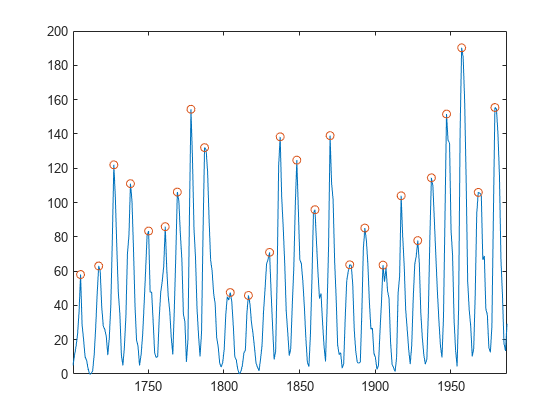
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

datetime の機能を使用して、平均黒点サイクルを計算します。

dttmCycle = years(mean(diff(lk)))

dttmCycle = 
10.9600

データを使用して timetable を作成します。時間変数を年で指定します。データをプロットします。timetable の最後の 5 つのエントリを表示します。

TT = timetable(years(year),avSpots);
plot(TT.Time,TT.Variables)

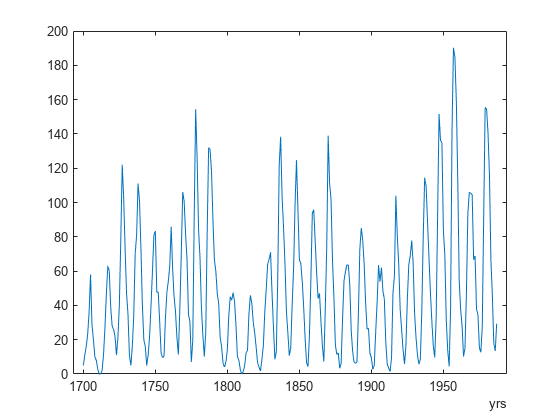
Figure contains an axes object. The axes object contains an object of type line.

entries = TT(end-4:end,:)

entries=5×1 timetable
      Time      avSpots
    ________    _______

    1983 yrs     66.6  
    1984 yrs     45.9  
    1985 yrs     17.9  
    1986 yrs     13.4  
    1987 yrs     29.3

ピーク特性の制約

ライブスクリプトを開く

7418 Hz でサンプリングされた音声信号を読み込みます。200 サンプルを選択します。

load mtlb
select = mtlb(1001:1200);

最小分離間隔 5 ms でピークを検出します。

この制約を適用するため、findpeaks は信号の最も高いピークを選択し、5 ms 以内のすべてのピークを排除します。次に、関数は残りのピークの中で最も高いピークを選択するためにこの手順を繰り返し、考慮すべきピークがなくなるまで反復します。

findpeaks(select,Fs,'MinPeakDistance',0.005)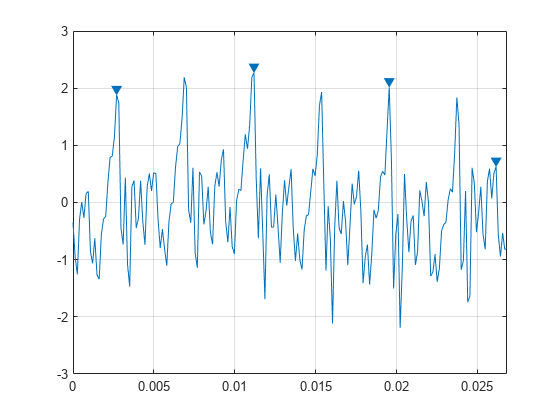

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

1 V 以上の振幅をもつピークを検出します。

findpeaks(select,Fs,'MinPeakHeight',1)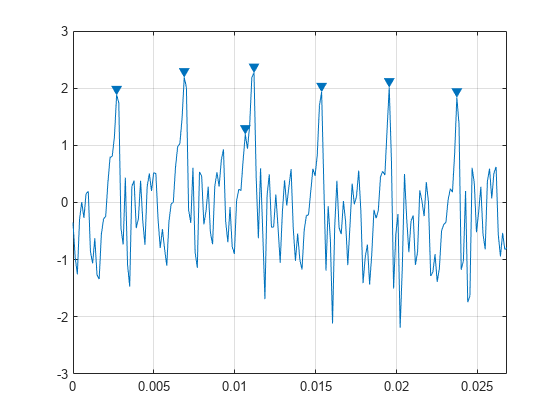

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

隣接するサンプルよりも 1 V 以上高いピークを検出します。

findpeaks(select,Fs,'Threshold',1)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

より高い値に信号が達する前にいずれかの側に 1 V 以上ドロップしているピークを検出します。

findpeaks(select,Fs,'MinPeakProminence',1)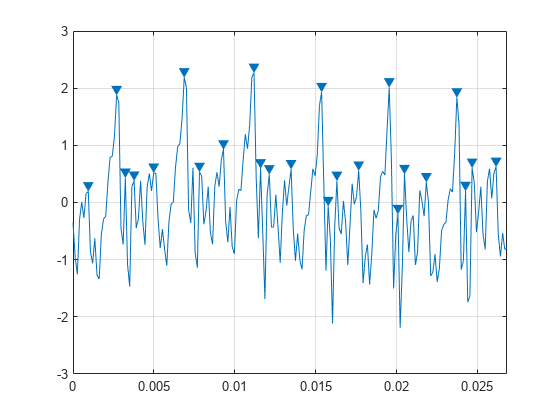

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

飽和した信号のピーク

ライブスクリプトを開く

データが指定した飽和点より大きい場合、センサーはクリップした読み取り値を返します。これらのピークを無意味なものとして無視するか、あるいは解析に組み込むように選択できます。

分散 0.1² のホワイトガウスノイズに含まれる、周波数が 5 Hz と 3 Hz の三角関数の積で構成された信号を生成します。信号は、100 Hz のレートで 1 秒間サンプリングされます。再現可能な結果が必要な場合は、乱数発生器をリセットします。

rng default

fs = 1e2;
t = 0:1/fs:1-1/fs;

s = sin(2*pi*5*t).*sin(2*pi*3*t)+randn(size(t))/10;

0.32 の指定範囲より大きいすべての読み取り値を切り捨てることで、飽和した測定値をシミュレートします。飽和した信号をプロットします。

bnd = 0.32;
s(s>bnd) = bnd;

plot(t,s)
xlabel('Time (s)')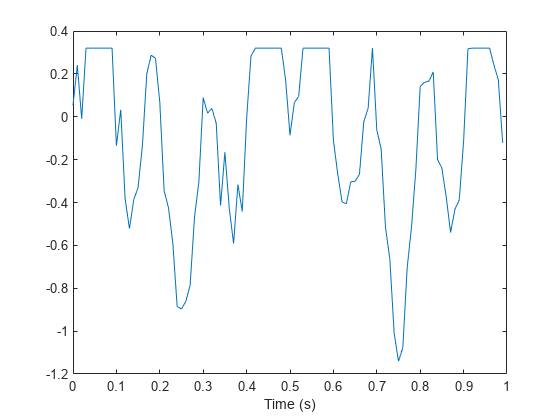

Figure contains an axes object. The axes object with xlabel Time (s) contains an object of type line.

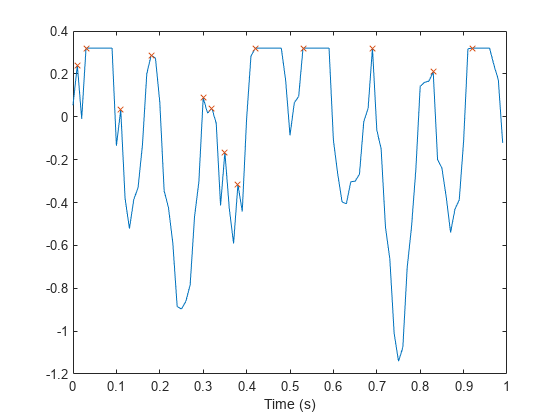
信号のピークの位置を特定します。findpeaks は、平らなピークのそれぞれの立ち上がりエッジのみをレポートします。

[pk,lc] = findpeaks(s,t);

hold on
plot(lc,pk,'x')

Figure contains an axes object. The axes object with xlabel Time (s) contains 2 objects of type line. One or more of the lines displays its values using only markers

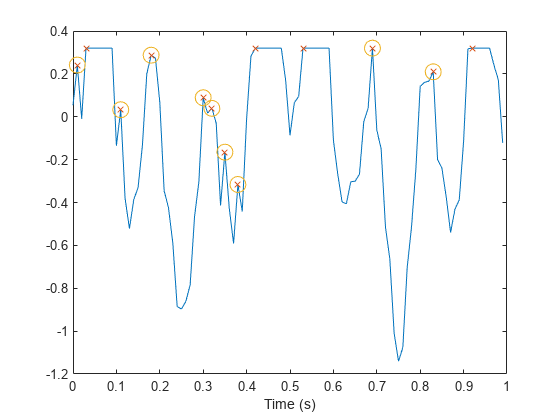
'Threshold' の名前と値のペアを使用して平らなピークを除外します。ピークとその両隣との間には、最小振幅差として $1 0^{- 4}$ が必要です。

[pkt,lct] = findpeaks(s,t,'Threshold',1e-4);

plot(lct,pkt,'o','MarkerSize',12)

Figure contains an axes object. The axes object with xlabel Time (s) contains 3 objects of type line. One or more of the lines displays its values using only markers

ピーク幅の特定

ライブスクリプトを開く

ベル型曲線の和を構成する信号を作成します。各曲線の位置、高さ、幅を指定します。

x = linspace(0,1,1000);

Pos = [1 2 3 5 7 8]/10;
Hgt = [4 4 2 2 2 3];
Wdt = [3 8 4 3 4 6]/100;

for n = 1:length(Pos)
    Gauss(n,:) =  Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2);
end

PeakSig = sum(Gauss);

個々の曲線とその和をプロットします。

plot(x,Gauss,'--',x,PeakSig)
grid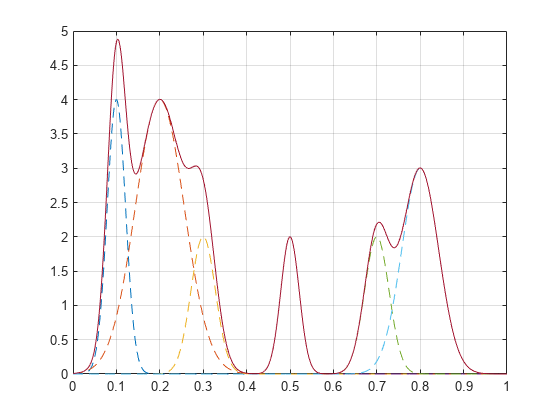

Figure contains an axes object. The axes object contains 7 objects of type line.

プロミネンスの半分を基準として使用してピーク幅を測定します。

findpeaks(PeakSig,x,'Annotate','extents')

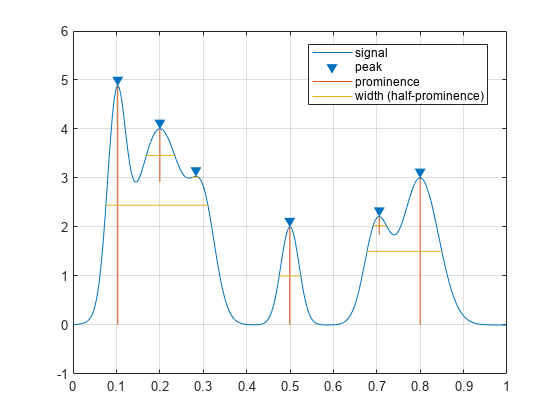
今度は基準として高さの半分を使用して幅を再測定します。

findpeaks(PeakSig,x,'Annotate','extents','WidthReference','halfheight')
title('Signal Peak Widths')

Figure contains an axes object. The axes object with title Signal Peak Widths contains 6 objects of type line. One or more of the lines displays its values using only markers These objects represent signal, peak, height, width (half-height), border.

非線形最小二乗法によるピークの改善

ライブスクリプトを開く

sinc 関数カーネルを使った非線形最小二乗法を使用して、信号内の主要な 2 つのピークの正確なピーク位置推定値を取得します。

信号の生成

線形 FM 波形のレーダーパルス圧縮により、sinc 形状のスペクトルが生成されます。この際、ピーク周波数の位置は、レーダーと検出されたオブジェクトとの間の距離に比例します。まず、findpeaksを使用してピークの位置と振幅を推定し、次に、refinepeaksを使用して推定結果を改善することができます。この例では、合成ノイズレスパルス圧縮信号のピーク振幅と位置を求め、refinepeaks を使用して推定結果を改善します。

それぞれ 4.76 kHz と 35.8 kHz のピークが 1 と 1.5 である 2 つの sinc 形状の波形で構成される信号を生成します。周波数間隔を 2.5 Hz に設定します。

aTarget = [1 1.5];
fTarget = 1e3*[4.76 35.8];
freqkHzFull = (0:0.0025:50)';
waveFull = abs(sinc([1 0.5].*(freqkHzFull-fTarget/1e3)))*aTarget';

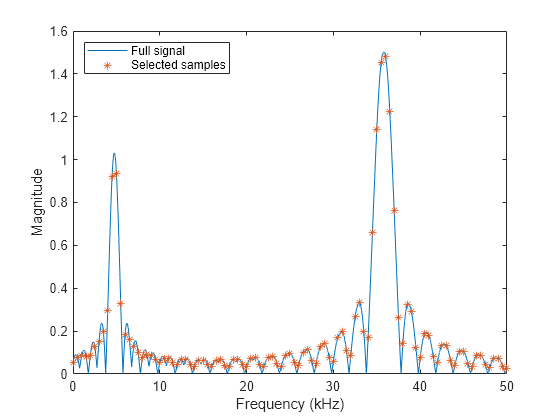
信号を係数 200 でダウンサンプリングし、サンプル間の周波数間隔が 0.5 kHz になるようにします。この例では、ダウンサンプリングされた信号のピークの振幅と位置の推定値を改善し、改善後の推定値を元の信号の値と比較します。

freq = downsample(freqkHzFull,200);
wave = downsample(waveFull,200);

plot(freqkHzFull,waveFull,freq,wave,"*")
legend(["Full signal" "Selected samples"],Location="northwest")
xlabel("Frequency (kHz)")
ylabel("Magnitude")

Figure contains an axes object. The axes object with xlabel Frequency (kHz), ylabel Magnitude contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Full signal, Selected samples.

非線形最小二乗法を使用したピークの改善

findpeaks を使用して、信号に含まれる最も高い 2 つのピークの振幅、位置、および半値幅の初期推定値を求めます。

[PV,PL,PW] = findpeaks(wave,NPeaks=2, ...
    SortStr="descend",WidthReference="halfheight");

refinepeaks を使用して、非線形最小二乗法 (NLS) でピーク推定結果を改善します。信号の周波数点とピーク幅を指定します。ピーク値は予想値の 1.5 と 1 にかなり近く、周波数位置はそれぞれ 35.8 kHz と 4.76 kHz によく近似しています。

LW = max(PW,2);
[Ypk,Xpk] = refinepeaks(wave,PL,freq,Method="NLS",LobeWidth=LW)

Ypk = 2×1

    1.5063
    1.0163

Xpk = 2×1

   35.8001
    4.7628

改善後のピークの振幅を y 軸に、初期ピーク推定値を基準とした更新後のピークの位置を x 軸にプロットします。最初に推定された 2 つのピークとその周囲の 2 つのサンプルは、それぞれ 0.5 kHz ずつ離れています。塗りつぶされた円で示される改善後のピークは、最初に推定されたピーク位置に対する実際のピーク位置と、修正された振幅を示しています。

refinepeaks(wave,PL,freq,Method="NLS",LobeWidth=LW)
yline(aTarget) % Theoretical peak amplitudes
errorBounds = aTarget.*(1+0.03*[-1;1]);
yline(errorBounds(:),":") % ±3% error bounds
legend("Peak "+[1 2])

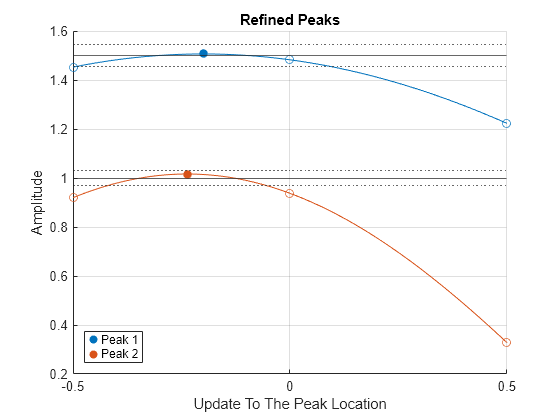
Figure contains an axes object. The axes object with title Refined Peaks, xlabel Update to Peak Location, ylabel Amplitude contains 13 objects of type scatter, line, constantline. These objects represent Peak 1, Peak 2.

入力引数

すべて折りたたむ

`y` — 入力データ
ベクトル

入力データ。ベクトルとして指定します。y は実数で要素数が 3 以上でなければなりません。

データ型: double | single

`x` — 位置
ベクトル | `datetime` 配列

位置。ベクトルまたは datetime 配列として指定します。x は単調増加で y と同じ長さでなければなりません。x を省略した場合、y のインデックスが位置として使用されます。

データ型: double | single | datetime

`Fs` — サンプルレート
正のスカラー

サンプルレート。正のスカラーで指定します。サンプルレートは単位時間あたりのサンプル数です。時間の単位が秒の場合、サンプルレートの単位は Hz です。

データ型: double | single

名前と値の引数

すべて折りたたむ

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: findpeaks(y,x,SortStr="descend",NPeaks=3) では、信号 y の最も高いピークを 3 つ求めます。

`NPeaks` — ピークの最大数
正の整数スカラー

返されるピークの最大数。正の整数スカラーとして指定します。findpeaks は入力データの最初の要素から演算を開始し、ピークの数が 'NPeaks' の値に達すると終了します。

データ型: double | single

`SortStr` — ピークの並べ替え
`'none'` (既定値) | `'ascend'` | `'descend'`

ピークの並べ替え。次のいずれかの値として指定します。

'none' は入力データの発生順でピークを返します。
'ascend' はピークを最小値から最大値への昇順、つまり増加順で返します。
'descend' はピークを最大値から最小値への降順で返します。

`MinPeakHeight` — ピーク高の最小値
`-Inf` (既定値) | 実数スカラー

ピーク高の最小値。実数スカラーとして指定します。この引数を使用して、findpeaks が 'MinPeakHeight' よりも高いピークのみを返すようにします。最小ピーク高を指定することで処理時間が短縮されます。

データ型: double | single

`MinPeakProminence` — 最小ピークのプロミネンス
0 (既定値) | 非負の実数スカラー

最小ピークのプロミネンス。非負の実数スカラーとして指定します。この引数を使用して、findpeaks が少なくとも 'MinPeakProminence' の相対的な重要性をもつピークのみを返すようにします。詳細については、プロミネンスを参照してください。

データ型: double | single

`Threshold` — 最小高さ距離
0 (既定値) | 非負の実数スカラー

ピークとその隣接値との高さの最小差異。非負の実数スカラーとして指定します。findpeaks はこの引数を使用して、隣接値を少なくとも 'Threshold' の値分を上回るピークのみを返します。

データ型: double | single

`MinPeakDistance` — 最小ピーク離隔距離
0 (既定値) | 正の実数のスカラー

最小ピーク離隔距離。正の実数スカラーとして指定します。'MinPeakDistance' に値を指定した場合、アルゴリズムは信号の最も高いピークを選択し、信号の 'MinPeakDistance' 以内のすべてのピークを無視します。次に、関数は残りのピークの中で最も高いピークを選択するためにこの手順を繰り返し、考慮すべきピークがなくなるまで反復します。

位置ベクトル x を指定した場合、'MinPeakDistance' は必ず x で表されます。x が datetime 配列の場合は、'MinPeakDistance' を duration スカラーまたは日単位で表される数値スカラーとして指定します。
サンプルレート Fs を指定した場合、'MinPeakDistance' は必ず時間の単位で表されます。
x と Fs のどちらも指定しない場合、'MinPeakDistance' は必ずサンプルの単位で表されます。

この引数を使用して、findpeaks により大きなピークの近傍で発生する小さなピークを無視させます。

データ型: double | single | duration

`WidthReference` — 幅の測定値の基準の高さ
`'halfprom'` (既定値) | `'halfheight'`

幅の測定値の基準の高さ。'halfprom' または 'halfheight' のいずれかとして指定します。findpeaks は降順の信号が水平の基準線を横切る点の間の距離としてピーク幅を推定します。線の高さは 'WidthReference' で指定されている基準を使用して選択されます。

'halfprom' はピークのプロミネンスの半分に等しい垂直距離にあるピークの下に基準線を配置します。詳細については、プロミネンスを参照してください。
'halfheight' はピーク高さの 1/2 の位置に基準線を配置します。この線は、任意のインターセプトポイントが 'MinPeakHeight'、'MinPeakProminence' および 'Threshold' の設定によって選択されたピークの境界を超えた場合に打ち切られます。ピーク間の境界は、ピーク間の最も低い谷の水平位置で定義されます。高さがゼロ未満のピークは破棄されます。

インターセプトポイントの位置は、線形内挿で計算されます。

`MinPeakWidth` — 最小ピーク幅
0 (既定値) | 正の実数のスカラー

最小ピーク幅。正の実数スカラーとして指定します。この引数を使用して、'MinPeakWidth' 以上の幅をもつピークだけを選択します。

位置ベクトル x を指定した場合、'MinPeakWidth' は必ず x で表されます。x が datetime 配列の場合は、'MinPeakWidth' を duration スカラーまたは日単位で表される数値スカラーとして指定します。
サンプルレート Fs を指定した場合、'MinPeakWidth' は必ず時間の単位で表されます。
x と Fs のどちらも指定しない場合、'MinPeakWidth' は必ずサンプルの単位で表されます。

データ型: double | single | duration

`MaxPeakWidth` — 最大ピーク幅
`Inf` (既定値) | 正の実数のスカラー

最大ピーク幅。正の実数スカラーとして指定します。この引数を使用して、最大 'MaxPeakWidth' の幅をもつピークだけを選択します。

位置ベクトル x を指定した場合、'MaxPeakWidth' は必ず x で表されます。x が datetime 配列の場合は、'MaxPeakWidth' を duration スカラーまたは日単位で表される数値スカラーとして指定します。
サンプルレート Fs を指定した場合、'MaxPeakWidth' は必ず時間の単位で表されます。
x と Fs のどちらも指定しない場合、'MaxPeakWidth' は必ずサンプルの単位で表されます。

データ型: double | single | duration

`Annotate` — プロットのスタイル
`'peaks'` (既定値) | `'extents'`

プロットのスタイル。次のいずれかの値として指定します。

'peaks' は信号をプロットし、各ピークの位置と値の注釈を付けます。
'extents' は信号をプロットし、各ピークの位置、値、幅およびプロミネンスに注釈を付けます。

この引数は出力引数で findpeaks を呼び出している場合に無視されます。

出力引数

すべて折りたたむ

`pks` — 局所的最大値
ベクトル

局所的最大値。信号値のベクトルで返されます。局所的最大値がない場合、pks は空です。

`locs` — ピークの位置
ベクトル

ベクトルとして返されるピークの位置。

位置ベクトル x を指定した場合、locs はピークのインデックスに x の値を含めます。
サンプルレート Fs を指定した場合、locs は連続するサンプル間の時間差が 1/Fs となる時点の数値ベクトルです。
x と Fs のどちらも指定しない場合、locs は整数インデックスのベクトルです。

`w` — ピーク幅
ベクトル

ピーク幅。実数のベクトルとして返します。各ピークの幅は、WidthReference で指定された高さの基準線に信号が交差する、ピークの左右の点の間の距離を計算します。点自体は線形内挿で検出されます。

位置ベクトル x を指定した場合、幅は x で表されます。
サンプルレート Fs を指定した場合、時間の単位で表されます。
x と Fs のどちらも指定しない場合、幅はサンプル単位で表されます。

`p` — ピークのプロミネンス
ベクトル

ピークのプロミネンス。実数のベクトルとして返します。ピークのプロミネンスとは、信号がピークよりも高いレベルに戻るか、端点に到達する前にピークのいずれかの側に信号が下降して到達する必要のある最小垂直距離です。詳細については、プロミネンスを参照してください。

詳細

すべて折りたたむ

プロミネンス

ピークの "プロミネンス" はピークの固有の高さと、他のピークとの相対的な位置によって、そのピークがどの程度突出しているかを測定します。低い位置で孤立しているピークが、より高い位置であってもその周囲から突出していないピークと比べた場合、プロミネンスの度合いがより高くなる場合があります。

ピークのプロミネンスは以下により測定します。

ピーク上にマーカーを配置します。
ピークの水平線を以下のいずれかの状態になるまで左右に伸ばします。
- より高いピークと信号が交差
- 信号の左端または右端への到達
手順 2 で定義した 2 つの区間のそれぞれで信号の最小値を見つけます。このポイントは、谷または信号端点の 1 つのいずれかです。
2 つの区間の最小値の高い方の値が基準レベルを規定します。この基準レベルより上のピーク高がプロミネンスです。

findpeaks は、その信号の両端点を超えた動作については、高さに関係なく仮定を行いません。このため、手順 2 および 4 では信号の両端点を超えた動作が無視され、基準レベルの値に影響を与えることがよくあります。この信号のピークが以下のような場合を考えてみましょう。

ピークの番号	ピークからの左区間の端点	ピークからの右区間の端点	左区間の最低点	右区間の最低点	基準レベル (最高極小)
1	左端	ピーク 2 によるクロッシング	左の端点	a	a
2	左端	右端	左の端点	h	左の端点
3	ピーク 2 によるクロッシング	ピーク 4 によるクロッシング	b	c	c
4	ピーク 2 によるクロッシング	ピーク 6 によるクロッシング	b	d	b
5	ピーク 4 によるクロッシング	ピーク 6 によるクロッシング	d	e	e
6	ピーク 2 によるクロッシング	右端	d	h	d
7	ピーク 6 によるクロッシング	ピーク 8 によるクロッシング	f	g	g
8	ピーク 6 によるクロッシング	右端	f	h	f
9	ピーク 8 によるクロッシング	左の端点によるクロッシング	h	i	i

ヒント

最初に findpeaks を使用して信号のピークを推定し、次に refinepeaks を使用してその振幅と位置を改善することができます。

振幅が y で位置が x である信号があると仮定します。次のコードの抜粋は、y と x からピークを推定して改善する方法を示しています。

[yPeaks,xPeaksIdx] = findpeaks(y);
[yRPeaks,xRPeaks] = refinepeaks(y,xPeaksIdx,x)

拡張機能

すべて展開する

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

findpeaks 関数は、コード生成で datetime の入力をサポートしていません。

GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意および制限:

findpeaks 関数は、コード生成で datetime の入力をサポートしていません。

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2007b で導入

すべて展開する

R2024b: `findpeaks` は GPU コード生成をサポートする

関数 findpeaks は、グラフィックス処理装置 (GPU) 用のコード生成をサポートします。CUDA^® コードを生成するには、MATLAB^® Coder™ および GPU Coder™ が必要です。

参考

findpeaks

構文

説明

例

ベクトルにおけるピークを検出します。

ピークとその位置の検索

ピークのプロミネンス

最小離隔距離のピークの検出

ピーク特性の制約

飽和した信号のピーク

ピーク幅の特定

非線形最小二乗法によるピークの改善

入力引数

y — 入力データ ベクトル

x — 位置 ベクトル | datetime 配列

Fs — サンプル レート 正のスカラー

名前と値の引数

NPeaks — ピークの最大数 正の整数スカラー

SortStr — ピークの並べ替え 'none' (既定値) | 'ascend' | 'descend'

MinPeakHeight — ピーク高の最小値 -Inf (既定値) | 実数スカラー

MinPeakProminence — 最小ピークのプロミネンス 0 (既定値) | 非負の実数スカラー

Threshold — 最小高さ距離 0 (既定値) | 非負の実数スカラー

MinPeakDistance — 最小ピーク離隔距離 0 (既定値) | 正の実数のスカラー

WidthReference — 幅の測定値の基準の高さ 'halfprom' (既定値) | 'halfheight'

MinPeakWidth — 最小ピーク幅 0 (既定値) | 正の実数のスカラー

MaxPeakWidth — 最大ピーク幅 Inf (既定値) | 正の実数のスカラー

Annotate — プロットのスタイル 'peaks' (既定値) | 'extents'

出力引数

pks — 局所的最大値 ベクトル

locs — ピークの位置 ベクトル

w — ピーク幅 ベクトル

p — ピークのプロミネンス ベクトル

詳細

プロミネンス

ヒント

拡張機能

C/C++ コード生成 MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU コード生成 GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

GPU 配列 Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

バージョン履歴

R2024b: findpeaks は GPU コード生成をサポートする

参考

トピック

`y` — 入力データ
ベクトル

`x` — 位置
ベクトル | `datetime` 配列

`Fs` — サンプルレート
正のスカラー

`NPeaks` — ピークの最大数
正の整数スカラー

`SortStr` — ピークの並べ替え
`'none'` (既定値) | `'ascend'` | `'descend'`

`MinPeakHeight` — ピーク高の最小値
`-Inf` (既定値) | 実数スカラー

`MinPeakProminence` — 最小ピークのプロミネンス
0 (既定値) | 非負の実数スカラー

`Threshold` — 最小高さ距離
0 (既定値) | 非負の実数スカラー

`MinPeakDistance` — 最小ピーク離隔距離
0 (既定値) | 正の実数のスカラー

`WidthReference` — 幅の測定値の基準の高さ
`'halfprom'` (既定値) | `'halfheight'`

`MinPeakWidth` — 最小ピーク幅
0 (既定値) | 正の実数のスカラー

`MaxPeakWidth` — 最大ピーク幅
`Inf` (既定値) | 正の実数のスカラー

`Annotate` — プロットのスタイル
`'peaks'` (既定値) | `'extents'`

`pks` — 局所的最大値
ベクトル

`locs` — ピークの位置
ベクトル

`w` — ピーク幅
ベクトル

`p` — ピークのプロミネンス
ベクトル

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

R2024b: `findpeaks` は GPU コード生成をサポートする