ピーク解析

ライブスクリプトを開く

この例では、基本的なピーク解析の実行方法を示します。これは次のような問題の解決に役立ちます。信号のピークはどのように検出するのか。ピーク間の距離はどのように測定するのか。トレンドに影響されている信号のピークの振幅はどのように測定するのか。ノイズを含む信号のピークはどのように検出するのか。局所的最小値はどのように検出するのか。

最大値またはピークの検出

チューリッヒ相対黒点数は、太陽黒点の数と大きさの両方を測定します。関数 findpeaks を使用し、位置とピークの値を検出します。

load sunspot.dat
year = sunspot(:,1); 
relNums = sunspot(:,2);
findpeaks(relNums,year)
xlabel('Year')
ylabel('Sunspot Number')
title('Find All Peaks')

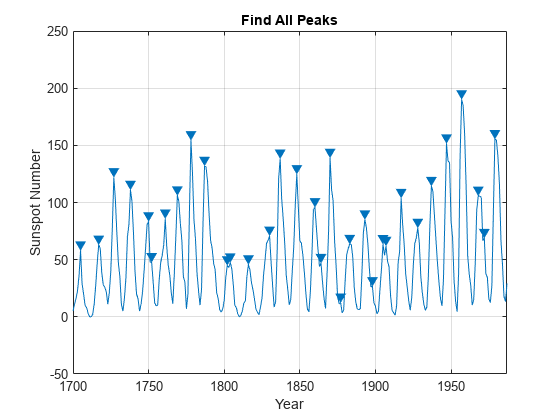
上のプロットは、300 年にわたって表にまとめられた太陽黒点の数を示し、検出されたピークをマークしたものです。次の節では、これらのピーク間の距離を測定する方法を示します。

ピーク間の距離の測定

信号の中のピークは一定の間隔で現れているように見えます。しかし、距離が非常に近いピークがいくつかあります。MinPeakProminence プロパティを使い、これらのピークを除外できます。大きい値を検出する前に、両側で少なくとも相対黒点数が 40 外れているピークを検討します。

findpeaks(relNums,year,'MinPeakProminence',40)
xlabel('Year')
ylabel('Sunspot Number')
title('Find Prominent Peaks')

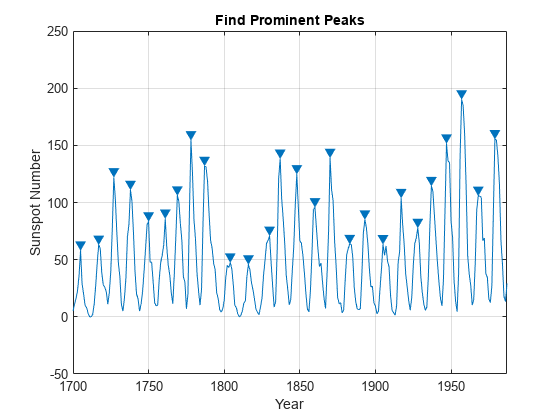
以下のヒストグラムは、ピーク区間の分布を年単位で示しています。

figure
[pks, locs] = findpeaks(relNums,year,'MinPeakProminence',40);
peakInterval = diff(locs);
histogram(peakInterval)
grid on
xlabel('Year Intervals')
ylabel('Frequency of Occurrence')
title('Histogram of Peak Intervals (years)')

AverageDistance_Peaks = mean(diff(locs))

AverageDistance_Peaks = 10.9600

分布は、ピーク区間の大半が 10 ～ 12 年の間にあり、信号に周期性があることを示しています。また、ピーク区間の平均値 10.96 年は既知の太陽の黒点活動周期 11 年と一致します。

切り捨てられた信号または飽和している信号のピーク検出

フラットなピークをピークと考えたり、ピークから除外したりする場合があります。後者の場合、ピークとそのすぐ近傍の振幅の差として定義される最小偏位を threshold プロパティで指定します。

load clippedpeaks.mat

figure

% Show all peaks in the first plot
ax(1) = subplot(2,1,1);
findpeaks(saturatedData)
xlabel('Samples')
ylabel('Amplitude')
title('Detecting Saturated Peaks')

% Specify a minimum excursion in the second plot
ax(2) = subplot(2,1,2);
findpeaks(saturatedData,'threshold',5)
xlabel('Samples')
ylabel('Amplitude')
title('Filtering Out Saturated Peaks')

% link and zoom in to show the changes
linkaxes(ax(1:2),'xy')
axis(ax,[50 70 0 250])

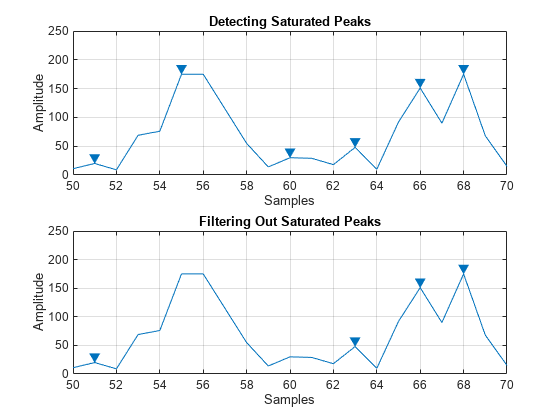
最初のサブプロットは、ピークがフラットな場合に、立ち上がりエッジがピークとして検出されていることを示します。2 番目のサブプロットは、しきい値を指定してフラットなピークを除外することができることを示します。

ピーク振幅の測定

この例では、心電図 (ECG) 信号におけるピーク解析を示します。心電図は経時的な心臓の電気活動の測定値です。信号は皮膚に装着された電極で測定します。このため、電源干渉や動きによるアーチファクトなどのノイズに敏感です。

load noisyecg.mat
t = 1:length(noisyECG_withTrend);

figure
plot(t,noisyECG_withTrend)
title('Signal with a Trend')
xlabel('Samples');
ylabel('Voltage(mV)')
legend('Noisy ECG Signal')
grid on

データのトレンド除去

上記の信号はベースラインシフトであるため、真の振幅を表していません。トレンドを除去するために、信号を低次の多項式で近似し、その多項式を使用してデータのトレンド除去を行います。

[p,s,mu] = polyfit((1:numel(noisyECG_withTrend))',noisyECG_withTrend,6);
f_y = polyval(p,(1:numel(noisyECG_withTrend))',[],mu);

ECG_data = noisyECG_withTrend - f_y;        % Detrend data

figure
plot(t,ECG_data)
grid on
ax = axis;
axis([ax(1:2) -1.2 1.2])
title('Detrended ECG Signal')
xlabel('Samples')
ylabel('Voltage(mV)')
legend('Detrended ECG Signal')

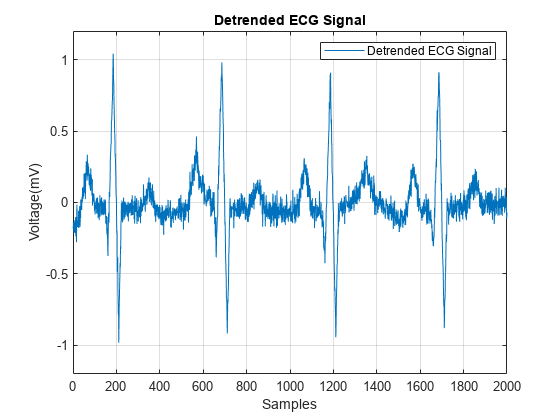
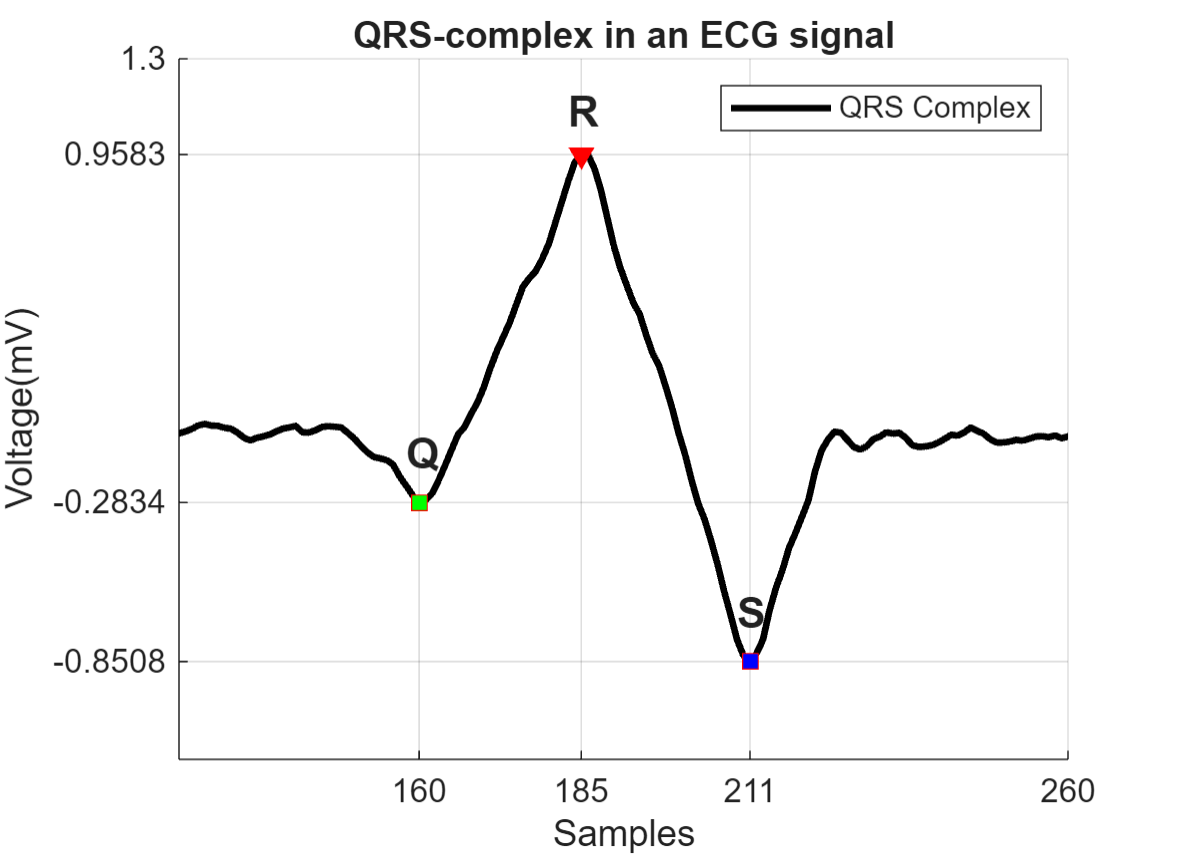
トレンドを除去した後、ECG 信号において繰り返し出現する最も突出したピーク波の QRS 群を検出します。QRS 群は、心臓の左右の心室の脱分極に対応しています。QRS 群は、患者の心拍数の測定や心機能の異常の予見に使用されます。次の図は、ECG 信号の QRS 群の波形を示しています。

対象ピーク検出用しきい値の設定

QRS 群は 3 つの主要な成分から構成されています。Q 波、R 波、S 波です。R 波は、ピークのしきい値を 0.5 mV より上に設定することで検出できます。R 波の間隔が 200 サンプルを超えていることがわかります。この情報を使用して 'MinPeakDistance' を指定して望ましくないピークを除去します。

[~,locs_Rwave] = findpeaks(ECG_data,'MinPeakHeight',0.5,...
                                    'MinPeakDistance',200);

S 波を検出するために、信号の局所的最小値を検出し、しきい値を適切に設定します。

信号の局所的最小値の検出

局所的最小値は、元の信号を反転したバージョンについてピーク検出を行うことで検出できます。

ECG_inverted = -ECG_data;
[~,locs_Swave] = findpeaks(ECG_inverted,'MinPeakHeight',0.5,...
                                        'MinPeakDistance',200);

次のプロットは信号で検出された R 波と S 波です。

figure
hold on 
plot(t,ECG_data)
plot(locs_Rwave,ECG_data(locs_Rwave),'rv','MarkerFaceColor','r')
plot(locs_Swave,ECG_data(locs_Swave),'rs','MarkerFaceColor','b')
axis([0 1850 -1.1 1.1])
grid on
legend('ECG Signal','R waves','S waves')
xlabel('Samples')
ylabel('Voltage(mV)')
title('R wave and S wave in Noisy ECG Signal')

次に、Q 波の位置を判別します。Q 波はノイズに埋もれているため、ピークのしきい値設定により Q 波を見つけようとすると望ましくないピークが検出されます。最初に信号のフィルター処理を行い、それからピークを検出します。信号からノイズを除去するために Savitzky-Golay フィルターを使用します。

smoothECG = sgolayfilt(ECG_data,7,21);

figure
plot(t,ECG_data,'b',t,smoothECG,'r')
grid on
axis tight
xlabel('Samples')
ylabel('Voltage(mV)')
legend('Noisy ECG Signal','Filtered Signal')
title('Filtering Noisy ECG Signal')

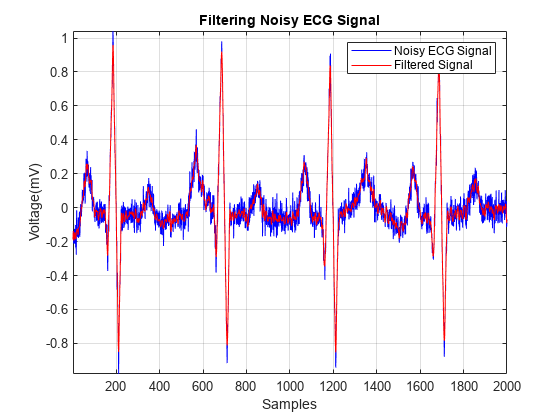
平滑化した信号に対してピーク検出を行い、論理インデックスを使用して Q 波の位置を見つけます。

[~,min_locs] = findpeaks(-smoothECG,'MinPeakDistance',40);

% Peaks between -0.2mV and -0.5mV
locs_Qwave = min_locs(smoothECG(min_locs)>-0.5 & smoothECG(min_locs)<-0.2);

figure
hold on
plot(t,smoothECG); 
plot(locs_Qwave,smoothECG(locs_Qwave),'rs','MarkerFaceColor','g')
plot(locs_Rwave,smoothECG(locs_Rwave),'rv','MarkerFaceColor','r')
plot(locs_Swave,smoothECG(locs_Swave),'rs','MarkerFaceColor','b')
grid on
title('Thresholding Peaks in Signal')
xlabel('Samples')
ylabel('Voltage(mV)')
ax = axis;
axis([0 1850 -1.1 1.1])
legend('Smooth ECG signal','Q wave','R wave','S wave')

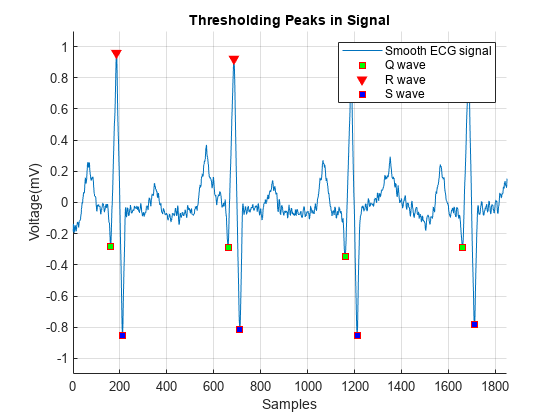
上の図は、ノイズを含む ECG 信号において QRS 群が正しく検出されていることを示しています。

ノイズを含む信号と平滑化された信号との誤差

生の信号の QRS 群とトレンドを除去してフィルター処理された信号の QRS 群とでは平均値が異なっていることに注意してください。

% Values of the Extrema
[val_Qwave, val_Rwave, val_Swave] = deal(smoothECG(locs_Qwave), smoothECG(locs_Rwave), smoothECG(locs_Swave));

meanError_Qwave = mean((noisyECG_withTrend(locs_Qwave) - val_Qwave))

meanError_Qwave = 0.2771

meanError_Rwave = mean((noisyECG_withTrend(locs_Rwave) - val_Rwave))

meanError_Rwave = 0.3476

meanError_Swave = mean((noisyECG_withTrend(locs_Swave) - val_Swave))

meanError_Swave = 0.1844

これは、効率よくピーク解析を行うにはノイズを含む信号のトレンド除去が必要であることを示しています。

ピーク特性

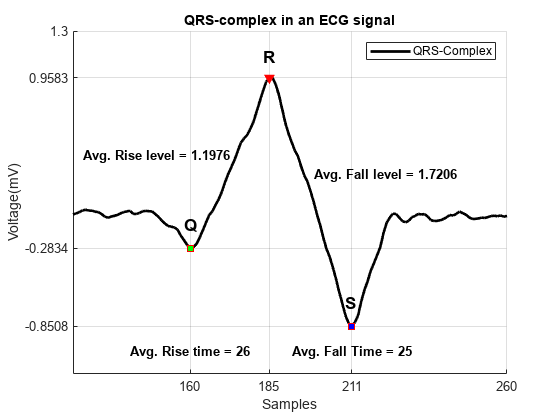
ピークの重要な特性には、立ち上がり時間、立ち下がり時間、立ち上がり振幅、立ち下がり振幅があります。これらの特性は ECG 信号の QRS 群のそれぞれについて計算されます。これらの特性の平均値が下図に表示されます。

avg_riseTime = mean(locs_Rwave-locs_Qwave); % Average Rise time
avg_fallTime = mean(locs_Swave-locs_Rwave); % Average Fall time
avg_riseLevel = mean(val_Rwave-val_Qwave);  % Average Rise Level
avg_fallLevel = mean(val_Rwave-val_Swave);  % Average Fall Level

helperPeakAnalysisPlot(t,smoothECG,...
                    locs_Qwave,locs_Rwave,locs_Swave,...
                    val_Qwave,val_Rwave,val_Swave,...
                    avg_riseTime,avg_fallTime,...
                    avg_riseLevel,avg_fallLevel)

参考

findpeaks