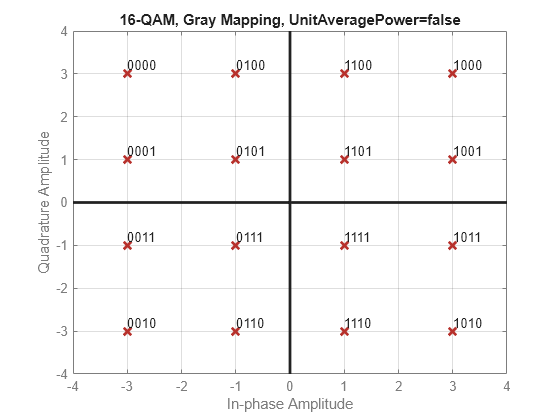
シンボルマッピングの例

グレイ符号の順序とバイナリ符号の順序のエラーレートの比較

PSK 変調を使用して、グレイ符号化とバイナリ符号化を比較します。このシミュレーションは、ビットエネルギーとノイズパワースペクトル密度の比 ( $E_{b} / N_{0}$ ) の値の範囲に対して反復実行され、各 $E_{b} / N_{0}$ 点についてグレイ符号化が指定したビットエラーの最大数 (maxNumErrs) またはビットの最大数 (maxNumBits) に達するまで実行されます。

初期化

システム変数を初期化し、乱数発生器のシードを設定して、結果の再現性を確保します。乱数ストリームシードを設定する前に、乱数発生器の状態を保存し、例の最後に復元します。

M = 8;          % Modulation order for 8-PSK
spf = 10000;    % Samples per frame
maxNumErrs=100; % Stop simulation if 100 errors reached
maxNumBits=1e8; % Stop simulation if 1e8 bits transmitted

prevState = rng(529558);

シンボルエラーレート計算機 System object とビットエラーレート計算機 System object を作成し、復調された整数およびビットデータと元のソースデータを比較します。この比較により、シンボルエラーおよびビットエラーの統計値が生成されます。エラーレート計算機 System object の出力は、計算されたエラーレート、観測された誤り数、および処理されたデータ量から構成された 3 要素ベクトルになります。シミュレーションでは 3 要素ベクトルを使用して、シミュレーションを停止するタイミングを決定します。

symerrorg = comm.ErrorRate;
biterrorg = comm.ErrorRate;
biterrorb = comm.ErrorRate;

フレーム処理ループ

グレイ符号コンスタレーションとバイナリ符号コンスタレーションにマッピングされた 8-PSK 変調を使用して、データの符号化、変調、および復調を行うフレーム処理ループを構成します。このループは、0 ～ 12 dB の範囲の $E_{b} / N_{0}$ 値について 2 dB 刻みで通信システムをシミュレートします。convertSNR関数は、処理ループのために $E_{b} / N_{0}$ 値を SNR に変換します。

各 $E_{b} / N_{0}$ 値について、グレイ符号化されたビットのビットエラーレート計算機 System object で処理されるエラーの最大数 (maxNumErrs) またはビットの最大数 (maxNumBits) のいずれかに達すると、シミュレーションは停止します。

EbNoVec = 0:2:12; % Eb/No values to simulate
snrVec = convertSNR(EbNoVec,"ebno","snr",BitsPerSymbol=log2(M));
SERVec = zeros(size(EbNoVec)); % SER history for Gray ordered
BERVecg = zeros(size(EbNoVec)); % BER history for Gray ordered
BERVecb = zeros(size(EbNoVec)); % BER history for binary ordered
for p = 1:length(EbNoVec)
  % Reset System objects
  reset(symerrorg);
  reset(biterrorg);
  reset(biterrorb);
  % Reset SER and BER for the current Eb/No value
  SER = zeros(3,1);
  BERg = zeros(3,1);
  BERb = zeros(3,1);
  while (BERg(2)<maxNumErrs) && (BERg(3)<maxNumBits)
    % Generate random data
    txSym = randi([0 M-1],spf,1,"uint8");
    txBits = int2bit(txSym,log2(M),true); % Convert symbols to bits
    txg = pskmod(txBits,M,0,"gray",InputType="bit");
    txb = pskmod(txBits,M,0,"bin",InputType="bit");
    rxg = awgn(txg,snrVec(p));
    rxb = awgn(txb,snrVec(p));
    rxBitsg = pskdemod(rxg,M,0,"gray", ...
        OutputType="bit",OutputDataType="uint8");
    rxBitsb = pskdemod(rxb,M,0,"bin", ...
        OutputType="bit",OutputDataType="uint8");
    rxSym = bit2int(rxBitsg,log2(M),true);
    SER = symerrorg(txSym,rxSym); % SER for Gray-coded data 
    BERg = biterrorg(txBits,rxBitsg); % BER for Gray-coded data
    BERb = biterrorb(txBits,rxBitsb); % BER for binary-coded data
  end
  % Save history of SER and BER values
  SERVec(p) = SER(1);
  BERVecg(p) = BERg(1);
  BERVecb(p) = BERb(1);
end

既定のストリームを復元します。

rng(prevState)

結果分析

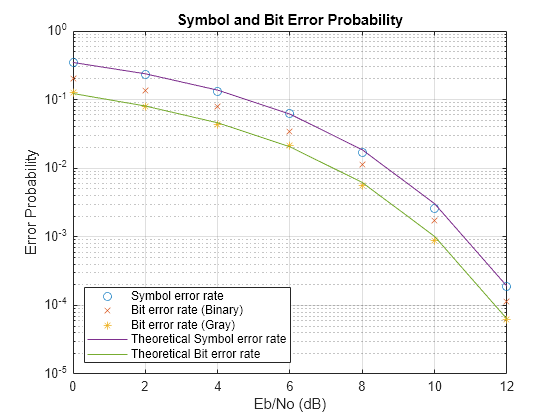
この例のデータを解析して、理論上の性能とシミュレーションでの性能を比較します。関数berawgnを使用して、理論上の誤り確率を計算します。シミュレートされたシンボルエラーレート、グレイ符号化とバイナリ符号化のビットエラーレート、およびグレイ符号化の理論上のシンボルエラー確率とビットエラー確率をプロットします。

[theorBER,theorSER] = berawgn(EbNoVec,"psk",M,"nondiff");

figure;
semilogy( ...
    EbNoVec,SERVec,"o", ...
    EbNoVec,BERVecb,"x", ...
    EbNoVec,BERVecg,"*", ...
    EbNoVec,theorSER,"-", ...
    EbNoVec,theorBER,"-");
legend("Symbol error rate", "Bit error rate (Binary)", ...
    "Bit error rate (Gray)", "Theoretical symbol error rate", ...
    "Theoretical bit error rate", "Location","SouthWest");
xlabel("Eb/No (dB)"); 
ylabel("Error Probability");
title("Symbol and Bit Error Probability");
grid on;

Figure contains an axes object. The axes object with title Symbol and Bit Error Probability, xlabel Eb/No (dB), ylabel Error Probability contains 5 objects of type line. One or more of the lines displays its values using only markers These objects represent Symbol error rate, Bit error rate (Binary), Bit error rate (Gray), Theoretical symbol error rate, Theoretical bit error rate.

Simulink を使用した AWGN チャネルのグレイ符号 M-PSK 変調エラーレート

この例では次を使用します。

モデルを開く

この例では、doc_gray_code を使用して、M-PSK 変調のビットエラーレート (BER) とシンボルエラーレート (SER) を計算します。AWGN 環境下での M-PSK 変調の理論上のエラーレート性能を、グレイ符号シンボルマッピングのエラーレート性能およびバイナリ符号シンボルマッピングのエラーレート性能と比較します。

Random Integer Generator ブロックはソースとして機能し、整数のシーケンスを生成します。Integer to Bit Converter ブロックは、各整数を対応するバイナリ表現に変換します。doc_gray_code モデルのM-PSK Modulator Basebandブロックは、次を行います。

[0, (M - 1] の範囲の整数を表すバイナリ値の入力を受け入れる。ここで、M は変調次数です。
グレイ符号の順序付けを使用して、バイナリ表現をコンスタレーション点に割り当てる。
[0, (2 $\pi$ (M - 1) / M)] の範囲の等間隔の位相をもつ、単位振幅の複素フェーザ出力を生成する。

AWGN Channel ブロックは、変調されたデータにホワイトガウスノイズを付加します。M-PSK Demodulator Baseband ブロックは、ノイズを含むデータを復調します。Bit to Integer Converter ブロックは、各バイナリ表現を、対応する整数に変換します。次に、2 つの個別のError Rate Calculationブロックが、復調されたデータのエラーレートを計算します。"SER Calculation" というラベルの付いたブロックは整数データを比較してシンボルエラーレートの統計を計算し、"BER Calculation" というラベルの付いたブロックはビットデータを比較してビットエラーレートの統計を計算します。Error Rate Calculation ブロックの出力は、計算されたエラーレート、観察された誤り数、および処理されたデータ量を含む 3 要素ベクトルになります。

シミュレーションの実行時間を短縮し、かつ Eb/N0 比が増加してもエラーの統計値が確実に安定するように、モデルは 100 個のエラーが発生するか 1e8 ビットが送信されるまで実行するように構成されています。

モデルは、コールバック関数 PreLoadFcn を使用して、ブロックパラメーターの構成に使用する変数を初期化します。詳細については、モデルコールバック (Simulink)を参照してください。

エラーレート曲線の生成

関数berawgnを使用して、AWGN 環境下での非差分 8-PSK の理論上の BER を Eb/N0 値の範囲にわたって計算します。グレイ符号シンボルマッピングを使用し、同じ範囲の Eb/N0 値にわたって doc_gray_code モデルをシミュレーションします。

"Constellation orders" パラメーターを Gray ではなく Binary に設定するように M-PSK Modulator Baseband ブロックと M-PSK Demodulator Baseband ブロックを変更して、グレイ符号化とバイナリ符号化を比較します。バイナリ符号シンボルマッピングを使用し、同じ範囲の Eb/N0 値にわたって doc_gray_code モデルをシミュレーションします。

関数semilogyを使用して結果をプロットします。グレイ符号システムは、バイナリ符号システムよりも優れたエラーレート性能を実現します。さらに、グレイ符号のエラーレートは、理論上のエラーレート統計と一致しています。

グレイ符号化の変調信号

ライブスクリプトを開く

PSK、DPSK、FSK、QAM、および PAM の変調タイプの場合、グレイコンスタレーションは、対応する変調関数の System object™ またはブロックでシンボルマッピングをグレイ符号化に設定することによって取得されます。既定のシンボル順序は、グレイ符号化された順序を変調のために使用します。

変調関数の場合、"gray"、"bin"、またはカスタムのシンボル順序を指定するベクトルを指定できます。この例では、グレイ符号化されたシンボルマッピングで関数qammodを使用します。コンスタレーションプロットをチェックすると、隣接要素がすべて 1 ビットずつ異なっているため、変調されたシンボルがグレイ符号化されていることがわかります。

k = 4;
M = 2^k;
y = int2bit([0:M-1]',k,false);
symorder = "gray";
xmap = qammod(y,M,symorder, ...
    InputType="bit", ...
    PlotConstellation=true);

Figure contains an axes object. The axes object with title 16-QAM, Gray Mapping, UnitAveragePower=false, xlabel In-phase Amplitude, ylabel Quadrature Amplitude contains 19 objects of type line, text. One or more of the lines displays its values using only markers