probplot
確率プロット
構文
説明
probplot( は、y)y 内のデータの分布を正規分布と比較する正規確率プロットを作成します。
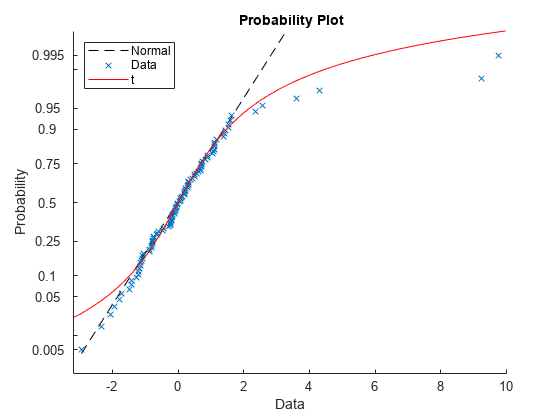
probplot は、マーカー記号を使用して y 内の各データ点をプロットし、理論的な分布を表す基準線を描画します。標本データが正規分布に従っている場合、データ点は基準線に沿って現れます。基準線は、データの 1 番目と 3 番目の四分位数を結んで、データの端まで伸びます。正規分布ではない場合、データ プロットが曲がります。
probplot( は、前の構文のいずれかの入力引数を使用して、ax,___)ax で指定された既存の確率プロットの座標軸に確率プロットを追加します。
probplot(___,'noref') は、プロットの基準線を省略します。
例
標本データを生成し、確率プロットを作成します。
標本データを生成します。標本 x1 には、スケール パラメーターが A = 3 で、形状パラメーターが B = 3 のワイブル分布からの 500 個の乱数が含まれています。標本 x2 には、スケール パラメーターが B = 3 のレイリー分布からの 500 個の乱数が含まれています。
rng('default'); % For reproducibility x1 = wblrnd(3,3,[500,1]); x2 = raylrnd(3,[500,1]);
x1 および x2 のデータが、ワイブル分布から派生しているかどうかを評価する確率プロットを作成します。
figure probplot('weibull',[x1 x2]) legend('Weibull Sample','Rayleigh Sample','Location','best')
確率プロットには、x1 データがワイブル分布から派生しており、x2 データはワイブル分布から派生していないことが示されます。
または、wblplot を使用してワイブル確率プロットを作成できます。
確率プロットと追加の近似直線を同じ Figure に作成します。
裾に約 20% の外れ値が含まれる標本データを生成します。標本データの左側の裾には、パラメーターが mu = 1 である指数分布から無作為に生成された 10 個の値が含まれます。右側の裾には、パラメーターが mu = 5 の指数分布からランダムに生成された 10 個の値が含まれます。標本データの中心には、標準の正規分布から無作為に生成された 80 個の値が含まれます。
rng('default') % For reproducibility left_tail = -exprnd(1,10,1); right_tail = exprnd(5,10,1); center = randn(80,1); data = [left_tail;center;right_tail];
標本データが正規分布から派生しているかどうかを評価するため、確率プロットを作成します。
probplot(data)
同じ Figure に t 位置-スケール曲線をプロットし、data と比較します。
p = mle(data,'distribution','tLocationScale'); t = @(data,mu,sig,df)cdf('tLocationScale',data,mu,sig,df); h = probplot(gca,t,p); h.Color = 'r'; h.LineStyle = '-'; title('{\bf Probability Plot}') legend('Normal','Data','t','Location','NW')
このプロットは、外れ値のため正規分布の直線も t 位置-スケール曲線も裾を十分には近似していないことを示しています。
半正規分布確率プロットを作成して、化学製品製造工程で流量に影響を与える可能性がある因子を調べる実験における有意な効果を特定します。4 つの因子は、反応物 A、B、C および D です。各因子は、2 つのレベル (高濃度と低濃度) で存在します。この実験では、各因子レベルにおける反復は 1 つだけです。
標本データを読み込みます。
load flowrateテーブル flowrate の最初の 4 列には、因子およびその交互作用の計画行列が格納されています。計画行列は、高因子レベルには 1、低因子レベルには -1 を使用して符号化されています。flowrate の 5 列目には、測定された流量が格納されています。
rate を応答変数として使用して、線形回帰モデルを当てはめます。予測子変数 A、B、C、D およびこれらの交互作用項をすべて使用します。
mdl = fitlm(flowrate,'rate ~ A*B*C*D');因子効果の推定値の絶対値を計算して格納します。因子効果の推定値を取得するため、モデル近似時に取得した係数推定値に 2 を乗算します。回帰係数は x の 1 単位の変化が y の平均に与える影響を測るため、このステップが必要です。ただし、計画行列では -1 と 1 で符号化しているので、効果の推定値は x の 2 単位の変化を測ります。ベースライン尺度は除外します。mdl 内の因子の順序は元の計画行列内の順序と異なる可能性があることに注意してください。
effects = abs(mdl.Coefficients{2:end,1}*2);ベースラインを除く効果の推定値の絶対値を使用して、半正規確率プロットを作成します。
figure
h = probplot('halfnormal',effects);
点にラベルを付け、プロットの書式を設定します。まず、昇順で並べ替えられた効果の推定値のインデックス値を返します。次に、これらのインデックス値を使用して、グラフィックス ハンドルに格納されている確率値 (h(1).YData) を並べ替えます。
[b,i] = sort(effects); prob(i) = h(1).YData;
各点でテキスト ラベルをプロットに追加します。各点で、x 値は効果の推定値、y 値は対応する確率です。
text(effects,prob,mdl.CoefficientNames(2:end),'FontSize',8,... 'VerticalAlignment','top') h(1).Color = 'r';
基準線から離れた位置にある点は、有意な効果を表します。
シミュレーションによる度数データを生成します。
y = 1:10; freq = [2 4 6 7 9 8 7 7 6 5];
度数データを使用して正規確率プロットを作成します。
probplot(y,[],freq)
この正規確率プロットは、データが正規分布になっていないことを示しています。
入力引数
出力引数
アルゴリズム
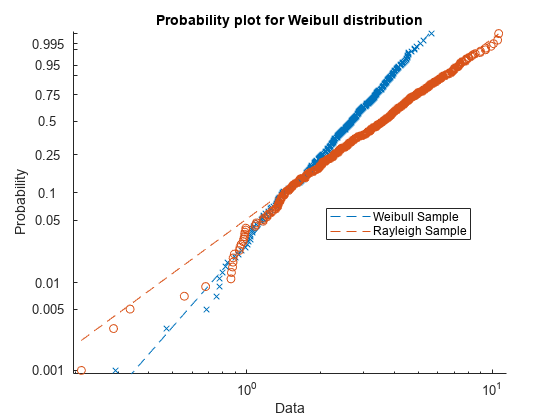
probplot は、与えられた確率分布の分位数に標本データの分位数を一致させます。標本データは並べ替えられ、dist の選択に従ってスケーリングされ、x 軸に対してプロットされます。dist が 'lognormal'、'loglogistic' または 'weibull' である場合、スケーリングは対数になります。それ以外では、スケーリングは線形です。y 軸は、dist で指定された分布の分位数を、確率値に変換して表します。スケーリングは与えられた分布によって異なり、線形ではありません。
サイズが N の標本を並べ替えた i 番目の値が x 軸の値である場合、y 軸の値はデータの経験累積分布関数に対する評価点間の中点です。データが打ち切られていない場合、中点は に等しくなります。
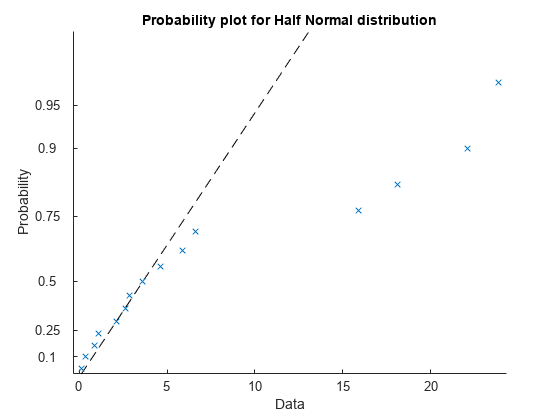
probplot は、プロットの線形性を評価するため、基準線を重ね合わせます。データが打ち切られていない場合、この線はデータの 1 番目と 3 番目の四分位数を通過します。データが打ち切られている場合、それに従って線が移動します。データが打ち切られておらず、dist が 'half normal' である場合、probplot は 0 番目と 2 番目の四分位数を代わりに使用します。
バージョン履歴
R2006a より前に導入
