このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

分布プロット

"分布プロット" では、指定された分布から予想される理論値とデータの経験的分布を比較することにより、標本データの分布を視覚的に評価します。より正式な仮説検定に加えて分布プロットを使用して、標本データが特定の分布から派生しているかどうかを調べます。仮説検定の詳細については、仮説検定を参照してください。

Statistics and Machine Learning Toolbox™ には、分布プロットのオプションがいくつか用意されています。

• 正規確率プロット — normplot を使用して、標本データが正規分布から派生しているかどうかを評価します。probplot を使用して、正規分布以外の分布について確率プロットを作成したり、打ち切られたデータの分布を調べます。plot を使用して、確率分布オブジェクトの確率プロットをプロットします。

• 分位数-分位数 (QQ) プロット — qqplot を使用して、2 組の標本データが同じ分布族から派生しているかどうかを評価します。このプロットは、位置およびスケールの違いに対してロバストです。

• 累積分布プロット — cdfplot または ecdf を使用して、指定した分布の理論的な経験的累積分布関数 (cdf) と視覚的に比較するため、標本データの cdf を表示します。plot を使用して、確率分布オブジェクトの累積分布関数をプロットします。

正規確率プロット

データが正規分布から派生しているかどうかを評価するには、正規確率プロットを使用します。多くの統計学的手法では、基となる分布が正規分布であると仮定します。正規確率プロットは、この仮定の正当性に対する何らかの保証を提供するか、仮定に問題があるという警告を与えることができます。正規性の解析では、通常、正規確率プロットと正規性の仮説検定を組み合わせます。

この例では、平均が 10、標準偏差が 1 の正規分布から 25 個の乱数のデータ標本を生成し、データの正規確率プロットを作成します。

rng('default');  % For reproducibility
x = normrnd(10,1,[25,1]);
normplot(x)

プラス記号は、それぞれのデータ点の値に対する経験的確率をプロットしています。実線はデータの 25 番目と 75 番目の百分位数を繋いだ線を表し、この線をデータの両端まで破線により延長します。 y 軸の値は、0 から 1 までの確率で、スケールは線形ではありません。 y 軸上の目盛間の距離は、正規分布の分位数間の距離を示しています。分位数は、中央値 (50 番目の百分位数) の近くでは密集し、中央値から離れるにつれて対称的に広がります。

正規確率プロットでは、すべてのデータ点が線の近くにある場合、正規分布に従っているという仮定が正しいことを示します。それ以外の場合、正規性の仮定は正当化されません。たとえば、以下は平均が 10 の指数分布から 100 個の乱数のデータ標本を生成し、データの正規確率プロットを作成します。

x = exprnd(10,100,1);
normplot(x)

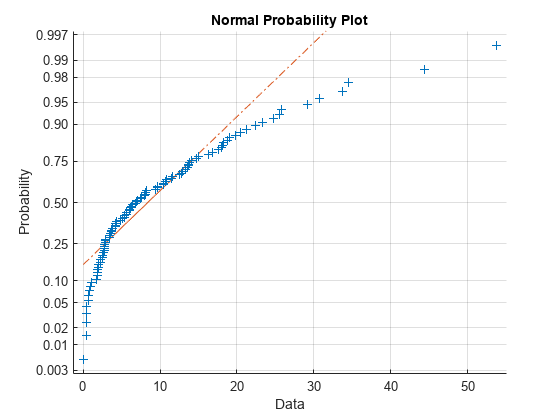
この図は、データが基本的な正規分布でないことを明確に示しています。

確率プロット

正規確率プロットのように、確率プロットは、ちょうど、特定の分布にスケーリングされる経験的な累積密度関数プロットです。 y 軸の値は、0 から 1 までの確率で、スケールは線形ではありません。目盛間の距離は、この分布の分位数間の距離を示しています。プロットでは、データの 1 番目と 3 番目の quartiles の間に線が描かれています。データが線の近くにある場合、分布をデータに対するモデルとして選択することは妥当です。通常、分布の解析では、特定の分布に対して確率プロットと仮説検定を組み合わせます。

ワイブル確率プロットの作成

標本データを生成し、確率プロットを作成します。

標本データを生成します。標本 x1 には、スケール パラメーターが A = 3 で、形状パラメーターが B = 3 のワイブル分布からの 500 個の乱数が含まれています。標本 x2 には、スケール パラメーターが B = 3 のレイリー分布からの 500 個の乱数が含まれています。

rng('default');  % For reproducibility
x1 = wblrnd(3,3,[500,1]);
x2 = raylrnd(3,[500,1]);

x1 および x2 のデータが、ワイブル分布から派生しているかどうかを評価する確率プロットを作成します。

figure
probplot('weibull',[x1 x2])
legend('Weibull Sample','Rayleigh Sample','Location','best')

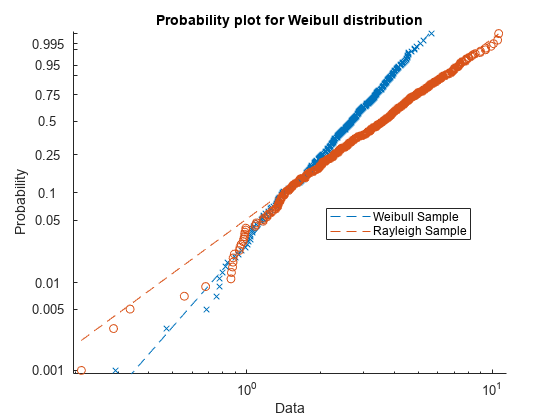
確率プロットには、x1 データがワイブル分布から派生しており、x2 データはワイブル分布から派生していないことが示されます。

または、wblplot を使用してワイブル確率プロットを作成できます。

ガンマ確率プロットの作成

形状パラメーターが 9、スケール パラメーターが 2 のガンマ分布から乱数データを生成します。

rng("default") %set the random seed for reproducibility
gammadata = gamrnd(9,2,100,1);

ガンマ分布とロジスティック分布をデータに当てはめ、結果を GammaDistribution オブジェクトと LogisticDistribution オブジェクトに格納します。

gammapd = fitdist(gammadata,"Gamma");
logisticpd = fitdist(gammadata,"Logistic");

データに当てはめた分布を確率プロットで比較します。

tiledlayout(1,2)
nexttile
plot(logisticpd,'PlotType',"probability")
title("Logistic Distribution")
nexttile
plot(gammapd,'PlotType',"probability")
title("Gamma Distribution")

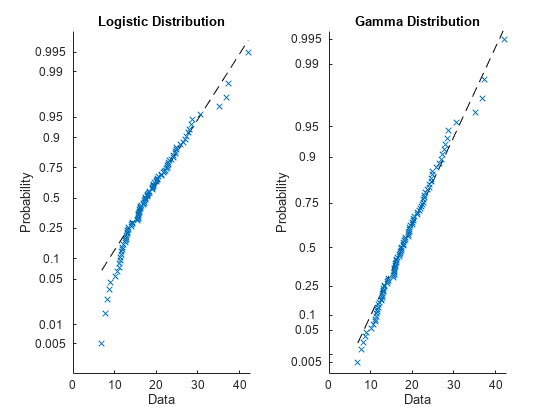
確率プロットから、ガンマ分布の方がデータへの適合が高いことがわかります。

分位数-分位数 (QQ) プロット

2 つの標本が同じ分布族から派生しているかどうかを判定するには、分位数-分位数 (q-q) プロットを使用します。q-q プロットは、各標本から計算される分位数の散布図であり、1 番目と 3 番目の分位数の間に線が描かれます。データが線の近くにある場合、2 つの標本が同じ分布によるものであると仮定することは妥当です。この方法は、どちらの分布の位置とスケールの変化に対してもロバストです。

分位数-分位数プロットを作成するには、関数 qqplot を使用します。

次の例では、パラメーター値の異なるポアソン分布から乱数を含むデータ標本を 2 つ生成し、分位数-分位数プロットを作成します。x のデータは平均が 10 のポアソン分布から、y のデータは平均が 5 のポアソン分布から派生しています。

x = poissrnd(10,[50,1]);
y = poissrnd(5,[100,1]);
qqplot(x,y)

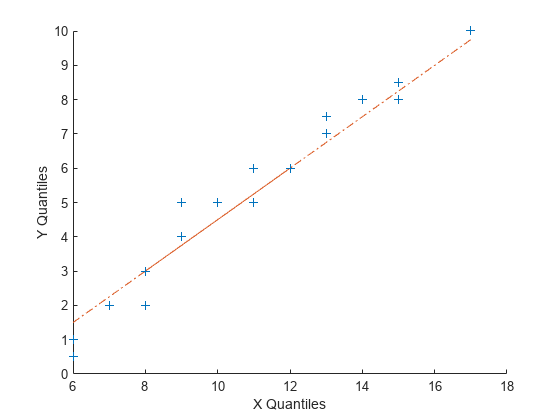
パラメーターや標本のサイズは異なっていますが、直線関係で近似できることは、2 つの標本が同じ分布族からの標本である可能性を示します。正規確率プロットと同様に、仮説検定からもそのような仮説の正当性をより確実にすることができます。ただし、同じ分布からの 2 つの標本に依存する統計手法として、線形の分位数-分位数プロットが十分であることがしばしばあります。

次の例は、異なる分布による標本ではどのようになるかを示しています。ここで、x には平均が 5、標準偏差が 1 の正規分布から生成した 100 個の乱数が、y にはスケール パラメーターが 2、形状パラメーターが 0.5 のワイブル分布から生成した 100 個の乱数が含まれています。

x = normrnd(5,1,[100,1]);
y = wblrnd(2,0.5,[100,1]);
qqplot(x,y)

このプロットは、明らかにこれらの標本が同じ分布族からは派生していないことを示しています。

累積分布プロット

経験的累積分布関数 (cdf) プロットは、x の各値以下であるデータの比率を x の関数として示します。y 軸のスケールは線形で、特定の分布に対してはスケーリングされません。データの経験的累積分布関数プロットは、特定の分布の累積分布関数と比較するために使われます。

経験的累積分布関数プロットを作成するには、関数 cdfplot または関数 ecdf を使用します。

経験的 cdf と理論的な cdf の比較

標本データセットの経験的 cdf をプロットし、標本データセットの基となる分布の理論的な cdf と比較します。実際には、理論的な cdf は不明な場合があります。

位置パラメーターが 0、スケール パラメーターが 3 の極値分布から、ランダムな標本データセットを生成します。

rng('default')  % For reproducibility
y = evrnd(0,3,100,1);

標本データセットの経験的 cdf と理論的な cdf を同じ図にプロットします。

cdfplot(y)
hold on
x = linspace(min(y),max(y));
plot(x,evcdf(x,0,3))
legend('Empirical CDF','Theoretical CDF','Location','best')
hold off

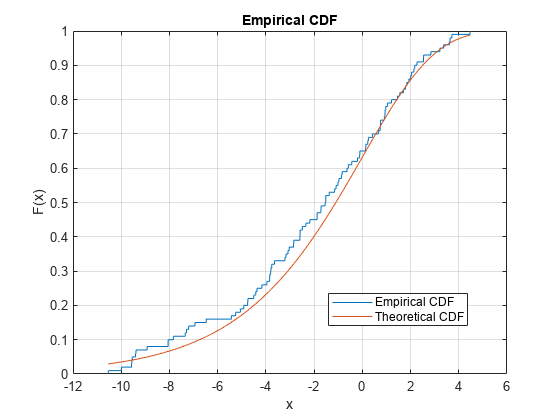
このプロットは、経験的 cdf と理論的な cdf の間の類似性を示します。

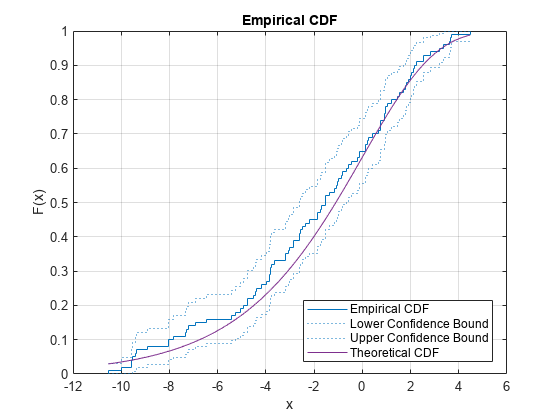
代わりに、関数 ecdf を使用することもできます。関数 ecdf は、グリーンウッドの公式を使用して推定した 95% 信頼区間もプロットします。詳細については、アルゴリズムを参照してください。

ecdf(y,'Bounds','on')
hold on
plot(x,evcdf(x,0,3))
grid on
title('Empirical CDF')
legend('Empirical CDF','Lower Confidence Bound','Upper Confidence Bound','Theoretical CDF','Location','best')
hold off

二項分布の累積分布関数のプロット

試行回数が 10、各試行の成功確率が 0.5 の二項分布を作成します。

binomialpd = makedist("Binomial",10,0.5)

binomialpd = 
  BinomialDistribution

  Binomial distribution
    N =  10
    p = 0.5

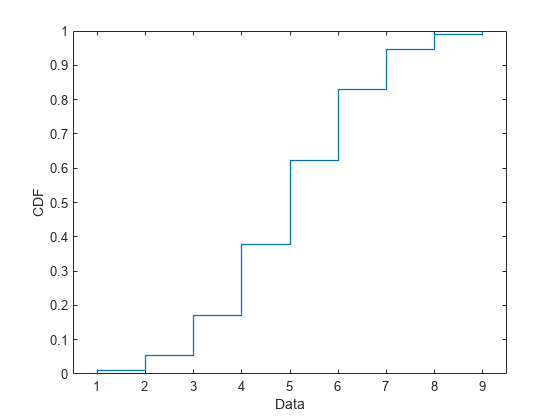
二項分布の累積分布関数をプロットします。

plot(binomialpd,'PlotType',"cdf")

参考

normplot | qqplot | cdfplot | ecdf | probplot | wblplot

関連するトピック

• 箱ひげ図の使用によるグループ化されたデータの比較
• 仮説検定

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい