MultinomialRegression

多項回帰モデル

R2023a 以降

説明

MultinomialRegression は、当てはめ済みの多項回帰モデルオブジェクトです。多項回帰モデルは、予測子と値の有限の集合をもつ応答との間の関係を記述します。

当てはめた多項回帰モデルを調べるには、MultinomialRegression オブジェクトのプロパティを使用します。オブジェクトプロパティには、係数推定値、要約統計量、およびモデルの当てはめに使用されるデータに関する情報が含まれています。オブジェクト関数を使用して、応答の予測や多項回帰モデルの評価と可視化を行います。

作成

MultinomialRegression モデルオブジェクトは、fitmnr を使用してパラメーターの値を指定して作成します。

プロパティ

すべて展開する

係数推定値

`ClassNames` — 応答変数カテゴリの名前
categorical 配列 | 文字配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

このプロパティは読み取り専用です。

多項回帰モデルの当てはめに使用される応答変数カテゴリの名前。k 行 1 列の categorical 配列、文字配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列として指定します。k は応答カテゴリの数です。ClassNames のデータ型は応答カテゴリラベルと同じです。string 配列は文字ベクトルの cell 配列として扱われることに注意してください。ClassNames プロパティは、モデルオブジェクトを作成するときに fitmnr の入力引数 Y または Tbl で設定されます。

`CoefficientCovariance` — モデルの係数の共分散行列
(p+1) 行 (p+1) 列の数値の行列

このプロパティは読み取り専用です。

モデルの係数の共分散行列。(p+1) 行 (p+1) 列の数値の行列として指定します。p は予測子変数の数です。

詳細については、係数の標準誤差と信頼区間を参照してください。

データ型: single | double

`CoefficientNames` — 係数の名前
文字ベクトルの cell 配列

このプロパティは読み取り専用です。

係数の名前。対応する係数の名前をそれぞれ含む文字ベクトルの cell 配列として指定します。各係数の名前は、予測子または切片の名前に応答カテゴリの名前を付加した名前になります。このプロパティは、モデルオブジェクトを作成するときに fitmnr の入力引数 Tbl または名前と値の引数 PredictorNames で設定されます。

データ型: cell

`Coefficients` — 係数の値
テーブル

このプロパティは読み取り専用です。

係数の値。係数ごとに 1 つの行と次の列で構成される table として指定します。

Value — 推定される係数値
SE — 推定の標準誤差
tStat — 係数がゼロであるという帰無仮説をもつ両側検定の t 統計量
pValue — t 統計量の p 値

係数に対する他の検定を実行するには、coefTest または testDeviance を使用します。係数推定値の信頼区間を求めるには、coefCI を使用します。

データ型: table

`IncludeClassInteractions` — 応答カテゴリと係数の間の交互作用を表すインジケーター
`true` または `1` | `false` または `0`

このプロパティは読み取り専用です。

応答カテゴリと係数の間の交互作用を表すインジケーター。数値または logical の 1 (true) または 0 (false) として指定します。このプロパティは、モデルオブジェクトを作成するときに fitmnr の名前と値の引数 IncludeClassInteractions で設定されます。

データ型: logical

`Link` — リンク関数
`'logit'` | `'probit'` | `'comploglog'` | `'loglog'`

このプロパティは読み取り専用です。

順序モデルと階層モデルに使用するリンク関数。'logit'、'probit'、'comploglog'、または 'loglog' として指定します。ノミナルモデルについては、Link は常に 'logit' になります。このプロパティは、モデルオブジェクトを作成するときに fitmnr の名前と値の引数 Link で設定されます。

データ型: char

`ModelType` — モデルのタイプ
`'nominal'` | `'ordinal'` | `'hierarchical'`

このプロパティは読み取り専用です。

モデルのタイプ。'nominal'、'ordinal'、または 'hierarchical' として指定します。このプロパティは、モデルオブジェクトを作成するときに fitmnr の名前と値の引数 ModelType で設定されます。

データ型: char

`NumCoefficients` — モデルの係数の数
正の整数

このプロパティは読み取り専用です。

モデルの係数の数。正の整数として指定します。

データ型: double

要約統計量

`Deviance` — 当てはめの逸脱度
数値

このプロパティは読み取り専用です。

当てはめの逸脱度。数値を指定します。逸脱度は、一方のモデルが他方のモデルの特別なケースである 2 つのモデルを比較するために役立ちます。2 つのモデルの逸脱度の差異は、2 つのモデル間に推定されるパラメーター数の差異と等しい自由度をもつカイ二乗分布になります。詳細については、逸脱度を参照してください。

データ型: single | double

`DFE` — 誤差に対する自由度
正の整数

このプロパティは読み取り専用です。

誤差 (残差) の自由度。正の整数として指定します。ノミナルモデルと順序モデルについては、DFE は次により与えられます。

$D F E = n * (k - 1) - N,$

ここで、n は観測値の数、k は応答カテゴリの数、N はモデルの係数の数です。階層モデルについては、DFE は次により与えられます。

$D F E = n - N,$

これは、IncludeClassInteractions が false の場合です。IncludeClassInteractions が true の場合は、階層モデルの DFE は次により与えられます。

$D F E = (\sum_{i = 1}^{k - 1} n_{i}) - N,$

ここで、n_i は i 番目以上の応答カテゴリに対応する観測値の数です。

データ型: double

`Dispersion` — 分散
数値スカラー

このプロパティは読み取り専用です。

分散。数値スカラーとして指定します。モデルオブジェクトの作成時に fitmnr の名前と値の引数 EstimateDispersion を true に設定すると、関数は Dispersion の値として標準誤差を推定します。それ以外の場合、fitmnr は既定の理論値である 1 を Dispersion に代入します。

データ型: single | double

`EstimateDispersion` — 分散を推定するかどうかを示すインジケーター
`false` | `true`

このプロパティは読み取り専用です。

分散を推定するかどうかを示すインジケーター。logical の false または true として指定します。このプロパティは、モデルオブジェクトを作成するときに fitmnr の名前と値の引数 EstimateDispersion で設定されます。

データ型: single | double | logical

`Fitted` — 入力データを基に当てはめを行った応答値
categorical 配列 | 文字配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

このプロパティは読み取り専用です。

入力データに基づいて当てはめられた (予測された) 応答値。n 行 1 列の categorical 配列、文字配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列として指定します。n は入力データ内の観測値の数です。Fitted のデータ型は応答カテゴリラベルと同じです。string 配列は文字ベクトルの cell 配列として扱われることに注意してください。他の予測子の値についての予測を計算したり、Fitted の信頼限界を計算したりするには、predict を使用します。

`LogLikelihood` — 当てはめたモデルの対数尤度
数値

このプロパティは読み取り専用です。

当てはめたモデルの対数尤度。数値として指定します。各応答値が多項分布に従うという仮定に基づきます。モデルの対数尤度は、fitmnr でモデルオブジェクトを作成する際に応答データの対数確率の和を求めることで計算されます。

データ型: single | double

`ModelCriterion` — モデルの比較基準
構造体

このプロパティは読み取り専用です。

モデルの比較基準。次のフィールドがある構造体を指定します。

AIC — 赤池情報量基準。AIC = –2*lnL + 2*m であり、ここで lnL は対数尤度、m は推定パラメーターの数です。
AICc — 標本サイズについて修正された赤池情報量基準。AICc = AIC + (2*m*(m + 1))/(n – m – 1) であり、ここで n は観測値の数です。
BIC — ベイズ情報量基準。BIC = –2*lnL + m*ln(n) です。
CAIC — 一貫した赤池情報量基準。CAIC = –2*lnL + m*(ln(n) + 1) です。

情報量基準は、同じデータに当てはめた複数のモデルを比較するために使用できるモデル選択ツールです。これらの基準は、尤度に基づくモデル近似の尺度であり、複雑度 (特にパラメーター数) に対するペナルティが含まれています。情報量基準が異なるとペナルティの形式が異なります。

複数のモデルを比較した場合に、情報量基準の値が最も小さいモデルが最良近似モデルです。最良近似モデルは、モデルの比較に使用する基準によって変化する可能性があります。

データ型: struct

`Residuals` — 当てはめたモデルの残差
テーブル

このプロパティは読み取り専用です。

当てはめたモデルの残差。観測値ごとに 1 つの行と応答クラスごとに 1 つの列が各変数に格納された table として指定します。

列説明

列	説明
`Raw`	生の残差。観測値から当てはめ値を減算した値です。 $r_{i j} = y_{i j} - {\hat{π}}_{i j} * m_{i}, {\begin{matrix} i = 1, \dots, n \\ j = 1, \dots, N \end{matrix} .$ y_ij は i 番目のデータ点が j 番目の応答カテゴリに含まれるかどうかを示す logical スカラー ${\hat{π}}_{i j}$ は i 番目のデータ点が j 番目の応答カテゴリに含まれる予測確率 m_i は観測値 i の対応する標本サイズ n と N はそれぞれデータ点と応答カテゴリの数
`Pearson`	生の残差を平方根平均二乗誤差 (RMSE) で除算した値
`Deviance`	次の式で与えられる逸脱度残差 $r d_{i} = 2 * \sum_{j}^{k} y_{i j} * \log (\frac{y_{i j}}{{\hat{π}}_{i j} * m_{i}}), i = 1, \dots, n .$

Raw

生の残差。観測値から当てはめ値を減算した値です。

$r_{i j} = y_{i j} - {\hat{π}}_{i j} * m_{i}, {\begin{matrix} i = 1, \dots, n \\ j = 1, \dots, N \end{matrix} .$

y_ij は i 番目のデータ点が j 番目の応答カテゴリに含まれるかどうかを示す logical スカラー
${\hat{π}}_{i j}$ は i 番目のデータ点が j 番目の応答カテゴリに含まれる予測確率
m_i は観測値 i の対応する標本サイズ
n と N はそれぞれデータ点と応答カテゴリの数

Pearson 生の残差を平方根平均二乗誤差 (RMSE) で除算した値

Deviance

次の式で与えられる逸脱度残差

$r d_{i} = 2 * \sum_{j}^{k} y_{i j} * \log (\frac{y_{i j}}{{\hat{π}}_{i j} * m_{i}}), i = 1, \dots, n .$

欠損値が原因で当てはめに使用されなかった行には NaN 値が格納されます。欠損値を検査するには、ObservationInfo を参照してください。

残差のプロットを作成するには、plotResiduals を使用します。詳細については、残差を参照してください。

データ型: table

`Rsquared` — 当てはめたモデルの疑似決定係数の値
構造体

このプロパティは読み取り専用です。

当てはめたモデルの疑似決定係数の値。構造体として指定します。Rsquared の各フィールドに、それぞれ異なる式で計算された疑似決定係数の値が格納されます[1]。

フィールド説明

フィールド	説明
`'Ordinary'`	通常の疑似決定係数の値 $R^{2} = 1 - \frac{\ln (L_{F u l l})}{\ln (L_{N u l l})},$ ここで、 $L_{F u l l}$ は当てはめたモデルの対数尤度、 $L_{N u l l}$ は予測子をもたないモデルの対数尤度です。
`'Adjusted'`	調整された疑似決定係数の値 $R^{2} = 1 - \frac{\ln (L_{F u l l}) - K}{\ln (L_{N u l l})},$ ここで、K は $L_{F u l l}$ に含まれるモデルの係数の数です。

'Ordinary'

通常の疑似決定係数の値

$R^{2} = 1 - \frac{\ln (L_{F u l l})}{\ln (L_{N u l l})},$

ここで、 $L_{F u l l}$ は当てはめたモデルの対数尤度、 $L_{N u l l}$ は予測子をもたないモデルの対数尤度です。

'Adjusted'

調整された疑似決定係数の値

$R^{2} = 1 - \frac{\ln (L_{F u l l}) - K}{\ln (L_{N u l l})},$

ここで、K は $L_{F u l l}$ に含まれるモデルの係数の数です。

データ型: struct

入力データ

`Formula` — 回帰モデル
`LinearFormula` オブジェクト

このプロパティは読み取り専用です。

回帰モデル。LinearFormula オブジェクトとして指定します。このプロパティは、モデルオブジェクトを作成するときに fitmnr の入力引数 Formula で設定されます。

`NumObservations` — 観測値の数
正の整数

このプロパティは読み取り専用です。

当てはめアルゴリズムでモデルの当てはめに使用される観測値の数。正の整数として指定します。NumObservations は、元の table または行列で提供された観測値から欠損値を含む行を除いた数です。

データ型: double

`NumPredictors` — 予測子変数の数
正の整数

このプロパティは読み取り専用です。

当てはめアルゴリズムでモデルの当てはめに使用される予測子変数の数。正の整数として指定します。

データ型: double

`NumVariables` — 変数の数
正の整数

このプロパティは読み取り専用です。

入力データ内の変数の数。正の整数として指定します。NumVariables には、モデルの当てはめに予測子または応答として使用されない変数もすべて含まれます。

データ型: double

`ObservationInfo` — 観測値の情報
n 行 3 列の table

このプロパティは読み取り専用です。

観測値の情報。次の列を含む n 行 3 列の table として指定されます。ここで、n は観測値の数です。

列	説明
`Weights`	観測値の重み。数値として指定します。既定値は `1` です。
`Missing`	欠損観測値のインジケーター。logical 値として指定します。観測値が欠損値である場合、値は `true` です。
`Subset`	観測値が `fitmnr` で使用されるかどうかを示すインジケーター。logical 値として指定します。観測値が欠損値でなく、つまり観測値が `fitmnr` で使用される場合、値は `true` です。

データ型: table

`ObservationNames` — 観測値の名前
文字ベクトルの cell 配列

このプロパティは読み取り専用です。

観測値の名前。当てはめで使用した観測値の名前が含まれている文字ベクトルの cell 配列を指定します。

当てはめが観測値の名前を含む table またはデータセットに基づいている場合、それらの名前が ObservationNames プロパティに格納されます。
それ以外の場合、ObservationNames は空の cell 配列になります。

このプロパティは、モデルオブジェクトを作成して Tbl に行名を代入するときに fitmnr の入力引数 Tbl で設定されます。

データ型: cell

`PredictorNames` — モデルの当てはめに使用した予測子の名前
文字ベクトルの cell 配列

このプロパティは読み取り専用です。

モデルの当てはめに使用された予測子の名前。文字ベクトルの cell 配列として指定されます。このプロパティは、モデルオブジェクトを作成するときに fitmnr の次のいずれかの引数で設定されます。

入力引数 Tbl
入力引数 X および名前と値の引数 PredictorNames の組み合わせ

データ型: cell

`ResponseName` — 応答変数名
文字ベクトル

このプロパティは読み取り専用です。

応答変数名。文字ベクトルを指定します。このプロパティは、モデルオブジェクトを作成するときに fitmnr の次のいずれかの引数で設定されます。

名前と値の引数 ResponseName
入力引数 Tbl と入力引数 ResponseVarName の組み合わせ
入力引数 Tbl と入力引数 Formula の組み合わせ

データ型: char

`VariableInfo` — 変数に関する情報
テーブル

このプロパティは読み取り専用です。

Variables プロパティに格納されている変数に関する情報。変数ごとに 1 つの行と次の列で構成される table として指定します。

列	説明
`Class`	変数のクラス。`'double'` や `'categorical'` などの文字ベクトルによる cell 配列を指定します。
`Range`	変数の範囲。ベクトルの cell 配列を指定します。連続変数 — 2 因子ベクトル `[min,max]`、最小値と最大値カテゴリカル変数 — 異なる変数値のベクトル
`InModel`	当てはめたモデルにどの変数が含まれているかを示すインジケーター。logical ベクトルを指定します。モデルに変数が含まれている場合、値は `true` です。
`IsCategorical`	カテゴリカル変数のインジケーター。logical ベクトルを指定します。変数がカテゴリカルである場合、値は `true` です。

VariableInfo には、モデルの当てはめに予測子または応答として使用されない変数もすべて含まれます。

データ型: table

`VariableNames` — 変数の名前
文字ベクトルの cell 配列

このプロパティは読み取り専用です。

変数の名前。文字ベクトルの cell 配列として指定します。このプロパティの要素は、モデルオブジェクトを作成するときに fitmnr の次のいずれかの引数で設定されます。

入力引数 Tbl で、予測子変数、応答、および使用されない変数の名前を指定します。
名前と値の引数 PredictorNames で、予測子変数の名前を指定します。
名前と値の引数 ResponseVarName で、応答変数の名前を指定します。

VariableNames には、モデルの当てはめに予測子または応答として使用されない変数もすべて含まれます。

データ型: cell

`Variables` — 入力データ
テーブル

このプロパティは読み取り専用です。

入力データ。table を指定します。Variables には予測子と応答の両方の値が格納されます。このプロパティの要素は、モデルオブジェクトを作成するときに fitmnr の次のいずれかの引数で設定されます。

X を指定した場合、X の列のすべての変数が Variables に格納されます。
Tbl を指定した場合、モデルの当てはめに予測子または応答データとして使用されない変数も含め、Tbl のすべての変数が Variables に格納されます。
Y を指定した場合、Y の応答データも Variables に格納されます。

データ型: table

オブジェクト関数

`coefCI`	多項回帰モデルの係数推定の信頼区間
`coefTest`	多項回帰モデルの係数に対する線形仮説検定
`feval`	各予測子について 1 つずつ入力を使用して多項回帰モデルの応答を予測
`partialDependence`	部分依存の計算
`plotPartialDependence`	部分依存プロット (PDP) および個別条件付き期待値 (ICE) プロットの作成
`plotResiduals`	多項回帰モデルの残差プロット
`plotSlice`	当てはめられた多項回帰面を通るスライスのプロット
`predict`	多項回帰モデルの応答を予測
`random`	当てはめられた多項回帰モデルからランダム応答を生成
`testDeviance`	多項回帰モデルの逸脱度検定

例

すべて折りたたむ

ノミナルモデルの係数の解析

ライブスクリプトを開く

標本データセット fisheriris を読み込みます。

load fisheriris

列ベクトル species には、3 種類のアヤメ (setosa、versicolor、virginica) が格納されています。行列 meas には、花に関する 4 種類の測定値、がく片の長さと幅 (cm) と花弁の長さと幅 (cm) が格納されています。

多項回帰モデルを当てはめ、測定値を使用してアヤメの種類を予測します。当てはめたモデルの Coefficients プロパティを使用して当てはめの結果を表示します。

MnrModel = fitmnr(meas,species);
MnrModel.Coefficients

ans=10×4 table
                               Value       SE       tStat       pValue  
                              _______    ______    _______    __________

    (Intercept_setosa)         2018.4    12.404     162.72             0
    x1_setosa                  673.85    3.5783     188.32             0
    x2_setosa                  -568.2     3.176     -178.9             0
    x3_setosa                 -516.44    3.5403    -145.87             0
    x4_setosa                 -2760.9    7.1203    -387.75             0
    (Intercept_versicolor)     42.638    5.2719     8.0878    6.0776e-16
    x1_versicolor              2.4652    1.1228     2.1956      0.028124
    x2_versicolor              6.6809    1.4789     4.5176    6.2559e-06
    x3_versicolor             -9.4294    1.2934    -7.2906     3.086e-13
    x4_versicolor             -18.286    2.0967    -8.7214    2.7476e-18

MnrModel は、ノミナル多項回帰モデルをデータに当てはめた結果を含む多項回帰モデルオブジェクトです。Coefficients プロパティに meas の各予測子の係数統計量が格納されています。列 pValue の "p" 値が小さく、すべての係数が 95% の信頼水準で統計的に有意であることを示しています。fitmnr では、species のカテゴリをそれらが最初に現れる順序で並べ替えます。既定では、その最後のカテゴリが基準カテゴリとなります。

並べ替え後の応答変数カテゴリの名前を表示するには、MnrModel の ClassNames プロパティを使用します。

MnrModel.ClassNames

ans = 3x1 cell
    {'setosa'    }
    {'versicolor'}
    {'virginica' }

出力から最後のカテゴリは 'virginica' であり、既定ではそれが基準カテゴリになります。

当てはめられた係数推定値の 95% 信頼区間を取得するには、オブジェクト関数 coefCI を呼び出します。

coefCI(MnrModel)

ans = 10×2
10³ ×

    1.9940    2.0428
    0.6668    0.6809
   -0.5745   -0.5620
   -0.5234   -0.5095
   -2.7749   -2.7469
    0.0323    0.0530
    0.0003    0.0047
    0.0038    0.0096
   -0.0120   -0.0069
   -0.0224   -0.0142

table Coefficients の Value 列の 10 個の係数について、それらの 95% 信頼区間が出力に表示されます。いずれの信頼区間もゼロと交差しておらず、すべての係数が 95% の信頼水準で対数オッズに影響することがわかります。

応答カテゴリの予測

ライブスクリプトを開く

標本データセット fisheriris を読み込みます。

load fisheriris

列ベクトル species には、3 種類のアヤメの種 (setosa、versicolor、virginica) が格納されています。行列 meas には、花に関する 4 種類の測定値、がく片の長さと幅 (cm) と花弁の長さと幅 (cm) が格納されています。

関数cvpartitionを使用して、種類と測定値のデータを学習データとテストデータに分割します。関数trainingを使用して、学習データの行のインデックスを取得します。

n = length(species);
partition = cvpartition(n,'Holdout',0.05);
idx_train = training(partition);

学習データの行のインデックスを使用して学習データを作成し、測定値の行列と種類のラベルのベクトルを作成します。

meastrain = meas(idx_train,:);
speciestrain = species(idx_train,:);

学習データを使用して多項回帰モデルを当てはめます。

mdl = fitmnr(meastrain,speciestrain)

mdl = 
Multinomial regression with nominal responses

                               Value       SE       tStat        pValue  
                              _______    ______    ________    __________

    (Intercept_setosa)         86.293    12.541      6.8807    5.9554e-12
    x1_setosa                 -1.0621    3.5795    -0.29673       0.76667
    x2_setosa                  23.851    3.1238      7.6352    2.2556e-14
    x3_setosa                 -27.266    3.5009     -7.7883    6.7894e-15
    x4_setosa                 -59.671    7.0214     -8.4985     1.921e-17
    (Intercept_versicolor)     42.637    5.2214      8.1659    3.1906e-16
    x1_versicolor              2.4652    1.1263      2.1887      0.028619
    x2_versicolor              6.6808     1.474      4.5325     5.829e-06
    x3_versicolor             -9.4292    1.2946     -7.2837     3.248e-13
    x4_versicolor             -18.286    2.0833     -8.7775     1.671e-18


143 observations, 276 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 302.0378, p-value = 1.5168e-60

mdl は、ノミナル多項回帰モデルをデータに当てはめた結果を含む多項回帰モデルオブジェクトです。meas の各予測子の係数統計量が table 出力に表示されます。既定では、virginica が fitmnr で基準カテゴリとして使用されます。

関数testを使用して、テストデータの行のインデックスを取得します。テストデータの行のインデックスを使用してテストデータを作成し、測定値の行列と種類のラベルのベクトルを作成します。

idx_test = test(partition);
meastest = meas(idx_test,:);
speciestest = species(idx_test,:);

meastest の測定値について、アヤメの種類を予測します。

speciespredict = predict(mdl,meastest)

speciespredict = 7x1 cell
    {'setosa'    }
    {'setosa'    }
    {'setosa'    }
    {'setosa'    }
    {'setosa'    }
    {'versicolor'}
    {'versicolor'}

speciespredict の予測を speciestest のカテゴリ名と比較します。

speciestest

speciestest = 7x1 cell
    {'setosa'    }
    {'setosa'    }
    {'setosa'    }
    {'setosa'    }
    {'setosa'    }
    {'versicolor'}
    {'versicolor'}

出力から、meastest の測定値について、アヤメの種類がモデルで正確に予測されていることがわかります。

エンジン気筒数の確率のプロット

ライブスクリプトを開く

標本データセット carbig を読み込みます。

load carbig;

ベクトル Acceleration および Displacement には、自動車の加速度と排気量のデータがそれぞれ格納されています。ベクトル Cylinders には、それぞれの自動車のエンジンに搭載された気筒の数のデータが格納されています。

Acceleration と Displacement を予測子変数、Cylinders を応答変数として使用して、順序多項回帰モデルを当てはめます。

MnrModel = fitmnr([Acceleration,Displacement],Cylinders,Model="ordinal",...
    PredictorNames=["Acceleration" "Displacement"])

MnrModel = 
Multinomial regression with ordinal responses

                       Value         SE        tStat       pValue  
                     _________    ________    _______    __________

    (Intercept_3)       11.949      3.1817     3.7555    0.00017299
    (Intercept_4)        27.08      4.9481     5.4727    4.4321e-08
    (Intercept_5)       27.528      4.9738     5.5346    3.1195e-08
    (Intercept_6)       45.346      7.8292     5.7919    6.9593e-09
    Acceleration     -0.063533      0.1041    -0.6103       0.54167
    Displacement      -0.16731    0.027885         -6    1.9726e-09


406 observations, 1618 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 786.5846, p-value = 1.5679e-171

MnrModel は、順序多項回帰モデルをデータに当てはめた結果を含む多項回帰モデルオブジェクトです。各予測子変数の係数統計量が table 出力に表示されます。列 pValue の "p" 値が小さく、Acceleration 項の係数が統計的に有意であると結論付けるだけの十分な証拠はないことを示しています。一方、Displacement については、99% の信頼水準で統計的に有意な影響を与えると結論付けるだけの十分な証拠があります。

ClassNames プロパティを使用して、自動車のエンジン気筒数の取り得る数を表示します。

MnrModel.ClassNames

既定では、出力の最後のカテゴリが基準カテゴリとなります。出力から、基準カテゴリは 8 気筒エンジンを搭載した自動車に対応することがわかります。

plotSlice を使用して、予測子変数 Displacement の値を変化させて、それぞれの気筒数の自動車である確率の積み上げヒストグラムをプロットします。既定では、Acceleration の値については、その学習データの平均に plotSlice で固定されます。

plotSlice(MnrModel,"stackedhist",PredictorToVary="Displacement")
hold on
lgd = legend;
title(lgd, "Number of cylinders");

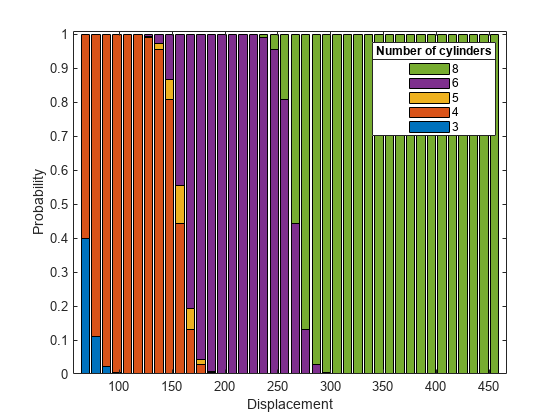
Figure contains an axes object. The axes object with xlabel Displacement, ylabel Probability contains 5 objects of type bar. These objects represent 3, 4, 5, 6, 8.

プロットから、自動車の排気量が増えるほど、より多くの気筒を搭載した自動車である確率が高くなることがわかります。これは、モデルの Displacement 項の "p" 値が小さいことと整合します。

自動車の排気量が基準カテゴリの確率に与える影響の分析

ライブスクリプトを開く

標本データセット carbig を読み込みます。

load carbig;

Acceleration と Displacement を予測子変数、Cylinders を応答変数として使用して、順序多項回帰モデルを当てはめます。

MnrModel = fitmnr([Acceleration,Displacement],Cylinders,Model="ordinal",...
    PredictorNames=["Acceleration" "Displacement"])

MnrModel = 
Multinomial regression with ordinal responses

                       Value         SE        tStat       pValue  
                     _________    ________    _______    __________

    (Intercept_3)       11.949      3.1817     3.7555    0.00017299
    (Intercept_4)        27.08      4.9481     5.4727    4.4321e-08
    (Intercept_5)       27.528      4.9738     5.5346    3.1195e-08
    (Intercept_6)       45.346      7.8292     5.7919    6.9593e-09
    Acceleration     -0.063533      0.1041    -0.6103       0.54167
    Displacement      -0.16731    0.027885         -6    1.9726e-09


406 observations, 1618 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 786.5846, p-value = 1.5679e-171

MnrModel は、順序多項回帰モデルをデータに当てはめた結果を含む多項回帰モデルオブジェクトです。それぞれの予測子変数の係数統計量が table 出力に表示されます。列 pValue の "p" 値が小さく、Acceleration 項の係数が統計的に有意であると結論付けるだけの十分な証拠はないことを示しています。一方、Displacement については、99% の信頼水準で統計的に有意な影響を与えると結論付けるだけの十分な証拠があります。

ClassNames プロパティを使用して、自動車のエンジン気筒数の取り得る数を表示します。

MnrModel.ClassNames

基準カテゴリは 8 気筒エンジンを搭載した自動車に対応します。

オブジェクト関数plotPartialDependenceを使用して、基準カテゴリの確率の Displacement 予測子に対する部分依存をプロットします。

plotPartialDependence(MnrModel,2,8)

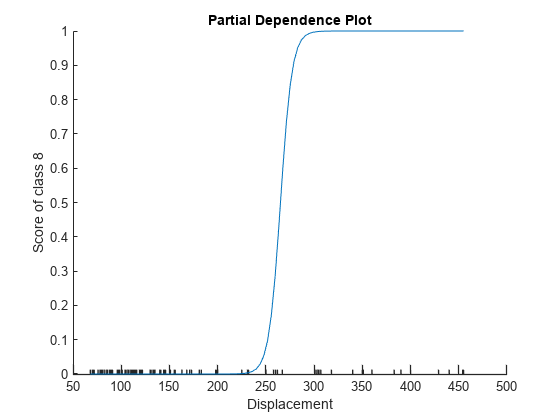
Figure contains an axes object. The axes object with title Partial Dependence Plot, xlabel Displacement, ylabel Score of class 8 contains an object of type line.

プロットから、Displacement の値が約 250 に達したところで、基準カテゴリの自動車である確率が急激に高くなることがわかります。

詳細

すべて展開する

逸脱度

逸脱度は、残差二乗和を汎化したものです。飽和モデルと比較した適合度を測定します。

モデル M₁ の逸脱度は、モデル M₁ の対数尤度と飽和モデル M_s の対数尤度の差の 2 倍です。飽和モデルは、推定可能な最大数のパラメーターを含むモデルです。

たとえば、応答の値が異なる可能性がある n 個の観測値 y_i (i = 1, 2, ..., n) がある場合、それらの応答を完全に予測する飽和モデル (n 個のパラメーターを使用) を定義できます。L(b,y) がパラメーター b をもつモデルの尤度関数の最大値を示しているものとします。この場合、モデル M₁ の逸脱度は以下のようになります。

$- 2 (\log L (b_{1}, y) - \log L (b_{S}, y)),$

ここで、b₁ および b_s には、それぞれモデル M₁ および飽和モデルの推定パラメーターが含まれます。逸脱度は自由度 n – p のカイ二乗分布になります。ここで、n は飽和モデルのパラメーター数、p はモデル M₁ のパラメーター数です。

2 つの異なる多項回帰モデル M₁ および M₂ があり、M₁ は M₂ 内の項のサブセットをもつと仮定します。モデルの当てはめは 2 つのモデルの逸脱度 D₁ と D₂ を比較することによって評価できます。逸脱度の差異は以下のとおりです。

$\begin{array}{l} D = D_{2} - D_{1} = - 2 (\log L (b_{2}, y) - \log L (b_{S}, y)) + 2 (\log L (b_{1}, y) - \log L (b_{S}, y)) \\ = - 2 (\log L (b_{2}, y) - \log L (b_{1}, y)) . \end{array}$

差異 D は漸近的にカイ二乗分布となりますが、その自由度 v は、M₁ および M₂ で推定されたパラメーター数の差異に等しくなります。この検定の p 値は 1 – chi2cdf(D,v,"upper") を使用して取得できます。

通常は、定数項をもち予測子をもたないモデル M₂ を使用して D を調べます。そのため、D は自由度が p – 1 のカイ二乗分布となります。分散を推定する場合、推定された分散で除算した差異は、分子の自由度が p – 1、分母の自由度が n – p の F 分布となります。

参照

[1] Allison, P. D. "Measures of Fit for Logistic Regression." Statistical Horizons LLC and the University of Pennsylvania, 2014.

[2] McCullagh, P., and J. A. Nelder. Generalized Linear Models. New York: Chapman & Hall, 1990.

[3] Long, J. S. Regression Models for Categorical and Limited Dependent Variables. Sage Publications, 1997.

[4] Dobson, A. J., and A. G. Barnett. An Introduction to Generalized Linear Models. Chapman and Hall/CRC. Taylor & Francis Group, 2008.

バージョン履歴

R2023a で導入

参考

fitmnr | fitglm | GeneralizedLinearModel

MultinomialRegression

説明

作成

プロパティ

係数推定値

ClassNames — 応答変数カテゴリの名前 categorical 配列 | 文字配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

CoefficientCovariance — モデルの係数の共分散行列 (p+1) 行 (p+1) 列の数値の行列

CoefficientNames — 係数の名前 文字ベクトルの cell 配列

Coefficients — 係数の値 テーブル

IncludeClassInteractions — 応答カテゴリと係数の間の交互作用を表すインジケーター true または 1 | false または 0

Link — リンク関数 'logit' | 'probit' | 'comploglog' | 'loglog'

ModelType — モデルのタイプ 'nominal' | 'ordinal' | 'hierarchical'

NumCoefficients — モデルの係数の数 正の整数

要約統計量

Deviance — 当てはめの逸脱度 数値

DFE — 誤差に対する自由度 正の整数

Dispersion — 分散 数値スカラー

EstimateDispersion — 分散を推定するかどうかを示すインジケーター false | true

Fitted — 入力データを基に当てはめを行った応答値 categorical 配列 | 文字配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

LogLikelihood — 当てはめたモデルの対数尤度 数値

ModelCriterion — モデルの比較基準 構造体

Residuals — 当てはめたモデルの残差 テーブル

Rsquared — 当てはめたモデルの疑似決定係数の値 構造体

入力データ

Formula — 回帰モデル LinearFormula オブジェクト

NumObservations — 観測値の数 正の整数

NumPredictors — 予測子変数の数 正の整数

NumVariables — 変数の数 正の整数

ObservationInfo — 観測値の情報 n 行 3 列の table

ObservationNames — 観測値の名前 文字ベクトルの cell 配列

PredictorNames — モデルの当てはめに使用した予測子の名前 文字ベクトルの cell 配列

ResponseName — 応答変数名 文字ベクトル

VariableInfo — 変数に関する情報 テーブル

VariableNames — 変数の名前 文字ベクトルの cell 配列

Variables — 入力データ テーブル

オブジェクト関数

例

ノミナル モデルの係数の解析

応答カテゴリの予測

エンジン気筒数の確率のプロット

自動車の排気量が基準カテゴリの確率に与える影響の分析

詳細

逸脱度

参照

バージョン履歴

参考

トピック

`ClassNames` — 応答変数カテゴリの名前
categorical 配列 | 文字配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

`CoefficientCovariance` — モデルの係数の共分散行列
(p+1) 行 (p+1) 列の数値の行列

`CoefficientNames` — 係数の名前
文字ベクトルの cell 配列

`Coefficients` — 係数の値
テーブル

`IncludeClassInteractions` — 応答カテゴリと係数の間の交互作用を表すインジケーター
`true` または `1` | `false` または `0`

`Link` — リンク関数
`'logit'` | `'probit'` | `'comploglog'` | `'loglog'`

`ModelType` — モデルのタイプ
`'nominal'` | `'ordinal'` | `'hierarchical'`

`NumCoefficients` — モデルの係数の数
正の整数

`Deviance` — 当てはめの逸脱度
数値

`DFE` — 誤差に対する自由度
正の整数

`Dispersion` — 分散
数値スカラー

`EstimateDispersion` — 分散を推定するかどうかを示すインジケーター
`false` | `true`

`Fitted` — 入力データを基に当てはめを行った応答値
categorical 配列 | 文字配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

`LogLikelihood` — 当てはめたモデルの対数尤度
数値

`ModelCriterion` — モデルの比較基準
構造体

`Residuals` — 当てはめたモデルの残差
テーブル

`Rsquared` — 当てはめたモデルの疑似決定係数の値
構造体

`Formula` — 回帰モデル
`LinearFormula` オブジェクト

`NumObservations` — 観測値の数
正の整数

`NumPredictors` — 予測子変数の数
正の整数

`NumVariables` — 変数の数
正の整数

`ObservationInfo` — 観測値の情報
n 行 3 列の table

`ObservationNames` — 観測値の名前
文字ベクトルの cell 配列

`PredictorNames` — モデルの当てはめに使用した予測子の名前
文字ベクトルの cell 配列

`ResponseName` — 応答変数名
文字ベクトル

`VariableInfo` — 変数に関する情報
テーブル

`VariableNames` — 変数の名前
文字ベクトルの cell 配列

`Variables` — 入力データ
テーブル

ノミナルモデルの係数の解析