機械学習モデルの解釈

このトピックでは、モデルを解釈するための Statistics and Machine Learning Toolbox™ の機能について説明し、機械学習モデル (分類および回帰) を解釈する方法を示します。

機械学習モデルは、そのモデルでどのように予測が行われるかがわかりにくいことがあるため、"ブラックボックス" モデルとよく呼ばれます。解釈可能性ツールを使用すると、機械学習アルゴリズムのこの側面に対処でき、予測子が予測にどのように寄与しているか (または寄与していないか) がわかります。また、モデルがその予測で正しい証拠を使用しているかどうかを検証でき、すぐにはわからないモデルバイアスを検出できます。

モデルを解釈するための機能

lime、shapley および plotPartialDependence を使用して、学習済みの分類モデルまたは回帰モデルの予測に対する個々の予測子の寄与を説明します。

lime — Local Interpretable Model-agnostic Explanations (LIME [1]) は、解釈可能な単純モデルをクエリ点に当てはめることにより、クエリ点についての予測を解釈します。単純モデルは学習済みモデルの近似として動作し、クエリ点周辺のモデル予測を説明します。単純モデルにできるのは、線形モデルまたは決定木モデルのいずれかです。線形モデルの推定係数または決定木モデルの予測子の推定重要度を使用して、クエリ点についての予測に対する個々の予測子の寄与を説明できます。詳細については、LIMEを参照してください。
shapley — クエリ点の予測子のシャープレイ値 ([2]、[3]、[4]) は、クエリ点についての予測 (回帰の場合は応答、分類の場合はクラススコア) に関して予測子が原因で生じた平均予測からの偏差を説明します。クエリ点について、すべての特徴量に関するシャープレイ値の合計は、予測の平均からの合計偏差に対応します。詳細については、機械学習モデルのシャープレイ値を参照してください。
plotPartialDependence および partialDependence — 部分依存プロット (PDP [5]) は、学習済みモデルにおける予測子 (または予測子のペア) と予測 (回帰の場合は応答、分類の場合はクラススコア) の関係を示します。選択した予測子に対する部分依存は、他の変数の効果を除外することで取得した平均予測によって定義されます。そのため、部分依存は、データセットに対する選択した予測子の平均効果を示す、選択した予測子の関数です。各観測値について一連の個別条件付き期待値 (ICE [6]) プロットを作成して、単一の観測値に対する選択した予測子の効果を示すこともできます。詳細については、plotPartialDependence のリファレンスページの詳細を参照してください。

一部の機械学習モデルでは、モデルの学習プロセスの一部としてモデルが予測子の重要度を学習する組み込み型特徴選択がサポートされます。予測子の推定重要度を使用してモデル予測を説明できます。以下に例を示します。

バギングされた決定木 (ランダムフォレストなど) のアンサンブル (ClassificationBaggedEnsemble または RegressionBaggedEnsemble) に学習をさせて関数 predictorImportance および oobPermutedPredictorImportance を使用します。
重要度が最も低い予測子の係数を縮小する LASSO 正則化を使用して線形モデルに学習をさせます。その後、推定係数を予測子の重要度の測定値として使用します。たとえば、fitclinear または fitrlinear を使用して名前と値の引数 'Regularization' を 'lasso' として指定します。

組み込み型特徴選択をサポートする機械学習モデルの一覧については、組み込み型特徴選択を参照してください。

モデルの解釈にはローカル、コーホート、グローバルの 3 つのレベルがあり、それぞれに応じて Statistics and Machine Learning Toolbox 機能を使用します。

レベル	目的	使用例	Statistics and Machine Learning Toolbox 機能
ローカルな解釈	単一のクエリ点についての予測を説明する。	個々の予測の重要な予測子を識別する。直観的ではない予測を調べる。	指定したクエリ点に対して `lime` と `shapley` を使用します。
コーホート解釈	学習済みモデルがデータセット全体のサブセットについてどのように予測を行うかを説明する。	特定の標本グループについての予測を検証する。	複数のクエリ点に対して `lime` と `shapley` を使用します。`lime` オブジェクトまたは `shapley` オブジェクトの作成後、オブジェクト関数 `fit` を複数回呼び出して他のクエリ点についての予測を解釈できます。 `lime`、`shapley` および `plotPartialDependence` を呼び出す際にデータのサブセットを渡します。これらの機能は、学習データセット全体ではなく指定されたサブセットを使用して学習済みモデルを解釈します。
グローバルな解釈	学習済みモデルがデータセット全体についてどのように予測を行うかを説明する。	学習済みモデルがどのように機能するかを示す。異なるモデルを比較する。	`plotPartialDependence` を使用して、対象の予測子の PDP と ICE プロットを作成します。 `shapley` を使用して、すべての観測値のシャープレイ値を計算します。オブジェクト関数 `plot`、`boxchart`、または `swarmchart` を使用して結果を可視化します。組み込み型特徴選択をサポートする学習済みモデルから重要な予測子を見つけます。

分類モデルの解釈

ライブスクリプトを開く

この例では、ランダムフォレストアルゴリズムを使用してバギングされた決定木のアンサンブルに学習をさせ、解釈可能性機能を使用して学習済みモデルを解釈します。学習済みモデルのオブジェクト関数 (oobPermutedPredictorImportanceおよびpredictorImportance) を使用してモデル内の重要な予測子を見つけます。また、limeとshapleyを使用して指定したクエリ点についての予測を解釈します。その後、plotPartialDependenceを使用して、重要な予測子と予測分類スコアの関係を示すプロットを作成します。

アンサンブル分類モデルの学習

CreditRating_Historical データセットを読み込みます。データセットには、顧客 ID、顧客の財務比率、業種ラベル、および信用格付けが格納されています。

tbl = readtable('CreditRating_Historical.dat');

テーブルの最初の 3 行を表示します。

head(tbl,3)

     ID      WC_TA    RE_TA    EBIT_TA    MVE_BVTD    S_TA     Industry    Rating
    _____    _____    _____    _______    ________    _____    ________    ______

    62394    0.013    0.104     0.036      0.447      0.142       3        {'BB'}
    48608    0.232    0.335     0.062      1.969      0.281       8        {'A' }
    42444    0.311    0.367     0.074      1.935      0.366       1        {'A' }

tbl から顧客 ID と信用格付けを含む列を削除して、予測子変数の table を作成します。

tblX = removevars(tbl,["ID","Rating"]);

関数fitcensembleを使用してアンサンブル集約法としてランダムフォレスト ('Bag') を指定することで、バギングされた決定木のアンサンブルに学習をさせます。ランダムフォレストアルゴリズムの再現性を得るため、木学習器の名前と値の引数 'Reproducible' を true に指定します。また、クラス名を指定して学習済みモデルのクラスの順序を設定します。

rng('default') % For reproducibility
t = templateTree('Reproducible',true);
blackbox = fitcensemble(tblX,tbl.Rating, ...
    'Method','Bag','Learners',t, ...
    'CategoricalPredictors','Industry', ...
    'ClassNames',{'AAA' 'AA' 'A' 'BBB' 'BB' 'B' 'CCC'});

blackbox はClassificationBaggedEnsembleモデルです。

モデル固有の解釈可能性機能の使用

ClassificationBaggedEnsemble は、学習済みモデル内の重要な予測子を見つける 2 つのオブジェクト関数oobPermutedPredictorImportanceおよびpredictorImportanceをサポートします。

関数 oobPermutedPredictorImportance を使用して out-of-bag 予測子の重要度を推定します。1 予測子ごとに out-of-bag データが無作為に並べ替えられ、この並べ替えによる out-of-bag 誤差の増加が推定されます。増加がより大きいほど、特徴はより重要になります。

Imp1 = oobPermutedPredictorImportance(blackbox);

関数 predictorImportance を使用して予測子の重要度を推定します。この関数は、各予測子について分割によるノードリスク変動を合計し、この合計を枝ノード数で除算することにより、予測子の重要度を推定します。

Imp2 = predictorImportance(blackbox);

予測子の重要度の推定を格納する table を作成し、その table を使用して横棒グラフを作成します。予測子名に含まれるアンダースコアを表示するには、座標軸の TickLabelInterpreter 値を 'none' に変更します。

table_Imp = table(Imp1',Imp2', ...
    'VariableNames',{'Out-of-Bag Permuted Predictor Importance','Predictor Importance'}, ...
    'RowNames',blackbox.PredictorNames);
tiledlayout(1,2)
ax1 = nexttile;
table_Imp1 = sortrows(table_Imp,'Out-of-Bag Permuted Predictor Importance');
barh(categorical(table_Imp1.Row,table_Imp1.Row),table_Imp1.('Out-of-Bag Permuted Predictor Importance'))
xlabel('Out-of-Bag Permuted Predictor Importance')
ylabel('Predictor')
ax2 = nexttile;
table_Imp2 = sortrows(table_Imp,'Predictor Importance');
barh(categorical(table_Imp2.Row,table_Imp2.Row),table_Imp2.('Predictor Importance'))
xlabel('Predictor Importance')
ax1.TickLabelInterpreter = 'none';
ax2.TickLabelInterpreter = 'none';

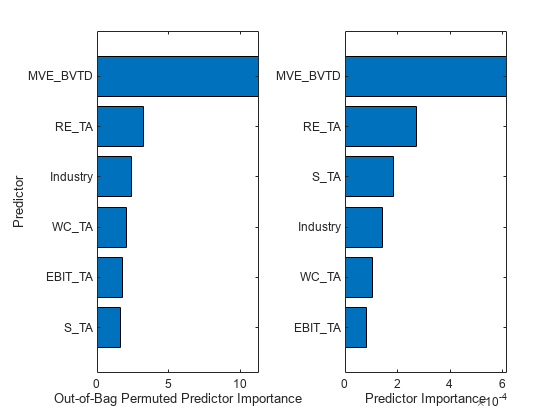
Figure contains 2 axes objects. Axes object 1 with xlabel Out-of-Bag Permuted Predictor Importance, ylabel Predictor contains an object of type bar. Axes object 2 with xlabel Predictor Importance contains an object of type bar.

両方のオブジェクト関数で MVE_BVTD および RE_TA が上位 2 つの重要な予測子として識別されています。

クエリ点の指定

Rating が 'AAA' である観測値を特定して、その中から 4 つのクエリ点を選択します。

rng('default')
tblX_AAA = tblX(strcmp(tbl.Rating,'AAA'),:);
queryPoint = datasample(tblX_AAA,4,'Replace',false)

queryPoint=4×6 table
    WC_TA    RE_TA    EBIT_TA    MVE_BVTD    S_TA     Industry
    _____    _____    _______    ________    _____    ________

    0.283    0.715     0.069      9.612      1.066       11   
    0.603    0.891     0.117      7.851      0.591        6   
    0.212    0.486     0.057      3.986      0.679        2   
    0.273    0.491     0.071      3.287      0.465        5

線形単純モデルでの LIME の使用

線形単純モデルでlime を使用してクエリ点についての予測を説明します。lime は合成データセットを生成し、その合成データセットに単純モデルを当てはめます。

tblX_AAA を使用して lime オブジェクトを作成し、lime がデータセット全体ではなく Rating が 'AAA' である観測値のみを使用して合成データセットを生成するようにします。

explainer_lime = lime(blackbox,tblX_AAA);

lime のDataLocalityの既定値は 'global' です。この場合、lime は既定でグローバルな合成データセットを生成し、すべてのクエリ点に使用します。lime は異なる観測値の重みを使用して、クエリ点に近い観測値ほど重み値の比重が大きくなるようにします。そのため、各単純モデルを特定のクエリ点に対する学習済みモデルの近似として解釈できます。

オブジェクト関数fitを使用して、4 つのクエリ点に単純モデルを当てはめます。3 番目の入力 (単純モデルで使用する重要な予測子の数) を 6 に指定して、6 つすべての予測子を使用します。

explainer_lime1 = fit(explainer_lime,queryPoint(1,:),6);
explainer_lime2 = fit(explainer_lime,queryPoint(2,:),6);
explainer_lime3 = fit(explainer_lime,queryPoint(3,:),6);
explainer_lime4 = fit(explainer_lime,queryPoint(4,:),6);

オブジェクト関数plotを使用して、単純モデルの係数をプロットします。

tiledlayout(2,2)
nexttile
plot(explainer_lime1)
nexttile
plot(explainer_lime2)
nexttile
plot(explainer_lime3)
nexttile
plot(explainer_lime4)

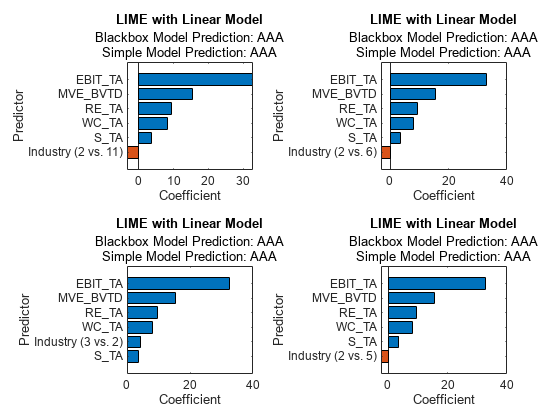
すべての単純モデルで EBIT_TA、MVE_BVTD、RE_TA、および WC_TA が上位 4 つの重要な予測子として識別されています。予測子の正の係数は、予測子の値を大きくすると単純モデルの予測スコアが大きくなることを示しています。

カテゴリカル予測子の場合、関数 plot ではそのカテゴリカル予測子の最も重要なダミー変数のみが表示されます。そのため、棒グラフごとに異なるダミー変数が表示されます。

シャープレイ値の計算

クエリ点の予測子のシャープレイ値は、クエリ点についての予測スコアに関して予測子が原因で生じた平均スコアからの偏差を説明します。tblX_AAA を使用して shapley オブジェクトを作成し、shapley が 'AAA' の標本に基づいて期待される寄与を計算するようにします。

explainer_shapley = shapley(blackbox,tblX_AAA);

オブジェクト関数fitを使用して、クエリ点のシャープレイ値を計算します。

explainer_shapley1 = fit(explainer_shapley,queryPoint(1,:));
explainer_shapley2 = fit(explainer_shapley,queryPoint(2,:));
explainer_shapley3 = fit(explainer_shapley,queryPoint(3,:));
explainer_shapley4 = fit(explainer_shapley,queryPoint(4,:));

オブジェクト関数plotを使用して、シャープレイ値をプロットします。

tiledlayout(2,2)
nexttile
plot(explainer_shapley1)
nexttile
plot(explainer_shapley2)
nexttile
plot(explainer_shapley3)
nexttile
plot(explainer_shapley4)

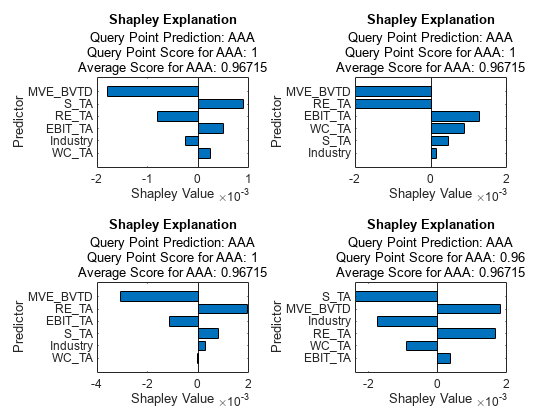
すべてのクエリ点の最も重要な予測子は MVE_BVTD です。MVE_BVTD のシャープレイ値は最初の 3 つのクエリ点で正になっています。クエリ点の変数 MVE_BVTD の値は、約 9.6、7.9、4.0、および 3.3 です。4 つのクエリ点のシャープレイ値によると、MVE_BVTD の値が大きいと予測スコアが平均と比較して大きくなり、MVE_BVTD の値が小さいと予測スコアが小さくなります。

部分依存プロット (PDP) の作成

PDP プロットは、学習済みモデルにおける予測子と予測スコアの平均化された関係を示します。RE_TA および MVE_BVTD の PDP を作成し、他の解釈可能性ツールで重要な予測子として識別します。tblx_AAA を plotPartialDependence に渡して、この関数が 'AAA' の標本のみを使用して予測スコアの期待値を計算するようにします。

figure
plotPartialDependence(blackbox,'RE_TA','AAA',tblX_AAA)

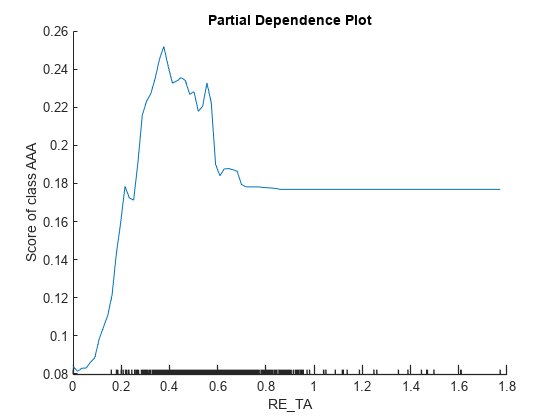
Figure contains an axes object. The axes object with title Partial Dependence Plot, xlabel R E indexOf T baseline A RE_TA, ylabel Score of class AAA contains an object of type line.

plotPartialDependence(blackbox,'MVE_BVTD','AAA',tblX_AAA)

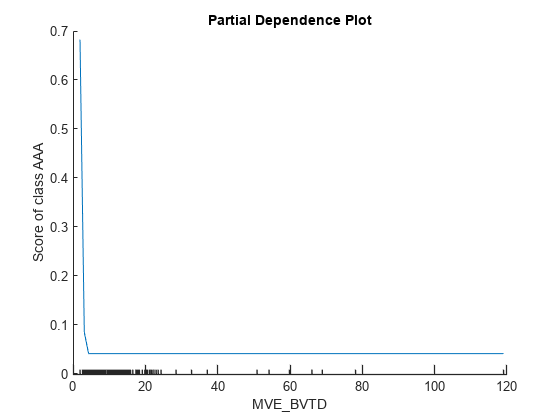
Figure contains an axes object. The axes object with title Partial Dependence Plot, xlabel M V E indexOf B baseline V T D MVE_BVTD, ylabel Score of class AAA contains an object of type line.

x 軸の小目盛りは tbl_AAA の一意の予測子値を表します。MVE_BVTD のプロットは、MVE_BVTD の値が小さいと予測スコアが大きくなることを示しています。MVE_BVTD の値が約 5 に達するまではその値が大きくなるとスコア値は小さくなり、その後は MVE_BVTD の値が大きくなってもスコア値は変化しないままとなります。plotPartialDependence で識別されたサブセット tbl_AAA における MVE_BVTD に対する依存関係は、lime と shapley で識別された 4 つのクエリ点における MVE_BVTD のローカルな寄与と一致しません。

回帰モデルの解釈

ライブスクリプトを開く

回帰問題に関するモデルの解釈ワークフローは、分類モデルの解釈の例で示した分類問題に関するワークフローに似ています。

この例では、ガウス過程回帰 (GPR) モデルに学習をさせ、解釈可能性機能を使用して学習済みモデルを解釈します。GPR モデルのカーネルパラメーターを使用して予測子の重みを推定します。また、limeとshapleyを使用して指定したクエリ点についての予測を解釈します。その後、plotPartialDependenceを使用して、重要な予測子と予測応答の関係を示すプロットを作成します。

GPR モデルの学習

carbig データセットを読み込みます。このデータセットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。

load carbig

予測子変数 Acceleration、Cylinders などを格納する table を作成します。

tbl = table(Acceleration,Cylinders,Displacement,Horsepower,Model_Year,Weight);

関数 fitrgp を使用して、応答変数 MPG の GPR モデルに学習をさせます。KernelFunction として 'ardsquaredexponential' を指定して、予測子ごとに長さスケールが異なる二乗指数カーネルを使用します。

blackbox = fitrgp(tbl,MPG,'ResponseName','MPG','CategoricalPredictors',[2 5], ...
    'KernelFunction','ardsquaredexponential');

blackbox はRegressionGPモデルです。

モデル固有の解釈可能性機能の使用

モデルで使用されるカーネル関数の学習済み長さスケールから予測子の重み (予測子の重要度) を計算できます。長さスケールは、予測子がどのくらい応答値から離れると無相関になるかを定義します。負の学習済み長さスケールの指数を使用して、正規化した予測子の重みを求めます。

sigmaL = blackbox.KernelInformation.KernelParameters(1:end-1); % Learned length scales
weights = exp(-sigmaL); % Predictor weights
weights = weights/sum(weights); % Normalized predictor weights

正規化した予測子の重みを格納する table を作成し、その table を使用して横棒グラフを作成します。予測子名に含まれるアンダースコアを表示するには、座標軸の TickLabelInterpreter 値を 'none' に変更します。

tbl_weight = table(weights,'VariableNames',{'Predictor Weight'}, ...
    'RowNames',blackbox.ExpandedPredictorNames);
tbl_weight = sortrows(tbl_weight,'Predictor Weight');
b = barh(categorical(tbl_weight.Row,tbl_weight.Row),tbl_weight.('Predictor Weight'));
b.Parent.TickLabelInterpreter = 'none'; 
xlabel('Predictor Weight')
ylabel('Predictor')

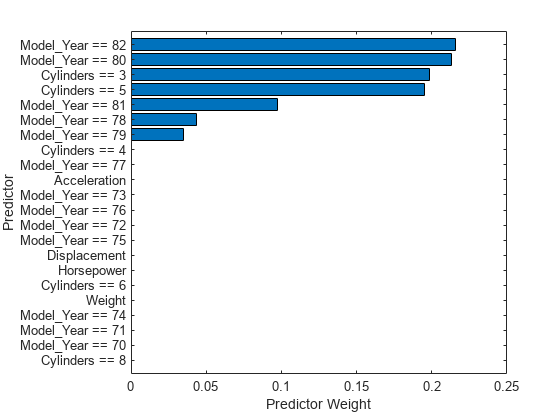
Figure contains an axes object. The axes object with xlabel Predictor Weight, ylabel Predictor contains an object of type bar.

予測子の重みから、カテゴリカル予測子 Model_Year および Cylinders の複数のダミー変数が重要であることがわかります。

クエリ点の指定

MPG の値が MPG の 0.25 分位数より小さい観測値を特定します。サブセットから、欠損値が含まれていない 4 つのクエリ点を選択します。

rng('default') % For reproducibility
idx_subset = find(MPG < quantile(MPG,0.25));
tbl_subset = tbl(idx_subset,:);
queryPoint = datasample(rmmissing(tbl_subset),4,'Replace',false)

queryPoint=4×6 table
    Acceleration    Cylinders    Displacement    Horsepower    Model_Year    Weight
    ____________    _________    ____________    __________    __________    ______

        13.2            8            318            150            76         3940 
        14.9            8            302            130            77         4295 
          14            8            360            215            70         4615 
        13.7            8            318            145            77         4140

単純な木モデルでの LIME の使用

単純な決定木モデルでlimeを使用してクエリ点についての予測を説明します。lime は合成データセットを生成し、その合成データセットに単純モデルを当てはめます。

tbl_subset を使用して lime オブジェクトを作成し、lime がデータセット全体ではなくサブセットを使用して合成データセットを生成するようにします。SimpleModelType として 'tree' を指定して、単純な決定木モデルを使用します。

explainer_lime = lime(blackbox,tbl_subset,'SimpleModelType','tree');

オブジェクト関数fitを使用して、4 つのクエリ点に単純モデルを当てはめます。3 番目の入力 (単純モデルで使用する重要な予測子の数) を 6 に指定します。この設定により、ソフトウェアは、決定分岐 (枝ノード) の最大数を 6 に指定し、当てはめられた決定木が、総数を上限に予測子を使用するようにします。

explainer_lime1 = fit(explainer_lime,queryPoint(1,:),6);
explainer_lime2 = fit(explainer_lime,queryPoint(2,:),6);
explainer_lime3 = fit(explainer_lime,queryPoint(3,:),6);
explainer_lime4 = fit(explainer_lime,queryPoint(4,:),6);

オブジェクト関数plot を使用して、予測子の重要度をプロットします。

tiledlayout(2,2)
nexttile
plot(explainer_lime1)
nexttile
plot(explainer_lime2)
nexttile
plot(explainer_lime3)
nexttile
plot(explainer_lime4)

すべての単純モデルで Displacement、Model_Year および Weight が重要な予測子として識別されています。

シャープレイ値の計算

クエリ点の予測子のシャープレイ値は、クエリ点についての予測応答に関して予測子が原因で生じた平均応答からの偏差を説明します。tbl_subset を使用してモデル blackbox の shapley オブジェクトを作成し、shapley が tbl_subset の観測値に基づいて期待される寄与を計算するようにします。

explainer_shapley = shapley(blackbox,tbl_subset);

オブジェクト関数fitを使用して、クエリ点のシャープレイ値を計算します。

explainer_shapley1 = fit(explainer_shapley,queryPoint(1,:));
explainer_shapley2 = fit(explainer_shapley,queryPoint(2,:));
explainer_shapley3 = fit(explainer_shapley,queryPoint(3,:));
explainer_shapley4 = fit(explainer_shapley,queryPoint(4,:));

オブジェクト関数plotを使用して、シャープレイ値をプロットします。

tiledlayout(2,2)
nexttile
plot(explainer_shapley1)
nexttile
plot(explainer_shapley2)
nexttile
plot(explainer_shapley3)
nexttile
plot(explainer_shapley4)

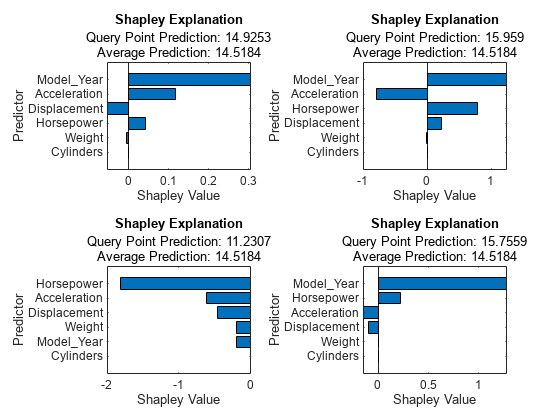
Model_Year は 1 番目、2 番目および 4 番目のクエリ点で最も重要な予測子であり、Model_Year のシャープレイ値は 3 つのクエリ点では正です。変数 Model_Year の値は、これら 3 つの点では 76 または 77、3 番目のクエリ点では 70 です。4 つのクエリ点のシャープレイ値によると、Model_Year の値が小さいと予測応答が平均と比較して小さくなり、Model_Year の値が大きいと予測応答が大きくなります。

部分依存プロット (PDP) の作成

PDP プロットは、学習済みモデルにおける予測子と予測応答の平均化された関係を示します。他の解釈可能性ツールで重要な予測子として識別された Model_Year の PDP を作成します。tbl_subset を plotPartialDependence に渡して、この関数が tbl_subset の標本のみを使用して予測応答の期待値を計算するようにします。

figure
plotPartialDependence(blackbox,'Model_Year',tbl_subset)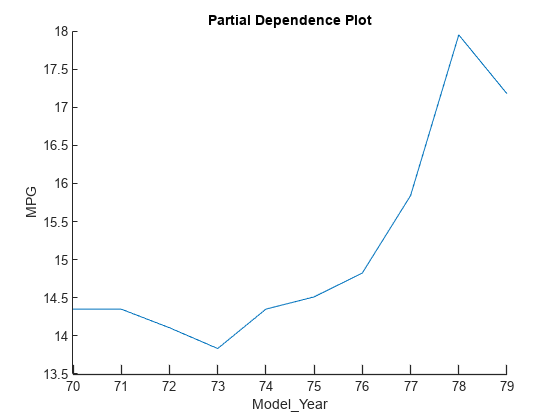

Figure contains an axes object. The axes object with title Partial Dependence Plot, xlabel M o d e l indexOf Y baseline e a r Model_Year, ylabel MPG contains an object of type line.

プロットには、4 つのクエリ点のシャープレイ値で識別されたものと同じトレンドが表示されます。Model_Year の値が大きくなると予測応答 (MPG) の値も大きくなります。

参照

[1] Ribeiro, Marco Tulio, S. Singh, and C. Guestrin. "'Why Should I Trust You?': Explaining the Predictions of Any Classifier." In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1135–44. San Francisco, California: ACM, 2016.

[2] Lundberg, Scott M., and S. Lee. "A Unified Approach to Interpreting Model Predictions." Advances in Neural Information Processing Systems 30 (2017): 4765–774.

[3] Aas, Kjersti, Martin Jullum, and Anders Løland. "Explaining Individual Predictions When Features Are Dependent: More Accurate Approximations to Shapley Values." Artificial Intelligence 298 (September 2021).

[4] Lundberg, Scott M., G. Erion, H. Chen, et al. "From Local Explanations to Global Understanding with Explainable AI for Trees." Nature Machine Intelligence 2 (January 2020): 56–67.

[5] Friedman, Jerome. H. “Greedy Function Approximation: A Gradient Boosting Machine.” The Annals of Statistics 29, no. 5 (2001): 1189-1232.

[6] Goldstein, Alex, Adam Kapelner, Justin Bleich, and Emil Pitkin. “Peeking Inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation.” Journal of Computational and Graphical Statistics 24, no. 1 (January 2, 2015): 44–65.

参考

lime | shapley | plotPartialDependence