fit

Local Interpretable Model-agnostic Explanations (LIME) の単純モデルの当てはめ

R2020b 以降

構文

newresults = fit(results,queryPoint,numImportantPredictors)

newresults = fit(results,queryPoint,numImportantPredictors,Name,Value)

説明

newresults = fit(results,queryPoint,numImportantPredictors) は、指定された数 (numImportantPredictors) の重要な予測子を使用して、指定されたクエリ点 (queryPoint) に新しい単純モデルを当てはめます。この関数は、新しい単純モデルを含む lime オブジェクト newresults を返します。

fit は、いつ lime オブジェクト results を作成するかを指定する、単純モデル オプションを使用します。このオプションは、関数 fit の名前と値のペアの引数を使用して変更できます。

newresults = fit(results,queryPoint,numImportantPredictors,Name,Value) では、1 つ以上の名前と値のペアの引数を使用して追加オプションを指定します。たとえば、'SimpleModelType','tree' を指定して、決定木モデルを当てはめることができます。

例

線形単純モデルを使用した予測の説明

回帰モデルの学習を行い、線形単純モデルを使用する lime オブジェクトを作成します。lime オブジェクトを作成するときに、クエリ点と重要な予測子の数を指定しなかった場合、ソフトウェアは合成データ セットの標本を生成しますが、単純モデルの当てはめは行いません。オブジェクト関数 fit を使用して、クエリ点に単純モデルを当てはめます。次に、オブジェクト関数 plot を使用して、当てはめた線形単純モデルの係数を表示します。

carbig データ セットを読み込みます。このデータ セットには、1970 年代と 1980 年代初期に製造された自動車の測定値が格納されています。

load carbig

Acceleration、Cylinders などの予測子変数と応答変数 MPG が格納された table を作成します。

tbl = table(Acceleration,Cylinders,Displacement,Horsepower,Model_Year,Weight,MPG);

学習セットの欠損値を削除すると、メモリ消費量を減らして関数 fitrkernel の学習速度を向上させることができます。tbl の欠損値を削除します。

tbl = rmmissing(tbl);

tbl から応答変数を削除して、予測子変数のテーブルを作成します。

tblX = removevars(tbl,'MPG');

関数fitrkernelを使用して MPG の blackbox モデルの学習を行います。

rng('default') % For reproducibility
mdl = fitrkernel(tblX,tbl.MPG,'CategoricalPredictors',[2 5]);

lime オブジェクトを作成します。mdl には予測子データが含まれないため、予測子データ セットを指定します。

results = lime(mdl,tblX)

results = 
  lime with properties:

             BlackboxModel: [1x1 RegressionKernel]
              DataLocality: 'global'
     CategoricalPredictors: [2 5]
                      Type: 'regression'
                         X: [392x6 table]
                QueryPoint: []
    NumImportantPredictors: []
          NumSyntheticData: 5000
             SyntheticData: [5000x6 table]
                    Fitted: [5000x1 double]
               SimpleModel: []
       ImportantPredictors: []
            BlackboxFitted: []
         SimpleModelFitted: []

results には、生成された合成データ セットが含まれます。SimpleModel プロパティは空 ([]) です。

tblX の最初の観測値に線形単純モデルを当てはめます。検出する重要な予測子の数を 3 に指定します。

queryPoint = tblX(1,:)

queryPoint=1×6 table
    Acceleration    Cylinders    Displacement    Horsepower    Model_Year    Weight
    ____________    _________    ____________    __________    __________    ______

         12             8            307            130            70         3504 

results = fit(results,queryPoint,3);

オブジェクト関数 plot を使用して、lime オブジェクト results をプロットします。

plot(results)

プロットには、クエリ点についての 2 つの予測値が示されています。この予測値は、results のBlackboxFittedプロパティとSimpleModelFittedプロパティに対応します。

横棒グラフは、絶対値で並べ替えられた、単純モデルの係数値を示します。LIME は、クエリ点の重要な予測子として、Horsepower、Model_Year、および Cylinders を見つけます。

Model_Year および Cylinders は複数のカテゴリをもつカテゴリカル予測子です。線形単純モデルの場合、各カテゴリカル予測子について、カテゴリの数よりも 1 つ少ないダミー変数が作成されます。棒グラフには最も重要なダミー変数のみが表示されます。他のダミー変数の係数は results の SimpleModel プロパティを使用して確認できます。すべてのカテゴリカル ダミー変数を含む並べ替えられた係数の値を表示します。

[~,I] = sort(abs(results.SimpleModel.Beta),'descend');
table(results.SimpleModel.ExpandedPredictorNames(I)',results.SimpleModel.Beta(I), ...
    'VariableNames',{'Expanded Predictor Name','Coefficient'})

ans=17×2 table
     Expanded Predictor Name      Coefficient
    __________________________    ___________

    {'Horsepower'            }    -3.5035e-05
    {'Model_Year (74 vs. 70)'}    -6.1591e-07
    {'Model_Year (80 vs. 70)'}    -3.9803e-07
    {'Model_Year (81 vs. 70)'}     3.4186e-07
    {'Model_Year (82 vs. 70)'}    -2.2331e-07
    {'Cylinders (6 vs. 8)'   }    -1.9807e-07
    {'Model_Year (76 vs. 70)'}      1.816e-07
    {'Cylinders (5 vs. 8)'   }     1.7318e-07
    {'Model_Year (71 vs. 70)'}     1.5694e-07
    {'Model_Year (75 vs. 70)'}     1.5486e-07
    {'Model_Year (77 vs. 70)'}     1.5151e-07
    {'Model_Year (78 vs. 70)'}     1.3864e-07
    {'Model_Year (72 vs. 70)'}     6.8949e-08
    {'Cylinders (4 vs. 8)'   }     6.3098e-08
    {'Model_Year (73 vs. 70)'}     4.9696e-08
    {'Model_Year (79 vs. 70)'}    -2.4822e-08
      ⋮

複数のクエリ点に対する単純モデルの当てはめ

分類モデルの学習を行い、単純な決定木モデルを使用する lime オブジェクトを作成します。複数のクエリ点に複数のモデルを当てはめます。

CreditRating_Historical データ セットを読み込みます。データ セットには、顧客 ID、顧客の財務比率、業種ラベル、および信用格付けが格納されています。

tbl = readtable('CreditRating_Historical.dat');

tbl から顧客 ID と信用格付けの列を削除して、予測子変数の table を作成します。

tblX = removevars(tbl,["ID","Rating"]);

関数fitcecocを使用して、信用格付けの blackbox モデルに学習させます。

blackbox = fitcecoc(tblX,tbl.Rating,'CategoricalPredictors','Industry')

blackbox = 
  ClassificationECOC
           PredictorNames: {'WC_TA'  'RE_TA'  'EBIT_TA'  'MVE_BVTD'  'S_TA'  'Industry'}
             ResponseName: 'Y'
    CategoricalPredictors: 6
               ClassNames: {'A'  'AA'  'AAA'  'B'  'BB'  'BBB'  'CCC'}
           ScoreTransform: 'none'
           BinaryLearners: {21x1 cell}
               CodingName: 'onevsone'

blackbox モデルを使用して、lime オブジェクトを作成します。

rng('default') % For reproducibility
results = lime(blackbox);

真の信用格付け値がそれぞれ AAA および B となる 2 つのクエリ点を見つけます。

queryPoint(1,:) = tblX(find(strcmp(tbl.Rating,'AAA'),1),:);
queryPoint(2,:) = tblX(find(strcmp(tbl.Rating,'B'),1),:)

queryPoint=2×6 table
    WC_TA    RE_TA    EBIT_TA    MVE_BVTD    S_TA     Industry
    _____    _____    _______    ________    _____    ________

    0.121    0.413     0.057      3.647      0.466       12   
    0.019    0.009     0.042      0.257      0.119        1   

最初のクエリ点に線形単純モデルを当てはめます。重要な予測子の数を 4 に設定します。

newresults1 = fit(results,queryPoint(1,:),4);

最初のクエリ点についての LIME の結果 newresults1 をプロットします。

plot(newresults1)

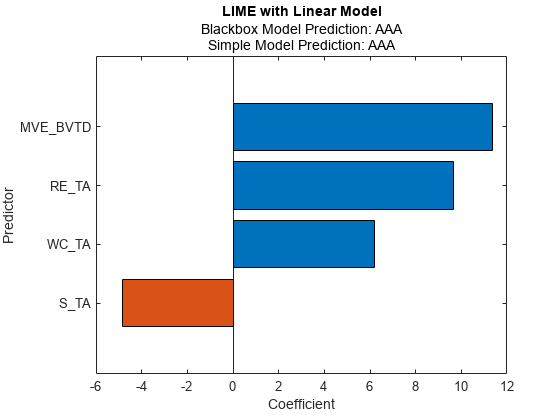
最初のクエリ点に線形決定木モデルを当てはめます。

newresults2 = fit(results,queryPoint(1,:),6,'SimpleModelType','tree');
plot(newresults2)

newresults1 および newresults2 の単純モデルはどちらも、重要な予測子として MVE_BVTD および RE_TA を見つけます。

2 番目のクエリ点に線形単純モデルを当てはめ、2 番目のクエリ点についての LIME の結果をプロットします。

newresults3 = fit(results,queryPoint(2,:),4);
plot(newresults3)

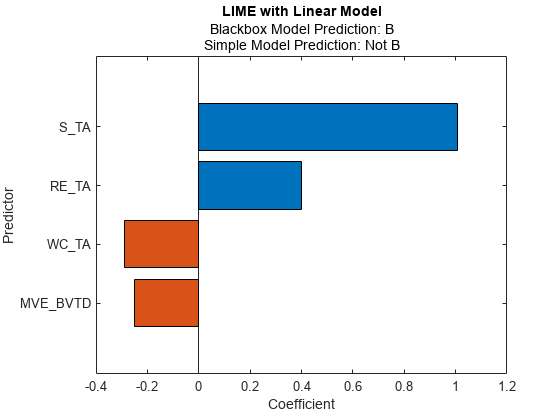
blackbox モデルからの予測値は B ですが、単純モデルからの予測値は B ではありません。2 つの予測値が同じでなければ、小さい方の 'KernelWidth' 値を指定することができます。ソフトウェアは、クエリ点に近い標本に比重を置く重みを使用して、単純モデルを当てはめます。クエリ点が外れ値であるか、判定境界の近くに位置する場合、小さい 'KernelWidth' 値を指定したとしても、2 つの予測値は異なる可能性があります。そのような場合、他の名前と値のペアの引数を変更することができます。たとえば、クエリ点についてのローカルな合成データ セットを生成 (lime の 'DataLocality' を 'local' として指定) し、合成データ セット内の標本数 (lime または fit の 'NumSyntheticData') を増やすことができます。異なる距離計量 (lime または fit の 'Distance') を使用することもできます。

小さな 'KernelWidth' 値で線形単純モデルを当てはめます。

newresults4 = fit(results,queryPoint(2,:),4,'KernelWidth',0.01);
plot(newresults4)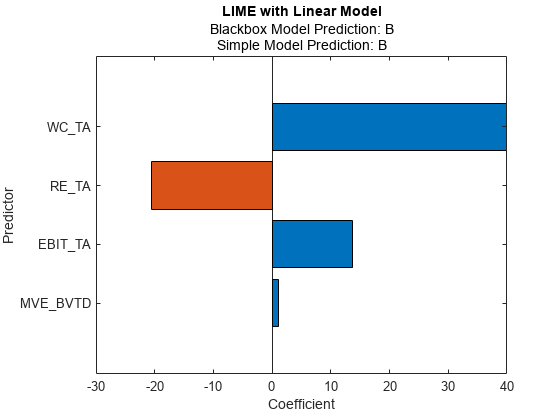

最初のクエリ点と 2 番目のクエリ点の格付けは、それぞれ AAA と B です。newresults1 および newresults4 の単純モデルはどちらも、重要な予測子として MVE_BVTD、RE_TA、および WC_TA を見つけます。ただし、これらの係数値は異なります。プロットは、これらの予測子が信用格付けに応じて異なる動作をすることを示しています。

入力引数

results — LIME の結果

lime オブジェクト

LIME の結果。lime オブジェクトとして指定します。

queryPoint — クエリ点

数値の行ベクトル | 単一行テーブル

関数 fit が単純モデルを当てはめる周囲のクエリ点。数値の行ベクトルまたは単一行テーブルとして指定します。queryPoint 値は、lime オブジェクト results 内の予測子データ (results.X または results.SyntheticData) とデータ型および列数が同じでなければなりません。

queryPoint に欠損値が含まれていてはなりません。

データ型: single | double | table

numImportantPredictors — 単純モデルで使用する重要な予測子の数

正の整数スカラー値

単純モデルで使用する重要な予測子の数。正の整数スカラー値として指定します。

• 'SimpleModelType' が 'linear' である場合、ソフトウェアは、指定された数の重要な予測子を選択し、選択した予測子の線形モデルを当てはめます。重要でない予測子は線形モデルの当てはめに使用されないことに注意してください。

• 'SimpleModelType' が 'tree' である場合、ソフトウェアは、重要な予測子の数として決定分岐 (枝ノード) の最大数を指定し、当てはめられた決定木が、指定された数を上限に予測子を使用するようにします。

numImportantPredictors 引数の既定値は、lime オブジェクト results の NumImportantPredictors プロパティ値です。results の作成時にこのプロパティ値を指定しない場合、プロパティ値は空 ([]) となるため、この引数を指定しなければなりません。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'NumSyntheticData',2000,'SimpleModelType','tree' は、合成データ セットのために生成する標本数を 2000 に設定し、単純モデルのタイプを決定木として指定します。

BetaTolerance — 線形単純モデルの線形係数とバイアス項の相対許容誤差

1e-4 (既定値) | 非負のスカラー

R2023b 以降

線形単純モデルの線形係数とバイアス項 (切片) の相対許容誤差。非負のスカラーとして指定します。

この引数は、SimpleModelType の値が "linear" の場合のみ有効です。

$$B_t=\left[{\beta }_t{}^{\prime }{b}_t\right]$$ であるとします。これは、当てはめのステップ t における係数とバイアス項のベクトルです。$${\Vert \frac{B_t-B_{t-1}}{B_t}\Vert }_2<\text{BetaTolerance}$$ で線形単純モデルの当てはめプロセスが終了します。

例: "BetaTolerance",1e-8

データ型: single | double

Cov — マハラノビス距離計量の共分散行列

正定値行列

マハラノビス距離計量の共分散行列。'Cov' と K 行 K 列の正定値行列で構成されるコンマ区切りのペアとして指定します。K は予測子の数です。

この引数は、'Distance' が 'mahalanobis' である場合のみ有効です。

既定値は、lime オブジェクト results を作成する際に指定する 'Cov' 値です。lime の既定の 'Cov' 値は cov(PD,'omitrows') です。ここで、PD は予測子データ、または合成予測子データです。'Cov' 値を指定しなかった場合、ソフトウェアは、予測子データおよび合成予測子データの両方の距離を計算するときに、異なる共分散行列を使用します。

例: 'Cov',eye(3)

データ型: single | double

Distance — 距離計量

文字ベクトル | string スカラー | 関数ハンドル

距離計量。'Distance' と文字ベクトル、string スカラー、または関数ハンドルで構成されるコンマ区切りのペアとして指定します。

• 予測子データに連続変数のみが含まれる場合、fit はこれらの距離計量をサポートします。

  値	説明
  'euclidean'	ユークリッド距離。
  'seuclidean'	標準化されたユークリッド距離。観測値間の各座標差は、標準偏差 S = std(PD,'omitnan') の対応する要素で除算することによりスケーリングされます。ここで、PD は予測子データ、または合成予測子データです。別のスケーリングを指定するには、名前と値の引数 'Scale' を使用します。
  'mahalanobis'	PD の標本共分散を使用したマハラノビス距離、C = cov(PD,'omitrows')。共分散行列の値を変更するには、名前と値の引数 'Cov' を使用します。
  'cityblock'	市街地距離。
  'minkowski'	ミンコフスキー距離。既定の指数は 2 です。別の指数を指定するには、名前と値の引数 'P' を使用します。
  'chebychev'	チェビシェフ距離 (最大座標差)。
  'cosine'	1 から、ベクトルとして扱われる点の間の夾角の余弦を引いた値。
  'correlation'	1 から、値の系列として扱われる点の間の標本相関を引いた値。
  'spearman'	1 から、観測値間の標本スピアマンの順位相関 (値の系列として扱われる) を引いた値。
  @distfun	カスタム距離関数のハンドル。距離関数の形式は次のようになります。 function D2 = distfun(ZI,ZJ) % calculation of distance ... ここで ZI は、単一の観測値が含まれている 1 行 t 列のベクトルです。 ZJ は、複数の観測値が含まれている s 行 t 列の行列です。distfun は、任意の個数の観測値が含まれている行列 ZJ を受け入れなければなりません。 D2 は s 行 1 列の距離のベクトルであり、D2(k) は観測値 ZI と ZJ(k,:) の間の距離です。 データがスパースでない場合、通常は関数ハンドルではなく組み込みの距離計量を使用する方が高速に距離を計算できます。

• 予測子データに連続変数とカテゴリカル変数の両方が含まれる場合、fit はこれらの距離計量をサポートします。

  値	説明
  'goodall3'	異形グドール距離
  'ofd'	出現頻度距離

定義については距離計量を参照してください。

既定値は、lime オブジェクト results を作成する際に指定する 'Distance' 値です。lime の既定の 'Distance' 値は、予測子データに連続変数のみが含まれる場合は 'euclidean'、予測子データに連続変数とカテゴリカル変数の両方が含まれている場合は 'goodall3' です。

例: 'Distance','ofd'

データ型: char | string | function_handle

KernelWidth — カーネルの幅

数値スカラー値

二乗指数 (またはガウス) カーネル関数のカーネルの幅。'KernelWidth' と数値スカラー値で構成されるコンマ区切りのペアとして指定します。

関数 fit は、クエリ点と合成予測子データ セット内の標本の間の距離を計算し、その距離を二乗指数カーネル関数を使用して重みに変換します。'KernelWidth' 値を低くすると、fit が使用する重みは、クエリ点に近い標本に重点を置くものになります。詳細については、LIMEを参照してください。

既定値は、lime オブジェクト results を作成する際に指定する 'KernelWidth' 値です。lime の既定の 'KernelWidth' 値は 0.75 です。

例: 'KernelWidth',0.5

データ型: single | double

NumNeighbors — クエリ点の近傍の数

正の整数スカラー値

クエリ点の近傍の数。'NumNeighbors' と正の整数スカラー値で構成されるコンマ区切りのペアとして指定します。この引数は、results の DataLocality プロパティが 'local' である場合のみ有効です。

関数 fit は、指定されたクエリ点の最近傍の数を使用して、予測子データの分布パラメーターを推定します。その後、推定した分布を使用して、合成予測子データを生成します。

lime オブジェクト results 内の予測子データ セット (results.X) における観測値の数より大きい値が指定された場合、fit はすべての観測値を使用します。

既定値は、lime オブジェクト results を作成する際に指定する 'NumNeighbors' 値です。lime の既定の 'NumNeighbors' 値は 1500 です。

例: 'NumNeighbors',2000

データ型: single | double

NumSyntheticData — 合成データ セットのために生成する標本の数

results.NumSyntheticData (既定値) | 正の整数スカラー値

合成データ セットのために生成する標本の数。'NumSyntheticData' と正の整数スカラー値で構成されるコンマ区切りのペアとして指定します。

既定値は、lime オブジェクト results の NumSyntheticData プロパティ値です。results の作成時にカスタム合成データ セットを指定した場合、このプロパティ値はそのデータ セットの標本数です。それ以外の場合は、results を作成する際に指定する 'NumSyntheticData' 値によってこのプロパティが設定されます。lime の既定の 'NumSyntheticData' 値は 5000 です。

例: 'NumSyntheticData',2500

データ型: single | double

P — ミンコフスキー距離計量の指数

正のスカラー

ミンコフスキー距離計量の指数。'P' と正のスカラー値をコンマで区切って指定します。

この引数は、'Distance' が 'minkowski' である場合のみ有効です。

既定値は、lime オブジェクト results を作成する際に指定する 'P' 値です。lime の既定の 'P' 値は 2 です。

例: 'P',3

データ型: single | double

Scale — 標準化されたユークリッド距離計量のスケール パラメーター値

非負の数値ベクトル

標準化されたユークリッド距離計量のスケール パラメーター値。'Scale' と長さ K の非負の数値ベクトルで構成されるコンマ区切りのペアとして指定します。K は予測子の数です。

この引数は、'Distance' が 'seuclidean' である場合のみ有効です。

既定値は、lime オブジェクト results を作成する際に指定する 'Scale' 値です。lime の既定の 'Scale' 値は std(PD,'omitnan') です。ここで、PD は予測子データ、または合成予測子データです。'Scale' 値を指定しなかった場合、ソフトウェアは、予測子データおよび合成予測子データの両方の距離を計算するときに、異なるスケール パラメーターを使用します。

例: 'Scale',quantile(X,0.75) - quantile(X,0.25)

データ型: single | double

SimpleModelType — 単純モデルのタイプ

'linear' | 'tree'

単純モデルのタイプ。'SimpleModelType' と 'linear' または 'tree' で構成されるコンマ区切りのペアとして指定します。

• 'linear' — ソフトウェアは、回帰には fitrlinear を、分類には fitclinear を使用して、線形モデルを当てはめます。

• 'tree' — ソフトウェアは、回帰には fitrtree を、分類には fitctree を使用して、決定木モデルを当てはめます。

既定値は、lime オブジェクト results を作成する際に指定する 'SimpleModelType' 値です。lime の既定の 'SimpleModelType' 値は 'linear' です。

例: 'SimpleModelType','tree'

データ型: char | string

出力引数

newresults — LIME の結果

lime オブジェクト

LIME の結果。lime オブジェクトとして返されます。newresults に新しい単純モデルが格納されます。

入力引数 results を上書きするには、fit の出力を results に代入します。

results = fit(results,queryPoint,numImportantPredictors);

詳細

距離計量

距離計量は、2 つの観測値の間の距離を定義する関数です。fit は、連続変数用のさまざまな距離計量や、連続変数とカテゴリカル変数の混在をサポートします。

• 連続変数の距離計量

  mx 行 n 列のデータ行列 X (mx 個の 1 行 n 列の行ベクトル x₁、x₂、...、x_mx として扱われる) と、my 行 n 列のデータ行列 Y (my 個の 1 行 n 列の行ベクトル y₁、y₂、...、y_my として扱われる) が与えられた場合、ベクトル x_s と y_t の間のさまざまな距離は次のように定義されます。

  • ユークリッド距離

    $$d_{st}^2=(x_s-y_t)(x_s-y_t{)}^{\prime }.$$

    ユークリッド距離はミンコフスキー距離の特殊なケース、p = 2 の場合です。

    ユークリッド距離を指定するには、Distance パラメーターを 'euclidean' に設定します。

  • 標準化されたユークリッド距離

    $$d_{st}^2=(x_s-y_t)V^{-1}(x_s-y_t{)}^{\prime },$$

    ここで、V は j 番目の対角要素が (S(j))² である n 行 n 列の対角行列です。S は各次元のスケーリング係数のベクトルです。

    標準化されたユークリッド距離を指定するには、Distance パラメーターを 'seuclidean' に設定します。

  • マハラノビス距離

    $$d_{st}^2=(x_s-y_t)C^{-1}(x_s-y_t{)}^{\prime },$$

    ここで、C は共分散行列です。

    マハラノビス距離を指定するには、Distance パラメーターを 'mahalanobis' に設定します。

  • 市街地距離

    $$d_{st}={\displaystyle \sum _{j=1}^n\left|x_{sj}-y_{tj}\right|}.$$

    市街地距離はミンコフスキー距離の特殊なケース、p = 1 の場合です。

    市街地距離を指定するには、Distance パラメーターを 'cityblock' に設定します。

  • ミンコフスキー距離

    $$d_{st}=\sqrt[p]{{\displaystyle \sum _{j=1}^n{\left|x_{sj}-y_{tj}\right|}^p}}.$$

    p = 1 という特殊なケースでは、ミンコフスキー距離は市街地距離を与えます。p = 2 という特殊なケースでは、ミンコフスキー距離はユークリッド距離を与えます。p = ∞ という特殊なケースでは、ミンコフスキー距離はチェビシェフ距離を与えます。

    ミンコフスキー距離を指定するには、Distance パラメーターを 'minkowski' に設定します。

  • チェビシェフ距離

    $$d_{st}={\max }_j\left\{\left|x_{sj}-y_{tj}\right|\right\}.$$

    チェビシェフ距離はミンコフスキー距離の特殊なケース、p = ∞ の場合です。

    チェビシェフ距離を指定するには、Distance パラメーターを 'chebychev' に設定します。

  • コサイン距離

    $$d_{st}=\left(1-\frac{x_s{y^{\prime }}_t}{\sqrt{\left(x_s{x^{\prime }}_s\right)\left(y_t{y^{\prime }}_t\right)}}\right).$$

    コサイン距離を指定するには、Distance パラメーターを 'cosine' に設定します。

  • 相関距離

    $$d_{st}=1-\frac{\left(x_s-{\overline{x}}_s\right){\left(y_t-{\overline{y}}_t\right)}^{\prime }}{\sqrt{\left(x_s-{\overline{x}}_s\right){\left(x_s-{\overline{x}}_s\right)}^{\prime }}\sqrt{\left(y_t-{\overline{y}}_t\right){\left(y_t-{\overline{y}}_t\right)}^{\prime }}},$$

    ここで

    $${\overline{x}}_s=\frac{1}{n}{\displaystyle \sum _j{x}_{sj}}$$

    および

    $${\overline{y}}_t=\frac{1}{n}{\displaystyle \sum _j{y}_{tj}}.$$

    相関距離を指定するには、Distance パラメーターを 'correlation' に設定します。

  • スピアマン距離は、1 から一連の値として扱われる観測値間の標本スピアマン順位相関係数を引きます。

    $$d_{st}=1-\frac{\left(r_s-{\overline{r}}_s\right){\left(r_t-{\overline{r}}_t\right)}^{\prime }}{\sqrt{\left(r_s-{\overline{r}}_s\right){\left(r_s-{\overline{r}}_s\right)}^{\prime }}\sqrt{\left(r_t-{\overline{r}}_t\right){\left(r_t-{\overline{r}}_t\right)}^{\prime }}},$$

    ここで

    • r_sj は、tiedrank により計算される、x_1j、x_2j、...x_mx,j から取得された x_sj の順位です。

    • r_tj は、tiedrank により計算される、y_1j、y_2j、...y_my,j から取得された y_tj の順位です。

    • r_s および r_t は、x_s および y_t の座標単位の順位ベクトルです。つまり、r_s = (r_s1, r_s2, ... r_sn) および r_t = (r_t1, r_t2, ... r_tn) です。

    • $${\overline{r}}_s=\frac{1}{n}{\displaystyle \sum _j{r}_{sj}}=\frac{\left(n+1\right)}{2}$$.

    • $${\overline{r}}_t=\frac{1}{n}{\displaystyle \sum _j{r}_{tj}}=\frac{\left(n+1\right)}{2}$$.

    スピアマン距離を指定するには、Distance パラメーターを 'spearman' に設定します。

• 連続変数とカテゴリカル変数が混在する場合の距離計量

  • 異形グドール距離

    この距離は、グドール距離のバリアントであり、他の値の頻度に関係なく、一致する値が互いに離れた場所にある場合に小さな距離を割り当てます。不一致の場合、予測子の距離寄与は 1/(変数の数) です。

    異形グドール距離を指定するには、Distance パラメーターを 'goodall3' に設定します。

  • 出現頻度距離

    一致の場合、出現頻度距離はゼロ距離を割り当てます。不一致の場合、出現頻度距離は、頻度の低い値に高い距離を割り当て、頻度の高い値に低い距離を割り当てます。

    出現頻度距離を指定するには、Distance パラメーターを 'ofd' に設定します。

アルゴリズム

LIME

手順 1 ～ 5 の記載のとおり、LIME [1]を使用して機械学習モデルの予測を説明するため、ソフトウェアは、合成データ セットを生成し、lime と fit を使用して解釈可能な単純モデルを合成データ セットに当てはめます。

• lime の queryPoint 値と numImportantPredictors 値を指定した場合、関数 lime はすべての手順を実行します。

• queryPoint および numImportantPredictors を指定せずに 'DataLocality' を 'global' (既定の設定) として指定した場合、関数 lime が合成データ セットを生成し (手順 1 ～ 2)、関数 fit が単純モデルを当てはめます (手順 3 ～ 5)。

• queryPoint および numImportantPredictors を指定せずに 'DataLocality' を 'local' として指定した場合、関数 fit はすべての手順を実行します。

関数 lime および fit は、以下の手順を実行します。

1. 連続変数には多変量正規分布を、各カテゴリカル変数には多変量分布を使用して、合成予測子データ セット X_s を生成します。名前と値の引数 'NumSyntheticData' を使用して、生成する標本の数を指定できます。

   • 'DataLocality' が 'global' (既定の設定) である場合、ソフトウェアは、予測子データ セット全体 (X または blackbox 内の予測子データ) から分布パラメーターを推定します。

   • 'DataLocality' が 'local' である場合、ソフトウェアは、クエリ点の k 個の最近傍を使用して分布パラメーターを推定します。ここで、k は 'NumNeighbors' 値です。名前と値の引数 'Distance' を使用して、最近傍を見つけるための距離計量を指定できます。

   ソフトウェアは、分布パラメーターを推定する際、予測子データ セット内の欠損値を無視します。

   あるいは、lime の入力引数 customSyntheticData を使用することで、事前生成されたカスタム合成予測子データ セットを提供できます。

2. 合成データ セット X_s についての予測値 Y_s を計算します。この予測値は、回帰、または分類を行うための分類済みラベルについての予測応答です。ソフトウェアは、blackbox モデルの関数 predict を使用して予測値を計算します。blackbox を関数ハンドルとして指定した場合、ソフトウェアは、その関数ハンドルを使用して予測値を計算します。

3. 'Distance' によって指定された距離計量を使用して、クエリ点と合成予測子データ セット内の標本の距離 d を計算します。

4. 二乗指数 (またはガウス) カーネル関数を使用して、クエリ点 q に対する合成予測子データ セット内の標本の重み値 w_q を計算します。

   $$w_q(x_s)=\exp \left(-\frac{1}{2}{\left(\frac{d(x_s,q)}{\sqrt{p}\sigma }\right)}^2\right).$$

   • x_s は、合成予測子データ セット X_s 内の標本です。

   • d(x_s,q) は、標本 x_s とクエリ点 q の距離です。

   • p は、X_s 内の予測子の数です。

   • σ はカーネルの幅です。名前と値の引数 'KernelWidth' を使用して指定できます。既定の 'KernelWidth' 値は 0.75 です。

   クエリ点における重み値は 1 であり、距離の値が大きくなるにつれ、0 に収束していきます。'KernelWidth' 値は、重み値が 0 に収束する速度を制御します。'KernelWidth' 値が小さければ、重み値はより速く 0 に収束します。その結果、アルゴリズムは、クエリ点に近い標本に、より大きな重みを付与します。このような重み値がアルゴリズムによって使用されることで、選択された重要な予測子、および当てはめられた単純モデルによる、クエリ点周辺の合成データについての予測子の局所的な説明が有効となります。

5. 単純モデルを当てはめます。

   • 'SimpleModelType' が 'linear' (既定の設定) である場合、ソフトウェアは、重要な予測子を選択し、選択した重要な予測子の線形モデルを当てはめます。

     • グループ直交マッチング追跡 (OMP) アルゴリズム[2][3]を使用して、n 個の重要な予測子 ($${\tilde{X}}_s$$) を選択します。ここで、n は numImportantPredictors 値です。このアルゴリズムは、合成予測子データ セット (X_s)、予測子 (Y_s)、および重み値 (w_q) を使用します。

       重要でない予測子 (推定される係数が 0 の予測子) は選択されないことに注意してください。したがって、選択される重要な予測子の数は n 未満になることがあります。

     • 重み値 (w_q) を使用して、選択した重要な予測子 ($${\tilde{X}}_s$$) の線形モデルを予測子 (Y_s) に当てはめます。ソフトウェアは、回帰には fitrlinear を、分類には fitclinear を使用します。マルチクラス モデルの場合、ソフトウェアは、1 対他 (OVA) 方式を使用してバイナリ分類問題を作成します。陽性クラスは blackbox モデルからのクエリ点についての予測クラスであり、陰性クラスはその他のクラスを指します。

   • 'SimpleModelType' が 'tree' である場合、ソフトウェアは、回帰には fitrtree を、分類には fitctree を使用して決定木モデルを当てはめます。ソフトウェアは、重要な予測子の数として決定分岐 (枝ノード) の最大数を指定し、当てはめられた決定木が、指定された数を上限に予測子を使用するようにします。

参照

[1] Ribeiro, Marco Tulio, S. Singh, and C. Guestrin. "'Why Should I Trust You?': Explaining the Predictions of Any Classifier." In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1135–44. San Francisco, California: ACM, 2016.

[2] Świrszcz, Grzegorz, Naoki Abe, and Aurélie C. Lozano. "Grouped Orthogonal Matching Pursuit for Variable Selection and Prediction." Advances in Neural Information Processing Systems (2009): 1150–58.

[3] Lozano, Aurélie C., Grzegorz Świrszcz, and Naoki Abe. "Group Orthogonal Matching Pursuit for Logistic Regression." Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (2011): 452–60.

バージョン履歴

R2020b で導入

R2023b: LIME で線形単純モデルの BetaTolerance の指定をサポート

線形単純モデル (SimpleModelType を参照) を当てはめて LIME の値を計算する場合に、名前と値の引数 BetaTolerance を使用して単純モデルの線形係数とバイアス項の相対許容誤差を指定できます。BetaTolerance の既定値は 1e-4 です。

R2023a では、線形単純モデルの線形係数の相対許容誤差は 1e-8 でした。以前のリリースでは、値は 1e-4 でした。

参考

lime | plot

トピック

• 機械学習モデルの解釈