fitrgp

ガウス過程回帰 (GPR) モデルの当てはめ

構文

gprMdl = fitrgp(Tbl,ResponseVarName)

gprMdl = fitrgp(Tbl,formula)

gprMdl = fitrgp(Tbl,y)

gprMdl = fitrgp(X,y)

gprMdl = fitrgp(___,Name,Value)

説明

gprMdl = fitrgp(Tbl,ResponseVarName) は、Tbl 内の標本データを使用して学習させたガウス過程回帰 (GPR) モデルを返します。ResponseVarName は、Tbl 内の応答変数の名前です。

gprMdl = fitrgp(Tbl,formula) は、formula で特定された予測子変数および応答変数について、Tbl 内の標本データを使用して学習させたガウス過程回帰 (GPR) モデルを返します。

gprMdl = fitrgp(Tbl,y) は、テーブル Tbl 内の応答変数および連続応答ベクトル y についての GPR モデルを返します。

gprMdl = fitrgp(X,y) は、予測子 X および連続応答ベクトル y についての GPR モデルを返します。

gprMdl = fitrgp(___,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して、前の構文の入力引数のいずれかについて GPR モデルを返します。

たとえば、近似法、予測法、共分散関数またはアクティブ セット選択法を指定できます。交差検証済みモデルを学習させることもできます。

gprMdl は、RegressionGP オブジェクトです。このオブジェクトのオブジェクト関数とプロパティについては、RegressionGP を参照してください。

交差検証済みモデルを学習させた場合、gprMdl は RegressionPartitionedGP オブジェクトになります。交差検証したオブジェクトをさらに分析するには、RegressionPartitionedGP オブジェクトのオブジェクト関数を使用します。

例

テーブル内のデータの使用による GPR モデルの学習

この例では、UCI Machine Learning Repository [3]にあるアワビのデータ[1]、[2]を使用します。データをダウンロードして、abalone.data という名前で現在のフォルダに保存します。

データをテーブルに格納します。最初の 7 行を表示します。

tbl = readtable('abalone.data','Filetype','text',...
     'ReadVariableNames',false);
tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height',...
     'WWeight','SWeight','VWeight','ShWeight','NoShellRings'};
tbl(1:7,:)

ans = 

    Sex    Length    Diameter    Height    WWeight    SWeight    VWeight    ShWeight    NoShellRings
    ___    ______    ________    ______    _______    _______    _______    ________    ____________

    'M'    0.455     0.365       0.095      0.514     0.2245      0.101      0.15       15          
    'M'     0.35     0.265        0.09     0.2255     0.0995     0.0485      0.07        7          
    'F'     0.53      0.42       0.135      0.677     0.2565     0.1415      0.21        9          
    'M'     0.44     0.365       0.125      0.516     0.2155      0.114     0.155       10          
    'I'     0.33     0.255        0.08      0.205     0.0895     0.0395     0.055        7          
    'I'    0.425       0.3       0.095     0.3515      0.141     0.0775      0.12        8          
    'F'     0.53     0.415        0.15     0.7775      0.237     0.1415      0.33       20

このデータセットには、4177 個の観測値が含まれています。目標は、8 つの物理的な測定値からアワビの年齢を予測することです。最後の変数は貝殻の輪の数で、アワビの年齢を示します。最初の予測子は、カテゴリカル変数です。テーブルの最後の変数は、応答変数です。

パラメーター推定に回帰変数サブセット法を、予測に完全独立条件法を使用して、GPR モデルを当てはめます。予測子を標準化します。

gprMdl = fitrgp(tbl,'NoShellRings','KernelFunction','ardsquaredexponential',...
      'FitMethod','sr','PredictMethod','fic','Standardize',1)

grMdl = 

  RegressionGP
       PredictorNames: {1x8 cell}
         ResponseName: 'Var9'
    ResponseTransform: 'none'
      NumObservations: 4177
       KernelFunction: 'ARDSquaredExponential'
    KernelInformation: [1x1 struct]
        BasisFunction: 'Constant'
                 Beta: 10.9148
                Sigma: 2.0243
    PredictorLocation: [10x1 double]
       PredictorScale: [10x1 double]
                Alpha: [1000x1 double]
     ActiveSetVectors: [1000x10 double]
        PredictMethod: 'FIC'
        ActiveSetSize: 1000
            FitMethod: 'SR'
      ActiveSetMethod: 'Random'
    IsActiveSetVector: [4177x1 logical]
        LogLikelihood: -9.0013e+03
     ActiveSetHistory: [1x1 struct]
       BCDInformation: []

学習済みのモデルを使用して、応答を予測します。

ypred = resubPredict(gprMdl);

真の応答と予測応答をプロットします。

figure();
plot(tbl.NoShellRings,'r.');
hold on
plot(ypred,'b');
xlabel('x');
ylabel('y');
legend({'data','predictions'},'Location','Best');
axis([0 4300 0 30]);
hold off;

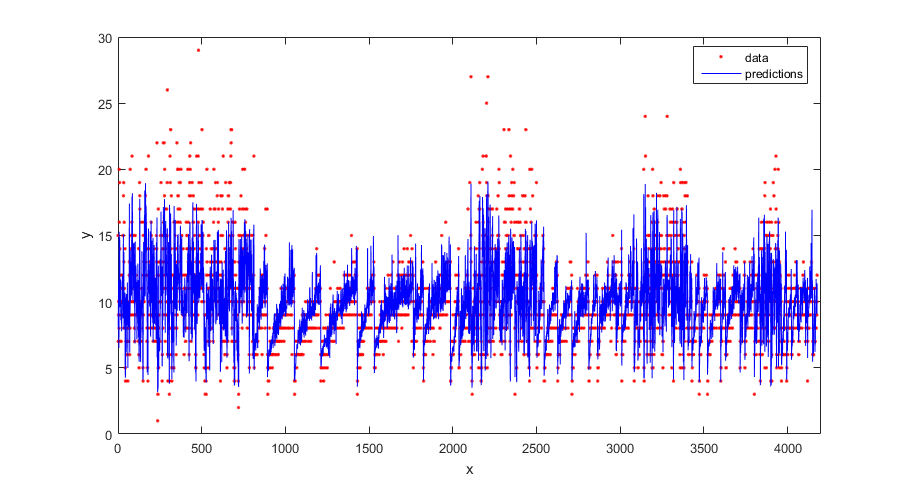
学習済みのモデルについて学習データの回帰損失 (再代入損失) を計算します。

L = resubLoss(gprMdl)

L =

    4.0064

GPR モデルの学習と予測のプロット

標本データを生成します。

rng(0,'twister'); % For reproducibility
n = 1000;
x = linspace(-10,10,n)';
y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);

パラメーターの推定に線形基底関数と厳密近似法を使用して、GPR モデルを当てはめます。厳密予測法も使用します。

gprMdl = fitrgp(x,y,'Basis','linear',...
      'FitMethod','exact','PredictMethod','exact');

学習済みのモデルを使用して、x の行に対応する応答を予測します (再代入予測)。

ypred = resubPredict(gprMdl);

真の応答と予測値をプロットします。

plot(x,y,'b.');
hold on;
plot(x,ypred,'r','LineWidth',1.5);
xlabel('x');
ylabel('y');
legend('Data','GPR predictions');
hold off

初期カーネル パラメーター値の指定による影響

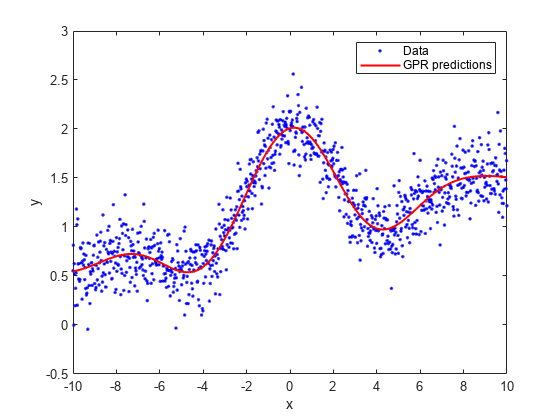
標本データを読み込みます。

load('gprdata2.mat')

このデータには、1 つの予測子変数と連続応答が含まれています。このデータは、シミュレーションされたものです。

既定のカーネル パラメーターで二乗指数カーネル関数を使用して、GPR モデルを当てはめます。

gprMdl1 = fitrgp(x,y,'KernelFunction','squaredexponential');

次に、2 番目のモデルを当てはめます。今回は、カーネル パラメーターの初期値を指定します。

sigma0 = 0.2;
kparams0 = [3.5, 6.2];
gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential',...
     'KernelParameters',kparams0,'Sigma',sigma0);

両方のモデルから再代入予測を計算します。

ypred1 = resubPredict(gprMdl1);
ypred2 = resubPredict(gprMdl2);

両方のモデルの応答予測と学習データの応答をプロットします。

figure();
plot(x,y,'r.');
hold on
plot(x,ypred1,'b');
plot(x,ypred2,'g');
xlabel('x');
ylabel('y');
legend({'data','default kernel parameters',...
'kparams0 = [3.5,6.2], sigma0 = 0.2'},...
'Location','Best');
title('Impact of initial kernel parameter values');
hold off

GPR パラメーターを推定するために fitrgp が最大化する周辺の対数尤度には、複数のローカルな解が存在します。どの解に収束するかは、初期点によって決まります。それぞれのローカルな解は、特定のデータ解釈に対応します。この例では、既定の初期カーネル パラメーターを使用した解は、ノイズが多い低周波信号に対応します。一方、カスタムな初期カーネル パラメーターを使用した 2 番目の解は、ノイズが少ない高周波信号に対応します。

予測子ごとに異なる長さスケールの使用

標本データを読み込みます。

load('gprdata.mat')

6 つの連続予測子変数があります。学習データ セットには 500 個の観測値が、テスト データ セットには 100 個の観測値があります。このデータは、シミュレーションされたものです。

各予測子について長さスケールが異なる二乗指数カーネル関数を使用して、GPR モデルを当てはめます。この共分散関数は、次のように定義されます。

$$k(x_i,x_j|\theta )={\sigma }_f^{2}exp\left[-\frac{1}{2}\sum _{m=1}^d\frac{{(x_{im}-x_{jm})}^2}{{\sigma }_m^2}\right].$$

ここで、$${\sigma }_m$$ は予測子 $$m$$ ($$m$$ = 1、2、...、) の長さスケールを表します。$$d$$ と $${\sigma }_f$$ は信号標準偏差です。制約がないパラメーター化 $$\theta$$ は、次のようになります。

$$\begin{array}{l}{\theta }_m=\log {\sigma }_m,form=1,2,...,d\\ {\theta }_{d+1}=\log {\sigma }_f.\end{array}$$

カーネル関数の長さスケールを 10 で、信号標準偏差とノイズ標準偏差を応答の標準偏差で初期化します。

sigma0 = std(ytrain);
sigmaF0 = sigma0;
d = size(Xtrain,2);
sigmaM0 = 10*ones(d,1);

カーネル パラメーターの初期値を使用して、GPR モデルを当てはめます。学習データの予測子を標準化します。厳密な近似法および予測法を使用します。

gprMdl = fitrgp(Xtrain,ytrain,'Basis','constant','FitMethod','exact',...
'PredictMethod','exact','KernelFunction','ardsquaredexponential',...
'KernelParameters',[sigmaM0;sigmaF0],'Sigma',sigma0,'Standardize',1);

テスト データの回帰損失を計算します。

L = loss(gprMdl,Xtest,ytest)

L = 0.6919

カーネル情報にアクセスします。

gprMdl.KernelInformation

ans = struct with fields:
                    Name: 'ARDSquaredExponential'
        KernelParameters: [7x1 double]
    KernelParameterNames: {7x1 cell}

カーネル パラメーターの名前を表示します。

gprMdl.KernelInformation.KernelParameterNames

ans = 7x1 cell
    {'LengthScale1'}
    {'LengthScale2'}
    {'LengthScale3'}
    {'LengthScale4'}
    {'LengthScale5'}
    {'LengthScale6'}
    {'SigmaF'      }

カーネル パラメーターを表示します。

sigmaM = gprMdl.KernelInformation.KernelParameters(1:end-1,1)

sigmaM = 6×1
104 ×

    0.0004
    0.0007
    0.0004
    4.7637
    0.1018
    0.0056

sigmaF = gprMdl.KernelInformation.KernelParameters(end)

sigmaF = 28.1720

sigma  = gprMdl.Sigma

sigma = 0.8162

学習した長さスケールの対数をプロットします。

figure()
plot((1:d)',log(sigmaM),'ro-');
xlabel('Length scale number');
ylabel('Log of length scale');

4 番目と 5 番目の予測子変数における長さスケールの対数が、他と比較して大きくなっています。これらの予測子変数は、他の予測子変数ほどは応答に影響を与えないようです。

4 番目と 5 番目の変数を予測子変数として使用せずに GPR モデルを当てはめます。

X = [Xtrain(:,1:3) Xtrain(:,6)];
sigma0 = std(ytrain);
sigmaF0 = sigma0;
d = size(X,2);
sigmaM0 = 10*ones(d,1);

gprMdl = fitrgp(X,ytrain,'Basis','constant','FitMethod','exact',...
'PredictMethod','exact','KernelFunction','ardsquaredexponential',...
'KernelParameters',[sigmaM0;sigmaF0],'Sigma',sigma0,'Standardize',1);

テスト データの回帰誤差を計算します。

xtest = [Xtest(:,1:3) Xtest(:,6)];
L = loss(gprMdl,xtest,ytest)

L = 0.6928

損失は、すべての変数を予測子変数として使用した場合と同じような値になっています。

テスト データについて予測応答を計算します。

 ypred = predict(gprMdl,xtest);

元の応答および当てはめた値をプロットします。

figure;
plot(ytest,'r');
hold on;
plot(ypred,'b');
legend('True response','GPR predicted values','Location','Best');
hold off

GPR 回帰の最適化

この例では、fitrgp を使用して自動的にハイパーパラメーターを最適化する方法を示します。この例では、ソフトウェアに含まれている gprdata2 データを使用します。

データを読み込みます。

load('gprdata2.mat')

このデータには、1 つの予測子変数と連続応答が含まれています。このデータは、シミュレーションされたものです。

既定のカーネル パラメーターで二乗指数カーネル関数を使用して、GPR モデルを当てはめます。

gprMdl1 = fitrgp(x,y,'KernelFunction','squaredexponential');

自動的なハイパーパラメーター最適化を使用して、5 分割交差検証損失を最小化するハイパーパラメーターを求めます。

再現性を得るために、乱数シードを設定し、'expected-improvement-plus' の獲得関数を使用します。

rng default
gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential',...
    'OptimizeHyperparameters','auto','HyperparameterOptimizationOptions',...
    struct('AcquisitionFunctionName','expected-improvement-plus'));

|=====================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |        Sigma |  Standardize |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |     0.42258 |      1.7379 |     0.42258 |     0.42258 |       2.7255 |        false |
|    2 | Best   |     0.29417 |       2.173 |     0.29417 |      0.3301 |    0.0057724 |         true |
|    3 | Accept |      1.6498 |       1.316 |     0.29417 |      0.3383 |       25.905 |         true |
|    4 | Best   |     0.29417 |      2.6237 |     0.29417 |     0.29425 |    0.0098001 |        false |
|    5 | Best   |    0.039309 |       2.406 |    0.039309 |    0.039451 |       0.1084 |        false |
|    6 | Accept |     0.29417 |      2.9699 |    0.039309 |    0.039469 |   0.00010031 |         true |
|    7 | Accept |     0.29417 |      2.5094 |    0.039309 |     0.15983 |   0.00010039 |        false |
|    8 | Accept |    0.039845 |      2.4033 |    0.039309 |    0.038857 |     0.095793 |        false |
|    9 | Best   |    0.037789 |       2.325 |    0.037789 |      0.0374 |      0.17968 |        false |
|   10 | Accept |     0.29417 |      2.8881 |    0.037789 |    0.037408 |   0.00079688 |         true |
|   11 | Accept |    0.037908 |      2.2021 |    0.037789 |    0.035598 |      0.13877 |        false |
|   12 | Accept |    0.037911 |      2.9842 |    0.037789 |    0.036245 |      0.13814 |        false |
|   13 | Accept |    0.037915 |      3.0129 |    0.037789 |    0.036619 |      0.13705 |        false |
|   14 | Best   |    0.037728 |      2.4258 |    0.037728 |    0.037263 |      0.35683 |         true |
|   15 | Accept |    0.039463 |      2.2343 |    0.037728 |    0.037144 |      0.10174 |         true |
|   16 | Accept |    0.037752 |      2.6095 |    0.037728 |    0.037322 |      0.19898 |         true |
|   17 | Accept |      0.2865 |      2.7158 |    0.037728 |    0.037801 |     0.046127 |         true |
|   18 | Accept |     0.29417 |      3.7153 |    0.037728 |    0.037799 |   0.00078483 |        false |
|   19 | Accept |      2.0992 |      2.2966 |    0.037728 |    0.037943 |         29.2 |        false |
|   20 | Accept |     0.42266 |      1.6255 |    0.037728 |     0.03731 |      0.65474 |        false |
|=====================================================================================================|
| Iter | Eval   | Objective:  | Objective   | BestSoFar   | BestSoFar   |        Sigma |  Standardize |
|      | result | log(1+loss) | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Accept |     0.42356 |      1.8227 |    0.037728 |    0.037333 |      0.99911 |         true |
|   22 | Accept |     0.29144 |      2.5086 |    0.037728 |    0.037412 |     0.036437 |        false |
|   23 | Accept |     0.29417 |      3.0408 |    0.037728 |    0.037374 |    0.0028126 |        false |
|   24 | Accept |    0.037926 |      2.5137 |    0.037728 |     0.03734 |      0.13439 |         true |
|   25 | Accept |     0.29417 |      3.1683 |    0.037728 |    0.037309 |    0.0022057 |         true |
|   26 | Best   |    0.037683 |      2.3835 |    0.037683 |    0.037288 |      0.28002 |         true |
|   27 | Accept |     0.29417 |      2.8786 |    0.037683 |    0.037257 |   0.00026057 |        false |
|   28 | Accept |     0.29417 |      3.1422 |    0.037683 |    0.037227 |   0.00025684 |         true |
|   29 | Accept |    0.038598 |      2.1877 |    0.037683 |    0.037245 |      0.12062 |         true |
|   30 | Accept |    0.037686 |      2.1851 |    0.037683 |    0.037261 |      0.30522 |         true |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 100.4694 seconds
Total objective function evaluation time: 75.0054

Best observed feasible point:
     Sigma     Standardize
    _______    ___________

    0.28002       true    

Observed objective function value = 0.037683
Estimated objective function value = 0.036997
Function evaluation time = 2.3835

Best estimated feasible point (according to models):
     Sigma     Standardize
    _______    ___________

    0.13877       false   

Estimated objective function value = 0.037261
Estimated function evaluation time = 2.4607

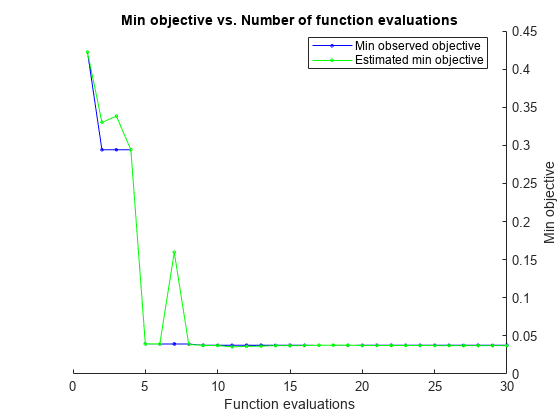
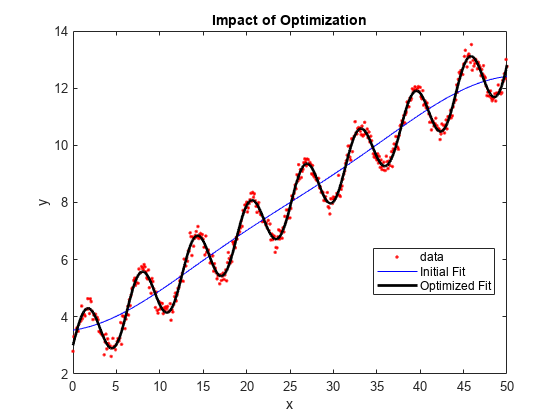
最適化前と最適化後の当てはめを比較します。

ypred1 = resubPredict(gprMdl1);
ypred2 = resubPredict(gprMdl2);

figure();
plot(x,y,'r.');
hold on
plot(x,ypred1,'b');
plot(x,ypred2,'k','LineWidth',2);
xlabel('x');
ylabel('y');
legend({'data','Initial Fit','Optimized Fit'},'Location','Best');
title('Impact of Optimization');
hold off

交差検証の使用による GPR モデルの学習

この例では、UCI Machine Learning Repository [3]にあるアワビのデータ[1]、[2]を使用します。データをダウンロードして、abalone.data という名前で現在のフォルダに保存します。

データを table に格納します。最初の 7 行を表示します。

tbl = readtable('abalone.data','Filetype','text','ReadVariableNames',false);
tbl.Properties.VariableNames = {'Sex','Length','Diameter','Height','WWeight','SWeight','VWeight','ShWeight','NoShellRings'};
tbl(1:7,:)

ans = 

    Sex    Length    Diameter    Height    WWeight    SWeight    VWeight    ShWeight    NoShellRings
    ___    ______    ________    ______    _______    _______    _______    ________    ____________

    'M'    0.455     0.365       0.095      0.514     0.2245      0.101      0.15       15          
    'M'     0.35     0.265        0.09     0.2255     0.0995     0.0485      0.07        7          
    'F'     0.53      0.42       0.135      0.677     0.2565     0.1415      0.21        9          
    'M'     0.44     0.365       0.125      0.516     0.2155      0.114     0.155       10          
    'I'     0.33     0.255        0.08      0.205     0.0895     0.0395     0.055        7          
    'I'    0.425       0.3       0.095     0.3515      0.141     0.0775      0.12        8          
    'F'     0.53     0.415        0.15     0.7775      0.237     0.1415      0.33       20

このデータセットには、4177 個の観測値が含まれています。目標は、8 つの物理的な測定値からアワビの年齢を予測することです。最後の変数は貝殻の輪の数で、アワビの年齢を示します。最初の予測子は、カテゴリカル変数です。テーブルの最後の変数は、応答変数です。

データの 25% を検証用に使用して、交差検証 GPR モデルを学習させます。

rng('default') % For reproducibility
cvgprMdl = fitrgp(tbl,'NoShellRings','Standardize',1,'Holdout',0.25);

分割外観測値で学習させたモデルを使用して、分割の平均損失を計算します。

kfoldLoss(cvgprMdl)

ans =
   4.6409

分割外データの応答を予測します。

ypred = kfoldPredict(cvgprMdl);

検証と予測に使用した真の応答をプロットします。

figure();
plot(ypred(cvgprMdl.Partition.test));
hold on;
y = table2array(tbl(:,end));
plot(y(cvgprMdl.Partition.test),'r.');
axis([0 1050 0 30]);
xlabel('x')
ylabel('y')
hold off;

カスタムなカーネル関数の使用による GPR モデルの当てはめ

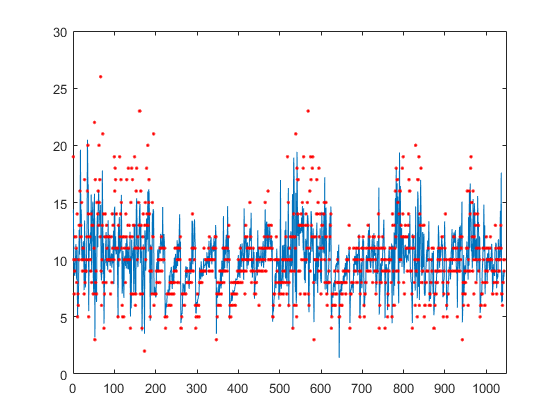
標本データを生成します。

rng(0,'twister'); % For reproducibility
n = 1000;
x = linspace(-10,10,n)';
y = 1 + x*5e-2 + sin(x)./x + 0.2*randn(n,1);

二乗指数カーネル関数をカスタムなカーネル関数として定義します。

二乗指数カーネル関数は、次のように計算できます。

$$k(x_i,x_j|\theta )={\sigma }_f^2\exp (-\frac{1}{2}\frac{(x_i-x_j{)}^T(x_i-x_j)}{{\sigma }_l^2}),$$

ここで、$${\sigma }_f$$ は信号標準偏差、$${\sigma }_l$$ は長さスケールです。$${\sigma }_f$$ と $${\sigma }_l$$ はどちらも 0 より大きくなければなりません。この条件は、制約のないパラメーター表現ベクトル $$\theta$$ について制約のないパラメーター表現 $${\sigma }_l=\exp (\theta (1))$$ および $${\sigma }_f=\exp (\theta (2))$$ を使用することにより適用できます。

したがって、二乗指数カーネル関数は、次のカスタムなカーネル関数として定義できます。

kfcn = @(XN,XM,theta) (exp(theta(2))^2)*exp(-(pdist2(XN,XM).^2)/(2*exp(theta(1))^2));

ここで、pdist2(XN,XM).^2 は距離行列を計算します。

カスタムなカーネル関数 kfcn を使用して、GPR モデルを当てはめます。カーネル パラメーターの初期値を指定します (カスタムなカーネル関数を使用するので、制約のないパラメーター表現ベクトル theta の初期値を指定しなければなりません)。

theta0 = [1.5,0.2];
gprMdl = fitrgp(x,y,'KernelFunction',kfcn,'KernelParameters',theta0);

組み込みカーネル関数の場合、fitrgp はパラメーター推定に解析的微分を使用します。カスタムなカーネル関数の場合は、数値微分を使用します。

このモデルの再代入損失を計算します。

L = resubLoss(gprMdl)

L = 0.0391

組み込まれている二乗指数カーネル関数オプションを使用して、GPR モデルを当てはめます。カーネル パラメーターの初期値を指定します (組み込まれているカスタムなカーネル関数を使用して初期パラメーター値を指定しているので、信号標準偏差と長さスケールの初期値を直接指定しなければなりません)。

sigmaL0 = exp(1.5);
sigmaF0 = exp(0.2);
gprMdl2 = fitrgp(x,y,'KernelFunction','squaredexponential','KernelParameters',[sigmaL0,sigmaF0]);

このモデルの再代入損失を計算します。

L2 = resubLoss(gprMdl2)

L2 = 0.0391

予想どおり、2 つの損失の値は同じです。

LBFGS 最適化の初期ステップ サイズの指定

生成されたデータに対して、多数の予測子を使用して GPR モデルに学習をさせます。LBFGS オプティマイザーの初期ステップ サイズを指定します。

結果に再現性をもたせるために、乱数発生器のシードとタイプを設定します。

rng(0,'twister'); % For reproducibility 

300 個の観測値と 3000 個の予測子がある標本データを生成します。応答変数は 4 番目、7 番目および 13 番目の予測子に依存します。

N = 300;
P = 3000;
X = rand(N,P);
y = cos(X(:,7)) + sin(X(:,4).*X(:,13)) + 0.1*randn(N,1);

カーネル パラメーターの初期値を設定します。

sigmaL0 = sqrt(P)*ones(P,1); % Length scale for predictors
sigmaF0 = 1; % Signal standard deviation

初期ノイズ標準偏差を 1 に設定します。

sigmaN0 = 1;

相対勾配ノルムの終了許容誤差として 1e-2 を指定します。

opts = statset('fitrgp');
opts.TolFun = 1e-2;

初期カーネル パラメーター値、初期ノイズ標準偏差および関連度自動決定 (ARD) 二乗指数カーネル関数を使用して GPR モデルを当てはめます。

LBFGS オプティマイザーにおけるヘッシアンの初期近似を決定するため、初期ステップ サイズとして 1 を指定します。

gpr = fitrgp(X,y,'KernelFunction','ardsquaredexponential','Verbose',1, ...
    'Optimizer','lbfgs','OptimizerOptions',opts, ...
    'KernelParameters',[sigmaL0;sigmaF0],'Sigma',sigmaN0,'InitialStepSize',1);

o Parameter estimation: FitMethod = Exact, Optimizer = lbfgs

 o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|        0 |  3.004966e+02 |   2.569e+02 |   0.000e+00 |        |   3.893e-03 |   0.000e+00 |   YES  |
|        1 |  9.525779e+01 |   1.281e+02 |   1.003e+00 |    OK  |   6.913e-03 |   1.000e+00 |   YES  |
|        2 |  3.972026e+01 |   1.647e+01 |   7.639e-01 |    OK  |   4.718e-03 |   5.000e-01 |   YES  |
|        3 |  3.893873e+01 |   1.073e+01 |   1.057e-01 |    OK  |   3.243e-03 |   1.000e+00 |   YES  |
|        4 |  3.859904e+01 |   5.659e+00 |   3.282e-02 |    OK  |   3.346e-03 |   1.000e+00 |   YES  |
|        5 |  3.748912e+01 |   1.030e+01 |   1.395e-01 |    OK  |   1.460e-03 |   1.000e+00 |   YES  |
|        6 |  2.028104e+01 |   1.380e+02 |   2.010e+00 |    OK  |   2.326e-03 |   1.000e+00 |   YES  |
|        7 |  2.001849e+01 |   1.510e+01 |   9.685e-01 |    OK  |   2.344e-03 |   1.000e+00 |   YES  |
|        8 | -7.706109e+00 |   8.340e+01 |   1.125e+00 |    OK  |   5.771e-04 |   1.000e+00 |   YES  |
|        9 | -1.786074e+01 |   2.323e+02 |   2.647e+00 |    OK  |   4.217e-03 |   1.250e-01 |   YES  |
|       10 | -4.058422e+01 |   1.972e+02 |   6.796e-01 |    OK  |   7.035e-03 |   1.000e+00 |   YES  |
|       11 | -7.850209e+01 |   4.432e+01 |   8.335e-01 |    OK  |   3.099e-03 |   1.000e+00 |   YES  |
|       12 | -1.312162e+02 |   3.334e+01 |   1.277e+00 |    OK  |   5.432e-02 |   1.000e+00 |   YES  |
|       13 | -2.005064e+02 |   9.519e+01 |   2.828e+00 |    OK  |   5.292e-03 |   1.000e+00 |   YES  |
|       14 | -2.070150e+02 |   1.898e+01 |   1.641e+00 |    OK  |   6.817e-03 |   1.000e+00 |   YES  |
|       15 | -2.108086e+02 |   3.793e+01 |   7.685e-01 |    OK  |   3.479e-03 |   1.000e+00 |   YES  |
|       16 | -2.122920e+02 |   7.057e+00 |   1.591e-01 |    OK  |   2.055e-03 |   1.000e+00 |   YES  |
|       17 | -2.125610e+02 |   4.337e+00 |   4.818e-02 |    OK  |   1.974e-03 |   1.000e+00 |   YES  |
|       18 | -2.130162e+02 |   1.178e+01 |   8.891e-02 |    OK  |   2.856e-03 |   1.000e+00 |   YES  |
|       19 | -2.139378e+02 |   1.933e+01 |   2.371e-01 |    OK  |   1.029e-02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       20 | -2.151111e+02 |   1.550e+01 |   3.015e-01 |    OK  |   2.765e-02 |   1.000e+00 |   YES  |
|       21 | -2.173046e+02 |   5.856e+00 |   6.537e-01 |    OK  |   1.414e-02 |   1.000e+00 |   YES  |
|       22 | -2.201781e+02 |   8.918e+00 |   8.484e-01 |    OK  |   6.381e-03 |   1.000e+00 |   YES  |
|       23 | -2.288858e+02 |   4.846e+01 |   2.311e+00 |    OK  |   2.661e-03 |   1.000e+00 |   YES  |
|       24 | -2.392171e+02 |   1.190e+02 |   6.283e+00 |    OK  |   8.113e-03 |   1.000e+00 |   YES  |
|       25 | -2.511145e+02 |   1.008e+02 |   1.198e+00 |    OK  |   1.605e-02 |   1.000e+00 |   YES  |
|       26 | -2.742547e+02 |   2.207e+01 |   1.231e+00 |    OK  |   3.191e-03 |   1.000e+00 |   YES  |
|       27 | -2.849931e+02 |   5.067e+01 |   3.660e+00 |    OK  |   5.184e-03 |   1.000e+00 |   YES  |
|       28 | -2.899797e+02 |   2.068e+01 |   1.162e+00 |    OK  |   6.270e-03 |   1.000e+00 |   YES  |
|       29 | -2.916723e+02 |   1.816e+01 |   3.213e-01 |    OK  |   1.415e-02 |   1.000e+00 |   YES  |
|       30 | -2.947674e+02 |   6.965e+00 |   1.126e+00 |    OK  |   6.339e-03 |   1.000e+00 |   YES  |
|       31 | -2.962491e+02 |   1.349e+01 |   2.352e-01 |    OK  |   8.999e-03 |   1.000e+00 |   YES  |
|       32 | -3.004921e+02 |   1.586e+01 |   9.880e-01 |    OK  |   3.940e-02 |   1.000e+00 |   YES  |
|       33 | -3.118906e+02 |   1.889e+01 |   3.318e+00 |    OK  |   1.213e-01 |   1.000e+00 |   YES  |
|       34 | -3.189215e+02 |   7.086e+01 |   3.070e+00 |    OK  |   8.095e-03 |   1.000e+00 |   YES  |
|       35 | -3.245557e+02 |   4.366e+00 |   1.397e+00 |    OK  |   2.718e-03 |   1.000e+00 |   YES  |
|       36 | -3.254613e+02 |   3.751e+00 |   6.546e-01 |    OK  |   1.004e-02 |   1.000e+00 |   YES  |
|       37 | -3.262823e+02 |   4.011e+00 |   2.026e-01 |    OK  |   2.441e-02 |   1.000e+00 |   YES  |
|       38 | -3.325606e+02 |   1.773e+01 |   2.427e+00 |    OK  |   5.234e-02 |   1.000e+00 |   YES  |
|       39 | -3.350374e+02 |   1.201e+01 |   1.603e+00 |    OK  |   2.674e-02 |   1.000e+00 |   YES  |

|====================================================================================================|
|   ITER   |   FUN VALUE   |  NORM GRAD  |  NORM STEP  |  CURV  |    GAMMA    |    ALPHA    | ACCEPT |
|====================================================================================================|
|       40 | -3.379112e+02 |   5.280e+00 |   1.393e+00 |    OK  |   1.177e-02 |   1.000e+00 |   YES  |
|       41 | -3.389136e+02 |   3.061e+00 |   7.121e-01 |    OK  |   2.935e-02 |   1.000e+00 |   YES  |
|       42 | -3.401070e+02 |   4.094e+00 |   6.224e-01 |    OK  |   3.399e-02 |   1.000e+00 |   YES  |
|       43 | -3.436291e+02 |   8.833e+00 |   1.707e+00 |    OK  |   5.231e-02 |   1.000e+00 |   YES  |
|       44 | -3.456295e+02 |   5.891e+00 |   1.424e+00 |    OK  |   3.772e-02 |   1.000e+00 |   YES  |
|       45 | -3.460069e+02 |   1.126e+01 |   2.580e+00 |    OK  |   3.907e-02 |   1.000e+00 |   YES  |
|       46 | -3.481756e+02 |   1.546e+00 |   8.142e-01 |    OK  |   1.565e-02 |   1.000e+00 |   YES  |

         Infinity norm of the final gradient = 1.546e+00
              Two norm of the final step     = 8.142e-01, TolX   = 1.000e-12
Relative infinity norm of the final gradient = 6.016e-03, TolFun = 1.000e-02
EXIT: Local minimum found.

o Alpha estimation: PredictMethod = Exact

多数の予測子がある ARD カーネルを GPR モデルで使用するので、ヘッシアンに対して LBFGS 近似を使用すると、ヘッセ行列全体を格納するよりメモリ効率が向上します。また、初期ステップ サイズを使用してヘッシアンの初期近似を決定すると、最適化が高速になる可能性があります。

負の学習済み長さスケールの指数を使用して、予測子の重みを求めます。重みを正規化します。

sigmaL = gpr.KernelInformation.KernelParameters(1:end-1); % Learned length scales
weights = exp(-sigmaL); % Predictor weights
weights = weights/sum(weights); % Normalized predictor weights

正規化した予測子の重みをプロットします。

figure;
semilogx(weights,'ro');
xlabel('Predictor index');
ylabel('Predictor weight');

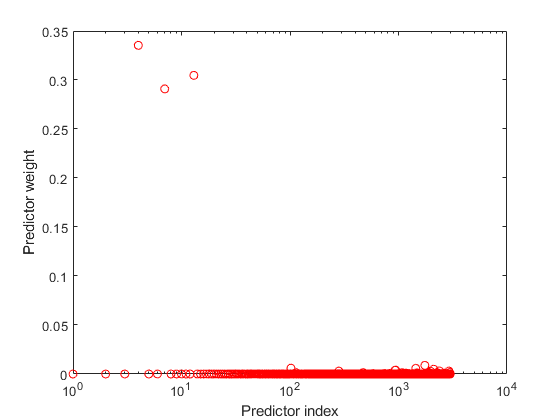
学習済みの GPR モデルは、4 番目、7 番目および 13 番目の予測子に最大の重みを割り当てています。無関係な予測子の重みはゼロに近くなります。

入力引数

Tbl — 標本データ

table

モデルを学習させるために使用する標本データ。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの変数に対応します。Tbl は予測子変数を格納し、応答変数用の 1 列をオプションで含むこともできます。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

• Tbl に応答変数が含まれている場合に他の変数をすべて予測子として使用するには、ResponseVarName を使用して応答変数を指定します。

• Tbl に応答変数が含まれている場合に予測子の一部のみをモデルの学習で使用するには、formula を使用して応答変数と予測子変数を指定します。

• Tbl に応答変数が含まれていない場合は、y を使用して応答変数を指定します。応答変数の長さと Tbl の行数は等しくなければなりません。

table データ型の詳細については、table を参照してください。

カテゴリカル変数が予測子データに含まれている場合、fitrgp はダミー変数を作成します。詳細については、CategoricalPredictors を参照してください。

データ型: table

ResponseVarName — 応答変数名

Tbl 内の変数の名前

応答変数の名前。Tbl 内の変数の名前で指定します。ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 y が Tbl に (Tbl.y として) 格納されている場合、'y' として指定します。それ以外の場合、モデルを学習させるときに、Tbl の列は y を含めてすべて予測子として扱われます。

データ型: char | string

formula — モデルの学習で使用する応答変数と予測子変数

'y~x1+x2+x3' という形式の文字ベクトルまたは string スカラー

モデルの学習で使用する応答変数と予測子変数。'y~x1+x2+x3' という形式の文字ベクトルまたは string スカラーを指定します。この形式では、y は応答変数を、x1、x2 および x3 はモデルの学習で使用する予測子変数を表します。

モデルに学習をさせるときに使用する予測子として、Tbl に含まれている変数の一部を指定するには、式を使用します。式を指定した場合、formula に現れない変数はモデルの学習に使用されません。

式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB^® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。

式で BasisFunction の形式を指定することはできません。

例: 'PetalLength~PetalWidth+Species' は、変数 PetalLength を応答変数として、PetalWidth および Species を予測子変数として特定します。

データ型: char | string

X — GPR モデルの予測子データ

n 行 d 列の行列

GPR モデルの予測子データ。n 行 d 列の行列として指定します。n は観測値 (行) の数、d は予測子 (列) の数です。

y の長さと X の行数は等しくなければなりません。

予測子の名前を X に表示される順序で指定するには、PredictorNames 名前と値のペアの引数を使用します。

データ型: double

y — GPR モデルの応答データ

n 行 1 列のベクトル

GPR モデルの応答データ。n 行 1 列のベクトルとして指定します。y も含まれている学習データ Tbl を指定した場合、y を省略できます。この場合、ResponseVarName を使用して応答変数を特定するか、formula を使用して応答変数および予測子変数を特定します。

データ型: double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'FitMethod','sr','BasisFunction','linear','ActiveSetMethod','sgma','PredictMethod','fic' は、パラメーターの推定に回帰変数サブセット近似法、基底関数として線形基底関数、アクティブ セットの選択にスパース グリーディ行列近似法、および予測に完全独立条件近似法を使用して GPR モデルを学習させます。

メモ

交差検証の名前と値の引数は、名前と値の引数 'OptimizeHyperparameters' と一緒には使用できません。'OptimizeHyperparameters' の場合の交差検証は、名前と値の引数 'HyperparameterOptimizationOptions' を使用することのみによって変更できます。

近似

FitMethod — GPR モデルのパラメーター推定方式

"none" | "exact" | "sd" | "sr" | "fic"

GPR モデルのパラメーター推定方式。次のいずれかとして指定します。

近似方式	説明
"none"	推定を行いません。初期パラメーター値を既知のパラメーター値として使用します。
"exact"	厳密なガウス過程回帰。この値は n ≤ 2000 の場合の既定値です。ここで、n は観測値の数です。
"sd"	データ点サブセット近似。この値は n > 2000 の場合の既定値です。ここで、n は観測値の数です。"sd" はスパース法です。
"sr"	回帰変数サブセット近似。"sr" はスパース法です。
"fic"	完全独立条件近似。"fic" はスパース法です。

例: FitMethod="fic"

BasisFunction — GPR モデルの明示的な基底関数

"constant" (既定値) | "none" | "linear" | "pureQuadratic" | 関数ハンドル

GPR モデルの明示的な基底関数。"constant"、"none"、"linear"、"pureQuadratic"、または関数ハンドルとして指定します。観測値の数が n の場合、基底関数は H*β という項をモデルに追加します。ここで、H は基底行列、β は p 行 1 列の基底係数のベクトルです。

明示的な基底関数	基底行列
"none"	空行列
"constant"	$$H=1$$ H は n 行 1 列の 1 のベクトルで、n は観測値の数です。
"linear"	$$H=[1,X]$$ X はカテゴリカル変数のダミー変数が作成された後の展開された予測子データです。ダミー変数の作成に関する詳細については、CategoricalPredictors を参照してください。
"pureQuadratic"	$$H=\left[1,X,X_2\right],$$ ここで $$X_2=\left[\begin{array}{cccc}{x}_{11}^2& x_{12}^2& \cdots & x_{1d}^2\\ x_{21}^2& x_{22}^2& \cdots & x_{2d}^2\\ ⋮& ⋮& ⋮& ⋮\\ x_{n1}^2& x_{n2}^2& \cdots & x_{nd}^2\end{array}\right].$$ この基底オプションでは、カテゴリカル予測子をもつ X はサポートされません。
関数ハンドル	fitrgp で次のように呼び出す関数ハンドル hfcn。 $$H=hfcn(X),$$ ここで、X は n 行 d 列の予測子の行列、d はカテゴリカル変数のダミー変数が作成された後の予測子の数、H は n 行 p 列の基底関数の行列です。

例: BasisFunction="pureQuadratic"

データ型: char | string | function_handle

Beta — 係数の初期値

p 行 1 列のベクトル

明示的な基底関数の係数の初期値。p 行 1 列のベクトルとして指定します。p は、基底行列 "H" の列数です。

基底行列は、指定された基底関数によって決まります。詳細については、BasisFunction を参照してください。

FitMethod が "none" の場合のみ、学習関数は係数の初期値を既知の係数値として使用します。

データ型: double

Sigma — ノイズ標準偏差の初期値

std(y)/sqrt(2) (既定値) | 正のスカラー値

ガウス過程モデルのノイズ標準偏差の初期値。正のスカラー値として指定します。

学習関数は、SigmaLowerBound および exp(η) の合計としてノイズ標準偏差をパラメーター化します。ここで η は制約なしの値です。したがって、関数が η を有限値に初期化できるように、Sigma は小さい許容誤差だけ SigmaLowerBound よりも大きい必要があります。そうでない場合、関数は Sigma を互換性のある値にリセットします。

許容誤差は ConstantSigma が false (既定) の場合 1e-3 です。それ以外の場合は 1e-6 です。許容誤差が応答変数のスケールに対して十分小さくない場合、この許容誤差の値が応答変数に対して小さいと見なせるように、応答変数を拡大できます。

例: Sigma=2

データ型: double

ConstantSigma — ノイズ標準偏差に対する定数値の Sigma

false または 0 (既定値) | true または 1

ガウス過程モデルのノイズ標準偏差に対する定数値の Sigma。数値または logical の 0 (false) または 1 (true) として指定します。ConstantSigma が true の場合、学習関数は Sigma の値を最適化せず、計算全体で初期値を使用します。

例: ConstantSigma=true

データ型: logical

SigmaLowerBound — ノイズ標準偏差の下限

1e-2*std(y) (既定値) | 正のスカラー値

ノイズ標準偏差 (Sigma) の下限。正のスカラー値として指定します。

Sigma は小さい許容誤差だけ SigmaLowerBound よりも大きい必要があります。

例: SigmaLowerBound=0.02

データ型: double

CategoricalPredictors — カテゴリカル予測子のリスト

正の整数のベクトル | logical ベクトル | 文字行列 | string 配列 | 文字ベクトルの cell 配列 | 'all'

カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。

値	説明
正の整数のベクトル	ベクトルの各エントリは、対応する予測子がカテゴリカルであることを示すインデックス値です。インデックス値の範囲は 1 ～ p です。p はモデルの学習に使用した予測子の数です。 fitrgp が入力変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。応答変数、観測値の重みの変数、および関数で使用されないその他の変数は、CategoricalPredictors 値でカウントされません。
logical ベクトル	true というエントリは、対応する予測子がカテゴリカルであることを意味します。ベクトルの長さは p です。
文字行列	行列の各行は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。文字行列の各行が同じ長さになるように、名前を余分な空白で埋めてください。
文字ベクトルの cell 配列または string 配列	配列の各要素は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。
"all"	すべての予測子がカテゴリカルです。

既定では、予測子データがテーブル (Tbl) 内にある場合、fitrgp は、その変数が logical ベクトル、categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。予測子データが行列 (X) である場合、fitrgp はすべての予測子が連続的であると見なします。他の予測子をカテゴリカル予測子として指定するには、名前と値の引数 CategoricalPredictors を使用してそれらを指定します。

特定されたカテゴリカル予測子に対して、fitrgp はカテゴリカル変数に順序が設定されていないか順序が設定されているかに応じて、2 つの異なる方式を使用してダミー変数を作成します。順序付けのないカテゴリカル変数の場合、fitrgp は、そのカテゴリカル変数の各レベルについて 1 つずつダミー変数を作成します。順序付けされたカテゴリカル変数の場合、fitrgp は、カテゴリの数よりも 1 つ少ないダミー変数を作成します。詳細については、ダミー変数の自動作成を参照してください。

例: 'CategoricalPredictors','all'

データ型: single | double | logical | char | string | cell

Standardize — データ標準化インジケーター

false または 0 (既定値) | true または 1

データを標準化するためのインジケーター。数値または logical の 0 (false) または 1 (true) として指定します。

Standardize=1 を設定すると、予測子データの各列が列の平均と標準偏差でセンタリングおよびスケーリングされます。カテゴリカル予測子について生成されたダミー変数の列に格納されているデータは標準化されません。

例: Standardize=1

例: Standardize=true

データ型: logical

Regularization — 正則化標準偏差

1e-2*std(y) (既定値) | 正のスカラー値

回帰変数サブセット ("sr") および完全独立条件 ("fic") の近似法の正則化標準偏差。正のスカラー値として指定します。詳細については、FitMethod を参照してください。

例: Regularization=0.2

データ型: double

ComputationMethod — 対数尤度と勾配を計算する方式

"qr" (既定値) | "v"

パラメーター推定の対数尤度と勾配を計算する方式。"qr" または "v" として指定します。この引数は、FitMethod が "sr" または "fic" の場合に有効です。

• "qr" — QR 分解に基づくアプローチを使用します。精度が高くなります。

• "v" — V 方式に基づくアプローチを使用します。計算が速くなります。

これらのアプローチの詳細については、Foster らの[7]を参照してください。

例: ComputationMethod="v"

カーネル (共分散) 関数

KernelFunction — 共分散関数の形式

"squaredexponential" (既定値) | "exponential" | "matern32" | "matern52" | "rationalquadratic" | "ardsquaredexponential" | "ardexponential" | "ardmatern32" | "ardmatern52" | "ardrationalquadratic" | 関数ハンドル

共分散関数の形式。次のいずれかを指定します。

値	説明
"exponential"	指数カーネル
"squaredexponential"	二乗指数カーネル
"matern32"	パラメーターが 3/2 の Matern カーネル
"matern52"	パラメーターが 5/2 の Matern カーネル
"rationalquadratic"	有理二次カーネル
"ardexponential"	予測子ごとに長さスケールが異なる指数カーネル
"ardsquaredexponential"	予測子ごとに長さスケールが異なる二乗指数カーネル
"ardmatern32"	パラメーターが 3/2 で予測子ごとに長さスケールが異なる Matern カーネル
"ardmatern52"	パラメーターが 5/2 で予測子ごとに長さスケールが異なる Matern カーネル
"ardrationalquadratic"	予測子ごとに長さスケールが異なる有理二次カーネル
関数ハンドル	次の形式の関数ハンドル。 Kmn = kfcn(Xm,Xn,theta) ここで、Xm は m 行 d 列の行列、Xn は n 行 d 列の行列、Kmn は Kmn(i,j) が Xm(i,:) と Xn(j,:) の間のカーネル積である m 行 n 列のカーネル積の行列です。d はカテゴリカル変数のダミー変数が作成された後の予測子変数の数です。ダミー変数の作成の詳細については、CategoricalPredictors を参照してください。 theta は kfcn についての制約がない r 行 1 列のパラメーター ベクトルです。

カーネル関数についての詳細は、カーネル (共分散) 関数のオプションを参照してください。

例: KernelFunction="matern32"

データ型: char | string | function_handle

KernelParameters — カーネル パラメーターの初期値

数値ベクトル

カーネル パラメーターの初期値。数値ベクトルとして指定します。ベクトルのサイズと値は、名前と値の引数 KernelFunction で指定する共分散間数の形式によって異なります。

KernelFunction Value	KernelParameters Value
"exponential"、"squaredexponential"、"matern32"、または "matern52"	2 行 1 列のベクトル phi。phi(1) には長さスケールを、phi(2) には信号標準偏差を格納します。 長さスケール パラメーターの既定の初期値は予測子の標準偏差の平均です。信号標準偏差は応答の標準偏差を 2 の平方根で除算した値です。つまり、次のようになります。 phi = [mean(std(X));std(y)/sqrt(2)]。
"rationalquadratic"	3 行 1 列のベクトル phi。phi(1) には長さスケールを、phi(2) にはスケール混合パラメーターを、phi(3) には信号標準偏差を格納します。 長さスケール パラメーターの既定の初期値は予測子の標準偏差の平均です。信号標準偏差は応答の標準偏差を 2 の平方根で除算した値です。スケール混合パラメーターの既定の初期値は 1 です。つまり、次のようになります。 phi = [mean(std(X));1;std(y)/sqrt(2)]。
"ardexponential"、"ardsquaredexponential"、"ardmatern32"、または "ardmatern52"	(d+1) 行 1 列のベクトル phi。phi(i) には予測子 i の長さスケールを、phi(d+1) には信号標準偏差を格納します。d は、カテゴリカル変数用にダミー変数が作成された後の予測子変数の数です。ダミー変数の作成に関する詳細については、CategoricalPredictors を参照してください。 長さスケール パラメーターの既定の初期値は予測子の標準偏差です。信号標準偏差は応答の標準偏差を 2 の平方根で除算した値です。つまり、次のようになります。 phi = [std(X)';std(y)/sqrt(2)]。
"ardrationalquadratic"	(d+2) 行 1 列のベクトル phi。phi(i) には予測子 i の長さスケール、phi(d+1) にはスケール混合パラメーターを、phi(d+2) には信号標準偏差を格納します。d は、カテゴリカル変数用にダミー変数が作成された後の予測子変数の数です。ダミー変数の作成の詳細については、CategoricalPredictors を参照してください。 長さスケール パラメーターの既定の初期値は予測子の標準偏差です。信号標準偏差は応答の標準偏差を 2 の平方根で除算した値です。スケール混合パラメーターの既定の初期値は 1 です。つまり、次のようになります。 phi = [std(X)';1;std(y)/sqrt(2)]。
関数ハンドル	カスタム カーネル関数 kfcn の非制約パラメーター ベクトル phi の初期値の r 行 1 列のベクトル。 KernelFunction が関数ハンドルの場合、カーネル パラメーターの初期値を指定しなければなりません。

カーネル関数についての詳細は、カーネル (共分散) 関数のオプションを参照してください。

例: KernelParameters=phi

データ型: double | single

DistanceMethod — 点間の距離を計算する方式

"fast" (既定値) | "accurate"

組み込みカーネル関数を評価するために点間の距離を計算する方式。"fast" または "accurate" として指定します。"fast" を指定すると、学習関数は $${\left(x-y\right)}^2$$ を $$x^2+y^2-2*x*y$$ として計算します。"accurate" を指定すると、学習関数は $${\left(x-y\right)}^2$$ を計算します。

例: DistanceMethod="accurate"

アクティブ セットの選択

ActiveSet — アクティブ セット内の観測値

[] (既定値) | 1 から n の範囲にある整数が含まれている m 行 1 列のベクトル (m ≤ n) | 長さが n の logical ベクトル

アクティブ セット内の観測値。1 から n の範囲にある整数から成る m 行 1 列のベクトル (m ≤ n)、または少なくとも 1 つの true 要素が含まれている長さが n の logical ベクトルとして指定します。n は、学習データに含まれている観測値の総数です。

fitrgp では、ActiveSet で指定された観測値を使用して GPR モデルを学習させます。重複する要素をアクティブ セットに含めることはできません。

ActiveSet を指定した場合、次のようになります。

• fitrgp は、ActiveSetSize と ActiveSetMethod を使用しません。

• このモデルに対して交差検証を実行できません。

データ型: double | logical

ActiveSetSize — アクティブ セットのサイズ

整数 m (1 ≤ m ≤ n)

アクティブ セットのサイズ。整数 m (1 ≤ m ≤ n) として指定します。ここで、n は観測値の数です。この引数は、FitMethod が "sd"、"sr"、または "fic" の場合に有効です。

既定値は、FitMethod が "sr" または "fic" の場合は min(1000,n)、それ以外の場合は min(2000,n) です。

例: ActiveSetSize=100

データ型: double

ActiveSetMethod — アクティブ セット選択法

"random" (既定値) | "sgma" | "entropy" | "likelihood"

アクティブ セット選択法。次の値のいずれかとして指定します。

値	説明
"random"	無作為選択
"sgma"	スパース グリーディ行列近似
"entropy"	微分エントロピーに基づく選択
"likelihood"	回帰変数サブセットの対数尤度に基づく選択

("random" を除く) すべてのアクティブ セット選択法で、格納場所として n 行 m 列の行列が必要です。ここで、m はアクティブ セットのサイズ、n は観測値の数です。

例: ActiveSetMethod="entropy"

RandomSearchSetSize — ランダム探索セットのサイズ

59 (既定値) | 整数値

アクティブ セットを選択するためのグリーディな包含におけるランダム探索セットのサイズ。整数値として指定します。

例: RandomSearchSetSize=30

データ型: double

ToleranceActiveSet — アクティブ セットの選択を終了させるための相対許容誤差

1e-06 (既定値) | 正のスカラー

アクティブ セットの選択を終了させるための相対許容誤差。正のスカラーとして指定します。

例: ToleranceActiveset=0.0002

データ型: double

NumActiveSetRepeats — 反復数

3 (既定値) | 整数値

ActiveSetMethod が "random" ではない場合の、インターリーブ方式によるアクティブ セット選択とパラメーター推定における反復の数。整数値として指定します。

例: NumActiveSetRepeats=5

データ型: double

予測

PredictMethod — 予測を行うための方式

"exact" | "bcd" | "sd" | "sr" | "fic"

与えられたパラメーターに対してガウス過程モデルで予測を行うために使用する方式。次の値のいずれかとして指定します。

値	説明
"exact"	厳密ガウス過程回帰法。この値は n ≤ 10,000 の場合の既定値です。
"bcd"	ブロック座標降下 (BCD)。この値は n > 10,000 の場合の既定値です。
"sd"	データ点サブセット近似
"sr"	回帰変数サブセット近似
"fic"	完全独立条件近似

例: PredictMethod="bcd"

BlockSizeBCD — BCD 法のブロック サイズ

1000 または n の小さい方の値 (既定値) | 1 から n までの範囲の整数

ブロック座標降下法 ("bcd") のブロック サイズ。1 から n までの範囲の整数として指定します。ここで、n は観測値の数です。

例: BlockSizeBCD=1500

データ型: double

NumGreedyBCD — BCD 法のグリーディ選択の数

100 と BlockSizeBCD の小さい方の値 (既定値) | 1 から BlockSizeBCD までの範囲の整数値

ブロック座標降下法 ("bcd") のグリーディ選択の数。1 から BlockSizeBCD までの範囲の整数として指定します。

例: NumGreedyBCD=150

データ型: double

ToleranceBCD — 勾配ノルムの相対許容誤差

1e-3 (既定値) | 正のスカラー

ブロック座標降下法 ("bcd") の反復を終了させるための勾配ノルムの相対許容誤差。正のスカラーとして指定します。

例: ToleranceBCD=0.002

データ型: double

StepToleranceBCD — ステップ サイズの絶対許容誤差

1e-3 (既定値) | 正のスカラー

ブロック座標降下法 ("bcd") の反復を終了させるためのステップ サイズの絶対許容誤差。正のスカラーとして指定します。

例: StepToleranceBCD=0.002

データ型: double

IterationLimitBCD — BCD の最大反復数

1000000 (既定値) | 正の整数

ブロック座標降下法 ("bcd") の最大反復数。正の整数として指定します。

例: IterationLimitBCD=10000

データ型: double

最適化

Optimizer — パラメーター推定に使用するオプティマイザ―

'quasinewton' (既定値) | 'lbfgs' | 'fminsearch' | 'fminunc' | 'fmincon'

パラメーター推定に使用するオプティマイザー。次の表にある値のいずれかを指定します。

値	説明
'quasinewton'	ヘッシアンに対する、密で対称的なランク 1 に基づく準ニュートン近似
'lbfgs'	ヘッシアンに対する、LBFGS に基づく準ニュートン近似
'fminsearch'	Lagarias らのシンプレックス探索法 [5] を使用する、制約がない非線形最適化
'fminunc'	制約がない非線形最適化 (Optimization Toolbox™ のライセンスが必要)
'fmincon'	制約がある非線形最適化 (Optimization Toolbox のライセンスが必要)

オプティマイザーの詳細については、アルゴリズムを参照してください。

例: 'Optimizer','fmincon'

OptimizerOptions — オプティマイザーのオプション

構造体 | オブジェクト

名前と値の引数 Optimizer で設定されるオプティマイザーのオプション。optimset、statset("fitrgp")、または optimoptions によって作成された構造体またはオブジェクトとして指定します。

オプティマイザー	オプティマイザーのオプションを作成する関数
"fminsearch"	optimset (構造体)
"quasinewton" または "lbfgs"	statset("fitrgp") (構造体)
"fminunc" または "fmincon"	optimoptions (オブジェクト)

既定のオプションは、指定されたオプティマイザーによって異なります。

例: OptimizerOptions=opt

InitialStepSize — 初期ステップ サイズ

[] (既定値) | 正の実数スカラー | "auto"

初期ステップ サイズ。正の実数スカラーまたは "auto" として指定します。

InitialStepSize は、オプティマイザーが "quasinewton" または "lbfgs" である場合の最初の最適化ステップにおける近似値の絶対値の最大値です。初期ステップ サイズにより、最適化におけるヘッシアンの初期近似を決定できます。

既定では、学習関数はヘッシアンの初期近似の決定に初期ステップ サイズを使用しません。初期ステップ サイズを使用するには、名前と値の引数 InitialStepSize の値を設定するか、InitialStepSize="auto" を指定して値を自動的に決定させます。"auto" の詳細については、アルゴリズムを参照してください。

例: InitialStepSize="auto"

交差検証

CrossVal — 交差検証のインジケーター

'off' (既定値) | 'on'

交差検証のインジケーター。'off' または 'on' のいずれかを指定します。'on' の場合、fitrgp は 10 分割で交差検証した GPR モデルを返します。

名前と値のペアの引数 KFold、Holdout、Leaveout または CVPartition のいずれかを使用すると、既定の交差検証の設定を変更できます。これらの名前と値のペアの引数は、一度に 1 つだけ使用できます。

代替方法として、モデルに対して crossval メソッドを使用できます。

例: 'CrossVal','on'

CVPartition — 層化 k 分割交差検証用の無作為な分割

cvpartition オブジェクト

層化 k 分割交差検証用の無作為な分割。cvpartition オブジェクトとして指定します。

例: 'CVPartition',cvp では、cvp によって定義される無作為な分割を使用します。

CVPartition を指定する場合、Holdout、KFold または Leaveout のいずれも指定できません。

Holdout — 検証に使用するデータの比率

0 から 1 の範囲にあるスカラー値

ホールドアウト検証で検定に使用するデータの比率。範囲 0 から 1 のスカラー値として指定します。'Holdout',p を指定すると、次が実行されます。
1.データの約 p*100% を検証データとして無作為に予約し、残りのデータを使用してモデルに学習させる。
2. コンパクトな学習済みモデルを cvgprMdl.Trained に格納する。

例: 'Holdout', 0.3 では、データの 30% を検証に、70% を学習に使用します。

Holdout を指定する場合、CVPartition、KFold または Leaveout のいずれも指定できません。

データ型: double

KFold — 分割の数

10 (既定値) | 正の整数値

交差検証 GPR モデルで使用する分割の数。正の整数値として指定します。KFold は 1 より大きくなければなりません。'KFold',k を指定すると、次が実行されます。
1.データを無作為に k 個のセットに分割する。
2. 各セットについて、そのセットをテスト データとして予約し、他の k - 1 個のセットを使用してモデルを学習させる。
3. k 個のコンパクトな学習済みモデルを cvgprMdl.Trained 内の k 行 1 列の cell 配列のセルに格納する。

例: 'KFold',5 では、5 つの分割を交差検証で使用します。つまり、各分割について、その分割をテスト データとして使用し、残りの 4 つの分割でモデルを学習させます。

KFold を指定する場合、CVPartition、Holdout または Leaveout のいずれも指定できません。

データ型: double

Leaveout — leave-one-out 交差検証のインジケーター

'off' (既定値) | 'on'

leave-one-out 交差検証のインジケーター。'off' または 'on' のいずれかを指定します。

'Leaveout','on' を指定する場合、n 個の観測値のそれぞれについて以下が行われます。
1. 観測値はテスト データとして予約され、モデルは他の n – 1 個の観測値を使用して学習させる。
2. コンパクトな学習済みモデルを n 行 1 列の cell 配列 cvgprMdl.Trained のセルに格納する。

例: 'Leaveout','on'

Leaveout を指定する場合、CVPartition、Holdout または KFold のいずれも指定できません。

ハイパーパラメーターの最適化

OptimizeHyperparameters — 最適化するパラメーター

'none' (既定値) | 'auto' | 'all' | 使用可能パラメーター名の string 配列または cell 配列 | optimizableVariable オブジェクトのベクトル

最適化するパラメーター。次のいずれかを指定します。

• 'none' — 最適化を行いません。

• 'auto' — {'Sigma','Standardize'} を使用します。

• 'all' — すべての使用可能パラメーターを最適化します。{'BasisFunction','KernelFunction','KernelScale','Sigma','Standardize'} と同じです。

• 使用可能パラメーター名の string 配列または cell 配列。

• optimizableVariable オブジェクトのベクトル。通常は hyperparameters の出力です。

最適化では、パラメーターを変化させることにより、fitrgp の交差検証損失 (誤差) を最小化しようとします。交差検証のタイプおよびその他の最適化の側面を制御するには、名前と値のペア HyperparameterOptimizationOptions を使用します。

メモ

OptimizeHyperparameters の値は、他の名前と値の引数を使用して指定した値より優先されます。たとえば、OptimizeHyperparameters を "auto" に設定すると、fitrgp は "auto" オプションに対応するハイパーパラメーターを最適化して、ハイパーパラメーターに指定された値を無視します。

fitrgp では、以下のパラメーターを使用できます。

• BasisFunction — fitrgp は、'constant'、'none'、'linear' および 'pureQuadratic' で探索します。

• KernelFunction — fitrgp は、'ardexponential'、'ardmatern32'、'ardmatern52'、'ardrationalquadratic'、'ardsquaredexponential'、'exponential'、'matern32'、'matern52'、'rationalquadratic' および 'squaredexponential' で探索します。

• KernelScale — fitrgp は、引数 KernelParameters を使用してカーネル スケール パラメーターの値を指定します。この値は、当てはめ時に変化しません。この場合、すべての入力次元は KernelScale の値が同じになるように制約されます。fitrgp は範囲 [1e-3,1e3] の対数スケールで正の値を探索します。

  どの ARD カーネルについても KernelScale を最適化することはできません。

• Sigma — fitrgp は、範囲 [1e-4,max(1e-3,10*ResponseStd)] の対数スケールで正の値を探索します。ここで、次のようになります。

  ResponseStd = std(y).

  内部的に、fitrgp は名前と値のペア ConstantSigma を true に設定するので、当てはめ時に Sigma の値は定数になります。

• Standardize — fitrgp は true と false で探索します。

既定以外のパラメーターを設定するには、既定以外の値が含まれている optimizableVariable オブジェクトのベクトルを渡します。たとえば、以下のようにします。

load fisheriris
params = hyperparameters('fitrgp',meas,species);
params(1).Range = [1e-4,1e6];

OptimizeHyperparameters の値として params を渡します。

既定では、コマンド ラインに反復表示が表示され、最適化のハイパーパラメーターの個数に従ってプロットが表示されます。最適化とプロットにおける目的関数は、log(1 + cross-validation loss) です。反復表示を制御するには、名前と値の引数 'HyperparameterOptimizationOptions' の Verbose フィールドを設定します。プロットを制御するには、名前と値の引数 'HyperparameterOptimizationOptions' の ShowPlots フィールドを設定します。

たとえば、GPR 回帰の最適化を参照してください。

例: 'auto'

HyperparameterOptimizationOptions — 最適化のオプション

構造体

最適化のオプション。構造体として指定します。この引数を指定すると、名前と値の引数 OptimizeHyperparameters の効果が変化します。この構造体のフィールドは、すべてオプションです。

フィールド名	値	既定の設定
Optimizer	'bayesopt' — ベイズ最適化を使用。内部的には bayesopt が呼び出されます。 'gridsearch' — 次元ごとに NumGridDivisions の値があるグリッド探索を使用。 'randomsearch' — MaxObjectiveEvaluations 個の点で無作為に探索。 'gridsearch' では、グリッドからの一様な非復元抽出により、無作為な順序で探索します。最適化後、sortrows(Mdl.HyperparameterOptimizationResults) コマンドを使用してグリッド順のテーブルを取得できます。	'bayesopt'
AcquisitionFunctionName	'expected-improvement-per-second-plus' 'expected-improvement' 'expected-improvement-plus' 'expected-improvement-per-second' 'lower-confidence-bound' 'probability-of-improvement' オブジェクト関数のランタイムによって最適化が異なるので、名前に per-second が含まれている獲得関数は、再現性がある結果を生成しません。名前に plus が含まれている獲得関数は、領域を過剰利用している場合に動作を変更します。詳細は、獲得関数のタイプを参照してください。	'expected-improvement-per-second-plus'
MaxObjectiveEvaluations	目的関数評価の最大数。	'bayesopt' および 'randomsearch' の場合は 30、'gridsearch' の場合はグリッド全体
MaxTime	制限時間。正の実数スカラーを指定します。制限時間の単位は、tic と toc によって測定される秒です。MaxTime は関数評価を中断させないため、実行時間が MaxTime を超える可能性があります。	Inf
NumGridDivisions	'gridsearch' における各次元の値の個数。値は、各次元の値の個数を表す正の整数のベクトル、またはすべての次元に適用されるスカラーが可能です。カテゴリカル変数の場合、このフィールドは無視されます。	10
ShowPlots	プロットを表示するかどうかを示す論理値。true の場合、最良の観測された目的関数の値が反復回数に対してプロットされます。ベイズ最適化を使用する場合 (Optimizer が 'bayesopt')、最良の推定された目的関数値もプロットされます。最良の観測された目的関数値および最良の推定された目的関数値は、反復表示の BestSoFar (observed) 列および BestSoFar (estim.) 列の値にそれぞれ対応しています。これらの値は、Mdl.HyperparameterOptimizationResults のプロパティ ObjectiveMinimumTrace および EstimatedObjectiveMinimumTrace で確認できます。問題にベイズ最適化の最適化パラメーターが 1 つまたは 2 つある場合、ShowPlots はパラメーターに対する目的関数のモデルもプロットします。	true
SaveIntermediateResults	Optimizer が 'bayesopt' である場合に結果を保存するかどうかを示す論理値。true の場合、'BayesoptResults' という名前のワークスペース変数が反復ごとに上書きされます。この変数は BayesianOptimization オブジェクトです。	false
Verbose	コマンド ラインに次を表示します。 0 — 反復表示なし 1 — 反復表示あり 2 — 追加情報付きで反復表示あり 詳細については、bayesopt の名前と値の引数 Verbose およびベイズ最適化の使用による分類器の当てはめの最適化の例を参照してください。	1
UseParallel	ベイズ最適化を並列実行するかどうかを示す論理値。並列実行には Parallel Computing Toolbox™ が必要です。並列でのタイミングに再現性がないため、並列ベイズ最適化で再現性のある結果が生成されるとは限りません。詳細については、並列ベイズ最適化を参照してください。	false
Repartition	反復ごとに交差検証を再分割するかどうかを示す論理値。false の場合、オプティマイザーは単一の分割を最適化に使用します。 分割ノイズが考慮されるので、通常は true に設定すると最も確実な結果が得られます。ただし、true で良好な結果を得るには、2 倍以上の関数評価が必要になります。	false
以下の 3 つのオプションは 1 つだけ使用できます。
CVPartition	cvpartition によって作成される cvpartition オブジェクト	交差検証フィールドが指定されていない場合 'Kfold',5
Holdout	ホールドアウトの比率を表す範囲 (0,1) のスカラー
Kfold	1 より大きい整数

例: 'HyperparameterOptimizationOptions',struct('MaxObjectiveEvaluations',60)

データ型: struct

その他

PredictorNames — 予測子変数名

一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

予測子変数名。一意な名前の string 配列または一意な文字ベクトルの cell 配列として指定します。'PredictorNames' の機能は、学習データの提供方法によって決まります。

• X と y を指定した場合、'PredictorNames' を使用して X の名前で予測子変数を指定できます。

  • PredictorNames 内の名前の順序は、X の列の順序に一致しなければなりません。つまり、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前であり、他も同様です。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。

  • 既定では PredictorNames は {'x1','x2',...} です。

• Tbl が与えられた場合、'PredictorNames' を使用して学習に使用する予測子変数を選択できます。つまり、fitrgp は PredictorNames の予測子変数と応答のみを学習で使用します。

  • PredictorNames は Tbl.Properties.VariableNames のサブセットでなければならず、応答変数の名前を含めることはできません。

  • 既定では、すべての予測子変数の名前が PredictorNames に格納されます。

  • 'PredictorNames' と formula のいずれか一方のみを使用して学習用の予測子を指定することをお勧めします。

例: 'PredictorNames',{'PedalLength','PedalWidth'}

データ型: string | cell

ResponseName — 応答変数名

"Y" (既定値) | 文字ベクトル | string スカラー

応答変数名。文字ベクトルまたは string スカラーとして指定します。

• Y を指定した場合、ResponseName を使用して応答変数の名前を指定できます。

• ResponseVarName または formula を指定した場合、ResponseName を使用できません。

例: "ResponseName","response"

データ型: char | string

Verbose — 詳細レベル

0 (既定値) | 1

詳細レベル。0 または 1 として指定します。

• 0 — 学習関数は、アクティブ セットの選択とブロック座標降下に関連する診断メッセージを表示しませんが、OptimizerOptions の Display の値によってはパラメーター推定に関連するメッセージを表示します。

• 1 ― 学習関数は、パラメーター推定、アクティブ セットの選択、およびブロック座標降下に関連する診断メッセージを繰り返し表示します。

例: Verbose=1

CacheSize — メガバイト単位のキャッシュ サイズ

1000 (既定値) | 正のスカラー

メガバイト (MB) 単位のキャッシュ サイズ。正のスカラーとして指定します。キャッシュ サイズは、当てはめとアクティブ セット選択に必要とされるメモリに加えて使用可能な追加のメモリです。学習関数は次の目的に CacheSize を使用します。

• パラメーター推定時に点間の距離をキャッシュするかどうかの決定。

• ブロック座標降下法および予測実施における行列ベクトル積の計算方法の決定。

例: CacheSize=2000

データ型: double

出力引数

gprMdl — ガウス過程回帰モデル

RegressionGP オブジェクト | RegressionPartitionedGP オブジェクト

ガウス過程回帰モデル。RegressionGP オブジェクトまたは RegressionPartitionedGP オブジェクトとして返されます。

• 交差検証を行った場合、つまり、名前と値の引数 'Crossval'、'KFold'、'Holdout'、'Leaveout' または 'CVPartition' を使用した場合、gprMdl は RegressionPartitionedGP オブジェクトになります。kfoldPredict を使用して、学習時に fitrgp がホールドアウトした観測値の応答を予測できます。kfoldPredict は、各観測値の応答をその観測値を使用せずに学習させたモデルを使用して予測します。交差検証済みモデルについて予測区間を計算することはできません。

• 交差検証を行わなかった場合、gprMdl は RegressionGP オブジェクトになります。predict を使用して新しい観測値の応答を予測し、resubPredict を使用して学習観測値の応答を予測できます。predict および resubPredict を使用して、予測区間も計算できます。

詳細

アクティブ セットの選択とパラメーターの推定

データ サブセット近似法、回帰変数サブセット近似法または完全独立条件近似法の場合 (FitMethod が 'sd'、'sr' または 'fic' に等しい場合) にアクティブ セット (または誘導入力セット) を指定しないと、fitrgp は一連の反復でアクティブ セットを選択してパラメーター推定を計算します。

1 回目の反復では、ベクトル η₀ = [β₀,σ₀,θ₀] の初期パラメーター値を使用して、アクティブ セット A₁ を選択します。η₀ (初期値) と A₁ を使用して GPR の周辺対数尤度または近似を最大化することにより、新しいパラメーター推定 η₁ を計算します。次に、η₁ と A₁ を使用して、新しい対数尤度 L₁ を計算します。

2 回目の反復では、η₁ のパラメーター値を使用して、アクティブ セット A₂ を選択します。次に、η₁ (初期値) と A₂ を使用して、GPR の周辺対数尤度または近似を最大化し、新しいパラメーター値 η₂ を推定します。さらに、η₂ と A₂ を使用して、新しい対数尤度値 L₂ を計算します。

次の表は、各反復とその計算をまとめたものです。

反復数	アクティブ セット	パラメーター ベクトル	対数尤度
1	A1	η1	L1
2	A2	η2	L2
3	A3	η3	L3
…	…	…	…

指定した回数の繰り返しについて、同様に反復処理が行われます。アクティブ セット選択の反復回数は、名前と値の引数 NumActiveSetRepeats を使用して指定できます。

ヒント

• fitrgp は、近似法、予測法およびアクティブ セット選択法についてどのような組み合わせでも受け入れます。予測した応答の標準偏差を計算できないために予測区間を計算できない場合があります。predict を参照してください。また、学習データのサイズのため、厳密法を使用すると計算コストが高くなる場合もあります。

• PredictorNames プロパティには、元の予測子変数名のそれぞれについて 1 つずつ要素が格納されます。たとえば、3 つの予測子があり、そのうちの 1 つは 3 つの水準があるカテゴリカル変数である場合、PredictorNames は 1 行 3 列の文字ベクトルの cell 配列になります。

• ExpandedPredictorNames プロパティには、ダミー変数を含む予測子変数のそれぞれについて 1 つずつ要素が格納されます。たとえば、3 つの予測子があり、そのうちの 1 つは 3 つの水準があるカテゴリカル変数である場合、ExpandedPredictorNames は 1 行 5 列の文字ベクトルの cell 配列になります。

• 同様に、Beta プロパティには、ダミー変数を含む各予測子について 1 つずつベータ係数が格納されます。

• X プロパティには、はじめに入力した状態で学習データが格納されます。ダミー変数は含まれません。

• 多数の予測子がある ARD カーネルを使用する場合など、GPR モデルに多数のカーネル パラメーターがある場合、fitrgp でヘッシアン近似を初期化する既定のアプローチは低速になる可能性があります。このような場合は、'auto' または初期ステップ サイズの値を指定することを検討します。

  反復的診断メッセージの表示に 'Verbose',1 を設定し、fitrgp による既定の最適化で LBFGS または準ニュートン オプティマイザーを使用して GPR モデルによる学習を始めることができます。数秒後になっても反復的な診断メッセージが表示されない場合、ヘッシアン近似の初期化に時間がかかりすぎている可能性があります。このような場合は、学習をやり直し、最適化を高速化するために初期ステップ サイズを使用することを検討します。

• モデルに学習をさせた後で、新しいデータについて応答を予測する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。

アルゴリズム

• GPR モデルの当てはめでは、次のモデル パラメーターをデータから推定します。

  • ベクトル $$\theta$$ 内のカーネル パラメーターに関してパラメーター化された共分散関数 $$k\left(x_i,x_j|\theta \right)$$ (カーネル (共分散) 関数のオプションを参照)

  • ノイズ分散 $${\sigma }^2$$

  • 固定基底関数の係数ベクトル $$\beta$$

  名前と値の引数 KernelParameters の値は、信号標準偏差 $${\sigma }_f$$ と特性長スケール $${\sigma }_l$$ の初期値から構成されるベクトルです。これらの値を使用してカーネル パラメーターが決定されます。同様に、名前と値の引数 Sigma にはノイズ標準偏差 $$\sigma$$ の初期値が格納されます。

• 最適化時に、ノイズ標準偏差とカーネル パラメーターの初期値を使用して、制約がない初期パラメーター値のベクトル $${\eta }_0$$ が作成されます。

• 名前と値の引数 Beta によって指定された明示的な基底係数 $$\beta$$ が $$\theta$$ と $${\sigma }^2$$ の推定値から解析的に決定されます。したがって、数値最適化を初期化するときに $$\beta$$ はベクトル $${\eta }_0$$ に現れません。

  メモ

  GPR モデルのパラメーター推定を指定しなかった場合、名前と値の引数 Beta の値と他の初期パラメーター値が既知の GPR パラメーター値として使用されます (Beta を参照)。他のすべてのケースでは、Beta の値は目的関数から解析的に最適化されます。

• 準ニュートン オプティマイザーでは、密で対称的なランク 1 に基づく (SR1) 準ニュートン近似による信頼領域法をヘッシアンに対して使用します。LBFGS オプティマイザーでは、メモリ制限 Broyden-Fletcher-Goldfarb-Shanno (LBFGS) 準ニュートン近似による標準的な直線探索法をヘッシアンに対して使用します。Nocedal および Wright [6] を参照してください。

• 名前と値の引数 InitialStepSize を "auto" に設定した場合、$${\Vert s_0\Vert }_{\infty }=0.5{\Vert {\eta }_0\Vert }_{\infty }+0.1$$ を使用して初期ステップ サイズ $${\Vert s_0\Vert }_{\infty }$$ が決定されます。

  $$s_0$$ は初期ステップ ベクトル、$${\eta }_0$$ は制約がない初期パラメーター値のベクトルです。

• 最適化時に、初期ステップ サイズ $${\Vert s_0\Vert }_{\infty }$$ が次のように使用されます。

  Optimizer="quasinewton" と初期ステップ サイズを指定した場合、ヘッシアンの初期近似は $$\frac{{\Vert g_0\Vert }_{\infty }}{{\Vert s_0\Vert }_{\infty }}I$$ になります。

  Optimizer="lbfgs" と初期ステップ サイズを指定した場合、逆ヘッシアンの初期近似は $$\frac{{\Vert s_0\Vert }_{\infty }}{{\Vert g_0\Vert }_{\infty }}I$$ になります。

  $$g_0$$ は初期勾配ベクトル、$$I$$ は単位行列です。

参照

[1] Nash, W.J., T. L. Sellers, S. R. Talbot, A. J. Cawthorn, and W. B. Ford. "The Population Biology of Abalone (Haliotis species) in Tasmania. I. Blacklip Abalone (H. rubra) from the North Coast and Islands of Bass Strait." Sea Fisheries Division, Technical Report No. 48, 1994.

[2] Waugh, S. "Extending and Benchmarking Cascade-Correlation: Extensions to the Cascade-Correlation Architecture and Benchmarking of Feed-forward Supervised Artificial Neural Networks." University of Tasmania Department of Computer Science thesis, 1995.

[3] Lichman, M. UCI Machine Learning Repository, Irvine, CA: University of California, School of Information and Computer Science, 2013. http://archive.ics.uci.edu/ml.

[4] Rasmussen, C. E. and C. K. I. Williams. Gaussian Processes for Machine Learning. MIT Press. Cambridge, Massachusetts, 2006.

[5] Lagarias, J. C., J. A. Reeds, M. H. Wright, and P. E. Wright. "Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions." SIAM Journal of Optimization. Vol. 9, Number 1, 1998, pp. 112–147.

[6] Nocedal, J. and S. J. Wright. Numerical Optimization, Second Edition. Springer Series in Operations Research, Springer Verlag, 2006.

拡張機能

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

ハイパーパラメーターの最適化を並列実行するには、関数 fitrgp を呼び出すときに名前と値の引数 'HyperparameterOptimizationOptions', struct('UseParallel',true) を指定します。

並列的なハイパーパラメーターの最適化の詳細については、並列ベイズ最適化を参照してください。

並列計算の全般的な情報については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2015b で導入

R2023b: OptimizeHyperparameters の "auto" オプションに Standardize を追加

R2023b 以降では、OptimizeHyperparameters の値として "auto" を指定した場合、fitrgp には最適化可能なハイパーパラメーターとして Standardize が含まれます。

R2023b: GPR モデルの最適化で KernelScale ハイパーパラメーターの検索範囲が予測子データに依存しない

R2023b 以降では、fitrgp でガウス過程回帰 (GPR) モデルのカーネル スケール パラメーターを最適化する際に既定の検索範囲 [1e-3,1e3] が使用されます。つまり、名前と値の引数 OptimizeHyperparameters を使用して GPR のハイパーパラメーター KernelScale を最適化するように指定すると、関数は範囲 [1e-3,1e3] の対数スケールで正の値を探索します。

以前のリリースでは、KernelScale ハイパーパラメーターについての既定の検索範囲は [1e-3*MaxPredictorRange,MaxPredictorRange] で、MaxPredictorRange = max(max(X) - min(X)) でした。

R2022b: 交差検証ガウス過程回帰モデルは RegressionPartitionedGP オブジェクト

R2022b 以降では、交差検証ガウス過程回帰 (GPR) モデルは RegressionPartitionedGP オブジェクトです。以前のリリースでは、交差検証 GPR モデルは RegressionPartitionedModel オブジェクトでした。

RegressionPartitionedGP オブジェクトは 2 つの方法で作成できます。

• オブジェクト関数 crossval を使用して、GPR モデル オブジェクト RegressionGP から交差検証済みモデルを作成する。

• 関数 fitrgp を使用し、名前と値の引数 CrossVal、CVPartition、Holdout、KFold、Leaveout のいずれかを指定して、交差検証済みモデルを作成する。

最初に GPR モデルの完全なモデルと交差検証済みモデルのどちらに学習させるかに関係なく、fitrgp の呼び出しで ActiveSet の値を指定することはできません。

参考

RegressionGP | predict | compact

トピック

• ガウス過程回帰モデル
• カーネル (共分散) 関数のオプション
• 特徴選択の紹介