LIME を使用した表形式データに関する深層ネットワークの予測の解釈

この例では、Locally Interpretable Model-agnostic Explanations (LIME) 技術を使用し、表形式データの分類を行う深層ニューラル ネットワークの予測を解釈する方法を説明します。LIME 技術を使用して、ネットワークによる分類の判定に最も重要な予測子を把握できます。

この例では、LIME を使用して、特徴データ分類用のネットワークを解釈します。指定されたクエリ観測値に対して、LIME は、各特徴の統計量が実データ セットと一致する合成データ セットを生成します。この合成データ セットは、分類を取得するために深層ニューラル ネットワークに渡され、単純かつ解釈しやすいモデルが当てはめられます。この単純なモデルは、ネットワークの分類判定に対する上位のいくつかの特徴量の重要度を理解するために使用できます。この解釈可能モデルの学習において、合成観測値はクエリ観測値からの距離で重み付けされます。そのため、説明はクエリ観測値に対して "局所的" になります。

この例では、lime (Statistics and Machine Learning Toolbox)とfit (Statistics and Machine Learning Toolbox)を使用して合成データ セットを生成し、単純かつ解釈可能なモデルを合成データ セットに当てはめます。学習済みのイメージ分類ニューラル ネットワークによる予測を理解するには、imageLIMEを使用してください。詳細については、LIME を使用したネットワーク予測の理解を参照してください。

データの読み込み

フィッシャーのアヤメのデータ セットを読み込みます。このデータには 150 個の観測値のほかに、植物のパラメーターを表す 4 つの入力特徴と、植物の種類を表す 1 つのカテゴリカル応答が含まれています。各観測値は、3 種類 (setosa、versicolor、virginica) のいずれかに分類されます。各観測値には、4 つの測定値 (がく片の幅、がく片の長さ、花弁の幅、花弁の長さ) があります。

filename = fullfile(toolboxdir('stats'),'statsdata','fisheriris.mat');
load(filename)

数値データを table に変換します。

features = ["Sepal length","Sepal width","Petal length","Petal width"];

predictors = array2table(meas,"VariableNames",features);
trueLabels = array2table(categorical(species),"VariableNames","Response");

最後の列を応答とする学習データの table を作成します。

data = [predictors trueLabels];

観測値の数、特徴の数、およびクラスの数を計算します。

numObservations = size(predictors,1);
numFeatures = size(predictors,2);
classNames = categories(data{:,5});
numClasses = length(classNames);

学習セット、検証セット、およびテスト セットへのデータの分割

データ セットを学習セット、検証セット、およびテスト セットに分割します。データの 15% を検証用に、15% をテスト用に残しておきます。

各区画の観測数を求めます。乱数シードを設定してデータを分割し、CPU での学習が再現可能になるようにします。

rng('default');
numObservationsTrain = floor(0.7*numObservations);
numObservationsValidation = floor(0.15*numObservations);

観測値に対応するランダムなインデックスの配列を作成し、区画サイズを使用して分割します。

idx = randperm(numObservations);
idxTrain = idx(1:numObservationsTrain);
idxValidation = idx(numObservationsTrain + 1:numObservationsTrain + numObservationsValidation);
idxTest = idx(numObservationsTrain + numObservationsValidation + 1:end);

インデックスを使用して、データの table を学習用、検証用、およびテスト用の区画に分割します。

dataTrain = data(idxTrain,:);
dataVal = data(idxValidation,:);
dataTest = data(idxTest,:);

ネットワーク アーキテクチャの定義

5 個のニューロンと ReLU 活性化がある 1 つの隠れ層をもつ単純な多層パーセプトロンを作成します。特徴入力層は、フィッシャーのアヤメのデータ セットのような、特徴量を表す数値スカラーを含むデータを受け入れます。

numHiddenUnits = 5;
layers = [
    featureInputLayer(numFeatures)
    fullyConnectedLayer(numHiddenUnits)
    reluLayer
    fullyConnectedLayer(numClasses)
    softmaxLayer];

学習オプションの定義とネットワークの学習

モーメンタム項付き確率的勾配降下 (SGDM) を使用してネットワークに学習させます。学習データに含まれている観測値の数は多くないため、最大エポック数を 30 に設定し、ミニバッチのサイズ 15 を使用します。

opts = trainingOptions("sgdm", ...
    MaxEpochs=30, ...
    MiniBatchSize=15, ...
    Shuffle="every-epoch", ...
    ValidationData=dataVal, ...
    Metrics="accuracy",...
    ExecutionEnvironment="cpu");

関数trainnetを使用してニューラル ネットワークに学習させます。分類には、クロスエントロピー損失を使用します。

net = trainnet(dataTrain,layers,"crossentropy",opts);

    Iteration    Epoch    TimeElapsed    LearnRate    TrainingLoss    ValidationLoss    TrainingAccuracy    ValidationAccuracy
    _________    _____    ___________    _________    ____________    ______________    ________________    __________________
            0        0       00:00:03         0.01                            1.4077                                    31.818
            1        1       00:00:04         0.01          1.1628                                46.667                      
           50        8       00:00:04         0.01         0.50707           0.36361              86.667                90.909
          100       15       00:00:05         0.01         0.19781           0.25353              86.667                90.909
          150       22       00:00:05         0.01         0.26973           0.19193              86.667                95.455
          200       29       00:00:06         0.01         0.20914           0.18269              86.667                90.909
          210       30       00:00:06         0.01          0.3616           0.15335              73.333                95.455
Training stopped: Max epochs completed

ネットワーク性能の評価

学習済みネットワークを使用してテスト セットの観測値を分類します。複数の観測値を使用して予測を行うには、関数minibatchpredictを使用します。予測スコアをラベルに変換するには、関数 scores2label を使用します。関数 minibatchpredict は利用可能な GPU がある場合に自動的にそれを使用します。GPU を使用するには、Parallel Computing Toolbox™ ライセンスとサポートされている GPU デバイスが必要です。サポートされているデバイスについては、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。そうでない場合、関数は CPU を使用します。

scores = minibatchpredict(net,dataTest(:,1:4));
predictedLabels = scores2label(scores,classNames);
trueLabels = dataTest{:,end};

混同行列を使用して結果を可視化します。

figure
confusionchart(trueLabels,predictedLabels)

ネットワークは、テスト観測値について、植物の 4 つの特徴を使用して種類をうまく予測できています。

クラスごとに異なる予測子を使用することの重要性について理解する

LIME を使用して、ネットワークの分類判定に対する各予測子の重要度を理解します。

各観測値の最も重要な 2 つの予測子について調査します。

numImportantPredictors = 2;

lime を使用して、各特徴の統計量が実データ セットと一致する合成データ セットを作成します。深層学習モデル blackbox と、predictors に含まれている予測子データを使用して lime オブジェクトを作成します。'KernelWidth' に小さな値を使用して、lime が、クエリ点に近接するサンプルに焦点が当たるような重みを使用するようにします。

blackbox = @(x)scores2label(minibatchpredict(net,x),classNames);
explainer = lime(blackbox,predictors,'Type','classification','KernelWidth',0.1);

この LIME explainer を使用して、深層ニューラル ネットワークに対して最も重要な特徴を理解できます。関数は、クエリ観測値の近傍にあるニューラル ネットワークを近似する単純な線形モデルを使用して、特徴量の重要度を推定します。

setosa クラスに対応するテスト データ内の、最初の 2 つの観測値のインデックスを検索します。

trueLabelsTest = dataTest{:,end};
label = "setosa";
idxSetosa = find(trueLabelsTest == label,2);

関数 fit を使用して、指定されたクラスの最初の 2 つの観測値に単純な線形モデルを当てはめます。

explainerObs1 = fit(explainer,dataTest(idxSetosa(1),1:4),numImportantPredictors);
explainerObs2 = fit(explainer,dataTest(idxSetosa(2),1:4),numImportantPredictors);

結果をプロットします。

figure
subplot(2,1,1)
plot(explainerObs1);
subplot(2,1,2)
plot(explainerObs2);

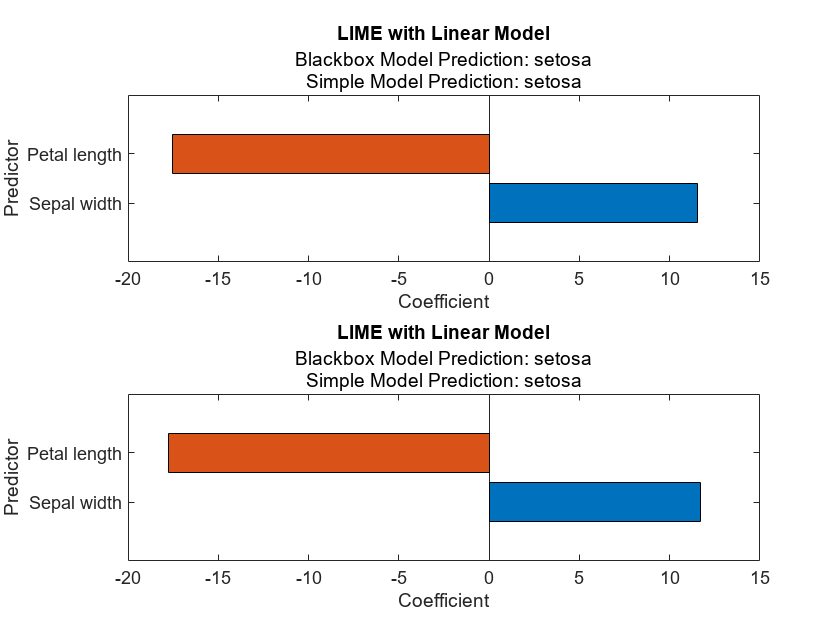
setosa クラスで最も重要な予測子は、小さな値の花弁の長さ (Petal length) と大きな値のがく片の幅 (Sepal width) です。

versicolor クラスに対して同じ解析を実行します。

label = "versicolor";
idxVersicolor = find(trueLabelsTest == label,2);

explainerObs1 = fit(explainer,dataTest(idxVersicolor(1),1:4),numImportantPredictors);
explainerObs2 = fit(explainer,dataTest(idxVersicolor(2),1:4),numImportantPredictors);

figure
subplot(2,1,1)
plot(explainerObs1);
subplot(2,1,2)
plot(explainerObs2);

versicolor クラスでは、大きな値の花弁の長さが重要です。

最後に、virginica クラスについて考慮します。

label = "virginica";
idxVirginica = find(trueLabelsTest == label,2);

explainerObs1 = fit(explainer,dataTest(idxVirginica(1),1:4),numImportantPredictors);
explainerObs2 = fit(explainer,dataTest(idxVirginica(2),1:4),numImportantPredictors);

figure
subplot(2,1,1)
plot(explainerObs1);
subplot(2,1,2)
plot(explainerObs2);

virginica クラスでは、大きな値の花弁の長さと小さな値のがく片の幅が重要です。

LIME 仮説の検証

LIME によるプロットは、花弁の長さの値が大きいものは versicolor と virginica のクラスと関連があり、花弁の長さの値が小さいものは setosa クラスと関連があることを示しています。データの詳細を調べて、結果についてさらに調査できます。

データ セットの各イメージの花弁の長さをプロットします。

setosaIdx = ismember(data{:,end},"setosa");
versicolorIdx = ismember(data{:,end},"versicolor");
virginicaIdx = ismember(data{:,end},"virginica");

figure
hold on
plot(data{setosaIdx,"Petal length"},'.')
plot(data{versicolorIdx,"Petal length"},'.')
plot(data{virginicaIdx,"Petal length"},'.')
hold off

xlabel("Observation number")
ylabel("Petal length")
legend(["setosa","versicolor","virginica"])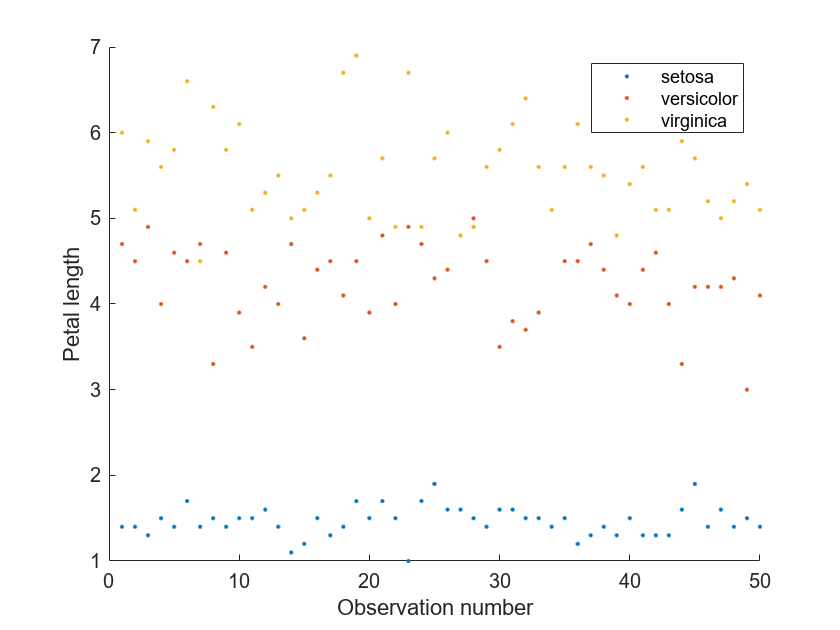

setosa クラスの花弁の長さの値は他のクラスの値をはるかに下回っており、lime モデルから得られた結果と一致しています。

参考

fit (Statistics and Machine Learning Toolbox) | lime (Statistics and Machine Learning Toolbox) | trainnet | trainingOptions | dlnetwork | minibatchpredict | scores2label | featureInputLayer | imageLIME

関連するトピック

• LIME を使用したネットワーク予測の理解
• Investigate Spectrogram Classifications Using LIME
• Grad-CAM での深層学習による判定の理由の解明
• Interpret Deep Learning Time-Series Classifications Using Grad-CAM
• 深層学習の可視化手法