incrementalClassificationLinear

インクリメンタル学習用のバイナリ分類線形モデル

説明

incrementalClassificationLinear は incrementalClassificationLinear モデルオブジェクトを作成します。これは、インクリメンタル学習用のバイナリ分類線形モデルを表します。サポートされる学習器には、サポートベクターマシン (SVM) とロジスティック回帰が含まれます。

他の Statistics and Machine Learning Toolbox™ モデルオブジェクトとは異なり、incrementalClassificationLinear は直接呼び出すことができます。また、モデルをデータに当てはめる前に、パフォーマンスメトリクス構成、パラメーター値、および目的ソルバーなどの学習オプションを指定できます。incrementalClassificationLinear オブジェクトを作成すると、インクリメンタル学習用に準備されます。

incrementalClassificationLinear は、インクリメンタル学習に最適です。バイナリ分類用の SVM または線形モデルに学習させるための従来のアプローチ (データへの当てはめによるモデルの作成、交差検証の実行、ハイパーパラメーターの調整など) については、fitcsvm または fitclinear を参照してください。マルチクラスのインクリメンタル学習については、incrementalClassificationECOC および incrementalClassificationNaiveBayes を参照してください。

作成

incrementalClassificationLinear モデルオブジェクトは、次のいくつかの方法で作成できます。

関数の直接呼び出し — インクリメンタル学習オプションを構成するか、incrementalClassificationLinear を直接呼び出して、線形モデルパラメーターとハイパーパラメーターの初期値を指定します。このアプローチは、データがまだない場合やインクリメンタル学習をすぐに開始したい場合に最適です。
従来式の学習済みモデルの変換 — 学習済みモデルオブジェクトのモデル係数およびハイパーパラメーターを使用して、インクリメンタル学習用のバイナリ分類線形モデルを初期化するには、従来式の学習済みモデルを関数 incrementalLearner に渡して incrementalClassificationLinear モデルオブジェクトに変換できます。この表には、適切なリファレンスページへのリンクが含まれています。

変換可能なモデルオブジェクト変換関数
ClassificationSVM または CompactClassificationSVM incrementalLearner
ClassificationLinear incrementalLearner
テンプレートオブジェクトの変換 — テンプレートオブジェクトを関数 incrementalLearner に渡して incrementalClassificationLinear モデルオブジェクトに変換できます。この表には、適切なリファレンスページへのリンクが含まれています。

変換可能なテンプレートオブジェクト変換関数
templateSVM incrementalLearner
templateLinear incrementalLearner
インクリメンタル学習関数の呼び出し — fit、updateMetrics、および updateMetricsAndFit は、構成済みの incrementalClassificationLinear モデルオブジェクトおよびデータを入力として受け入れ、入力モデルとデータから学習した情報で更新された incrementalClassificationLinear モデルオブジェクトを返します。

変換可能なモデルオブジェクト	変換関数
`ClassificationSVM` または `CompactClassificationSVM`	`incrementalLearner`
`ClassificationLinear`	`incrementalLearner`

変換可能なテンプレートオブジェクト	変換関数
`templateSVM`	`incrementalLearner`
`templateLinear`	`incrementalLearner`

構文

Mdl = incrementalClassificationLinear()

Mdl = incrementalClassificationLinear(Name=Value)

説明

Mdl = incrementalClassificationLinear() は、バイナリ線形分類用の既定のインクリメンタル学習モデルオブジェクト Mdl を返します。既定のモデルのプロパティには、未知のモデルパラメーター用のプレースホルダーが含まれています。既定のモデルは、パフォーマンスを追跡したり、予測を生成したりする前に学習させなければなりません。

例

Mdl = incrementalClassificationLinear(Name=Value) は、名前と値の引数を使用して、プロパティと追加のオプションを設定します。それぞれの名前は引用符で囲みます。たとえば、incrementalClassificationLinear(Beta=[0.1 0.3],Bias=1,MetricsWarmupPeriod=100) は、線形モデル係数 β のベクトルを [0.1 0.3] に、バイアス β₀ を 1 に、およびメトリクスのウォームアップ期間を 100 に設定します。

例

名前と値の引数

すべて展開する

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: Standardize=true は、推定期間中に推定された予測子の平均と標準偏差を使用して、予測子データを標準化します。

`Metrics` — インクリメンタル学習中に追跡するモデルのパフォーマンスメトリクス
`"classiferror"` (既定値) | string ベクトル | 関数ハンドル | cell ベクトル | 構造体配列 | `"binodeviance"` | `"exponential"` | `"hinge"` | `"logit"` | `"quadratic"`

インクリメンタル学習中に追跡するモデルのパフォーマンスメトリクス。組み込みの損失関数の名前、名前の string ベクトル、関数ハンドル (@metricName)、関数ハンドルの構造体配列、または名前、関数ハンドル、構造体配列の cell ベクトルとして指定します。

Mdl が "ウォーム" のとき (IsWarm を参照)、updateMetrics および updateMetricsAndFit は Mdl の Metrics プロパティのパフォーマンスメトリクスを追跡します。

次の表は、組み込みの損失関数名の一覧です。string ベクトルを使用して、複数指定できます。

名前	説明
`"binodeviance"`	二項分布からの逸脱度
`"classiferror"`	分類誤差
`"exponential"`	指数
`"hinge"`	ヒンジ
`"logit"`	ロジスティック
`"quadratic"`	2 次

組み込み損失関数の詳細については、loss を参照してください。

例: 'Metrics',["classiferror" "hinge"]

パフォーマンスメトリクスを返すカスタム関数を指定するには、関数ハンドル表記を使用します。関数は次の形式でなければなりません。

metric = customMetric(C,S)

出力引数 metric は n 行 1 列の数値ベクトルです。ここで、各要素は、学習サイクル中にインクリメンタル学習関数によって処理されたデータの対応する観測値の損失です。
関数名 (customMetric) を指定します。
C は n 行 2 列の logical 行列であり、対応する観測値が属するクラスを各行が示します。列の順序は ClassNames プロパティのクラスの順序に対応します。C を作成するには、指定されたデータの各観測値について観測値 p がクラス q に属する場合に C(p,q) = 1 を設定します。行 p の他の要素を 0 に設定します。
S は、予測分類スコアの n 行 2 列の数値行列です。S は predict の出力 score に似ています。ここで、行はデータの観測値に対応し、列の順序は ClassNames プロパティのクラスの順序に対応しています。S(p,q) は、クラス q に分類されている観測値 p の分類スコアです。

複数のカスタムメトリクスを指定し、それぞれにカスタム名を割り当てるには、構造体配列を使用します。組み込みメトリクスとカスタムメトリクスの組み合わせを指定するには、cell ベクトルを使用します。

例: 'Metrics',struct('Metric1',@customMetric1,'Metric2',@customMetric2)

例: 'Metrics',{@customMetric1 @customMetric2 'logit' struct('Metric3',@customMetric3)}

updateMetrics および updateMetricsAndFit は、table で指定したメトリクスを Metrics プロパティに保存します。Metrics のデータ型によって、table の行名が決まります。

`'Metrics'` 値のデータ型	`Metrics` プロパティの行名の説明	例
string または文字ベクトル	対応する組み込みメトリクスの名前	`"classiferror"` の行名は `"ClassificationError"`
構造体配列	フィールド名	`struct('Metric1',@customMetric1)` の行名は `"Metric1"`
プログラムファイルに格納されている関数への関数ハンドル	関数名	`@customMetric` の行名は `"customMetric"`
無名関数	`CustomMetric_j`。ここで、`j` は `Metrics` のメトリクス `j`	`@(C,S)customMetric(C,S)...` の行名は `CustomMetric_1`

パフォーマンスメトリクスオプションの詳細については、パフォーマンスメトリクスを参照してください。

データ型: char | string | struct | cell | function_handle

`Standardize` — 予測子データを標準化するためのフラグ
`'auto'` (既定値) | `false` | `true`

予測子データを標準化するためのフラグ。次の表の値として指定します。

値	説明
`'auto'`	`incrementalClassificationLinear` が予測子変数を標準化する必要があるかどうかを決定します。データの標準化を参照してください。
`true`	ソフトウェアが予測子データを標準化します。詳細は、データの標準化を参照してください。
`false`	ソフトウェアが予測子データを標準化しません。

例: 'Standardize',true

データ型: logical | char | string

`Shuffle` — 観測値のシャッフルフラグ
`true` (既定値) | `false`

各反復での観測値のシャッフルフラグ。次の表の値として指定します。

値	説明
`true`	ソフトウェアが、関数 `fit` でモデルを当てはめる前に、データの入力チャンク内の観測値をシャッフルします。このアクションにより、抽出スキームによって誘発されるバイアスが低減されます。
`false`	ソフトウェアが、受信した順序でデータを処理します。

このオプションは、Solver が 'scale-invariant' である場合のみ有効です。Solver が 'sgd' または 'asgd' である場合は、データを処理する前に、データの入力チャンク内の観測値が常にシャッフルされます。

例: 'Shuffle',false

データ型: logical

プロパティ

すべて展開する

ほとんどのプロパティは、incrementalClassificationLinear を呼び出すときに名前と値の引数の構文のみを使用して直接設定できます。incrementalLearner を呼び出して従来式の学習済みモデルオブジェクトまたはモデルテンプレートオブジェクトに変換するときに、いくつかのプロパティを設定できます。プロパティ FittedLoss、NumTrainingObservations、Mu、Sigma、SolverOptions、および IsWarm は設定できません。

分類モデルのパラメーター

`Beta` — 線形モデル係数 β
読み取り専用: 数値ベクトル

このプロパティは読み取り専用です。

線形モデル係数 β。NumPredictors 行 1 列の数値ベクトルとして指定します。

インクリメンタル近似関数は学習中に Beta を推定します。Beta の既定の初期値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルオブジェクトまたはテンプレートモデルオブジェクトを変換して Mdl を作成する場合、初期値はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、初期値は zeros(NumPredictors,1) です。

データ型: single | double

`Bias` — モデル切片 β₀
読み取り専用: 数値スカラー

このプロパティは読み取り専用です。

モデル切片 β₀ またはバイアス項。数値スカラーとして指定します。

インクリメンタル近似関数は学習中に Bias を推定します。Bias の既定の初期値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルオブジェクトまたはテンプレートモデルオブジェクトを変換して Mdl を作成する場合、初期値はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、初期値は 0 です。

データ型: single | double

`ClassNames` — 一意のクラスラベル
読み取り専用: categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

このプロパティは読み取り専用です。

モデルの学習に使用される一意のクラスラベル。categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列として指定します。ClassNames と応答データは同じデータ型でなければなりません。(string 配列は文字ベクトルの cell 配列として扱われます)。

ClassNames の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルを変換して Mdl を作成する場合、ClassNames は従来式の学習済みモデルの対応するプロパティによって指定されます。
それ以外の場合、インクリメンタル近似関数は学習中に ClassNames を推測します。

`FittedLoss` — 線形モデルの当てはめに使用する損失関数
読み取り専用: `'hinge'` | `'logit'`

このプロパティは読み取り専用です。

線形モデルの当てはめに使用する損失関数。'hinge' または 'logit' を指定します。

値	アルゴリズム	損失関数	`Learner` の値
`'hinge'`	サポートベクターマシン	ヒンジ: $ℓ [y, f (x)] = \max [0, 1 - y f (x)]$	`'svm'`
`'logit'`	ロジスティック回帰	逸脱度 (ロジスティック): $ℓ [y, f (x)] = \log {1 + \exp [- y f (x)]}$	`'logistic'`

`Learner` — 線形分類モデルのタイプ
読み取り専用: `'svm'` | `'logistic'`

このプロパティは読み取り専用です。

線形分類モデルのタイプ。'svm' または 'logistic' として指定します。incrementalClassificationLinear は Learner 値を文字ベクトルとして格納します。

次の表では $f (x) = x β + b .$ です。

β は p 個の係数のベクトルです。
x は p 個の予測子変数による観測値です。
b はスカラーバイアスです。

値	アルゴリズム	損失関数	`FittedLoss` の値
`'svm'`	サポートベクターマシン	ヒンジ: $ℓ [y, f (x)] = \max [0, 1 - y f (x)]$	`'hinge'`
`'logistic'`	ロジスティック回帰	逸脱度 (ロジスティック): $ℓ [y, f (x)] = \log {1 + \exp [- y f (x)]}$	`'logit'`

Learner の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済み SVM 分類モデルオブジェクト (ClassificationSVM または CompactClassificationSVM) か SVM モデルテンプレートオブジェクト (templateSVM から返されるオブジェクト) を変換して Mdl を作成する場合、Learner は 'svm' になります。
従来式の学習済み線形分類モデルオブジェクト (ClassificationLinear) か線形分類モデルテンプレートオブジェクト (templateLinear から返されるオブジェクト) を変換して Mdl を作成する場合、Learner はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、既定値は 'svm' です。

データ型: char | string

`NumPredictors` — 予測子変数の数
読み取り専用: 非負の数値スカラー

このプロパティは読み取り専用です。

予測子変数の数。非負の数値スカラーとして指定します。

NumPredictors の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルを変換して Mdl を作成する場合、NumPredictors は従来式の学習済みモデルの対応するプロパティによって指定されます。
incrementalClassificationLinear を直接呼び出して Mdl を作成する場合、NumPredictors は名前と値の引数の構文を使用して指定できます。
それ以外の場合、既定値は 0 で、インクリメンタル近似関数は学習中に予測子データから NumPredictors を推測します。

データ型: double

`NumTrainingObservations` — インクリメンタルモデルに当てはめる観測値の数
読み取り専用: `0` (既定値) | 非負の数値スカラー

このプロパティは読み取り専用です。

インクリメンタルモデル Mdl に当てはめる観測値の数。非負の数値スカラーとして指定します。NumTrainingObservations は、Mdl および学習データを fit または updateMetricsAndFit に渡すときに増加します。

メモ

従来式の学習済みモデルを変換して Mdl を作成する場合、incrementalClassificationLinear は、従来式の学習済みモデルに当てはめる観測値の数を NumTrainingObservations に追加しません。

データ型: double

`Prior` — 事前クラス確率
読み取り専用: `'empirical'` | `'uniform'` | 数値ベクトル

このプロパティは読み取り専用です。

クラスの事前確率。'empirical'、'uniform'、または数値ベクトルとして指定します。incrementalClassificationLinear は Prior 値を数値ベクトルとして格納します。

値	説明
`'empirical'`	インクリメンタル学習関数が、インクリメンタル学習中 (推定期間 `EstimationPeriod` の後) に応答データで観測されたクラスの相対頻度から事前クラス確率を推定します。
`'uniform'`	各クラスの事前確率を 1/2 とします。
数値ベクトル	正規化されたカスタム事前確率。`Prior` の要素の順序は `ClassNames` プロパティの要素に対応します。

Prior の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルを変換して Mdl を作成する場合、Prior は従来式の学習済みモデルの対応するプロパティによって指定されます。
それ以外の場合、既定値は 'empirical' です。

データ型: single | double | char | string

`ScoreTransform` — スコア変換関数
読み取り専用: 文字ベクトル | string スカラー | 関数ハンドル

このプロパティは読み取り専用です。

インクリメンタル学習関数が生の応答値を変換する方法を記述するスコア変換関数。文字ベクトル、string スカラー、または関数ハンドルとして指定します。incrementalClassificationLinear は ScoreTransform 値を文字ベクトルまたは関数ハンドルとして格納します。

次の表は、スコア変換で使用可能な組み込み関数の一覧です。

値	説明
`"doublelogit"`	1/(1 + e^–2x)
`"invlogit"`	log(x / (1 – x))
`"ismax"`	最大のスコアをもつクラスのスコアを 1 に設定し、他のすべてのクラスのスコアを 0 に設定する
`"logit"`	1/(1 + e^–x)
`"none"` または `"identity"`	x (変換なし)
`"sign"`	x < 0 のとき –1 x = 0 のとき 0 x > 0 のとき 1
`"symmetric"`	2x – 1
`"symmetricismax"`	最大のスコアをもつクラスのスコアを 1 に設定し、他のすべてのクラスのスコアを –1 に設定する
`"symmetriclogit"`	2/(1 + e^–x) – 1

MATLAB^® 関数やユーザー定義関数の場合は、関数ハンドルを入力します。たとえば、'ScoreTransform',@function では次のようになります。

function は n 行 2 列の行列 (元のスコア) を受け入れ、同じサイズの行列 (変換されたスコア) を返します。列の順序は ClassNames プロパティのクラスの順序に対応します。
n は観測値の数であり、行列の行 j には、観測値 j のクラススコアが格納されます。

ScoreTransform の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルを変換して Mdl を作成する場合、ScoreTransform は従来式の学習済みモデルの対応するプロパティによって指定されます。たとえば、従来式の学習済みモデルの ScoreTransform プロパティがスコアから事後確率への変換関数である場合、fitPosterior または fitSVMPosterior によって計算されるものとして、Mdl.ScoreTransform は無名関数を含みます。
それ以外の場合、既定値は 'none' (Learner が 'svm' の場合) または 'logit' (Learner が 'logistic' の場合) です。

データ型: char | string | function_handle

学習パラメーター

`EstimationPeriod` — ハイパーパラメーターの推定のために処理する観測値の数
読み取り専用: 非負の整数

このプロパティは読み取り専用です。

ハイパーパラメーターの推定のために、パフォーマンスメトリクスの学習または追跡の前にインクリメンタルモデルが処理する観測値の数。非負の整数として指定します。

メモ

Mdl をインクリメンタル学習用に準備する場合 (学習に必要なすべてのハイパーパラメーターを指定する必要があります)、incrementalClassificationLinear は EstimationPeriod を 0 に強制します。
Mdl をインクリメンタル学習用に準備しない場合、incrementalClassificationLinear は EstimationPeriod を 1000 に設定します。

詳細は、推定期間を参照してください。

データ型: single | double

`FitBias` — 線形モデルの切片使用フラグ
読み取り専用: `true` | `false`

このプロパティは読み取り専用です。

線形モデルの切片使用フラグ。true または false として指定します。

値	説明
`true`	`incrementalClassificationLinear` は、バイアス項 β₀ を、インクリメンタル近似関数がデータに当てはめる線形モデルに含めます。
`false`	`incrementalClassificationLinear` は β₀ = 0 に設定します。

Bias ≠ 0 の場合、FitBias は true でなければなりません。つまり、incrementalClassificationLinear は β₀ の等式制約をサポートしません。

FitBias の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済み線形分類モデルオブジェクト (ClassificationLinear) を変換して Mdl を作成する場合、FitBias は従来式の学習済みモデルの ModelParameters プロパティの FitBias 値によって指定されます。
線形モデルテンプレートオブジェクト (templateLinear から返されるオブジェクト) を変換して Mdl を作成する場合、FitBias はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、既定値は true です。

データ型: logical

`Mu` — 予測子の平均
読み取り専用: 数値ベクトル | `[]`

このプロパティは読み取り専用です。

予測子の平均。数値ベクトルを指定します。

Mu が空の配列 [] で、'Standardize',true が指定されている場合、インクリメンタル近似関数は、Mu を EstimationPeriod で指定された推定期間中に推定された予測子変数の平均に設定します。

Mu を直接指定することはできません。

データ型: single | double

`Sigma` — 予測子の標準偏差
読み取り専用: 数値ベクトル | `[]`

このプロパティは読み取り専用です。

予測子の標準偏差。数値ベクトルを指定します。

Sigma が空の配列 [] で、'Standardize',true が指定されている場合、インクリメンタル近似関数は、Sigma を EstimationPeriod で指定された推定期間中に推定された予測子変数の標準偏差に設定します。

Sigma を直接指定することはできません。

データ型: single | double

`Solver` — 目的関数の最小化手法
読み取り専用: `'scale-invariant'` | `'sgd'` | `'asgd'`

このプロパティは読み取り専用です。

目的関数の最小化手法。'scale-invariant'、'sgd' または 'asgd' を指定します。incrementalClassificationLinear は Solver 値を文字ベクトルとして格納します。

値説明メモ:

値	説明	メモ:
`'scale-invariant'`	インクリメンタル学習用の適応型スケール不変ソルバー [1]	このアルゴリズムはパラメーターを持たず、予測子のスケールの違いに適応できます。SGD または ASGD を使用する前に、このアルゴリズムを試してください。関数 `fit` でモデルを当てはめる前にデータの入力チャンクをシャッフルするには、`Shuffle` を `true` に設定します。
`'sgd'`	確率的勾配降下法 (SGD) [3][2]	SGD で効果的に学習させるには、データを標準化し、SGD および ASGD ソルバーのパラメーターにリストされているオプションを使用してハイパーパラメーターの適切な値を指定します。関数 `fit` でモデルを当てはめる前にデータの入力チャンクが常にシャッフルされます。
`'asgd'`	平均化確率的勾配降下法 (ASGD) [4]	ASGD で効果的に学習させるには、データを標準化し、SGD および ASGD ソルバーのパラメーターにリストされているオプションを使用してハイパーパラメーターの適切な値を指定します。関数 `fit` でモデルを当てはめる前にデータの入力チャンクが常にシャッフルされます。

'scale-invariant'

インクリメンタル学習用の適応型スケール不変ソルバー [1]

このアルゴリズムはパラメーターを持たず、予測子のスケールの違いに適応できます。SGD または ASGD を使用する前に、このアルゴリズムを試してください。
関数 fit でモデルを当てはめる前にデータの入力チャンクをシャッフルするには、Shuffle を true に設定します。

'sgd'

確率的勾配降下法 (SGD) [3][2]

SGD で効果的に学習させるには、データを標準化し、SGD および ASGD ソルバーのパラメーターにリストされているオプションを使用してハイパーパラメーターの適切な値を指定します。
関数 fit でモデルを当てはめる前にデータの入力チャンクが常にシャッフルされます。

'asgd'

平均化確率的勾配降下法 (ASGD) [4]

ASGD で効果的に学習させるには、データを標準化し、SGD および ASGD ソルバーのパラメーターにリストされているオプションを使用してハイパーパラメーターの適切な値を指定します。
関数 fit でモデルを当てはめる前にデータの入力チャンクが常にシャッフルされます。

Solver の既定値は、モデルの作成方法に応じて異なります。

incrementalClassificationLinear を直接呼び出して Mdl を作成する場合、既定値は 'scale-invariant' です。
従来式の学習済み線形分類モデルオブジェクト (ClassificationLinear) または線形モデルテンプレートオブジェクト (templateLinear から返されるオブジェクト) を変換して Mdl を作成する場合、そのオブジェクトでリッジ正則化と SGD または ASGD ソルバーが使用されていると、Mdl は同じソルバーを使用します。
(従来式の学習済みモデル (たとえば TTMdl) の Solver の値は TTMdl.ModelParameters.Solver で確認できます。モデルテンプレートオブジェクトについては、コマンドウィンドウまたは変数エディターでオブジェクトを表示して Solver の値を確認できます。)
それ以外の場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 Solver で行います。この引数の既定値は 'scale-invariant' です。

データ型: char | string

`SolverOptions` — 目的ソルバーの構成
読み取り専用: 構造体配列

このプロパティは読み取り専用です。

目的ソルバーの構成。構造体配列として指定します。SolverOptions のフィールドは、指定したソルバー Solver 固有のプロパティです。

データ型: struct

SGD および ASGD ソルバーのパラメーター

`BatchSize` — ミニバッチのサイズ
読み取り専用: 正の整数

このプロパティは読み取り専用です。

ミニバッチのサイズ。正の整数として指定します。学習中の各学習サイクルで、incrementalClassificationLinear は BatchSize 個の観測値を使用して劣勾配を計算します。

最後のミニバッチ (fit または updateMetricsAndFit の各関数呼び出しにおける最後の学習サイクル) に使用する観測値の数は、BatchSize より小さくてもかまいません。たとえば、fit または updateMetricsAndFit に 25 個の観測値を指定した場合、関数は最初の 2 つの学習サイクルに 10 個の観測値を使用し、最後の学習サイクルに 5 の観測値を使用します。

BatchSize の既定値は、モデルの作成方法に応じて異なります。

incrementalClassificationLinear を直接呼び出して Mdl を作成する場合、既定値は 10 です。
従来式の学習済み線形分類モデルオブジェクト (ClassificationLinear) を変換して Mdl を作成する場合、そのオブジェクトでリッジ正則化と SGD または ASGD ソルバーが使用されていると、BatchSize は従来式の学習済みモデルの ModelParameters プロパティの BatchSize 値によって指定されます。
線形モデルテンプレートオブジェクト (templateLinear から返されるオブジェクト) を変換して Mdl を作成する場合、そのオブジェクトでリッジ正則化と SGD または ASGD ソルバーが使用されていると、BatchSize はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 BatchSize で行います。この引数の既定値は 10 です。

データ型: single | double

`Lambda` — リッジ (L2) 正則化項の強度
読み取り専用: 非負のスカラー

このプロパティは読み取り専用です。

リッジ (L2) 正則化項の強度。非負のスカラーとして指定します。

Lambda の既定値は、モデルの作成方法に応じて異なります。

incrementalClassificationLinear を直接呼び出して Mdl を作成する場合、既定値は 1e-5 です。
従来式の学習済み線形分類モデルオブジェクト (ClassificationLinear) または線形モデルテンプレートオブジェクト (templateLinear から返されるオブジェクト) を変換して Mdl を作成する場合、そのオブジェクトでリッジ正則化と SGD または ASGD ソルバーが使用されていると、Lambda はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 Lambda で行います。この引数の既定値は 1e-5 です。

データ型: double | single

`LearnRate` — 初期学習率
読み取り専用: `'auto'` | 正のスカラー

このプロパティは読み取り専用です。

初期学習率。'auto' または正のスカラーとして指定します。incrementalClassificationLinear は LearnRate 値を数値スカラーとして格納します。

学習率は、目的の劣勾配をスケールすることによって最適化のステップサイズを制御します。LearnRate は学習率の初期値を指定し、LearnRateSchedule によって後続の学習サイクルの学習率が決まります。

'auto' を指定した場合、次のようになります。

初期学習率は 0.7 となります。
EstimationPeriod > 0 の場合、fit および updateMetricsAndFit は、EstimationPeriod の最後にこの比率を 1/sqrt(1+max(sum(X.^2,obsDim))) に変更します。obsDim の値は、観測値が推定期間に収集された予測子データ X の列である場合は 1、それ以外の場合は 2 です。

LearnRate の既定値は、モデルの作成方法に応じて異なります。

incrementalClassificationLinear を直接呼び出して Mdl を作成する場合、既定値は 'auto' です。
従来式の学習済み線形分類モデルオブジェクト (ClassificationLinear) を変換して Mdl を作成する場合、そのオブジェクトでリッジ正則化と SGD または ASGD ソルバーが使用されていると、LearnRate は従来式の学習済みモデルの ModelParameters プロパティの LearnRate 値によって指定されます。
線形モデルテンプレートオブジェクト (templateLinear から返されるオブジェクト) を変換して Mdl を作成する場合、そのオブジェクトでリッジ正則化と SGD または ASGD ソルバーが使用されていると、LearnRate はオブジェクトの対応するプロパティによって指定されます。
それ以外の場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 LearnRate で行います。この引数の既定値は 'auto' です。

データ型: single | double | char | string

`LearnRateSchedule` — 学習率スケジュール
読み取り専用: `'decaying'` | `'constant'`

このプロパティは読み取り専用です。

学習率スケジュール。'decaying' または 'constant' として指定します。ここで、LearnRate は初期学習率 ɣ₀ を指定します。incrementalClassificationLinear は LearnRateSchedule 値を文字ベクトルとして格納します。

値説明

'constant' すべての学習サイクルの学習率を ɣ₀ とする。

値	説明
`'constant'`	すべての学習サイクルの学習率を ɣ₀ とする。
`'decaying'`	学習サイクル t での学習率を次とする。 $γ_{t} = \frac{γ_{0}}{{(1 + λ γ_{0} t)}^{c}} .$ λ は `Lambda` の値です。 `Solver` が `'sgd'` の場合、c = 1 です。 `Solver` が `'asgd'` の場合、c は 0.75 です[4]。

'decaying'

学習サイクル t での学習率を次とする。

$γ_{t} = \frac{γ_{0}}{{(1 + λ γ_{0} t)}^{c}} .$

λ は Lambda の値です。
Solver が 'sgd' の場合、c = 1 です。
Solver が 'asgd' の場合、c は 0.75 です[4]。

LearnRateSchedule の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルオブジェクトまたはテンプレートモデルオブジェクトを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 LearnRateSchedule で行います。この引数の既定値は 'decaying' です。
それ以外の場合、既定値は 'decaying' です。

データ型: char | string

パフォーマンスメトリクスパラメーター

`IsWarm` — モデルがパフォーマンスメトリクスを追跡するかどうかを示すフラグ
読み取り専用: `false` または `0` | `true` または `1`

このプロパティは読み取り専用です。

インクリメンタルモデルがパフォーマンスメトリクスを追跡するかどうかを示すフラグ。logical 0 (false) または 1 (true) として指定します。

インクリメンタルモデル Mdl は、インクリメンタル近似関数が (EstimationPeriod + MetricsWarmupPeriod) 個の観測値をインクリメンタルモデルに当てはめた後、"ウォーム" (IsWarm が true となる) になります。

値	説明
`true` または `1`	インクリメンタルモデル `Mdl` がウォームです。この結果、`updateMetrics` および `updateMetricsAndFit` が `Mdl` の `Metrics` プロパティのパフォーマンスメトリクスを追跡します。
`false` または `0`	`updateMetrics` および `updateMetricsAndFit` はパフォーマンスメトリクスを追跡しません。

データ型: logical

`Metrics` — モデルのパフォーマンスメトリクス
読み取り専用: table

このプロパティは読み取り専用です。

updateMetrics および updateMetricsAndFit によってインクリメンタル学習中に更新されたモデルのパフォーマンスメトリクス。m 行 2 列の table として指定します。ここで、m は、名前と値の引数 Metrics によって指定されたメトリクスの数です。

Metrics の列には Cumulative および Window のラベルが付けられます。

Cumulative:要素 j は、メトリクス j で測定される、モデルがウォーム (IsWarm が 1) になった時点からの、モデルの性能です。
Window:要素 j は、メトリクス j で測定され、MetricsWindowSize プロパティで指定されたウィンドウ内のすべての観測値に対して評価される、モデルの性能です。ソフトウェアは MetricsWindowSize 個の観測値を処理した後、Window を更新します。

行には、指定したメトリクスのラベルが付けられます。詳細については、incrementalLearner または incrementalClassificationLinear の名前と値の引数 Metrics を参照してください。

データ型: table

`MetricsWarmupPeriod` — パフォーマンスメトリクスを追跡する前に当てはめる観測値の数
読み取り専用: 非負の整数

このプロパティは読み取り専用です。

インクリメンタルモデルが Metrics プロパティのパフォーマンスメトリクスを追跡する前に当てはめなければならない観測値の数。非負の整数として指定します。

MetricsWarmupPeriod の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 MetricsWarmupPeriod で行います。この引数の既定値は 0 です。
それ以外の場合、既定値は 1000 です。

詳細については、パフォーマンスメトリクスを参照してください。

データ型: single | double

`MetricsWindowSize` — ウィンドウパフォーマンスメトリクスの計算に使用する観測値の数
読み取り専用: 正の整数

このプロパティは読み取り専用です。

ウィンドウパフォーマンスメトリクスの計算に使用する観測値の数。正の整数として指定します。

MetricsWindowSize の既定値は、モデルの作成方法に応じて異なります。

従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 MetricsWindowSize で行います。この引数の既定値は 200 です。
それ以外の場合、既定値は 200 です。

パフォーマンスメトリクスオプションの詳細については、パフォーマンスメトリクスを参照してください。

データ型: single | double

オブジェクト関数

`fit`	インクリメンタル学習用の線形モデルの学習
`updateMetricsAndFit`	線形インクリメンタル学習モデルの新しいデータに基づくパフォーマンスメトリクスの更新とモデルの学習
`updateMetrics`	線形インクリメンタル学習モデルの新しいデータに基づくパフォーマンスメトリクスの更新
`loss`	データのバッチでの線形インクリメンタル学習モデルの損失
`predict`	線形インクリメンタル学習モデルからの新しい観測の応答予測
`perObservationLoss`	インクリメンタル学習用モデルの観測値ごとの分類誤差
`reset`	インクリメンタル分類モデルのリセット

例

すべて折りたたむ

事前情報なしでのインクリメンタル学習器の作成

ライブスクリプトを開く

バイナリ分類用の既定のインクリメンタル線形 SVM モデルを作成します。

Mdl = incrementalClassificationLinear()

Mdl = 
  incrementalClassificationLinear

            IsWarm: 0
           Metrics: [1×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'none'
              Beta: [0×1 double]
              Bias: 0
           Learner: 'svm'


  Properties, Methods

Mdl は incrementalClassificationLinear モデルオブジェクトです。そのプロパティはすべて読み取り専用です。

Mdl は、他の演算の実行に使用する前に、データに当てはめなければなりません。

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

応答は、次の 5 つのクラスのいずれかになります。座る、立つ、歩く、走る、または踊る。被験者が移動しているかどうか (actid > 2) を基準に、応答を二分します。

Y = Y > 2;

関数 updateMetricsAndFit を使用して、インクリメンタルモデルを学習データに当てはめます。50 個の観測値のチャンクを一度に処理して、データストリームをシミュレートします。各反復で次を行います。

50 個の観測値を処理します。
前のインクリメンタルモデルを、入力観測値に当てはめた新しいモデルで上書きします。
$β_{1}$ 、累積メトリクス、およびウィンドウメトリクスを保存し、インクリメンタル学習中にそれらがどのように進化するかを確認。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta1 = zeros(nchunk+1,1);    

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,X(idx,:),Y(idx));
    ce{j,:} = Mdl.Metrics{"ClassificationError",:};
    beta1(j + 1) = Mdl.Beta(1);
end

IncrementalMdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationLinear モデルオブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetricsAndFit は入力観測値でモデルの性能をチェックし、モデルをその観測値に当てはめます。

パフォーマンスメトリクスと $β_{1}$ が学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(beta1)
ylabel('\beta_1')
xlim([0 nchunk])
nexttile
h = plot(ce.Variables);
xlim([0 nchunk])
ylabel('Classification Error')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
legend(h,ce.Properties.VariableNames)
xlabel(t,'Iteration')

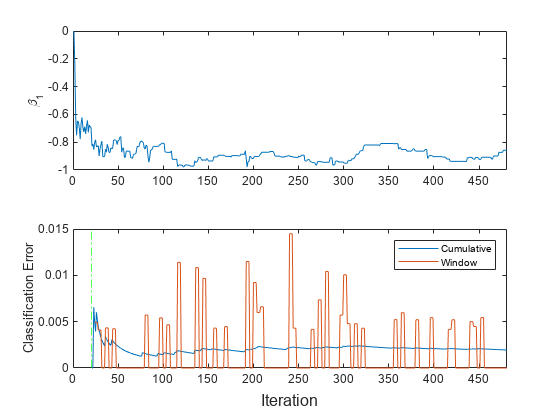
$Figure contains 2 axes objects. Axes object 1 with ylabel \beta_1 contains an object of type line. Axes object 2 with ylabel Classification Error contains 3 objects of type line, constantline. These objects represent Cumulative, Window.$

プロットは、updateMetricsAndFit が次を行うことを示しています。

$β_{1}$ をインクリメンタル学習のすべての反復で当てはめます。
パフォーマンスメトリクスをメトリクスのウォームアップ期間後にのみ計算します。
累積メトリクスを各反復中に計算します。
ウィンドウメトリクスを 200 個の観測値 (4 回の反復) の処理後に計算します。

インクリメンタル学習オプションの構成

ライブスクリプトを開く

メトリクスのウォームアップ期間を指定して、インクリメンタルバイナリ SVM 学習器を準備します。その間、関数 updateMetricsAndFit はモデルの当てはめのみを行います。メトリクスウィンドウサイズを観測値 500 個に指定します。SGD を使用してモデルに学習させ、SGD バッチサイズ、学習率、および正則化パラメーターを調整します。

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng("default") % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

Y = Y > 2;

バイナリ分類用のインクリメンタル線形モデルを作成します。次のようにモデルを構成します。

インクリメンタル近似関数で生の (標準化されていない) 予測子データを処理するように指定します。
SGD ソルバーを指定します。
リッジ正則化パラメーター値 0.001、SGD バッチサイズ 20、および学習率 0.002 で、問題に対して十分に機能すると仮定します。
メトリクスのウォームアップ期間を観測値 5000 個に指定します。
メトリクスウィンドウサイズを観測値 500 個に指定します。
分類およびヒンジエラーメトリクスを追跡して、モデルの性能を測定します。

Mdl = incrementalClassificationLinear('Standardize',false, ...
    'Solver','sgd','Lambda',0.001,'BatchSize',20,'LearnRate',0.002, ...
    'MetricsWarmupPeriod',5000,'MetricsWindowSize',500, ...
    'Metrics',{'classiferror' 'hinge'})

Mdl = 
  incrementalClassificationLinear

            IsWarm: 0
           Metrics: [2×2 table]
        ClassNames: [1×0 double]
    ScoreTransform: 'none'
              Beta: [0×1 double]
              Bias: 0
           Learner: 'svm'


  Properties, Methods

Mdl はインクリメンタル学習用に構成された incrementalClassificationLinear モデルオブジェクトです。

関数 updateMetricsAndFit を使用して、インクリメンタルモデルを残りのデータに当てはめます。各反復で次を行います。

50 個の観測値のチャンクを処理して、データストリームをシミュレートします。チャンクのサイズと SGD バッチサイズは異なることに注意してください。
前のインクリメンタルモデルを、入力観測値に当てはめた新しいモデルで上書きします。
推定係数 $β_{10}$ 、累積メトリクス、およびウィンドウメトリクスを保存し、インクリメンタル学習中にそれらがどのように進化するかを確認します。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
hinge = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta10 = zeros(nchunk+1,1);    

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,X(idx,:),Y(idx));
    ce{j,:} = Mdl.Metrics{"ClassificationError",:};
    hinge{j,:} = Mdl.Metrics{"HingeLoss",:};
    beta10(j + 1) = Mdl.Beta(10);
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationLinear モデルオブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetricsAndFit は入力観測値でモデルの性能をチェックし、モデルをその観測値に当てはめます。

パフォーマンスメトリクスと $β_{10}$ が学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

tiledlayout(2,2)
nexttile
plot(beta10)
ylabel('\beta_{10}')
xlim([0 nchunk]);
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
xlabel('Iteration')
nexttile
h = plot(ce.Variables);
xlim([0 nchunk]);
ylabel('Classification Error')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
legend(h,ce.Properties.VariableNames)
xlabel('Iteration')
nexttile
h = plot(hinge.Variables);
xlim([0 nchunk]);
ylabel('Hinge Loss')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'g-.')
legend(h,hinge.Properties.VariableNames)
xlabel('Iteration')

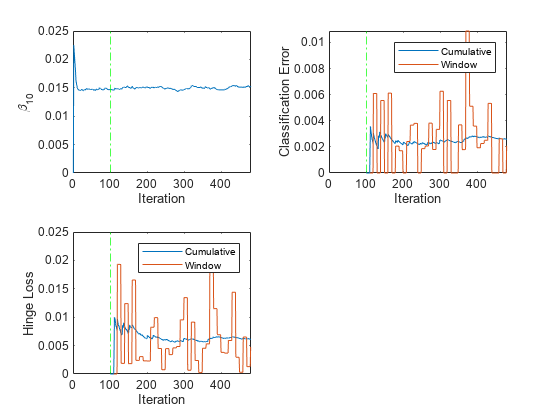
$Figure contains 3 axes objects. Axes object 1 with xlabel Iteration, ylabel \beta_{10} contains 2 objects of type line, constantline. Axes object 2 with xlabel Iteration, ylabel Classification Error contains 3 objects of type line, constantline. These objects represent Cumulative, Window. Axes object 3 with xlabel Iteration, ylabel Hinge Loss contains 3 objects of type line, constantline. These objects represent Cumulative, Window.$

プロットは、updateMetricsAndFit が次を行うことを示しています。

$β_{10}$ をインクリメンタル学習のすべての反復で当てはめます。
パフォーマンスメトリクスをメトリクスのウォームアップ期間後にのみ計算します。
累積メトリクスを各反復中に計算します。
ウィンドウメトリクスを 500 個の観測値 (10 回の反復) の処理後に計算します。

従来式の学習済みモデルのインクリメンタル学習器への変換

ライブスクリプトを開く

fitclinear を使用してバイナリ分類用の線形モデルに学習させ、それをインクリメンタル学習器に変換し、その性能を追跡し、ストリーミングデータに当てはめます。学習オプションを従来式からインクリメンタル学習に引き継ぎます。

データの読み込みと前処理

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。予測子データの観測値を列に配置します。

load humanactivity
rng(1); % For reproducibility
n = numel(actid);
idx = randsample(n,n);
X = feat(idx,:)';
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

Y = Y > 2;

被験者がアイドル (Y = false) だったときの収集データが、被験者が移動していたときのデータの倍の品質であると仮定します。アイドルの被験者から収集した観測値に 2 を割り当て、移動している被験者から収集した観測値に 1 を割り当てる重み変数を作成します。

W = ones(n,1) + ~Y;

バイナリ分類用の線形モデルの学習

バイナリ分類用の線形モデルを、データの半分から取った無作為標本に当てはめます。

idxtt = randsample([true false],n,true);
TTMdl = fitclinear(X(:,idxtt),Y(idxtt),'ObservationsIn','columns', ...
    'Weights',W(idxtt))

TTMdl = 
  ClassificationLinear
      ResponseName: 'Y'
        ClassNames: [0 1]
    ScoreTransform: 'none'
              Beta: [60×1 double]
              Bias: -0.1107
            Lambda: 8.2967e-05
           Learner: 'svm'


  Properties, Methods

TTMdl は、バイナリ分類用の従来式の学習済み線形モデルを表す ClassificationLinear モデルオブジェクトです。

学習済みモデルの変換

従来式の学習済み分類モデルを、インクリメンタル学習用のバイナリ分類線形モデルに変換します。

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalClassificationLinear

            IsWarm: 1
           Metrics: [1×2 table]
        ClassNames: [0 1]
    ScoreTransform: 'none'
              Beta: [60×1 double]
              Bias: -0.1107
           Learner: 'svm'


  Properties, Methods

パフォーマンスメトリクスの追跡とモデルの当てはめの個別の実行

関数 updateMetrics および fit を使用して、残りのデータに対してインクリメンタル学習を実行します。50 個の観測値を一度に処理して、データストリームをシミュレートします。各反復で次を行います。

updateMetrics を呼び出し、観測値の入力チャンクを所与として、モデルの分類誤差の累積とウィンドウを更新します。前のインクリメンタルモデルを上書きして、Metrics プロパティ内の損失を更新します。関数がモデルをデータチャンクに当てはめないことに注意してください。チャンクはモデルに対して "新しい" データです。観測値の向きを列方向に指定し、観測値の重みを指定します。
fit を呼び出して、観測値の入力チャンクにモデルを当てはめます。前のインクリメンタルモデルを上書きして、モデルパラメーターを更新します。観測値の向きを列方向に指定し、観測値の重みを指定します。
分類誤差と推定された最初の係数 $β_{1}$ を保存します。

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 50;
nchunk = floor(nil/numObsPerChunk);
ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta1 = [IncrementalMdl.Beta(1); zeros(nchunk,1)];
Xil = X(:,idxil);
Yil = Y(idxil);
Wil = W(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(:,idx),Yil(idx), ...
        'ObservationsIn','columns','Weights',Wil(idx));
    ce{j,:} = IncrementalMdl.Metrics{"ClassificationError",:};
    IncrementalMdl = fit(IncrementalMdl,Xil(:,idx),Yil(idx), ...
        'ObservationsIn','columns','Weights',Wil(idx));
    beta1(j + 1) = IncrementalMdl.Beta(end);
end

IncrementalMdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationLinear モデルオブジェクトです。

あるいは、updateMetricsAndFit を使用して、新しいデータチャンクに対するモデルのパフォーマンスメトリクスを更新し、モデルをデータに当てはめることもできます。

パフォーマンスメトリクスと推定された係数 $β_{1}$ のトレースプロットをプロットします。

t = tiledlayout(2,1);
nexttile
h = plot(ce.Variables);
xlim([0 nchunk])
ylabel('Classification Error')
legend(h,ce.Properties.VariableNames)
nexttile
plot(beta1)
ylabel('\beta_1')
xlim([0 nchunk])
xlabel(t,'Iteration')

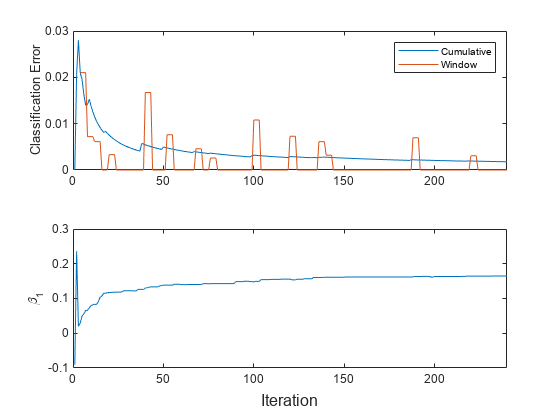
$Figure contains 2 axes objects. Axes object 1 with ylabel Classification Error contains 2 objects of type line. These objects represent Cumulative, Window. Axes object 2 with ylabel \beta_1 contains an object of type line.$

累積の損失は安定しており徐々に減少しますが、ウィンドウの損失には急な変動があります。

$β_{1}$ はまず急激に変動した後、fit がより多くのチャンクを処理するにつれて徐々に平坦になります。

詳細

すべて展開する

インクリメンタル学習

"インクリメンタル学習" ("オンライン学習") は、予測子変数の分布、予測関数や目的関数の素性 (調整パラメーターの値を含む)、観測値にラベル付けがされているか等についてほぼ知識が無い時に、データストリームから入ってくるデータを処理することに関係している機械学習の一分野です。従来の機械学習は、モデルへの当てはめに十分にラベル付けされたデータを使用でき、交差検証を実施してハイパーパラメーターを調整し、予測子の分布を推論するもので、インクリメンタル学習と異なります。

入力観測値に対し、インクリメンタル学習モデルは、次のいずれかの方法 (通常はこの順序) でデータを処理します。

ラベルを予測します。
予測性能を測定します。
モデルの構造的な破綻やドリフトについてチェックします。
入力観測値へモデルを当てはめます。

詳細については、インクリメンタル学習の概要を参照してください。

インクリメンタル学習用の適応型スケール不変ソルバー

"インクリメンタル学習用の適応型スケール不変ソルバー" ([1]で紹介) は、線形予測モデルに学習させるための勾配降下法ベースの目的ソルバーです。ソルバーはハイパーパラメーターを持たず、予測子変数のスケールの違いの影響を受けず、予測子変数の分布の事前知識が不要です。これらの特徴は、インクリメンタル学習に適しています。

標準 SGD および ASGD ソルバーは、予測子変数間のスケールの違いの影響を受けやすいため、モデルの性能低下につながることがあります。SGD および ASGD を使用して精度を向上させるには、予測子データを標準化し、正則化と学習率のパラメーターを調整できます。従来の機械学習では、交差検証と予測子を標準化してハイパーパラメーター調整を行うのに十分なデータが利用できます。しかし、インクリメンタル学習の場合、十分なデータが利用できず (たとえば、観測値が一度に 1 つしか利用できない場合があります)、予測子の分布が未知である場合があります。このような特徴があるため、インクリメンタル学習中のパラメーター調整と予測子の標準化は困難または不可能です。

分類用のインクリメンタル近似関数 fit および updateMetricsAndFit は、アルゴリズムのより積極的な ScInOL2 バージョンを使用します。

ヒント

モデルを作成した後で、データストリームについてインクリメンタル学習を実行する C/C++ コードを生成できます。C/C++ コードの生成には MATLAB Coder™ が必要です。詳細については、コード生成の紹介を参照してください。

アルゴリズム

すべて展開する

推定期間

推定期間中、インクリメンタル近似関数 fit および updateMetricsAndFit は、最初の EstimationPeriod 個の入力観測値を使用して、インクリメンタル学習に必要なハイパーパラメーターを推定 (調整) します。推定は EstimationPeriod が正の場合にのみ発生します。次の表は、ハイパーパラメーターとそれらが推定または調整される条件について説明します。

ハイパーパラメーターモデルプロパティ使用法条件

予測子の平均および標準偏差

ハイパーパラメーター	モデルプロパティ	使用法	条件
予測子の平均および標準偏差	`Mu` および `Sigma`	標準化された予測子データ	次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。予測子データを標準化するようにインクリメンタル近似関数を構成 (データの標準化を参照)。 `Mdl.Mu` および `Mdl.Sigma` が空の配列 `[]`。
学習率	`LearnRate`	ソルバーのステップサイズの調整	次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。ソルバーが SGD または ASGD (`Solver` を参照)。名前と値の引数 `'LearnRate'` を正のスカラーとして指定していない。

Mu および Sigma

標準化された予測子データ

次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。

予測子データを標準化するようにインクリメンタル近似関数を構成 (データの標準化を参照)。
Mdl.Mu および Mdl.Sigma が空の配列 []。

学習率

LearnRate

ソルバーのステップサイズの調整

次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。

ソルバーが SGD または ASGD (Solver を参照)。
名前と値の引数 'LearnRate' を正のスカラーとして指定していない。

推定期間中には、fit がモデルを当てはめることも、updateMetricsAndFit がモデルを当てはめたりパフォーマンスメトリクスを更新したりすることもありません。推定期間の満了時に、関数はハイパーパラメーターを格納するプロパティを更新します。

データの標準化

予測子変数を標準化するようにインクリメンタル学習関数が構成されている場合、インクリメンタル学習モデル Mdl の Mu および Sigma プロパティに保存されている平均と標準偏差を使用して標準化が行われます。

'Standardize',true と正の推定期間 (EstimationPeriod を参照) が設定されていて、Mdl.Mu と Mdl.Sigma が空の場合、インクリメンタル近似関数は、推定期間の観測値を使用して平均と標準偏差を推定します。
'Standardize','auto' を設定すると (既定の設定)、次の条件が適用されます。
- 従来式の学習済みバイナリ線形 SVM モデル (ClassificationSVM または CompactClassificationSVM) を変換して incrementalClassificationLinear を作成する場合、従来式の学習済みモデルの Mu および Sigma プロパティが空の配列 [] であれば、インクリメンタル学習関数は予測子変数を標準化しません。従来式の学習済みモデルの Mu および Sigma プロパティが空でない場合、インクリメンタル学習関数は、指定された平均と標準偏差を使用して予測子変数を標準化します。インクリメンタル近似関数は、推定期間の長さにかかわらず、新しい平均と標準偏差を推定しません。
- 線形分類モデル (ClassificationLinear) を変換して incrementalClassificationLinear を作成する場合、インクリメンタル学習関数は、推定期間の長さにかかわらず、データを標準化しません。
- 従来式の学習済みモデルを変換するのでない場合、インクリメンタル学習関数は、SGD ソルバー (Solver を参照) と正の推定期間 (EstimationPeriod を参照) が指定されている場合にのみ予測子データを標準化します。
インクリメンタル近似関数が予測子の平均と標準偏差を推定するとき、関数は推定期間の観測値を使用して加重平均と加重標準偏差を計算します。具体的には、関数は予測子 j (x_j) の標準化のために次を使用します。

$x_{j}^{*} = \frac{x_{j} - μ_{j}^{*}}{σ_{j}^{*}} .$
- x_j は予測子 j、x_jk は推定期間内の予測子 j の観測値 k です。
- $μ_{j}^{*} = \frac{1}{\sum_{k} w_{k}^{*}} \sum_{k} w_{k}^{*} x_{j k} .$
- ${(σ_{j}^{*})}^{2} = \frac{1}{\sum_{k} w_{k}^{*}} \sum_{k} w_{k}^{*} {(x_{j k} - μ_{j}^{*})}^{2} .$
- $w_{j}^{*} = \frac{w_{j}}{\sum_{\forall j \in Class k} w_{j}} p_{k},$
  - p_k はクラス k の事前確率です (インクリメンタルモデルの Prior プロパティ)。
  - w_j は観測値の重み j です。

パフォーマンスメトリクス

関数 updateMetrics および updateMetricsAndFit は、インクリメンタルモデルが "ウォーム" (IsWarm プロパティ) のときに、新しいデータからモデルのパフォーマンスメトリクス ('Metrics') を追跡します。インクリメンタルモデルは、fit または updateMetricsAndFit がインクリメンタルモデルを MetricsWarmupPeriod 個の観測値 ("メトリクスのウォームアップ期間") に当てはめた後、ウォームになります。
EstimationPeriod > 0 の場合、関数はモデルをデータに当てはめる前にハイパーパラメーターを推定します。そのため、関数は、モデルがメトリクスのウォームアップ期間を開始する前に EstimationPeriod 個の観測値を追加で処理しなければなりません。
インクリメンタルモデルの Metrics プロパティは、各パフォーマンスメトリクスの 2 つの形式を table の変数 (列) Cumulative および Window とし、個々のメトリクスを行に格納します。インクリメンタルモデルがウォームになると、updateMetrics および updateMetricsAndFit は次の頻度でメトリクスを更新します。
- Cumulative — 関数は、モデルの性能追跡の開始以降の累積メトリクスを計算します。関数は、関数が呼び出されるたびにメトリクスを更新し、提供されたデータセット全体に基づいて計算を行います。
- Window — 関数は、名前と値のペアの引数 MetricsWindowSize によって決定されたウィンドウ内のすべての観測値に基づいてメトリクスを計算します。MetricsWindowSize によってソフトウェアが Window メトリクスを更新する頻度も決まります。たとえば、MetricsWindowSize が 20 の場合、関数は提供されたデータの最後の 20 個の観測値に基づいてメトリクスを計算します (X((end – 20 + 1):end,:) および Y((end – 20 + 1):end))。
  ウィンドウ内のパフォーマンスメトリクスを追跡するインクリメンタル関数は、次のプロセスを使用します。
  1. 指定された各メトリクスについて長さ MetricsWindowSize のバッファーを保存し、観測値の重みのバッファーを保存します。
  2. 入力観測値のバッチに基づくモデル性能をメトリクスバッファーの要素に入力し、対応する観測値の重みを重みバッファーに格納します。
  3. バッファーがいっぱいになると、Mdl.Metrics.Window をメトリクスウィンドウの性能の加重平均で上書きします。関数が観測値のバッチを処理するときにバッファーがあふれる場合、最新の入力観測値 MetricsWindowSize がバッファーに入り、最も古い観測値がバッファーから削除されます。たとえば、MetricsWindowSize が 20 で、メトリクスバッファーには前に処理されたバッチからの 10 個の値が存在し、15 個の値が入力されるとします。長さ 20 のウィンドウを構成するため、関数は 15 個の入力観測値からの測定値と前のバッチからの最新の 5 個の測定値を使用します。

Cumulative と Window のパフォーマンスメトリクスの値を計算する際、スコアが NaN の観測値は省略されます。

参照

[1] Kempka, Michał, Wojciech Kotłowski, and Manfred K. Warmuth. "Adaptive Scale-Invariant Online Algorithms for Learning Linear Models." Preprint, submitted February 10, 2019. https://arxiv.org/abs/1902.07528.

[2] Langford, J., L. Li, and T. Zhang. “Sparse Online Learning Via Truncated Gradient.” J. Mach. Learn. Res., Vol. 10, 2009, pp. 777–801.

[3] Shalev-Shwartz, S., Y. Singer, and N. Srebro. “Pegasos: Primal Estimated Sub-Gradient Solver for SVM.” Proceedings of the 24th International Conference on Machine Learning, ICML ’07, 2007, pp. 807–814.

[4] Xu, Wei. “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent.” CoRR, abs/1107.2490, 2011.

拡張機能

すべて展開する

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

incrementalClassificationLinear モデルオブジェクトのすべてのオブジェクト関数でコード生成がサポートされます。ただし、perObservationLoss と reset ではサポートされません。
データをシャッフルするように Mdl を構成した場合 (Solver および Shuffle を参照)、関数 fit は、モデルをバッチに当てはめる前に観測値の各入力バッチを無作為にシャッフルします。シャッフルされた観測値の順序は、MATLAB で生成される順序と一致しないことがあります。
incrementalClassificationLinear モデルオブジェクトを読み込むか作成するコードを生成する場合、次の制限が適用されます。
- 事後確率をスコアとして返すように構成された変換済み SVM モデルを Mdl で表現することはできません。
- 予測されるすべてのクラス名を ClassNames プロパティに含めなければなりません。
- 予測子変数の数を NumPredictors プロパティに反映しなければなりません。

詳細は、コード生成の紹介を参照してください。

バージョン履歴

R2020b で導入

参考

関数

fit | updateMetrics | updateMetricsAndFit | predict | incrementalLearner (ClassificationLinear) | incrementalLearner (ClassificationSVM)

オブジェクト

ClassificationLinear | ClassificationSVM | CompactClassificationSVM

incrementalClassificationLinear

説明

作成

構文

説明

名前と値の引数

Metrics — インクリメンタル学習中に追跡するモデルのパフォーマンス メトリクス "classiferror" (既定値) | string ベクトル | 関数ハンドル | cell ベクトル | 構造体配列 | "binodeviance" | "exponential" | "hinge" | "logit" | "quadratic"

Standardize — 予測子データを標準化するためのフラグ 'auto' (既定値) | false | true

Shuffle — 観測値のシャッフル フラグ true (既定値) | false

プロパティ

分類モデルのパラメーター

Beta — 線形モデル係数 β 読み取り専用: 数値ベクトル

Bias — モデル切片 β0 読み取り専用: 数値スカラー

ClassNames — 一意のクラス ラベル 読み取り専用: categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

FittedLoss — 線形モデルの当てはめに使用する損失関数 読み取り専用: 'hinge' | 'logit'

Learner — 線形分類モデルのタイプ 読み取り専用: 'svm' | 'logistic'

NumPredictors — 予測子変数の数 読み取り専用: 非負の数値スカラー

NumTrainingObservations — インクリメンタル モデルに当てはめる観測値の数 読み取り専用: 0 (既定値) | 非負の数値スカラー

Prior — 事前クラス確率 読み取り専用: 'empirical' | 'uniform' | 数値ベクトル

ScoreTransform — スコア変換関数 読み取り専用: 文字ベクトル | string スカラー | 関数ハンドル

学習パラメーター

EstimationPeriod — ハイパーパラメーターの推定のために処理する観測値の数 読み取り専用: 非負の整数

FitBias — 線形モデルの切片使用フラグ 読み取り専用: true | false

Mu — 予測子の平均 読み取り専用: 数値ベクトル | []

Sigma — 予測子の標準偏差 読み取り専用: 数値ベクトル | []

Solver — 目的関数の最小化手法 読み取り専用: 'scale-invariant' | 'sgd' | 'asgd'

SolverOptions — 目的ソルバーの構成 読み取り専用: 構造体配列

SGD および ASGD ソルバーのパラメーター

BatchSize — ミニバッチのサイズ 読み取り専用: 正の整数

Lambda — リッジ (L2) 正則化項の強度 読み取り専用: 非負のスカラー

LearnRate — 初期学習率 読み取り専用: 'auto' | 正のスカラー

LearnRateSchedule — 学習率スケジュール 読み取り専用: 'decaying' | 'constant'

パフォーマンス メトリクス パラメーター

IsWarm — モデルがパフォーマンス メトリクスを追跡するかどうかを示すフラグ 読み取り専用: false または 0 | true または 1

Metrics — モデルのパフォーマンス メトリクス 読み取り専用: table

MetricsWarmupPeriod — パフォーマンス メトリクスを追跡する前に当てはめる観測値の数 読み取り専用: 非負の整数

MetricsWindowSize — ウィンドウ パフォーマンス メトリクスの計算に使用する観測値の数 読み取り専用: 正の整数

オブジェクト関数

例

事前情報なしでのインクリメンタル学習器の作成

インクリメンタル学習オプションの構成

従来式の学習済みモデルのインクリメンタル学習器への変換

詳細

インクリメンタル学習

インクリメンタル学習用の適応型スケール不変ソルバー

ヒント

アルゴリズム

推定期間

データの標準化

パフォーマンス メトリクス

参照

拡張機能

C/C++ コード生成 MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

参考

関数

オブジェクト

トピック

`Metrics` — インクリメンタル学習中に追跡するモデルのパフォーマンスメトリクス
`"classiferror"` (既定値) | string ベクトル | 関数ハンドル | cell ベクトル | 構造体配列 | `"binodeviance"` | `"exponential"` | `"hinge"` | `"logit"` | `"quadratic"`

`Standardize` — 予測子データを標準化するためのフラグ
`'auto'` (既定値) | `false` | `true`

`Shuffle` — 観測値のシャッフルフラグ
`true` (既定値) | `false`

`Beta` — 線形モデル係数 β
読み取り専用: 数値ベクトル

`Bias` — モデル切片 β₀
読み取り専用: 数値スカラー

`ClassNames` — 一意のクラスラベル
読み取り専用: categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

`FittedLoss` — 線形モデルの当てはめに使用する損失関数
読み取り専用: `'hinge'` | `'logit'`

`Learner` — 線形分類モデルのタイプ
読み取り専用: `'svm'` | `'logistic'`

`NumPredictors` — 予測子変数の数
読み取り専用: 非負の数値スカラー

`NumTrainingObservations` — インクリメンタルモデルに当てはめる観測値の数
読み取り専用: `0` (既定値) | 非負の数値スカラー

`Prior` — 事前クラス確率
読み取り専用: `'empirical'` | `'uniform'` | 数値ベクトル

`ScoreTransform` — スコア変換関数
読み取り専用: 文字ベクトル | string スカラー | 関数ハンドル

`EstimationPeriod` — ハイパーパラメーターの推定のために処理する観測値の数
読み取り専用: 非負の整数

`FitBias` — 線形モデルの切片使用フラグ
読み取り専用: `true` | `false`

`Mu` — 予測子の平均
読み取り専用: 数値ベクトル | `[]`

`Sigma` — 予測子の標準偏差
読み取り専用: 数値ベクトル | `[]`

`Solver` — 目的関数の最小化手法
読み取り専用: `'scale-invariant'` | `'sgd'` | `'asgd'`

`SolverOptions` — 目的ソルバーの構成
読み取り専用: 構造体配列

`BatchSize` — ミニバッチのサイズ
読み取り専用: 正の整数

`Lambda` — リッジ (L2) 正則化項の強度
読み取り専用: 非負のスカラー

`LearnRate` — 初期学習率
読み取り専用: `'auto'` | 正のスカラー

`LearnRateSchedule` — 学習率スケジュール
読み取り専用: `'decaying'` | `'constant'`

パフォーマンスメトリクスパラメーター

`IsWarm` — モデルがパフォーマンスメトリクスを追跡するかどうかを示すフラグ
読み取り専用: `false` または `0` | `true` または `1`

`Metrics` — モデルのパフォーマンスメトリクス
読み取り専用: table

`MetricsWarmupPeriod` — パフォーマンスメトリクスを追跡する前に当てはめる観測値の数
読み取り専用: 非負の整数

`MetricsWindowSize` — ウィンドウパフォーマンスメトリクスの計算に使用する観測値の数
読み取り専用: 正の整数

パフォーマンスメトリクス

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。