updateMetrics

線形インクリメンタル学習モデルの新しいデータに基づくパフォーマンスメトリクスの更新

R2020b 以降

構文

Mdl = updateMetrics(Mdl,X,Y)

Mdl = updateMetrics(Mdl,X,Y,Name,Value)

説明

ストリーミングデータが与えられると、updateMetrics は、線形回帰用 (incrementalRegressionLinear オブジェクト) または線形バイナリ分類用 (incrementalClassificationLinear オブジェクト) に構成されたインクリメンタル学習モデルのパフォーマンスを測定します。updateMetrics はパフォーマンスメトリクスを出力モデルに格納します。

updateMetrics では柔軟なインクリメンタル学習が可能です。この関数を呼び出してデータの入力チャンクでモデルのパフォーマンスメトリクスを更新した後、モデルにデータを学習させる前に他のアクションを実行できます。たとえば、データのチャンクでのパフォーマンスに基づいて、モデルに学習させる必要があるかどうかを決定できます。また、関数 updateMetricsAndFit を使用すると、データが到達したときにモデルのパフォーマンスメトリクスの更新とモデルの学習の両方を 1 回の呼び出しで実行できます。

指定したデータのバッチにおけるモデルのパフォーマンスを測定するには、代わりに loss を呼び出します。

例

Mdl = updateMetrics(Mdl,X,Y) は、インクリメンタル学習モデル Mdl を返します。これは、入力予測子と応答データ (それぞれ X と Y) のモデルパフォーマンスメトリクスを含むように変更された入力インクリメンタル学習モデル Mdl です。

入力モデルが "ウォーム" (Mdl.IsWarm が true) の場合、updateMetrics は以前に計算されたメトリクスを上書きし、Metrics プロパティに新しい値を保存します。それ以外の場合、updateMetrics は代わりに Metrics に NaN 値を保存します。

入力モデルと出力モデルのデータ型は同じです。

例

Mdl = updateMetrics(Mdl,X,Y,Name,Value) は、1 つ以上の名前と値のペアの引数によって指定された追加オプションを使用します。たとえば、予測子データ行列の列が観測値に対応するように指定したり、観測値の重みを設定したりできます。

例

すべて折りたたむ

インクリメンタルモデルのパフォーマンスの追跡

ライブスクリプトを開く

fitclinear を使用してバイナリ分類用の線形モデルに学習させ、それをインクリメンタル学習器に変換し、そのパフォーマンスをストリーミングデータまで追跡します。

データの読み込みと前処理

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
rng(1) % For reproducibility
n = numel(actid);
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

応答は、次の 5 つのクラスのいずれかになります。座る、立つ、歩く、走る、または踊る。被験者が移動しているかどうか (actid > 2) を基準に、応答を二分します。

Y = Y > 2;

バイナリ分類用の線形モデルの学習

バイナリ分類用の線形モデルを、データの半分から取った無作為標本に当てはめます。

idxtt = randsample([true false],n,true);
TTMdl = fitclinear(X(idxtt,:),Y(idxtt))

TTMdl = 
  ClassificationLinear
      ResponseName: 'Y'
        ClassNames: [0 1]
    ScoreTransform: 'none'
              Beta: [60x1 double]
              Bias: -0.2999
            Lambda: 8.2967e-05
           Learner: 'svm'

TTMdl は、バイナリ分類用の従来式の学習済み線形モデルを表す ClassificationLinear モデルオブジェクトです。

学習済みモデルの変換

従来式の学習済み分類モデルを、インクリメンタル学習用のバイナリ分類線形モデルに変換します。

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalClassificationLinear

            IsWarm: 1
           Metrics: [1x2 table]
        ClassNames: [0 1]
    ScoreTransform: 'none'
              Beta: [60x1 double]
              Bias: -0.2999
           Learner: 'svm'

IncrementalMdl.IsWarm

ans = logical
   1

インクリメンタルモデルがウォームです。そのため、updateMetrics は、与えられたデータでのモデルのパフォーマンスメトリクスを追跡できます。

パフォーマンスメトリクスの追跡

関数 updateMetrics を使用して、残りのデータでのモデルパフォーマンスを追跡します。50 個の観測値を一度に処理して、データストリームをシミュレートします。各反復で次を行います。

updateMetrics を呼び出し、観測値の入力チャンクを所与として、モデルの分類誤差の累積とウィンドウを更新します。前のインクリメンタルモデルを上書きして、Metrics プロパティ内の損失を更新します。関数がモデルをデータチャンクに当てはめないことに注意してください。チャンクはモデルに対して "新しい" データです。
分類誤差と最初の係数 $β_{1}$ を保存します。

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 50;
nchunk = floor(nil/numObsPerChunk);
ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta1 = [IncrementalMdl.Beta(1); zeros(nchunk,1)];
Xil = X(idxil,:);
Yil = Y(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx));
    ce{j,:} = IncrementalMdl.Metrics{"ClassificationError",:};
    beta1(j + 1) = IncrementalMdl.Beta(1);
end

IncrementalMdl は、モデルパフォーマンスをデータストリーム内の観測値まで追跡した incrementalClassificationLinear モデルオブジェクトです。

パフォーマンスメトリクスと推定された係数 $β_{1}$ のトレースプロットをプロットします。

t = tiledlayout(2,1);
nexttile
h = plot(ce.Variables);
xlim([0 nchunk])
ylabel('Classification Error')
legend(h,ce.Properties.VariableNames)
nexttile
plot(beta1)
ylabel('\beta_1')
xlim([0 nchunk])
xlabel(t,'Iteration')

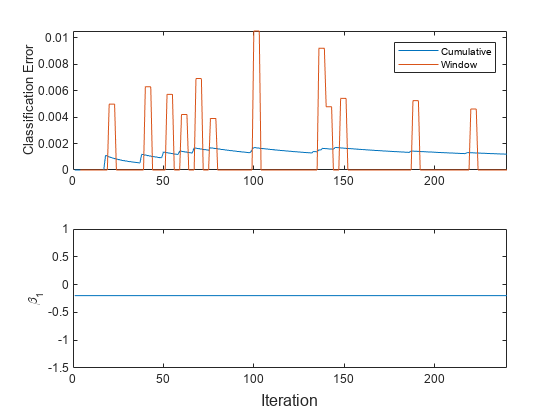
$Figure contains 2 axes objects. Axes object 1 with ylabel Classification Error contains 2 objects of type line. These objects represent Cumulative, Window. Axes object 2 with ylabel \beta_1 contains an object of type line.$

累積の損失は安定していますが、ウィンドウの損失には急な変動があります。

updateMetrics がモデルをデータに当てはめないため、 $β_{1}$ は変更されません。

パフォーマンスメトリクスを追跡するためのインクリメンタルモデルの構成

ライブスクリプトを開く

バイナリ分類用のインクリメンタル線形 SVM モデルを作成します。推定期間を 5,000 個の観測値に指定し、SGD ソルバーを指定します。

Mdl = incrementalClassificationLinear('EstimationPeriod',5000,'Solver','sgd')

Mdl = 
  incrementalClassificationLinear

            IsWarm: 0
           Metrics: [1x2 table]
        ClassNames: [1x0 double]
    ScoreTransform: 'none'
              Beta: [0x1 double]
              Bias: 0
           Learner: 'svm'

Mdl は incrementalClassificationLinear モデルです。そのプロパティはすべて読み取り専用です。

モデルのプロパティを照会して、モデルがウォームであるかどうかとメトリクスのウォームアップ期間のサイズを調べます。

isWarm = Mdl.IsWarm

isWarm = logical
   0

mwp = Mdl.MetricsWarmupPeriod

mwp = 1000

Mdl.IsWarm が 0; であるため、Mdl はウォームではありません。

モデルのパフォーマンスを測定する前にインクリメンタル近似関数 (fit など) で処理しなければならない観測値の数を調べます。

numObsBeforeMetrics = Mdl.MetricsWarmupPeriod + Mdl.EstimationPeriod

numObsBeforeMetrics = 6000

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

Y = Y > 2;

インクリメンタル学習を実行します。各反復で次を行います。

50 個の観測値のチャンクを処理して、データストリームをシミュレート。
updateMetrics を使用して、入力チャンクのモデルのパフォーマンスメトリクスを測定します。入力モデルを上書きします。
関数 fit を使用して、モデルを入力チャンクに当てはめます。入力モデルを上書きします。
$β_{1}$ と誤分類誤差率を保存し、インクリメンタル学習中にそれらがどのように進化するかを確認します。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
beta1 = zeros(nchunk,1);    

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;
    Mdl = updateMetrics(Mdl,X(idx,:),Y(idx));
    ce{j,:} = Mdl.Metrics{"ClassificationError",:};
    Mdl = fit(Mdl,X(idx,:),Y(idx));
    beta1(j) = Mdl.Beta(1);
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationLinear モデルオブジェクトです。

パラメーターがインクリメンタル学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(beta1)
ylabel('\beta_1')
xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.')
xlabel('Iteration')
axis tight
nexttile
plot(ce.Variables)
ylabel('ClassificationError')
xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.')
xline(numObsBeforeMetrics/numObsPerChunk,'g-.')
xlim([0 nchunk])
legend(ce.Properties.VariableNames)
xlabel(t,'Iteration')

$Figure contains 2 axes objects. Axes object 1 with xlabel Iteration, ylabel \beta_1 contains 2 objects of type line, constantline. Axes object 2 with ylabel ClassificationError contains 4 objects of type line, constantline. These objects represent Cumulative, Window.$

mdlIsWarm = numObsBeforeMetrics/numObsPerChunk

mdlIsWarm = 120

プロットは、推定期間が経過するまでは、fit がモデルをデータに当てはめることも、パラメーターを更新することもないということを示します。また、updateMetrics は、推定期間およびメトリクスのウォームアップ期間 (120 チャンク) が経過するまでは分類誤差を追跡しません。

条件付き学習の実行

ライブスクリプトを開く

線形回帰モデルのパフォーマンスが低下した場合にのみ、そのモデルに対してインクリメンタル学習を行います。

2015 年のニューヨーク市住宅データセットを読み込み、シャッフルします。このデータの詳細については、NYC Open Data を参照してください。

load NYCHousing2015

rng(1) % For reproducibility
n = size(NYCHousing2015,1);
shuffidx = randsample(n,n);
NYCHousing2015 = NYCHousing2015(shuffidx,:);

テーブルから応答変数 SALEPRICE を抽出します。数値安定性を得るために、SALEPRICE を 1e6 の尺度でスケールします。

Y = NYCHousing2015.SALEPRICE/1e6;
NYCHousing2015.SALEPRICE = [];

カテゴリカル予測子からダミー変数メトリクスを作成します。

catvars = ["BOROUGH" "BUILDINGCLASSCATEGORY" "NEIGHBORHOOD"];
dumvarstbl = varfun(@(x)dummyvar(categorical(x)),NYCHousing2015,...
    'InputVariables',catvars);
dumvarmat = table2array(dumvarstbl);
NYCHousing2015(:,catvars) = [];

テーブル内の他のすべての数値変数を売価の線形予測子として扱います。ダミー変数の行列を残りの予測子データに連結し、データを転置して計算を高速化します。

idxnum = varfun(@isnumeric,NYCHousing2015,'OutputFormat','uniform');
X = [dumvarmat NYCHousing2015{:,idxnum}]';

推定期間またはメトリクスのウォームアップ期間がないように、インクリメンタル学習用の線形回帰モデルを構成します。メトリクスウィンドウサイズを観測値 1000 個に指定します。構成したモデルを最初の 100 個の観測値に当てはめて、観測値がデータの列に沿うように指定します。

Mdl = incrementalRegressionLinear('EstimationPeriod',0,'MetricsWarmupPeriod',0,...
    'MetricsWindowSize',1000);
numObsPerChunk = 100;
Mdl = fit(Mdl,X(:,1:numObsPerChunk),Y(1:numObsPerChunk),'ObservationsIn','columns');

Mdl は incrementalRegressionLinear モデルオブジェクトです。

条件付きの当てはめを行い、インクリメンタル学習を実行します。各反復でこの手順に従います。

100 個の観測値のチャンクを処理して、データストリームをシミュレートします。
サイズが 200 の観測ウィンドウ内で、イプシロン不感応損失を計算することにより、モデルパフォーマンスを更新します。観測値がデータの列に沿うように指定します。
それまでの最小損失の倍を超える損失が発生した場合にのみ、モデルをデータチャンクに当てはめます。観測値がデータの列に沿うように指定します。
パフォーマンスと当てはめを追跡するときは、前のインクリメンタルモデルを上書きします。
イプシロン不感応損失と $β_{313}$ を保存して、損失と係数が学習中にどのように進化するかを確認します。
fit がモデルに学習させるタイミングを追跡します。

% Preallocation
n = numel(Y) - numObsPerChunk;
nchunk = floor(n/numObsPerChunk);
beta313 = zeros(nchunk,1);
ei = array2table(nan(nchunk,2),'VariableNames',["Cumulative" "Window"]);
trained = false(nchunk,1);

% Incremental fitting
for j = 2:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;
    Mdl = updateMetrics(Mdl,X(:,idx),Y(idx),'ObservationsIn','columns');
    ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:};
    minei = min(ei{:,2});
    pdiffloss = (ei{j,2} - minei)/minei*100;
    if pdiffloss > 100
        Mdl = fit(Mdl,X(:,idx),Y(idx),'ObservationsIn','columns');
        trained(j) = true;
    end    
    beta313(j) = Mdl.Beta(end);
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalRegressionLinear モデルオブジェクトです。

モデルのパフォーマンスと $β_{313}$ が学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(beta313)
hold on
plot(find(trained),beta313(trained),'r.')
xlim([0 nchunk])
ylabel('\beta_{313}')
xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.')
legend('\beta_{313}','Training occurs','Location','southeast')
hold off
nexttile
plot(ei.Variables)
xlim([0 nchunk])
ylabel('Epsilon Insensitive Loss')
xline(Mdl.EstimationPeriod/numObsPerChunk,'r-.')
legend(ei.Properties.VariableNames)
xlabel(t,'Iteration')

$Figure contains 2 axes objects. Axes object 1 with ylabel \beta_{313} contains 3 objects of type line, constantline. One or more of the lines displays its values using only markers These objects represent \beta_{313}, Training occurs. Axes object 2 with ylabel Epsilon Insensitive Loss contains 3 objects of type line, constantline. These objects represent Cumulative, Window.$

$β_{313}$ のトレースプロットは、損失がそれまでの最小損失の倍とならない定数値の期間を示します。

入力引数

すべて折りたたむ

`Mdl` — インクリメンタル学習モデル
`incrementalClassificationLinear` モデルオブジェクト | `incrementalRegressionLinear` モデルオブジェクト

パフォーマンスを測定するインクリメンタル学習モデル。incrementalClassificationLinear または incrementalRegressionLinear というモデルオブジェクトとして指定します。Mdl は、直接作成することも、サポートされている従来式の学習済み機械学習モデルを関数 incrementalLearner によって変換して作成することもできます。詳細については、対応するリファレンスページを参照してください。

Mdl.IsWarm が false の場合、updateMetrics はモデルのパフォーマンスを追跡しません。updateMetrics がパフォーマンスメトリクスを追跡する前に、Mdl とデータを fit に渡して、Mdl を Mdl.EstimationPeriod + Mdl.MetricsWarmupPeriod 観測値に当てはめなければなりません。詳細は、パフォーマンスメトリクスを参照してください。

`X` — 予測子データのチャンク
浮動小数点行列

モデルのパフォーマンスを測定する予測子データのチャンク。n 個の観測値および Mdl.NumPredictors 予測子変数の浮動小数点行列として指定します。名前と値の引数 ObservationsIn の値は、変数と観測値の方向を決定します。ObservationsIn の既定値は "rows" であり、予測子データの観測値が X の行に沿うことを示しています。

観測値のラベル Y の長さと X の観測値の数は同じでなければなりません。Y(j) は X 内の観測値 j (行または列) のラベルです。

メモ

Mdl.NumPredictors = 0 の場合、updateMetrics は X から予測子の数を推測し、出力モデルの対応するプロパティを設定します。それ以外の場合、ストリーミングデータ内の予測子変数の数が Mdl.NumPredictors から変化すると、updateMetrics がエラーを生成します。
updateMetrics は、浮動小数点の入力予測子データのみをサポートしています。入力データに categorical データが含まれている場合は、エンコードバージョンの categorical データを準備する必要があります。dummyvar を使用して、各カテゴリカル変数をダミー変数で構成される数値行列に変換します。その後、すべてのダミー変数行列とその他の数値予測子を連結します。詳細については、ダミー変数を参照してください。

データ型: single | double

`Y` — 応答 (ラベル) のチャンク
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

モデルのパフォーマンスを測定する応答 (ラベル) のチャンク。分類問題では、categorical 配列、文字配列、string 配列、logical ベクトル、浮動小数点ベクトル、または文字ベクトルの cell 配列として指定します。回帰問題では、浮動小数点ベクトルとして指定します。

観測値のラベル Y の長さと X の観測値の数は同じでなければなりません。Y(j) は X 内の観測値 j (行または列) のラベルです。

分類問題では次のようになります。

updateMetrics はバイナリ分類のみをサポートします。
入力モデル Mdl の ClassNames プロパティが空以外の場合は、次の条件が適用されます。
- Y が Mdl.ClassNames のメンバーではないラベルを含む場合、updateMetrics はエラーを生成します。
- Y と Mdl.ClassNames のデータ型は同じでなければなりません。

メモ

観測値 (予測子またはラベル) または重みが少なくとも 1 つの欠損 (NaN) 値を含む場合、updateMetrics はその観測値を無視します。したがって、updateMetrics は n 個よりも少ない観測値を使用してモデルパフォーマンスを計算します。ここで n は X 内の観測値数です。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'ObservationsIn','columns','Weights',W は、予測子行列の列が観測値に対応すること、およびインクリメンタル学習中に適用する観測値の重みがベクトル W に格納されていることを指定します。

`ObservationsIn` — 予測子データにおける観測値の次元
`'rows'` (既定値) | `'columns'`

予測子データにおける観測値の次元。'ObservationsIn' と 'columns' または 'rows' から構成されるコンマ区切りのペアとして指定します。

データ型: char | string

`Weights` — 観測値の重みのチャンク
正の値の浮動小数点ベクトル

観測値の重みのチャンク。'Weights' と正の値の浮動小数点ベクトルで構成されるコンマ区切りのペアとして指定します。updateMetrics は、Weights 内の対応する値を使用して X 内の観測値に重みを付けます。Weights のサイズは X 内の観測値の数 n と同じでなければなりません。

既定では Weights は ones(n,1) です。

正規化方式を含む詳細については、観測値の重みを参照してください。

データ型: double | single

出力引数

すべて折りたたむ

`Mdl` — 更新されたインクリメンタル学習モデル
`incrementalClassificationLinear` モデルオブジェクト | `incrementalRegressionLinear` モデルオブジェクト

更新されたインクリメンタル学習モデル。incrementalClassificationLinear または incrementalRegressionLinear の入力モデル Mdl と同じデータ型のインクリメンタル学習モデルオブジェクトとして返されます。

モデルがウォームでない場合、updateMetrics はパフォーマンスメトリクスを計算しません。その結果、Mdl の Metrics プロパティは、NaN 値で構成された状態を完全に維持します。モデルがウォームの場合、updateMetrics は、新しいデータ X と Y における累積およびウィンドウのパフォーマンスメトリクスを計算し、Mdl.Metrics の対応する要素を上書きします。入力モデル Mdl の他のプロパティは、すべて出力モデル Mdl に引き継がれます。詳細は、パフォーマンスメトリクスを参照してください。

ヒント

従来式の学習とは異なり、インクリメンタル学習には個別のテスト (ホールドアウト) セットが存在しない場合もあります。そのため、データの各入力チャンクをテストセットとして扱うには、インクリメンタルモデルと各入力チャンクを、fit を使用して同じデータでモデルに学習させる前に updateMetrics に渡します。

アルゴリズム

すべて折りたたむ

パフォーマンスメトリクス

updateMetrics は、インクリメンタルモデルが "ウォーム" (IsWarm プロパティが true) のときに、Mdl.Metrics のテーブルの行ラベルによって指定され、新しいデータから得られるモデルのパフォーマンスメトリクスのみを追跡します。インクリメンタルモデルは、関数 fit がインクリメンタルモデルを Mdl.MetricsWarmupPeriod の観測値 ("メトリクスのウォームアップ期間") に当てはめた後、ウォームになります。
Mdl.EstimationPeriod > 0 の場合、関数はモデルをデータに当てはめる前にハイパーパラメーターを推定します。そのため、関数は、モデルがメトリクスのウォームアップ期間を開始する前に EstimationPeriod 個の観測値を追加で処理しなければなりません。
インクリメンタルモデルの Metrics プロパティは、各パフォーマンスメトリクスの 2 つの形式を table の変数 (列) Cumulative および Window とし、個々のメトリクスを行に格納します。インクリメンタルモデルがウォームになると、updateMetrics は次の頻度でメトリクスを更新します。
- Cumulative — 関数は、モデルの性能追跡の開始以降の累積メトリクスを計算します。関数は、関数が呼び出されるたびにメトリクスを更新し、提供されたデータセット全体に基づいて計算を行います。
- Window — 関数は、Mdl.MetricsWindowSize プロパティによって決定されたウィンドウ内のすべての観測値に基づいてメトリクスを計算します。Mdl.MetricsWindowSize によってソフトウェアが Window メトリクスを更新する頻度も決まります。たとえば、Mdl.MetricsWindowSize が 20 の場合、関数は提供されたデータの最後の 20 個の観測値に基づいてメトリクスを計算します (X((end – 20 + 1):end,:) および Y((end – 20 + 1):end))。
  ウィンドウ内のパフォーマンスメトリクスを追跡するインクリメンタル関数は、次のプロセスを使用します。
  1. 指定された各メトリクスについて長さ Mdl.MetricsWindowSize のバッファーを保存し、観測値の重みのバッファーを保存します。
  2. 入力観測値のバッチに基づくモデル性能をメトリクスバッファーの要素に入力し、対応する観測値の重みを重みバッファーに格納します。
  3. バッファーがいっぱいになると、Mdl.Metrics.Window をメトリクスウィンドウの性能の加重平均で上書きします。関数が観測値のバッチを処理するときにバッファーがあふれる場合、最新の入力観測値 Mdl.MetricsWindowSize がバッファーに入り、最も古い観測値がバッファーから削除されます。たとえば、Mdl.MetricsWindowSize が 20 で、メトリクスバッファーには前に処理されたバッチからの 10 個の値が存在し、15 個の値が入力されるとします。長さ 20 のウィンドウを構成するため、関数は 15 個の入力観測値からの測定値と前のバッチからの最新の 5 個の測定値を使用します。
Cumulative と Window のパフォーマンスメトリクスの値を計算する際、予測 (分類の場合はスコア、回帰の場合は応答) が NaN の観測値は省略されます。

観測値の重み

分類問題では、クラスの事前確率分布が既知の場合 (つまり、事前分布が経験的分布でない場合)、updateMetrics は、観測値の重みを正規化して、それぞれのクラスの事前クラス確率の合計になるようにします。このアクションは、観測値の重みが既定でそれぞれのクラスの事前確率であることを前提としています。

回帰問題の場合、またはクラスの事前確率分布が経験的分布の場合、ソフトウェアは、updateMetrics が呼び出されるたびに、指定された観測値の重みを正規化して、合計が 1 になるようにします。

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

saveLearnerForCoder、loadLearnerForCoder および codegen (MATLAB Coder) を使用して、関数 updateMetrics のコードを生成します。saveLearnerForCoder を使用して、学習済みモデルを保存します。loadLearnerForCoder を使用して保存済みモデルを読み込んで関数 updateMetrics を呼び出す、エントリポイント関数を定義します。次に、codegen を使用して、エントリポイント関数のコードを生成します。
updateMetrics 用の単精度 C/C++ コードを生成するには、関数 loadLearnerForCoder を呼び出すときに名前と値の引数 "DataType","single" を指定します。

次の表は、updateMetrics の引数に関する注意です。この表に含まれていない引数は、完全にサポートされています。

引数注意と制限

引数	注意と制限
`Mdl`	モデルオブジェクトの使用上の注意および制限については、`incrementalClassificationLinear` または `incrementalRegressionLinear` を参照してください。
`X`	バッチ間の観測値の数は可変サイズにすることができますが、対応する `Y` の観測値の数と等しくなければなりません。予測子変数の数は `Mdl.NumPredictors` と等しくなければなりません。 `X` は `single` または `double` でなければなりません。
`Y`	バッチ間の観測値の数は可変サイズにすることができますが、対応する `X` の観測値の数と等しくなければなりません。分類問題では、`Y` のすべてのラベルを `Mdl.ClassNames` で表さなければなりません。 `Y` と `Mdl.ClassNames` は同じデータ型でなければなりません。

Mdl

モデルオブジェクトの使用上の注意および制限については、incrementalClassificationLinear または incrementalRegressionLinear を参照してください。

X

バッチ間の観測値の数は可変サイズにすることができますが、対応する Y の観測値の数と等しくなければなりません。
予測子変数の数は Mdl.NumPredictors と等しくなければなりません。
X は single または double でなければなりません。

Y

バッチ間の観測値の数は可変サイズにすることができますが、対応する X の観測値の数と等しくなければなりません。
分類問題では、Y のすべてのラベルを Mdl.ClassNames で表さなければなりません。
Y と Mdl.ClassNames は同じデータ型でなければなりません。

次の制限が適用されます。
- データをシャッフルするように Mdl を構成した場合 (Mdl.Shuffle が true であるか、Mdl.Solver が 'sgd' または 'asgd')、関数 updateMetrics は、モデルをバッチに当てはめる前に観測値の各入力バッチを無作為にシャッフルします。シャッフルされた観測値の順序は、MATLAB^® で生成される順序と一致しないことがあります。したがって、パフォーマンスメトリクスを更新する前に Mdl を当てはめた場合、MATLAB で計算されるメトリクスと生成コードで計算されるメトリクスが等しくならない場合があります。
- 浮動小数点の入力引数およびオブジェクトプロパティには、すべて同質なデータ型を使用します。具体的には、single または double のいずれかです。

詳細は、コード生成の紹介を参照してください。

バージョン履歴

R2020b で導入

参考

オブジェクト

incrementalClassificationLinear | incrementalRegressionLinear

関数

updateMetricsAndFit | fit | loss

updateMetrics

構文

説明

例

インクリメンタル モデルのパフォーマンスの追跡

パフォーマンス メトリクスを追跡するためのインクリメンタル モデルの構成

条件付き学習の実行

入力引数

Mdl — インクリメンタル学習モデル incrementalClassificationLinear モデル オブジェクト | incrementalRegressionLinear モデル オブジェクト

X — 予測子データのチャンク 浮動小数点行列

Y — 応答 (ラベル) のチャンク categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

名前と値の引数

ObservationsIn — 予測子データにおける観測値の次元 'rows' (既定値) | 'columns'

Weights — 観測値の重みのチャンク 正の値の浮動小数点ベクトル

出力引数

Mdl — 更新されたインクリメンタル学習モデル incrementalClassificationLinear モデル オブジェクト | incrementalRegressionLinear モデル オブジェクト

ヒント

アルゴリズム

パフォーマンス メトリクス

観測値の重み

拡張機能

C/C++ コード生成 MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

参考

オブジェクト

関数

トピック

インクリメンタルモデルのパフォーマンスの追跡

パフォーマンスメトリクスを追跡するためのインクリメンタルモデルの構成

`Mdl` — インクリメンタル学習モデル
`incrementalClassificationLinear` モデルオブジェクト | `incrementalRegressionLinear` モデルオブジェクト

`X` — 予測子データのチャンク
浮動小数点行列

`Y` — 応答 (ラベル) のチャンク
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

`ObservationsIn` — 予測子データにおける観測値の次元
`'rows'` (既定値) | `'columns'`

`Weights` — 観測値の重みのチャンク
正の値の浮動小数点ベクトル

`Mdl` — 更新されたインクリメンタル学習モデル
`incrementalClassificationLinear` モデルオブジェクト | `incrementalRegressionLinear` モデルオブジェクト

パフォーマンスメトリクス

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。