loss

データのバッチでの線形インクリメンタル学習モデルの損失

R2020b 以降

構文

L = loss(Mdl,X,Y)

L = loss(Mdl,X,Y,Name,Value)

説明

loss は、線形回帰 (incrementalRegressionLinear オブジェクト) または線形バイナリ分類 (incrementalClassificationLinear オブジェクト) 用に構成されたインクリメンタル学習モデルの回帰損失または分類損失を返します。

データ ストリームでのモデルの性能を測定し、結果を出力モデルに保存するには、updateMetrics または updateMetricsAndFit を呼び出します。

L = loss(Mdl,X,Y) は、予測子データ X および対応する応答 Y のバッチを使用して、インクリメンタル学習モデル Mdl の損失を返します。

L = loss(Mdl,X,Y,Name,Value) は、1 つ以上の名前と値のペアの引数によって指定された追加オプションを使用します。たとえば、予測子データ行列の列が観測値に対応するように指定したり、分類損失関数を指定したりできます。

例

インクリメンタル学習中のモデルの性能の測定

ストリーミング データでのインクリメンタル モデルの性能を 3 通りの方法で測定します。

1. 累積メトリクスで、インクリメンタル学習の開始以降の性能を測定します。

2. ウィンドウ メトリクスで、指定した観測値ウィンドウでの性能を測定します。指定したウィンドウをモデルが処理するたびにメトリクスが更新されます。

3. 関数 loss で、指定したデータのバッチについてのみ性能を測定します。

人の行動のデータ セットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データ セットの詳細については、コマンド ラインで Description を入力してください。

応答は、次の 5 つのクラスのいずれかになります。座る、立つ、歩く、走る、または踊る。被験者が移動しているかどうか (actid > 2) を基準に、応答を二分します。

Y = Y > 2;

バイナリ分類用のインクリメンタル線形 SVM モデルを作成します。クラス名、前のクラスの分布 (一様)、および任意の係数とバイアス値を指定して loss 用にモデルを構成します。メトリクス ウィンドウ サイズを観測値 1000 個に指定します。

p = size(X,2);
Beta = randn(p,1);
Bias = randn(1);
Mdl = incrementalClassificationLinear('Beta',Beta,'Bias',Bias, ...
    'ClassNames',unique(Y),'Prior','uniform','MetricsWindowSize',1000);

Mdl は incrementalClassificationLinear モデルです。そのプロパティはすべて読み取り専用です。任意の値を指定する代わりに、次のいずれかのアクションを実行してモデルを構成できます。

• fitcsvm または fitclinear を使用してデータのサブセット (利用可能な場合) で SVM モデルに学習させた後、incrementalLearner を使用してモデルをインクリメンタル学習器に変換します。

• fit を使用して、Mdl をデータに漸増的に当てはめます。

データ ストリームをシミュレートし、50 個の観測値の入力チャンクごとに次のアクションを実行します。

1. updateMetrics を呼び出して、累積性能および観測値ウィンドウ内での性能を測定します。前のインクリメンタル モデルを新しいモデルで上書きして、パフォーマンス メトリクスを追跡します。

2. loss を呼び出して、入力チャンクでのモデルの性能を測定します。

3. fit を呼び出して、モデルを入力チャンクに当てはめます。前のインクリメンタル モデルを、入力観測値に当てはめた新しいモデルで上書きします。

4. すべてのパフォーマンス メトリクスを保存して、インクリメンタル学習中にそれらがどのように進化するかを確認します。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ce = array2table(zeros(nchunk,3),'VariableNames',["Cumulative" "Window" "Loss"]);

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetrics(Mdl,X(idx,:),Y(idx));
    ce{j,["Cumulative" "Window"]} = Mdl.Metrics{"ClassificationError",:};
    ce{j,"Loss"} = loss(Mdl,X(idx,:),Y(idx));
    Mdl = fit(Mdl,X(idx,:),Y(idx));
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationLinear モデル オブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetrics は入力観測値でのモデルの性能をチェックし、関数 fit はモデルをその観測値に当てはめます。loss はメトリクスのウォームアップ期間に依存しないため、すべての反復について分類誤差を測定します。

パフォーマンス メトリクスが学習中にどのように進化するかを確認するには、それらをプロットします。

figure
plot(ce.Variables)
xlim([0 nchunk])
ylim([0 0.05])
ylabel('Classification Error')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.')
legend(ce.Properties.VariableNames)
xlabel('Iteration')

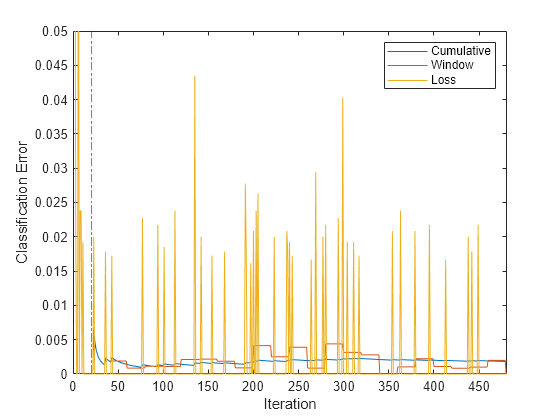
黄色の線は、入力データの各チャンクの分類誤差を表します。メトリクスのウォームアップ期間後、Mdl は累積およびウィンドウ メトリクスを追跡します。累積およびバッチ損失は、関数 fit が入力データにインクリメンタル モデルを当てはめるにつれて収束します。

データの入力チャンクでのカスタム損失の計算

ストリーミング データに回帰用のインクリメンタル学習モデルを当てはめ、入力データのバッチの平均絶対偏差 (MAD) を計算します。

ロボット アームのデータ セットを読み込みます。標本サイズ n と予測子変数の数 p を取得します。

load robotarm
n = numel(ytrain);
p = size(Xtrain,2);

データ セットの詳細については、コマンド ラインで Description を入力してください。

回帰用のインクリメンタル線形モデルを作成します。次のようにモデルを構成します。

• メトリクスのウォームアップ期間を観測値 1000 個に指定します。

• メトリクス ウィンドウ サイズを観測値 500 個に指定します。

• 平均絶対偏差 (MAD) を追跡して、モデルの性能を測定します。新しい各観測値の絶対誤差を測定する無名関数を作成します。名前 MeanAbsoluteError とそれに対応する関数を含む構造体配列を作成します。

• すべての回帰係数およびバイアスを 0 に指定して、モデルを応答予測用に構成します。

maefcn = @(z,zfit,w)(abs(z - zfit));
maemetric = struct("MeanAbsoluteError",maefcn);

Mdl = incrementalRegressionLinear('MetricsWarmupPeriod',1000,'MetricsWindowSize',500, ...
    'Metrics',maemetric,'Beta',zeros(p,1),'Bias',0,'EstimationPeriod',0)

Mdl = 
  incrementalRegressionLinear

               IsWarm: 0
              Metrics: [2x2 table]
    ResponseTransform: 'none'
                 Beta: [32x1 double]
                 Bias: 0
              Learner: 'svm'

Mdl はインクリメンタル学習用に構成された incrementalRegressionLinear モデル オブジェクトです。

インクリメンタル学習を実行します。各反復で次を行います。

• 50 個の観測値のチャンクを処理して、データ ストリームをシミュレートします。

• updateMetrics を呼び出して、データの入力チャンクの累積メトリクスとウィンドウ メトリクスを計算します。前のインクリメンタル モデルを、前のメトリクスを上書きするように当てはめた新しいモデルで上書きします。

• loss を呼び出して、データの入力チャンクの MAD を計算します。累積メトリクスおよびウィンドウ メトリクスでは、カスタム損失が各観測値の損失を返す必要がありますが、loss ではチャンク全体での損失が必要です。絶対偏差の平均を計算します。

• fit を呼び出して、データの入力チャンクにインクリメンタル モデルを当てはめます。

• 累積、ウィンドウ、およびチャンクのメトリクスを保存して、インクリメンタル学習中にそれらがどのように進化するかを確認します。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
mae = array2table(zeros(nchunk,3),'VariableNames',["Cumulative" "Window" "Chunk"]);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetrics(Mdl,Xtrain(idx,:),ytrain(idx));
    mae{j,1:2} = Mdl.Metrics{"MeanAbsoluteError",:};
    mae{j,3} = loss(Mdl,Xtrain(idx,:),ytrain(idx),'LossFun',@(x,y,w)mean(maefcn(x,y,w)));
    Mdl = fit(Mdl,Xtrain(idx,:),ytrain(idx));
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalRegressionLinear モデル オブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetrics は入力観測値でのモデルの性能をチェックし、関数 fit はモデルをその観測値に当てはめます。

パフォーマンス メトリクスをプロットして、インクリメンタル学習中にそれらがどのように進化したかを確認します。

figure
h = plot(mae.Variables);
xlim([0 nchunk])
ylabel('Mean Absolute Deviation')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.')
xlabel('Iteration')
legend(h,mae.Properties.VariableNames)

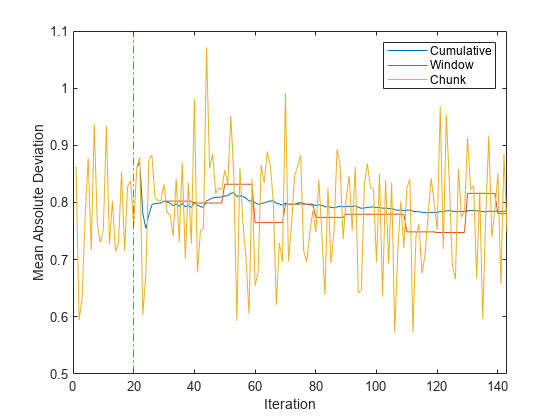
プロットは次のことを示しています。

• updateMetrics は、パフォーマンス メトリクスをメトリクスのウォームアップ期間後にのみ計算します。

• updateMetrics は、累積メトリクスを各反復中に計算します。

• updateMetrics は、ウィンドウ メトリクスを 500 個の観測値の処理後に計算します。

• Mdl が観測値の予測のためにインクリメンタル学習の初めから構成されたため、loss はデータの入力チャンクごとに MAD を計算できます。

入力引数

Mdl — インクリメンタル学習モデル

incrementalClassificationLinear モデル オブジェクト | incrementalRegressionLinear モデル オブジェクト

インクリメンタル学習モデル。incrementalClassificationLinear または incrementalRegressionLinear というモデル オブジェクトとして指定します。Mdl は、直接作成することも、サポートされている従来式の学習済み機械学習モデルを関数 incrementalLearner によって変換して作成することもできます。詳細については、対応するリファレンス ページを参照してください。

Mdl は、観測値のバッチでの損失を計算するように構成しなければなりません。

• Mdl が従来式の学習済みモデルから変換される場合、いかなる修正も行うことなく損失を計算できます。

• そうでない場合、Mdl が次の基準を満たすように、直接指定するか、fit または updateMetricsAndFit を使用して Mdl をデータに当てはめなければなりません。

  • Mdl が incrementalRegressionLinear モデルである場合、そのモデル係数 Mdl.Beta およびバイアス Mdl.Bias は空でない配列でなければなりません。

  • Mdl が incrementalClassificationLinear モデルである場合、そのモデル係数 Mdl.Beta およびバイアス Mdl.Bias は空でない配列でなければならず、クラス名 Mdl.ClassNames は 2 つのクラスを含んでいなければなりません。また、前のクラスの分布 Mdl.Prior は既知の値を含んでいなければなりません。

  • オブジェクト タイプにかかわらず、関数が予測子データを標準化するようにモデルを構成する場合、予測子の平均 Mdl.Mu および標準偏差 Mdl.Sigma は空でない配列でなければなりません。

X — 予測子データのバッチ

浮動小数点行列

損失を計算するための予測子データのバッチ。n 個の観測値および Mdl.NumPredictors 予測子変数の浮動小数点行列として指定します。名前と値の引数 ObservationsIn の値は、変数と観測値の方向を決定します。ObservationsIn の既定値は "rows" であり、予測子データの観測値が X の行に沿うことを示しています。

観測値のラベル Y の長さと X の観測値の数は同じでなければなりません。Y(j) は X 内の観測値 j (行または列) のラベルです。

メモ

loss は、浮動小数点の入力予測子データのみをサポートしています。入力データに categorical データが含まれている場合は、エンコード バージョンの categorical データを準備する必要があります。dummyvar を使用して、各カテゴリカル変数をダミー変数で構成される数値行列に変換します。その後、すべてのダミー変数行列とその他の数値予測子を連結します。詳細については、ダミー変数を参照してください。

データ型: single | double

Y — 応答 (ラベル) のバッチ

categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

損失を計算する応答 (ラベル) のバッチ。分類問題では、categorical 配列、文字配列、string 配列、logical ベクトル、浮動小数点ベクトル、または文字ベクトルの cell 配列として指定します。回帰問題では、浮動小数点ベクトルとして指定します。

観測値のラベル Y の長さと X の観測値の数は同じでなければなりません。Y(j) は X 内の観測値 j (行または列) のラベルです。

分類問題では次のようになります。

• loss はバイナリ分類のみをサポートします。

• Y が Mdl.ClassNames のメンバーではないラベルを含む場合、loss はエラーを生成します。

• Y と Mdl.ClassNames のデータ型は同じでなければなりません。

データ型: char | string | cell | categorical | logical | single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'ObservationsIn','columns','Weights',W は、予測子行列の列が観測値に対応すること、および適用する観測値の重みがベクトル W に格納されていることを指定します。

LossFun — 損失関数

string ベクトル | 関数ハンドル | cell ベクトル | 構造体配列

損失関数。'LossFun' と組み込み損失関数名または関数ハンドルから構成されるコンマ区切りのペアとして指定します。

• 分類問題: 次の表は、Mdl が incrementalClassificationLinear モデルであるときに使用可能な損失関数の一覧です。対応する文字ベクトルまたは string スカラーを使用して、いずれかを指定します。

  名前	説明
  "binodeviance"	二項分布からの逸脱度
  "classiferror" (既定の設定)	10 進数の誤分類率
  "exponential"	指数損失
  "hinge"	ヒンジ損失
  "logit"	ロジスティック損失
  "quadratic"	二次損失

  詳細については、分類損失を参照してください。

  ロジスティック回帰学習器は事後確率を分類スコアとして返しますが、SVM 学習器はそうではありません (predict を参照)。

  カスタム損失関数を指定するには、関数ハンドル表記を使用します。関数は次の形式でなければなりません。

  lossval = lossfcn(C,S,W)

  • 出力引数 lossval は n 行 1 列の浮動小数点ベクトルです。lossval(j) は観測値 j の分類損失です。

  • 関数名 (lossfcn) を指定します。

  • C は n 行 2 列の logical 行列であり、対応する観測値が属するクラスを各行が示します。列の順序は ClassNames プロパティのクラスの順序に対応します。C を作成するには、指定されたデータの各観測値について観測値 p がクラス q に属する場合に C(p,q) = 1 を設定します。行 p の他の要素を 0 に設定します。

  • S は、予測分類スコアの n 行 2 列の数値行列です。S は predict の出力 score に似ています。ここで、行はデータの観測値に対応し、列の順序は ClassNames プロパティのクラスの順序に対応しています。S(p,q) は、クラス q に分類されている観測値 p の分類スコアです。

  • W は、観測値の重みの n 行 1 列の数値ベクトルです。

• 回帰問題: 次の表は、Mdl が incrementalRegressionLinear モデルであるときに使用可能な損失関数の一覧です。対応する文字ベクトルまたは string スカラーを使用して、いずれかを指定します。

  名前	説明	メトリクスをサポートする学習器
  "epsiloninsensitive"	イプシロン不感応損失	'svm'
  "mse" (既定の設定)	重み付けされた平均二乗誤差	'svm' および 'leastsquares'

  詳細については、回帰損失を参照してください。

  カスタム損失関数を指定するには、関数ハンドル表記を使用します。関数は次の形式でなければなりません。

  lossval = lossfcn(Y,YFit,W)

  • 出力引数 lossval は浮動小数点スカラーです。

  • 関数名 (lossfcn) を指定します。

  • Y は、観測応答の長さ n の数値ベクトルです。

  • YFit は、対応する予測応答の長さ n の数値ベクトルです。

  • W は、観測値の重みの n 行 1 列の数値ベクトルです。

例: 'LossFun',"mse"

例: 'LossFun',@lossfcn

データ型: char | string | function_handle

ObservationsIn — 予測子データにおける観測値の次元

'rows' (既定値) | 'columns'

予測子データにおける観測値の次元。'ObservationsIn' と 'columns' または 'rows' から構成されるコンマ区切りのペアとして指定します。

データ型: char | string

Weights — 観測値の重みのバッチ

正の値の浮動小数点ベクトル

観測値の重みのバッチ。'Weights' と正の値の浮動小数点ベクトルで構成されるコンマ区切りのペアとして指定します。loss は、Weights 内の対応する値を使用して入力データ内の観測値に重みを付けます。Weights のサイズは入力データ内の観測値の数 n と同じでなければなりません。

既定では Weights は ones(n,1) です。

詳細は、観測値の重みを参照してください。

データ型: double | single

出力引数

L — 分類損失または回帰損失

数値スカラー

分類損失または回帰損失。数値スカラーとして返されます。L の解釈は Weights と LossFun によって異なります。

詳細

分類損失

"分類損失" 関数は分類モデルの予測誤差を評価します。複数のモデルで同じタイプの損失を比較した場合、損失が低い方が予測モデルとして優れていることになります。

以下のシナリオを考えます。

• L は加重平均分類損失です。

• n は標本サイズです。

• y_j は観測されたクラス ラベルです。陰性クラスを示す -1 または陽性クラスを示す 1 (あるいは、ClassNames プロパティの最初のクラスを示す -1 または 2 番目のクラスを示す 1) を使用して符号化されます。

• f(X_j) は予測子データ X の観測値 (行) j に対する陽性クラスの分類スコアです。

• m_j = y_jf(X_j) は、y_j に対応するクラスに観測値 j を分類する分類スコアです。正の値の m_j は正しい分類を示しており、平均損失に対する寄与は大きくありません。負の値の m_j は正しくない分類を示しており、平均損失に大きく寄与します。

• 観測値 j の重みは w_j です。

この状況では、名前と値の引数 LossFun を使用して指定できる、サポートされる損失関数は次の表のようになります。

損失関数	LossFun の値	式
二項分布からの逸脱度	"binodeviance"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left\{1+\exp \left[-2m_j\right]\right\}}.$$
指数損失	"exponential"	$$L={\displaystyle \sum _{j=1}^n{w}_j\exp \left(-m_j\right)}.$$
10 進数の誤分類率	"classiferror"	$$L={\displaystyle \sum _{j=1}^n{w}_j}I\left\{{\widehat{y}}_j\ne y_j\right\},$$ ここで、$${\widehat{y}}_j$$ はスコアが最大であるクラスに対応するクラス ラベル、I{·} はインジケーター関数です。
ヒンジ損失	"hinge"	$$L={\displaystyle \sum }_{j=1}^n{w}_j\max \left\{0,1-m_j\right\}.$$
ロジット損失	"logit"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left(1+\exp \left(-m_j\right)\right)}.$$
二次損失	"quadratic"	$$L={\displaystyle \sum _{j=1}^n{w}_j{\left(1-m_j\right)}^2}.$$

関数 loss で加重平均損失を計算する際、スコアが NaN の観測値は省略されません。そのため、予測子データ X に欠損値があり、名前と値の引数 LossFun が "classiferror" として指定されていない場合に、loss で NaN が返されることがあります。ほとんどの場合、データ セットに予測子の欠損がなければ、関数 loss で NaN が返されることはありません。

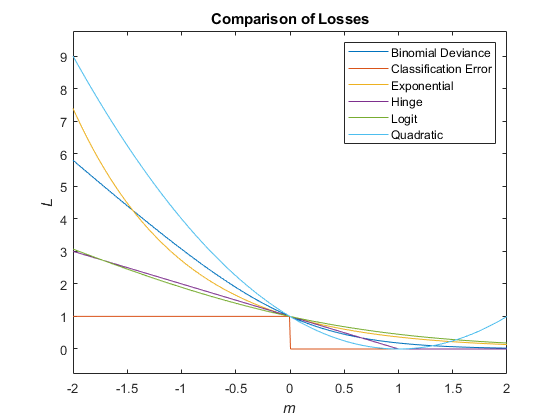
次の図では、1 つの観測値のスコア m に対する損失関数を比較しています。いくつかの関数は、点 (0,1) を通過するように正規化されています。

回帰損失

"回帰損失" 関数は、回帰モデルの予測誤差を評価します。複数のモデルで同じタイプの損失を比較した場合、損失が低い方が予測モデルとして優れていることになります。

以下のシナリオを考えます。

• L は加重平均分類損失です。

• n は標本サイズです。

• y_j は、観測値 j の観測された応答です。

• f(X_j) は、予測子データ X の観測値 j の予測値です。

• 観測値 j の重みは w_j です。

この状況では、名前と値の引数 LossFun を使用して指定できる、サポートされる損失関数は次の表のようになります。

損失関数	LossFun の値	式
イプシロン不感応損失	"epsiloninsensitive"	$$L=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right].$$
平均二乗誤差	"mse"	$$L={\left[y-f\left(x\right)\right]}^2.$$

関数 loss で加重平均損失を計算する際、予測が NaN の観測値は省略されません。そのため、予測子データ X に欠損値がある場合に loss で NaN が返されることがあります。ほとんどの場合、データ セットに予測子の欠損がなければ、関数 loss で NaN が返されることはありません。

アルゴリズム

観測値の重み

分類問題では、クラスの事前確率分布が既知の場合 (つまり、事前分布が経験的分布でない場合)、loss は、観測値の重みを正規化して、それぞれのクラスの事前クラス確率の合計になるようにします。このアクションは、観測値の重みが既定でそれぞれのクラスの事前確率であることを前提としています。

回帰問題の場合、またはクラスの事前確率分布が経験的分布の場合、ソフトウェアは、loss が呼び出されるたびに、指定された観測値の重みを正規化して、合計が 1 になるようにします。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• saveLearnerForCoder、loadLearnerForCoder および codegen (MATLAB Coder) を使用して、関数 loss のコードを生成します。saveLearnerForCoder を使用して、学習済みモデルを保存します。loadLearnerForCoder を使用して保存済みモデルを読み込んで関数 loss を呼び出す、エントリポイント関数を定義します。次に、codegen を使用して、エントリポイント関数のコードを生成します。

• loss 用の単精度 C/C++ コードを生成するには、関数 loadLearnerForCoder を呼び出すときに名前と値の引数 "DataType","single" を指定します。

• 次の表は、loss の引数に関する注意です。この表に含まれていない引数は、完全にサポートされています。

  引数	注意と制限
  Mdl	モデル オブジェクトの使用上の注意および制限については、incrementalClassificationLinear または incrementalRegressionLinear を参照してください。
  X	バッチ間の観測値の数は可変サイズにすることができますが、対応する Y の観測値の数と等しくなければなりません。 予測子変数の数は Mdl.NumPredictors と等しくなければなりません。 X は single または double でなければなりません。
  Y	バッチ間の観測値の数は可変サイズにすることができますが、対応する X の観測値の数と等しくなければなりません。 分類問題では、Y のすべてのラベルを Mdl.ClassNames で表さなければなりません。 Y と Mdl.ClassNames は同じデータ型でなければなりません。
  'LossFun'	指定する関数を無名関数にすることはできません。

• データをシャッフルするように Mdl を構成した場合 (Mdl.Shuffle が true であるか、Mdl.Solver が 'sgd' または 'asgd')、関数 loss は、モデルをバッチに当てはめる前に観測値の各入力バッチを無作為にシャッフルします。シャッフルされた観測値の順序は、MATLAB^® で生成される順序と一致しないことがあります。したがって、損失を計算する前に Mdl を当てはめた場合、MATLAB で計算される損失と生成コードで計算される損失が等しくならない場合があります。

• 浮動小数点の入力引数およびオブジェクト プロパティには、すべて同質なデータ型を使用します。具体的には、single または double のいずれかです。

詳細は、コード生成の紹介を参照してください。

バージョン履歴

R2020b で導入

R2022a: 欠損値がある予測子データに対して loss で NaN が返されることがある

関数 loss で加重平均損失を計算する際に、予測 (分類の場合はスコア、回帰の場合は応答) が NaN の観測値が省略されなくなりました。そのため、予測子データ X に欠損値があり、名前と値の引数 LossFun が "classiferror" (分類の場合) として指定されていない場合に、loss で NaN が返されることがあります。ほとんどの場合、データ セットに予測子の欠損がなければ、関数 loss で NaN が返されることはありません。

コードの loss で NaN が返される場合、このような結果にならないようにコードを更新できます。rmmissing または fillmissing を使用して、欠損値を削除するか置き換えます。

参考

オブジェクト

• incrementalClassificationLinear | incrementalRegressionLinear

関数

• updateMetrics | fit | updateMetricsAndFit | predict

トピック

• インクリメンタル学習の概要
• インクリメンタル学習モデルの構成