incrementalClassificationNaiveBayes

インクリメンタル学習用の単純ベイズ分類モデル

R2021a 以降

説明

関数 incrementalClassificationNaiveBayes は incrementalClassificationNaiveBayes モデル オブジェクトを作成します。これは、インクリメンタル学習用の単純ベイズ マルチクラス分類モデルを表します。

他の Statistics and Machine Learning Toolbox™ モデル オブジェクトとは異なり、incrementalClassificationNaiveBayes は直接呼び出すことができます。また、モデルをデータに当てはめる前に、パフォーマンス メトリクス構成やクラスの事前確率などの学習オプションを指定できます。incrementalClassificationNaiveBayes オブジェクトを作成すると、インクリメンタル学習用に準備されます。

incrementalClassificationNaiveBayes は、インクリメンタル学習に最適です。マルチクラス分類用の単純ベイズ モデルに学習させるための従来のアプローチ (データへの当てはめによるモデルの作成、交差検証の実行、ハイパーパラメーターの調整など) については、fitcnb を参照してください。

作成

incrementalClassificationNaiveBayes モデル オブジェクトは、次のいくつかの方法で作成できます。

• 関数の直接呼び出し — incrementalClassificationNaiveBayes を直接呼び出して、インクリメンタル学習オプションを構成するか、学習器固有のオプションを指定します。このアプローチは、データがまだない場合やインクリメンタル学習をすぐに開始したい場合に最適です。インクリメンタル学習中に応答データで予測される最大クラス数またはすべてのクラス名を指定しなければなりません。

• 従来式の学習済みモデルの変換 — 学習済みモデル オブジェクト (ClassificationNaiveBayes) のモデル パラメーターを使用して、インクリメンタル学習用の単純ベイズ分類モデルを初期化するには、従来式の学習済みモデルを関数 incrementalLearner に渡して incrementalClassificationNaiveBayes モデル オブジェクトに変換できます。

• インクリメンタル学習関数の呼び出し — fit、updateMetrics、および updateMetricsAndFit は、構成済みの incrementalClassificationNaiveBayes モデル オブジェクトおよびデータを入力として受け入れ、入力モデルとデータから学習した情報で更新された incrementalClassificationNaiveBayes モデル オブジェクトを返します。

構文

Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',MaxNumClasses)

Mdl = incrementalClassificationNaiveBayes('ClassNames',ClassNames)

Mdl = incrementalClassificationNaiveBayes(___,Name,Value)

説明

Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',MaxNumClasses) は、単純ベイズ分類用の既定のインクリメンタル学習モデル オブジェクト Mdl を返します。MaxNumClasses は、インクリメンタル学習中に応答データで予測される最大クラス数です。既定のモデルのプロパティには、未知のモデル パラメーター用のプレースホルダーが含まれています。既定のモデルは、パフォーマンスを追跡したり、予測を生成したりする前に学習させなければなりません。

Mdl = incrementalClassificationNaiveBayes('ClassNames',ClassNames) は、インクリメンタル学習中に応答データで予測されるすべてのクラス名 ClassNames を指定し、ClassNames プロパティを設定します。

Mdl = incrementalClassificationNaiveBayes(___,Name,Value) は、前の構文のいずれかを使用し、名前と値の引数を使用してプロパティと追加のオプションを設定します。それぞれの名前は引用符で囲みます。たとえば、incrementalClassificationNaiveBayes('DistributionNames','mn','MaxNumClasses',5,'MetricsWarmupPeriod',100) は、予測子変数の条件付き結合分布を多項に指定して、応答データで予測される最大クラス数を 5 に設定し、メトリクスのウォームアップ期間を 100 に設定します。

入力引数

MaxNumClasses — 最大クラス数

正の整数

インクリメンタル学習中に応答データで予測される最大クラス数。正の整数として指定します。

MaxNumClasses は ClassNames プロパティ内のクラス名の数を設定します。

MaxNumClasses を指定しない場合は、ClassNames 引数を指定しなければなりません。

例: 'MaxNumClasses',5

データ型: single | double

ClassNames — すべての一意のクラス ラベル

categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

インクリメンタル学習中に応答データで予測されるすべての一意のクラス ラベル。categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列として指定します。ClassNames と応答データは同じデータ型でなければなりません。この引数は ClassNames プロパティを設定します。

ClassNames は、クラスの順序に対応する入力または出力引数の次元の順序を指定します。たとえば、Cost の次元の順序や predict によって返される分類スコアの列の順序を指定するために 'ClassNames' を設定します。

ClassNames を指定しない場合は、MaxNumClasses 引数を指定しなければなりません。その場合、インクリメンタル学習中にデータから ClassNames プロパティが推定されます。

例: 'ClassNames',["virginica" "setosa" "versicolor"]

データ型: single | double | logical | string | char | cell | categorical

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'NumPredictors',4,'Prior',[0.3 0.3 0.4] は、予測子データ内の変数の個数 4 とクラスの事前確率分布 [0.3 0.3 0.4] を指定します。

Cost — 観測値を誤分類するコスト

正方行列 | 構造体配列

観測値を誤分類するコスト。次の表の値として指定します。ここで、c は ClassNames プロパティ内のクラスの数です。

値	説明
c 行 c 列の数値行列	Cost(i,j) は、クラス ClassNames(i) およびクラス ClassNames(j) に対して、真のクラスが i の場合に観測値をクラス j に分類するコストです。つまり、行は真のクラスに、列は予測するクラスに対応します。たとえば、Cost = [0 2;1 0] は、ClassNames(1) の誤分類に ClassNames(2) の誤分類の 2 倍のペナルティを適用します。
構造体配列	次の 2 つのフィールドをもつ構造体配列です。 ClassNames には、ClassNames と同じ値のクラス名が格納されます。 ClassificationCosts には、前述のコスト行列が格納されます。

Cost を指定する場合は、ClassNames 引数も指定しなければなりません。Cost は Cost プロパティを設定します。

既定は次のいずれかです。

• MaxNumClasses を指定した場合、空の配列 []

• ClassNames を指定した場合、c 行 c 列の行列。ここで、すべての i ≠ j に対しては Cost(i,j) = 1、すべての i = j に対しては Cost(i,j) = 0

例: 'Cost',struct('ClassNames',{'b','g'},'ClassificationCosts',[0 2; 1 0])

データ型: single | double | struct

Metrics — インクリメンタル学習中に追跡するモデルのパフォーマンス メトリクス

"mincost" (既定値) | "classiferror" | string ベクトル | 関数ハンドル | cell ベクトル | 構造体配列 | "binodeviance" | "exponential" | "hinge" | "logit" | "quadratic"

最小予測誤分類コストに加えてインクリメンタル学習中に追跡するモデルのパフォーマンス メトリクス。組み込みの損失関数の名前、名前の string ベクトル、関数ハンドル (@metricName など)、関数ハンドルの構造体配列、または名前、関数ハンドル、構造体配列の cell ベクトルとして指定します。

Mdl が "ウォーム" のとき (IsWarm を参照)、updateMetrics および updateMetricsAndFit は Mdl の Metrics プロパティのパフォーマンス メトリクスを追跡します。

次の表は、組み込みの損失関数名の一覧です。string ベクトルを使用して、複数指定できます。

名前	説明
"binodeviance"	二項分布からの逸脱度
"classiferror"	誤分類誤差率
"exponential"	指数
"hinge"	ヒンジ
"logit"	ロジスティック
"mincost"	最小予測誤分類コスト (事後確率である分類スコアの場合)。incrementalClassificationNaiveBayes は、このメトリクスを常に追跡します。
"quadratic"	2 次

組み込み損失関数の詳細については、loss を参照してください。

例: 'Metrics',["classiferror" "logit"]

パフォーマンス メトリクスを返すカスタム関数を指定するには、関数ハンドル表記を使用します。関数は次の形式でなければなりません。

metric = customMetric(C,S,Cost)

• 出力引数 metric は n 行 1 列の数値ベクトルです。ここで、各要素は、学習サイクル中にインクリメンタル学習関数によって処理されたデータの対応する観測値の損失です。

• 関数名 (ここでは customMetric) を指定します。

• C は n 行 K 列の logical 行列であり、対応する観測値が属するクラスを各行が示します。K はクラスの数です。列の順序は ClassNames プロパティのクラスの順序に対応します。C を作成するには、指定されたデータの各観測値について観測値 p がクラス q に属する場合に C(p,q) = 1 を設定します。行 p の他の要素を 0 に設定します。

• S は、予測分類スコアの n 行 K 列の数値行列です。S は predict の出力 Posterior に似ています。ここで、行はデータの観測値に対応し、列の順序は ClassNames プロパティのクラスの順序に対応しています。S(p,q) は、クラス q に分類されている観測値 p の分類スコアです。

• Cost は、誤分類コストの、K 行 K 列の数値行列です。名前と値の引数 'Cost' を参照してください。

複数のカスタム メトリクスを指定し、それぞれにカスタム名を割り当てるには、構造体配列を使用します。組み込みメトリクスとカスタム メトリクスの組み合わせを指定するには、cell ベクトルを使用します。

例: 'Metrics',struct('Metric1',@customMetric1,'Metric2',@customMetric2)

例: 'Metrics',{@customMetric1 @customMetric2 'logit' struct('Metric3',@customMetric3)}

updateMetrics および updateMetricsAndFit は、table で指定したメトリクスを Metrics プロパティに保存します。Metrics のデータ型によって、table の行名が決まります。

'Metrics' 値のデータ型	Metrics プロパティの行名の説明	例
string または文字ベクトル	対応する組み込みメトリクスの名前	"classiferror" の行名は "ClassificationError"
構造体配列	フィールド名	struct('Metric1',@customMetric1) の行名は "Metric1"
プログラム ファイルに格納されている関数への関数ハンドル	関数名	@customMetric の行名は "customMetric"
無名関数	CustomMetric_j。ここで、j は Metrics のメトリクス j	@(C,S,Cost)customMetric(C,S,Cost)... の行名は CustomMetric_1

パフォーマンス メトリクス オプションの詳細については、パフォーマンス メトリクスを参照してください。

データ型: char | string | struct | cell | function_handle

プロパティ

ほとんどのプロパティは、incrementalClassificationNaiveBayes を直接呼び出すときに名前と値のペアの引数の構文のみを使用して設定できます。incrementalLearner を呼び出して従来式の学習済みモデルを変換するときに、いくつかのプロパティを設定できます。プロパティ DistributionParameters、IsWarm、および NumTrainingObservations は設定できません。

分類モデルのパラメーター

CategoricalPredictors — カテゴリカル予測子のリスト

読み取り専用: 正の整数のベクトル | logical ベクトル | "all"

この プロパティ は読み取り専用です。

カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。

値	説明
正の整数のベクトル	ベクトルの各エントリは、カテゴリカル変数が含まれている予測子データの列に対応するインデックス値です。インデックス値の範囲は 1 ～ NumPredictors です。
logical ベクトル	true というエントリは、予測子データの対応する列がカテゴリカル変数であることを意味します。ベクトルの長さは NumPredictors です。
"all"	すべての予測子がカテゴリカルです。

特定されたカテゴリカル予測子に対して、incrementalClassificationNaiveBayes は多変量多項分布を使用します。詳細については、DistributionNames を参照してください。

既定では、DistributionNames オプションを指定した場合、'mvmn' に対応するすべての予測子変数は categorical です。そうでない場合、categorical である予測子変数はありません。

例: 'CategoricalPredictors',[1 2 4] および 'CategoricalPredictors',[true true false true] は、4 個の予測子変数のうち、1 番目、2 番目、4 番目を categorical に指定します。

データ型: single | double | logical

CategoricalLevels — 多変量多項予測子変数のレベル

cell ベクトル

多変量多項予測子変数のレベル。cell ベクトルとして指定します。CategoricalLevels の長さは NumPredictors と同じです。

インクリメンタル近似関数 fit および updateMetricsAndFit は cell に各カテゴリカル予測子変数の学習済み数値カテゴリカル レベルを挿入しますが、他の予測子変数に対応する cell には空の配列 [] が含まれます。特に、予測子 j が多変量多項の場合、CategoricalLevels{j} は、インクリメンタル当てはめ中に発生した予測子 j のすべての異なる値のリストです。詳細については、DistributionNames プロパティを参照してください。

メモ

fitcnb とは異なり、インクリメンタル近似関数は予測子のレベルを学習中に発生した順番に並べます。たとえば、予測子 j が多変量多項分布の categorical であるとします。CategoricalLevels{j} のレベルの順番、結果としてインクリメンタル近似関数によって返される DistributionParameters{:,j} の各 cell にあるレベル確率の順番は、同じ学習データ セットに対して fitcnb が返す順番と異なる場合があります。

Cost — 観測値を誤分類するコスト

読み取り専用: 正方数値行列 | 空の配列 []

この プロパティ は読み取り専用です。

観測値を誤分類するコスト。配列として指定します。

名前と値の引数 'Cost' を指定した場合、その値で Cost が設定されます。構造体配列を指定した場合は、Cost は ClassificationCosts フィールドの値になります。

従来式の学習済みモデルを変換して Mdl を作成する場合、Cost は従来式の学習済みモデルの Cost プロパティです。

データ型: single | double

ClassNames — すべての一意のクラス ラベル

読み取り専用: categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

この プロパティ は読み取り専用です。

インクリメンタル学習中に応答データで予測されるすべての一意のクラス ラベル。categorical 配列、文字配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列として指定します。

ClassNames は次の 3 つのいずれかの方法で設定できます。

• MaxNumClasses 引数を指定した場合、インクリメンタル学習中に ClassNames プロパティが推定されます。

• ClassNames 引数を指定した場合、incrementalClassificationNaiveBayes はその指定を ClassNames プロパティに格納します。(string 配列は文字ベクトルの cell 配列として扱われます)。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、ClassNames プロパティは従来式の学習済みモデルの対応するプロパティによって指定されます。

データ型: single | double | logical | char | string | cell | categorical

NumPredictors — 予測子変数の数

読み取り専用: 非負の数値スカラー

この プロパティ は読み取り専用です。

予測子変数の数。非負の数値スカラーとして指定します。

NumPredictors の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、NumPredictors は従来式の学習済みモデルの対応するプロパティによって指定されます。

• incrementalClassificationNaiveBayes を直接呼び出して Mdl を作成する場合、NumPredictors は名前と値の引数の構文を使用して指定できます。値を指定しない場合、既定値は 0 で、インクリメンタル近似関数は学習中に予測子データから NumPredictors を推測します。

データ型: double

NumTrainingObservations — インクリメンタル モデルに当てはめる観測値の数

読み取り専用: 0 (既定値) | 非負の数値スカラー

この プロパティ は読み取り専用です。

インクリメンタル モデル Mdl に当てはめる観測値の数。非負の数値スカラーとして指定します。NumTrainingObservations は、Mdl および学習データを fit または updateMetricsAndFit に渡すときに増加します。

メモ

従来式の学習済みモデルを変換して Mdl を作成する場合、incrementalClassificationNaiveBayes は、従来式の学習済みモデルに当てはめる観測値の数を NumTrainingObservations に追加しません。

データ型: double

Prior — 事前クラス確率

読み取り専用: 数値ベクトル | 'empirical' | 'uniform'

この プロパティ は読み取り専用です。

クラスの事前確率。'empirical'、'uniform'、または数値ベクトルとして指定します。incrementalClassificationNaiveBayes は Prior 値を数値ベクトルとして格納します。

値	説明
'empirical'	インクリメンタル学習関数が、インクリメンタル学習中に応答データで観測されたクラスの相対頻度から前のクラスの確率を推定します。
'uniform'	各クラスの事前確率を 1/K とします。ここで、K はクラスの数です。
数値ベクトル	正規化されたカスタム事前確率。Prior の要素の順序は ClassNames プロパティの要素に対応します。

Prior の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、Prior は従来式の学習済みモデルの対応するプロパティによって指定されます。

• それ以外の場合、Prior の既定値は 'empirical' です。

データ型: single | double | char | string

ScoreTransform — スコア変換関数

読み取り専用: 'none' (既定値) | string スカラー | 文字ベクトル | 関数ハンドル

この プロパティ は読み取り専用です。

インクリメンタル変換関数が生の応答値を変換する方法を記述するスコア変換関数。文字ベクトル、string スカラー、または関数ハンドルとして指定します。incrementalClassificationNaiveBayes は、指定された値を文字ベクトルまたは関数ハンドルとして格納します。

次の表は、スコア変換で使用可能な組み込み関数の一覧です。

値	説明
"doublelogit"	1/(1 + e–2x)
"invlogit"	log(x / (1 – x))
"ismax"	最大のスコアをもつクラスのスコアを 1 に設定し、他のすべてのクラスのスコアを 0 に設定する
"logit"	1/(1 + e–x)
"none" または "identity"	x (変換なし)
"sign"	x < 0 のとき –1 x = 0 のとき 0 x > 0 のとき 1
"symmetric"	2x – 1
"symmetricismax"	最大のスコアをもつクラスのスコアを 1 に設定し、他のすべてのクラスのスコアを –1 に設定する
"symmetriclogit"	2/(1 + e–x) – 1

MATLAB^® 関数やユーザー定義関数の場合は、関数ハンドルを入力します。たとえば、@function では次のようになります。

• function は n 行 K 列の行列 (元のスコア) を受け入れ、同じサイズの行列 (変換されたスコア) を返します。

• n は観測値の数であり、行列の行 j には、観測値 j のクラス スコアが格納されます。

• K クラスの数で、列 k はクラス ClassNames(k) です。

ScoreTransform の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、ScoreTransform は従来式の学習済みモデルの対応するプロパティによって指定されます。

• 既定の 'none' は、事後クラス確率を返すことを指定します。

データ型: char | function_handle | string

学習パラメーター

DistributionNames — 予測子分布

"mn" | "mvmn" | "normal" | string ベクトル | 文字ベクトルの cell ベクトル

予測子分布 P(x|c_k)。ここで、c_k はクラス ClassNames(k) です。文字ベクトル、string スカラー、1 行 NumPredictors 列の string ベクトル、または次の表の値をもつ文字ベクトルの cell ベクトルとして指定します。

値	説明
"mn"	多項分布。"mn" を指定すると、すべての特徴量は多項分布の成分となります (たとえば、bag-of-tokens モデル)。したがって、"mn" を文字ベクトルの cell 配列または string 配列の要素として含めることはできません。詳細については、多項分布の推定確率を参照してください。
"mvmn"	多変量多項分布。詳細については、多変量多項分布の推定確率を参照してください。
"normal"	正規分布。詳細については、正規分布の推定器を参照してください。

文字ベクトルまたは string スカラーを指定した場合、その分布を使用してすべての特徴量がモデル化されます。1 行 NumPredictors 列の string ベクトルまたは文字ベクトルの cell ベクトルを指定した場合、ベクトルの要素 "j" の分布を使用して特徴量 "j" がモデル化されます。

既定では、カテゴリカル予測子として指定されたすべての予測子は (CategoricalPredictors プロパティを参照) 'mvmn' に設定されます。それ以外の場合、既定の分布は 'normal' となります。

incrementalClassificationNaiveBayes は、値を文字ベクトル、または文字ベクトルの cell ベクトルとして格納します。

例: 'DistributionNames',"mn" は、すべての予測子変数の条件付き結合分布を多項に指定します。

例: 'DistributionNames',["normal" "mvmn" "normal"] は、1 番目と 3 番目の予測子変数を正規分布に、2 番目の変数を多変量多項分布をもつ categorical に指定します。

データ型: char | string | cell

DistributionParameters — 分布パラメーターの推定

読み取り専用: cell 配列

この プロパティ は読み取り専用です。

分布パラメーターの推定。cell 配列として指定します。DistributionParameters は K 行 NumPredictors 列の cell 配列です。ここで、K はクラスの数であり、セル (k,j) はクラス k における予測子 j のインスタンスを推定した分布パラメーターを含みます。行の順序は ClassNames プロパティのクラスの順序に対応し、列の順序は予測子データの予測子の順序に対応します。

クラス k に予測子 j の観測値がない場合、DistributionParameters{k,j} は空 ([]) です。

DistributionParameters の要素は予測子の分布に依存します。次の表は、DistributionParameters{k,j} の値について説明しています。

予測子 j の分布	予測子 j およびクラス k の cell 配列の値
'mn'	トークン j がクラス k に出現する確率を表すスカラー。詳細については、多項分布の推定確率を参照してください。
'mvmn'	クラス k の予測子 j の可能なレベルそれぞれの確率を含む数値ベクトル確率は予測子 j (プロパティ CategoricalLevels 内に格納されています) のすべての一意なレベルが並べ替えられた順序に並べられます。詳細については、多変量多項分布の推定確率を参照してください。
'normal'	2 行 1 列の数値ベクトル。最初の要素は重み付き標本平均で、2 番目の要素は重み付き標本標準偏差です。詳細については、正規分布の推定器を参照してください。

メモ

fitcnb とは異なり、インクリメンタル近似関数は予測子のレベルを学習中に発生した順番に並べます。たとえば、予測子 j が多変量多項分布の categorical であるとします。CategoricalLevels{j} のレベルの順番、結果としてインクリメンタル近似関数によって返される DistributionParameters{:,j} の各 cell にあるレベル確率の順番は、同じ学習データ セットに対して fitcnb が返す順番と異なる場合があります。

データ型: cell

パフォーマンス メトリクス パラメーター

IsWarm — モデルがパフォーマンス メトリクスを追跡するかどうかを示すフラグ

false または 0 | true または 1

インクリメンタル モデルがパフォーマンス メトリクスを追跡するかどうかを示すフラグ。logical 0 (false) または 1 (true) として指定します。

インクリメンタル モデル Mdl は、インクリメンタル近似関数で次の両方のアクションを実行すると "ウォーム" (IsWarm が true) になります。

• インクリメンタル モデルを MetricsWarmupPeriod の観測値に当てはめる。

• MaxNumClasses のクラス、または名前と値の引数 ClassNames で指定されたすべてのクラス名を処理する。

値	説明
true または 1	インクリメンタル モデル Mdl がウォームです。この結果、updateMetrics および updateMetricsAndFit が Mdl の Metrics プロパティのパフォーマンス メトリクスを追跡します。
false または 0	updateMetrics および updateMetricsAndFit はパフォーマンス メトリクスを追跡しません。

データ型: logical

Metrics — モデルのパフォーマンス メトリクス

読み取り専用: table

この プロパティ は読み取り専用です。

updateMetrics および updateMetricsAndFit によってインクリメンタル学習中に更新されたモデルのパフォーマンス メトリクス。m 行 2 列の table として指定します。ここで、m は、名前と値の引数 Metrics によって指定されたメトリクスの数です。

Metrics の列には Cumulative および Window のラベルが付けられます。

• Cumulative:要素 j は、メトリクス j で測定される、モデルがウォーム (IsWarm が 1) になった時点からの、モデルの性能です。

• Window:要素 j は、メトリクス j で測定され、MetricsWindowSize プロパティで指定されたウィンドウ内のすべての観測値に対して評価される、モデルの性能です。ソフトウェアは MetricsWindowSize 個の観測値を処理した後、Window を更新します。

行には、指定したメトリクスのラベルが付けられます。詳細については、incrementalLearner または incrementalClassificationNaiveBayes の名前と値の引数 Metrics を参照してください。

データ型: table

MetricsWarmupPeriod — パフォーマンス メトリクスを追跡する前に当てはめる観測値の数

読み取り専用: 非負の整数

この プロパティ は読み取り専用です。

インクリメンタル モデルが Metrics プロパティのパフォーマンス メトリクスを追跡する前に当てはめなければならない観測値の数。非負の整数として指定します。

MetricsWarmupPeriod の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 MetricsWarmupPeriod で行います。この引数の既定値は 0 です。

• それ以外の場合、既定値は 1000 です。

詳細については、パフォーマンス メトリクスを参照してください。

データ型: single | double

MetricsWindowSize — ウィンドウ パフォーマンス メトリクスの計算に使用する観測値の数

読み取り専用: 正の整数

この プロパティ は読み取り専用です。

ウィンドウ パフォーマンス メトリクスの計算に使用する観測値の数。正の整数として指定します。

MetricsWindowSize の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 MetricsWindowSize で行います。この引数の既定値は 200 です。

• それ以外の場合、既定値は 200 です。

パフォーマンス メトリクス オプションの詳細については、パフォーマンス メトリクスを参照してください。

データ型: single | double

オブジェクト関数

fit	インクリメンタル学習用の単純ベイズ分類モデルの学習
updateMetricsAndFit	単純ベイズ インクリメンタル学習分類モデルの新しいデータに基づくパフォーマンス メトリクスの更新とモデルの学習
updateMetrics	単純ベイズ インクリメンタル学習分類モデルの新しいデータに基づくパフォーマンス メトリクスの更新
logp	インクリメンタル学習用の単純ベイズ分類モデルの対数条件なし確率密度
loss	データのバッチでの単純ベイズ インクリメンタル学習分類モデルの損失
predict	単純ベイズ インクリメンタル学習分類モデルからの新しい観測値の応答予測
perObservationLoss	インクリメンタル学習用モデルの観測値ごとの分類誤差
reset	インクリメンタル分類モデルのリセット

例

十分な事前情報なしでのインクリメンタル学習器の作成

インクリメンタル学習用の単純ベイズ分類モデルを作成するには、モデルが処理する、予測される最大クラス数 (名前と値の引数 'MaxNumClasses') を指定する必要があります。インクリメンタル近似関数を使用してデータの入力バッチにモデルを当てはめると、モデルで新しいクラスが ClassNames プロパティに収集されます。最大クラス数の指定が正確でないと、次のいずれかが発生します。

• 予測される最大クラス数をインクリメンタル近似関数が処理するまで、モデルはコールドになります。その結果、関数 updateMetrics および updateMetricsAndFit でパフォーマンス メトリクスが測定されません。

• 予測される最大数をクラスの数が超えると、インクリメンタル近似関数でエラーが発行されます。

この例では、データに含まれる予測される最大クラス数しか情報を指定しない場合の、インクリメンタル学習用単純ベイズ分類モデルの作成方法を示します。また、インクリメンタル近似関数が標本の早い時点と遅い時点のすべての予測されるクラスを処理する場合の結果も示します。

この例では、デバイスに学習させ、被験者で測定された生体データに基づいて、被験者が座る、立つ、歩く、走る、踊るのいずれの状態であるかを予測するとします。したがって、デバイスが選択することになるクラスは最大 5 つです。

予測される最大クラス数を標本の早い時点で処理

マルチクラス学習用のインクリメンタル単純ベイズ モデルを作成します。データ内のクラスの最大数を 5 と指定します。

MdlEarly = incrementalClassificationNaiveBayes('MaxNumClasses',5)

MdlEarly = 
  incrementalClassificationNaiveBayes

                    IsWarm: 0
                   Metrics: [1×2 table]
                ClassNames: [1×0 double]
            ScoreTransform: 'none'
         DistributionNames: 'normal'
    DistributionParameters: {}


  Properties, Methods

MdlEarly は incrementalClassificationNaiveBayes モデル オブジェクトです。そのプロパティはすべて読み取り専用です。

MdlEarly は、他の演算の実行に使用する前に、データに当てはめなければなりません。

人の行動のデータ セットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1); % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データ セットの詳細については、コマンド ラインで Description を入力してください。

関数 updateMetricsAndFit を使用して、インクリメンタル モデルを学習データに当てはめます。50 個の観測値のチャンクを一度に処理して、データ ストリームをシミュレートします。各反復で次を行います。

• 50 個の観測値を処理します。

• 前のインクリメンタル モデルを、入力観測値に当てはめた新しいモデルで上書きします。

• 1 番目のクラス内の 1 番目の予測子の平均 ${\mu }_{11}$、累積メトリクス、およびウィンドウ メトリクスを保存し、インクリメンタル学習中にそれらがどのように進化するかを確認します。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
mc = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
mu1 = zeros(nchunk+1,1);    

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    MdlEarly = updateMetricsAndFit(MdlEarly,X(idx,:),Y(idx));
    mc{j,:} = MdlEarly.Metrics{"MinimalCost",:};
    mu1(j + 1) = MdlEarly.DistributionParameters{1,1}(1);
end

MdlEarly は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデル オブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetricsAndFit は入力観測値でモデルの性能をチェックし、モデルをその観測値に当てはめます。

パフォーマンス メトリクスと ${\mu }_{11}$ が学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(mu1)
ylabel('\mu_{11}')
xlim([0 nchunk])
nexttile
h = plot(mc.Variables);
xlim([0 nchunk])
ylabel('Minimal Cost')
xline(MdlEarly.MetricsWarmupPeriod/numObsPerChunk,'r-.')
legend(h,mc.Properties.VariableNames)
xlabel(t,'Iteration')

このプロットは、updateMetricsAndFit が次のアクションを実行することを示しています。

• ${\mu }_{11}$ をインクリメンタル学習のすべての反復で当てはめます。

• パフォーマンス メトリクスをメトリクスのウォームアップ期間 (赤色の垂直な線) 後にのみ計算します。

• 累積メトリクスを各反復中に計算します。

• ウィンドウ メトリクスを 200 個の観測値 (4 回の反復) の処理後に計算します。

予測される最大クラス数を標本の遅い時点で処理

目的に合わせて、インクリメンタル学習用に別の単純ベイズ モデルを作成します。

MdlLate = incrementalClassificationNaiveBayes('MaxNumClasses',5)

MdlLate = 
  incrementalClassificationNaiveBayes

                    IsWarm: 0
                   Metrics: [1×2 table]
                ClassNames: [1×0 double]
            ScoreTransform: 'none'
         DistributionNames: 'normal'
    DistributionParameters: {}


  Properties, Methods

クラス 5 でラベル付けされたすべての観測値を標本の最後に移動します。

idx5 = Y == 5;
Xnew = [X(~idx5,:); X(idx5,:)];
Ynew = [Y(~idx5) ;Y(idx5)];

インクリメンタル モデルを当てはめて結果をプロットします。

mcnew = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
mu1new = zeros(nchunk,1);    

for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    MdlLate = updateMetricsAndFit(MdlLate,Xnew(idx,:),Ynew(idx));
    mcnew{j,:} = MdlLate.Metrics{"MinimalCost",:};
    mu1new(j + 1) = MdlLate.DistributionParameters{1,1}(1);
end

t = tiledlayout(2,1);
nexttile
plot(mu1new)
ylabel('\mu_{11}')
xlim([0 nchunk])
nexttile
h = plot(mcnew.Variables);
xlim([0 nchunk]);
ylabel('Minimal Cost')
xline(MdlLate.MetricsWarmupPeriod/numObsPerChunk,'r-.')
xline(sum(~idx5)/numObsPerChunk,'g-.')
legend(h,mcnew.Properties.VariableNames,'Location','best')
xlabel(t,'Iteration')

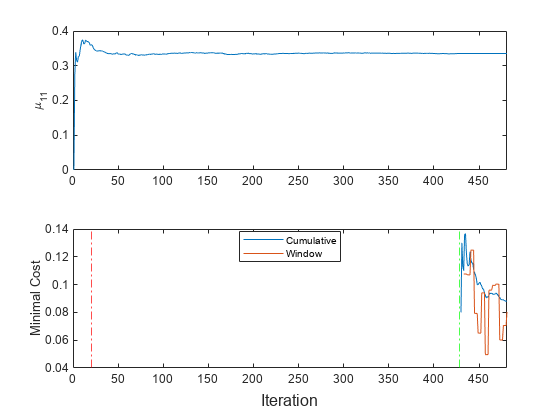
関数 updateMetricsAndFit は、インクリメンタル学習全体を通してモデルに学習させますが、予測されるすべてのクラスにモデルが当てはめられて初めて (下のタイルで緑色の垂直な線)、パフォーマンス メトリクスの追跡を開始します。

すべてのクラス名の指定

データに含まれるすべてのクラス名がわかっている場合にインクリメンタル単純ベイズ モデルを作成します。

デバイスに学習させ、被験者で測定された生体データに基づいて、被験者が座る、立つ、歩く、走る、踊るのいずれの状態であるかを予測するとします。各行動にはクラス名 1 ～ 5 をマッピングします。

マルチクラス学習用のインクリメンタル単純ベイズ モデルを作成します。クラス名を指定します。

classnames = 1:5;
Mdl = incrementalClassificationNaiveBayes('ClassNames',classnames)

Mdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 0
                   Metrics: [1×2 table]
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
         DistributionNames: 'normal'
    DistributionParameters: {5×0 cell}


  Properties, Methods

Mdl は incrementalClassificationNaiveBayes モデル オブジェクトです。そのプロパティはすべて読み取り専用です。

Mdl は、他の演算の実行に使用する前に、データに当てはめなければなりません。

人の行動のデータ セットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1); % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データ セットの詳細については、コマンド ラインで Description を入力してください。

関数 updateMetricsAndFit を使用して、インクリメンタル モデルを学習データに当てはめます。50 個の観測値のチャンクを一度に処理して、データ ストリームをシミュレートします。各反復で次を行います。

• 50 個の観測値を処理します。

• 前のインクリメンタル モデルを、入力観測値に当てはめた新しいモデルで上書きします。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,X(idx,:),Y(idx));
end

インクリメンタル学習オプションの構成

クラス名の最大数の指定に加え、メトリクスのウォームアップ期間を指定して、インクリメンタル単純ベイズ学習器を準備します。その間、関数 updateMetricsAndFit はモデルの当てはめのみを行います。メトリクス ウィンドウ サイズを観測値 500 個に指定します。

人の行動のデータ セットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1); % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

被験者で測定された生体データに基づいて、座る、立つ、歩く、走る、踊るの各行動に、クラス名 1 ～ 5 をマッピングします。データ セットの詳細については、コマンド ラインで Description を入力してください。

マルチクラス学習用のインクリメンタル単純ベイズ モデルを作成します。次のようにモデルを構成します。

• メトリクスのウォームアップ期間を観測値 5000 個に指定します。

• メトリクス ウィンドウ サイズを観測値 500 個に指定します。

• クラス 2 を誤分類した場合は、分類器に 2 倍のペナルティを与える。

• 分類誤差および最小コストを追跡してモデルの性能を測定。incrementalClassificationNaiveBayes はこのメトリクスを常に追跡するため、Metrics に 'mincost' を指定する必要はありません。

C = ones(5) - eye(5);
C(2,[1 3 4 5]) = 2;
Mdl = incrementalClassificationNaiveBayes('ClassNames',1:5, ...
    'MetricsWarmupPeriod',5000,'MetricsWindowSize',500, ...
    'Cost',C,'Metrics','classiferror')

Mdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 0
                   Metrics: [2×2 table]
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
         DistributionNames: 'normal'
    DistributionParameters: {5×0 cell}


  Properties, Methods

Mdl はインクリメンタル学習用に構成された incrementalClassificationNaiveBayes モデル オブジェクトです。

関数 updateMetricsAndFit を使用して、インクリメンタル モデルを残りのデータに当てはめます。各反復で次を行います。

• 50 個の観測値のチャンクを処理して、データ ストリームをシミュレートします。

• 前のインクリメンタル モデルを、入力観測値に当てはめた新しいモデルで上書きします。

• 1 番目のクラス内の 1 番目の予測子変数の標準偏差 ${\sigma }_{11}$、累積メトリクス、およびウィンドウ メトリクスを保存し、インクリメンタル学習中にそれらがどのように進化するかを確認。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ce = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
mc = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
sigma11 = zeros(nchunk+1,1);    

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,X(idx,:),Y(idx));
    ce{j,:} = Mdl.Metrics{"ClassificationError",:};
    mc{j,:} = Mdl.Metrics{"MinimalCost",:};
    sigma11(j + 1) = Mdl.DistributionParameters{1,1}(2);
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデル オブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetricsAndFit は入力観測値でモデルの性能をチェックし、モデルをその観測値に当てはめます。

パフォーマンス メトリクスと ${\sigma }_{11}$ が学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

tiledlayout(2,2)
nexttile
plot(sigma11)
ylabel('\sigma_{11}')
xlim([0 nchunk]);
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.')
xlabel('Iteration')
nexttile
h = plot(ce.Variables);
xlim([0 nchunk])
ylabel('Classification Error')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.')
legend(h,ce.Properties.VariableNames)
xlabel('Iteration')
nexttile
h = plot(mc.Variables);
xlim([0 nchunk]);
ylabel('Minimal Cost')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.')
legend(h,mc.Properties.VariableNames)
xlabel('Iteration')

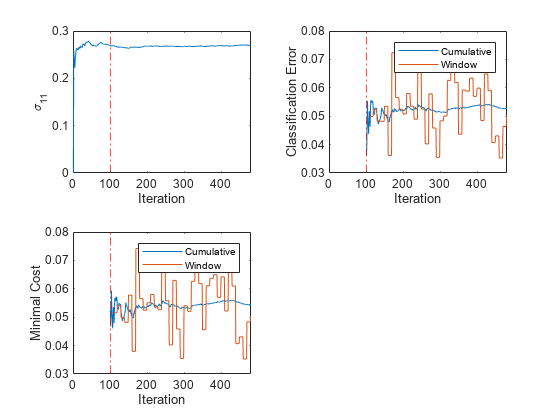
このプロットは、updateMetricsAndFit が次のアクションを実行することを示しています。

• ${\sigma }_{11}$ をインクリメンタル学習のすべての反復で当てはめます。

• パフォーマンス メトリクスをメトリクスのウォームアップ期間 (赤色の垂直な線) 後にのみ計算します。

• 累積メトリクスを各反復中に計算します。

• ウィンドウ メトリクスを 500 個の観測値 (10 回の反復) の処理後に計算します。

従来式の学習済みモデルのインクリメンタル学習器への変換

fitcnb を使用して、マルチクラス分類用の単純ベイズ モデルに学習させます。次に、そのモデルをインクリメンタル学習器に変換し、その性能を追跡し、モデルをストリーミング データに当てはめます。学習オプションを従来式からインクリメンタル学習に引き継ぎます。

データの読み込みと前処理

人の行動のデータ セットを読み込みます。データをランダムにシャッフルします。

load humanactivity
rng(1) % For reproducibility
n = numel(actid);
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データ セットの詳細については、コマンド ラインで Description を入力してください。

被験者がアイドル (Y <= 2) だったときの収集データが、被験者が移動していたときのデータの倍の品質であると仮定します。アイドルの被験者から収集した観測値に 2 を割り当て、移動している被験者から収集した観測値に 1 を割り当てる重み変数を作成します。

W = ones(n,1) + (Y <= 2);

単純ベイズ モデルの学習

マルチクラス分類用の単純ベイズ モデルをデータの半分の無作為標本に当てはめます。

idxtt = randsample([true false],n,true);
TTMdl = fitcnb(X(idxtt,:),Y(idxtt),'Weights',W(idxtt))

TTMdl = 
  ClassificationNaiveBayes
              ResponseName: 'Y'
     CategoricalPredictors: []
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
           NumObservations: 12053
         DistributionNames: {1×60 cell}
    DistributionParameters: {5×60 cell}


  Properties, Methods

TTMdl は従来式の学習済み単純ベイズ モデルを表す ClassificationNaiveBayes モデル オブジェクトです。

学習済みモデルの変換

従来式の学習済み単純ベイズ モデルをインクリメンタル学習用の単純ベイズ分類モデルに変換します。

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 1
                   Metrics: [1×2 table]
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
         DistributionNames: {1×60 cell}
    DistributionParameters: {5×60 cell}


  Properties, Methods

パフォーマンス メトリクスの追跡とモデルの当てはめの個別の実行

関数 updateMetrics および fit を使用して、残りのデータに対してインクリメンタル学習を実行します。50 個の観測値を一度に処理して、データ ストリームをシミュレートします。各反復で次を行います。

1. updateMetrics を呼び出し、観測値の入力チャンクを所与として、モデルの分類誤差の累積とウィンドウを更新します。前のインクリメンタル モデルを上書きして、Metrics プロパティ内の損失を更新します。関数がモデルをデータ チャンクに当てはめないことに注意してください。チャンクはモデルに対して "新しい" データです。観測値の重みを指定します。

2. fit を呼び出して、観測値の入力チャンクにモデルを当てはめます。前のインクリメンタル モデルを上書きして、モデル パラメーターを更新します。観測値の重みを指定します。

3. 1 番目のクラスの 1 番目の予測子変数の最小コストと平均 ${\mu }_{11}$ を保存します。

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 50;
nchunk = floor(nil/numObsPerChunk);
mc = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
mu11 = [IncrementalMdl.DistributionParameters{1,1}(1); zeros(nchunk+1,1)];
Xil = X(idxil,:);
Yil = Y(idxil);
Wil = W(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx), ...
        'Weights',Wil(idx));
    mc{j,:} = IncrementalMdl.Metrics{"MinimalCost",:};
    IncrementalMdl = fit(IncrementalMdl,Xil(idx,:),Yil(idx),'Weights',Wil(idx));
    mu11(j+1) = IncrementalMdl.DistributionParameters{1,1}(1);
end

IncrementalMdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデル オブジェクトです。

あるいは、updateMetricsAndFit を使用して、新しいデータ チャンクに対するモデルのパフォーマンス メトリクスを更新し、モデルをデータに当てはめることもできます。

パフォーマンス メトリクスと ${\mu }_{11}$ のトレース プロットをプロットします。

t = tiledlayout(2,1);
nexttile
h = plot(mc.Variables);
xlim([0 nchunk])
ylabel('Minimal Cost')
legend(h,mc.Properties.VariableNames)
nexttile
plot(mu11)
ylabel('\mu_{11}')
xlim([0 nchunk])
xlabel(t,'Iteration')

累積の損失はすぐに平坦になり安定していますが、ウィンドウの損失には学習全体を通じて急な変動があります。

${\mu }_{11}$ はまず急激に変動した後、fit がより多くのチャンクを処理するにつれて徐々に平坦になります。

詳細

bag-of-tokens モデル

bag-of-tokens モデルでは、予測子 j の値は観測値のトークン j の発生数を表す非負の数値です。この多項モデルのカテゴリ (ビン) の数は、異なるトークンの数 (予測子の数) です。

インクリメンタル学習

"インクリメンタル学習" ("オンライン学習") は、予測子変数の分布、予測関数や目的関数の素性 (調整パラメーターの値を含む)、観測値にラベル付けがされているか等についてほぼ知識が無い時に、データ ストリームから入ってくるデータを処理することに関係している機械学習の一分野です。従来の機械学習は、モデルへの当てはめに十分にラベル付けされたデータを使用でき、交差検証を実施してハイパーパラメーターを調整し、予測子の分布を推論するもので、インクリメンタル学習と異なります。

入力観測値に対し、インクリメンタル学習モデルは、次のいずれかの方法 (通常はこの順序) でデータを処理します。

• ラベルを予測します。

• 予測性能を測定します。

• モデルの構造的な破綻やドリフトについてチェックします。

• 入力観測値へモデルを当てはめます。

詳細については、インクリメンタル学習の概要を参照してください。

アルゴリズム

パフォーマンス メトリクス

• 関数 updateMetrics および updateMetricsAndFit は、インクリメンタル モデルが "ウォーム" (IsWarm プロパティが true) のときにのみ、新しいデータからモデルのパフォーマンス メトリクス (Metrics) を追跡します。

  • incrementalLearner を使用してインクリメンタル モデルを作成するときに、MetricsWarmupPeriod が 0 (incrementalLearner の既定値) である場合、モデルは作成時にウォームになります。

  • それ以外の場合、インクリメンタル モデルは、fit または updateMetricsAndFit で次の両方のアクションを実行するとウォームになります。

    • インクリメンタル モデルを MetricsWarmupPeriod の観測値 ("メトリクスのウォームアップ期間") に当てはめる。

    • インクリメンタル モデルを予測されるすべてのクラスに当てはめる (incrementalClassificationNaiveBayes の引数 MaxNumClasses と ClassNames を参照)。

• インクリメンタル モデルの Metrics プロパティは、各パフォーマンス メトリクスの 2 つの形式を table の変数 (列) Cumulative および Window とし、個々のメトリクスを行に格納します。インクリメンタル モデルがウォームになると、updateMetrics および updateMetricsAndFit は次の頻度でメトリクスを更新します。

  • Cumulative — 関数は、モデルの性能追跡の開始以降の累積メトリクスを計算します。関数は、関数が呼び出されるたびにメトリクスを更新し、提供されたデータ セット全体に基づいて計算を行います。

  • Window — 関数は、名前と値の引数 MetricsWindowSize によって決定されたウィンドウ内のすべての観測値に基づいてメトリクスを計算します。MetricsWindowSize によってソフトウェアが Window メトリクスを更新する頻度も決まります。たとえば、MetricsWindowSize が 20 の場合、関数は提供されたデータの最後の 20 個の観測値に基づいてメトリクスを計算します (X((end – 20 + 1):end,:) および Y((end – 20 + 1):end))。

    ウィンドウ内のパフォーマンス メトリクスを追跡するインクリメンタル関数は、次のプロセスを使用します。

    1. 指定された各メトリクスについて長さ MetricsWindowSize のバッファーを保存し、観測値の重みのバッファーを保存します。

    2. 入力観測値のバッチに基づくモデル性能をメトリクス バッファーの要素に入力し、対応する観測値の重みを重みバッファーに格納します。

    3. バッファーがいっぱいになると、Mdl.Metrics.Window をメトリクス ウィンドウの性能の加重平均で上書きします。関数が観測値のバッチを処理するときにバッファーがあふれる場合、最新の入力観測値 MetricsWindowSize がバッファーに入り、最も古い観測値がバッファーから削除されます。たとえば、MetricsWindowSize が 20 で、メトリクス バッファーには前に処理されたバッチからの 10 個の値が存在し、15 個の値が入力されるとします。長さ 20 のウィンドウを構成するため、関数は 15 個の入力観測値からの測定値と前のバッチからの最新の 5 個の測定値を使用します。

• Cumulative と Window のパフォーマンス メトリクスの値を計算する際、スコアが NaN の観測値は省略されます。

正規分布の推定器

予測子変数 j が条件付き正規分布をもつ場合 (DistributionNames プロパティを参照)、クラス固有の加重平均、および加重標準偏差の偏った (最尤) 推定を計算することにより、この分布がデータに当てはめられます。各クラス k に対して以下を実行します。

• 予測子 j の加重平均は次のようになります。

  $${\overline{x}}_{j|k}=\frac{{\displaystyle \sum _{\{i:y_i=k\}}{w}_i{x}_{ij}}}{{\displaystyle \sum _{\{i:y_i=k\}}{w}_i}},$$

  ここで w_i は観測値 i の重みです。クラス内の重みは、その合計がクラスの事前確率になるように正規化されます。

• 予測子 j の加重標準偏差の不偏推定器は次のようになります。

  $$s_{j|k}={\left[\frac{{\displaystyle \sum _{\{i:y_i=k\}}{w}_i{\left(x_{ij}-{\overline{x}}_{j|k}\right)}^2}}{{\displaystyle \sum _{\{i:y_i=k\}}{w}_i}}\right]}^{1/2}.$$

多項分布の推定確率

すべての予測子変数が条件付き多項分布を構成する場合 (DistributionNames プロパティを参照)、bag-of-tokens モデルを使用して、この分布が当てはめられます。トークン j がプロパティ DistributionParameters{k,j} のクラス k に出現する確率が保存されます。加法平滑化[1]を使用すると、推定確率は次のようになります。

$$P(\text{token }j|\text{class }k)=\frac{1+c_{j|k}}{P+c_k},$$

ここで、以下になります。

• $$c_{j|k}=n_k\frac{{\displaystyle \sum _{\{i:y_i=k\}}^{}{x}_{ij}}{w}_i^{}}{{\displaystyle \sum _{\{i:y_i=k\}}^{}{w}_i}},$$ はクラス k におけるトークン j の重み付き発生数です。

• n_k はクラス k 内の観測数です。

• $$w_i^{}$$ は観測値 i の重みです。クラス内の重みは、その合計がクラスの事前確率になるように正規化されます。

• $$c_k={\displaystyle \sum _{j=1}^P{c}_{j|k}},$$ は、クラス k に含まれているすべてのトークンの重み付き発生数の合計です。

多変量多項分布の推定確率

予測子変数 j が条件付き多変量多項分布をもつ場合 (DistributionNames プロパティを参照)、次のような手順になります。

1. 一意のレベルのリストが収集され、並べ替えられたリストは CategoricalLevels に保存され、各レベルはビンと見なされます。予測子とクラスの各組み合わせは、個別の独立した多項確率変数です。

2. 各クラス k に対して、CategoricalLevels{j} に保存されたリストを使用して、カテゴリカル レベルごとのインスタンスがカウントされます。

3. クラス k の予測子 j が、プロパティ DistributionParameters{k,j} においてレベル L をもつ場合、すべてのレベルの確率は CategoricalLevels{j} に保存されます。加法平滑化[1]を使用すると、推定確率は次のようになります。

   $$P\left(\text{predictor }j=L|\text{class }k\right)=\frac{1+m_{j|k}(L)}{m_j+m_k},$$

   ここで、以下になります。

   • $$m_{j|k}(L)=n_k\frac{{\displaystyle \sum _{\{i:y_i=k\}}^{}I\{x_{ij}=L\}{w}_i^{}}}{{\displaystyle \sum _{\{i:y_i=k\}}^{}{w}_i^{}}},$$ は、クラス k 内の予測子 j が L に等しい観測値の重み付き個数です。

   • n_k はクラス k 内の観測数です。

   • x_ij = L の場合は $$I\left\{x_{ij}=L\right\}=1$$、それ以外の場合は 0 です。

   • $$w_i^{}$$ は観測値 i の重みです。クラス内の重みは、その合計がクラスの事前確率になるように正規化されます。

   • m_j は予測子 j の異なるレベルの数です。

   • m_k はクラス k 内の重み付けされた観測値の数です。

参照

[1] Manning, Christopher D., Prabhakar Raghavan, and Hinrich Schütze. Introduction to Information Retrieval, NY: Cambridge University Press, 2008.

バージョン履歴

R2021a で導入

R2021b: 単純ベイズ インクリメンタル近似関数による条件付き正規予測子変数に対する偏った (最尤) 標準偏差の計算

R2021b 以降、単純ベイズ インクリメンタル近似関数 fit および updateMetricsAndFit は、学習中に条件付き正規予測子変数に対して加重標準偏差の偏った (最尤) 推定値を計算します。つまり、各クラス k に対して、インクリメンタル近似関数は、条件付き正規予測子 x_j の加重偏差の平方和をクラス k の重みの和で正規化します。R2021b より前は、単純ベイズ インクリメンタル近似関数は、fitcnb のような不偏標準偏差を計算していました。現在返される加重標準偏差の推定値は、R2021b より前に計算されていた加重標準偏差と次のファクタだけ異なります。

$$1-\frac{{\displaystyle \sum _{\{i:y_i=k\}}{w}_i{}^2}}{{\left({\displaystyle \sum _{\{i:y_i=k\}}{w}_i}\right)}^2}.$$

このファクタは、標本サイズが大きくなると 1 に近づきます。

参考

関数

• fit | updateMetrics | updateMetricsAndFit | predict | fitcnb | incrementalLearner

トピック

• インクリメンタル学習の概要
• インクリメンタル学習モデルの構成
• 簡潔なワークフローを使用した分類用のインクリメンタル学習の実装
• 柔軟なワークフローを使用した分類用のインクリメンタル学習の実装
• テキスト分類のインクリメント実行
• 単純ベイズと異種混合データでのインクリメンタル学習