fit

インクリメンタル学習用の単純ベイズ分類モデルの学習

R2021a 以降

構文

Mdl = fit(Mdl,X,Y)

Mdl = fit(Mdl,X,Y,'Weights',Weights)

説明

関数 fit は、構成されたインクリメンタル学習用の単純ベイズ分類モデル (incrementalClassificationNaiveBayes オブジェクト) をストリーミングデータに当てはめます。到達したデータを使用して追加的にパフォーマンスメトリクスを追跡するには、代わりに updateMetricsAndFit を使用します。

単純ベイズ分類モデルを一度にデータのバッチ全体に当てはめるか交差検証するには、fitcnb を参照してください。

Mdl = fit(Mdl,X,Y) は、インクリメンタル学習用の単純ベイズ分類モデル Mdl を返します。これは、予測子 X と応答データ Y を使用して学習させたインクリメンタル学習用の入力単純ベイズ分類モデル Mdl を表します。具体的には、fit は与えられたデータに応じて予測子変数の条件付き事後分布を更新します。

例

Mdl = fit(Mdl,X,Y,'Weights',Weights) は、観測値の重み Weights も設定します。

例

すべて折りたたむ

十分な事前情報なしでのモデルのインクリメンタル学習

ライブスクリプトを開く

データに含まれるクラスの想定される最大数のみがわかっている場合にインクリメンタル単純ベイズ学習器を当てはめます。

インクリメンタル単純ベイズモデルを作成します。予測される最大クラス数を 5 と指定します。

Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',5)

Mdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 0
                   Metrics: [1×2 table]
                ClassNames: [1×0 double]
            ScoreTransform: 'none'
         DistributionNames: 'normal'
    DistributionParameters: {}


  Properties, Methods

Mdl は incrementalClassificationNaiveBayes モデルです。そのプロパティはすべて読み取り専用です。Mdl が処理できる一意のクラスは最大 5 つです。既定では、事前クラス分布 Mdl.Prior は経験的であり、ラベルが見つかると事前分布が更新されます。

Mdl は、他の演算の実行に使用する前に、データに当てはめなければなりません。

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

関数 fit を使用してインクリメンタルモデルを学習データに当てはめます。50 個の観測値で構成されるチャンクを一度に当てはめます。各反復で次を行います。

50 個の観測値を処理して、データストリームをシミュレート。
前のインクリメンタルモデルを、入力観測値に当てはめた新しいモデルで上書きします。
1 番目のクラス $μ_{11}$ における 1 番目の予測子の平均と被験者が移動しているかどうか (Y > 2) の事前確率を保存し、インクリメンタル学習中にそれらのパラメーターがどのように進化するかを確認。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
mu11 = zeros(nchunk,1);    
priormoved = zeros(nchunk,1);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = fit(Mdl,X(idx,:),Y(idx));
    mu11(j) = Mdl.DistributionParameters{1,1}(1);
    priormoved(j) = sum(Mdl.Prior(Mdl.ClassNames > 2));
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデルオブジェクトです。

パラメーターがインクリメンタル学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(mu11)
ylabel('\mu_{11}')
xlabel('Iteration')
axis tight
nexttile
plot(priormoved)
ylabel('\pi(Subject Is Moving)')
xlabel(t,'Iteration')
axis tight

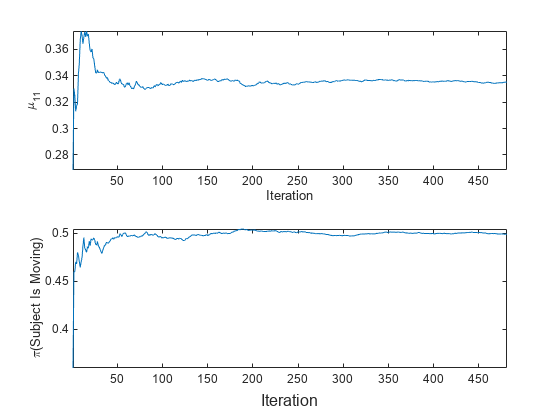
$Figure contains 2 axes objects. Axes object 1 with xlabel Iteration, ylabel \mu_{11} contains an object of type line. Axes object 2 with ylabel \pi(Subject Is Moving) contains an object of type line.$

予測子分布の事後平均は fit で各チャンクが処理されると更新されます。事前クラス分布は経験的であるため、 $π$ (被験者が移動) は fit で各チャンクが処理されると変化します。

すべてのクラス名を指定した状態での当てはめ

ライブスクリプトを開く

データに含まれるすべてのクラス名がわかっている場合にインクリメンタル単純ベイズ学習器を当てはめます。

デバイスに学習させ、被験者で測定された生体データに基づいて、被験者が座る、立つ、歩く、走る、踊るのいずれの状態であるかを予測するとします。各行動にはクラス名 1 ～ 5 をマッピングします。また、この調査では、クラスごとのデバイスの分布は一様になるものとします。

マルチクラス学習用のインクリメンタル単純ベイズモデルを作成します。クラス名および一様な事前クラス分布を指定します。

classnames = 1:5;
Mdl = incrementalClassificationNaiveBayes('ClassNames',classnames,'Prior','uniform')

Mdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 0
                   Metrics: [1×2 table]
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
         DistributionNames: 'normal'
    DistributionParameters: {5×0 cell}


  Properties, Methods

Mdl は incrementalClassificationNaiveBayes モデルオブジェクトです。そのプロパティはすべて読み取り専用です。学習中に観測されるラベルは Mdl.ClassNames のいずれかでなければなりません。

Mdl は、他の演算の実行に使用する前に、データに当てはめなければなりません。

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1); % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

関数 fit を使用して、インクリメンタルモデルを学習データに当てはめます。50 個の観測値のチャンクを一度に処理して、データストリームをシミュレートします。各反復で次を行います。

50 個の観測値を処理します。
前のインクリメンタルモデルを、入力観測値に当てはめた新しいモデルで上書きします。
1 番目のクラス $μ_{11}$ における 1 番目の予測子の平均と被験者が移動しているかどうか (Y > 2) の事前確率を保存し、インクリメンタル学習中にそれらのパラメーターがどのように進化するかを確認。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
mu11 = zeros(nchunk,1);    
priormoved = zeros(nchunk,1);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = fit(Mdl,X(idx,:),Y(idx));
    mu11(j) = Mdl.DistributionParameters{1,1}(1);
    priormoved(j) = sum(Mdl.Prior(Mdl.ClassNames > 2));
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデルオブジェクトです。

パラメーターがインクリメンタル学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(mu11)
ylabel('\mu_{11}')
xlabel('Iteration')
axis tight
nexttile
plot(priormoved)
ylabel('\pi(Subject Is Moving)')
xlabel(t,'Iteration')
axis tight

予測子分布の事後平均は fit で各チャンクが処理されると更新されます。事前クラス分布は一様として指定されているため、 $π$ (被験者が移動) は 0.6 のまま fit で各チャンクが処理されても変化しません。

観測値の重みの指定

ライブスクリプトを開く

fitcnb を使用して単純ベイズ分類モデルに学習させ、それをインクリメンタル学習器に変換し、その性能をストリーミングデータで追跡してからモデルをデータに当てはめます。観測値の重みを指定します。

データの読み込みと前処理

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
rng(1); % For reproducibility
n = numel(actid);
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

静止している被験者 (Y <= 2) のデータが、移動している被験者のデータの倍の品質であると仮定します。静止している被験者の観測値に重み 2 を割り当て、移動している被験者の観測値に重み 1 を割り当てる重み変数を作成します。

W = ones(n,1) + (Y <=2);

単純ベイズ分類モデルの学習

単純ベイズ分類モデルをデータの半分の無作為標本に当てはめます。

idxtt = randsample([true false],n,true);
TTMdl = fitcnb(X(idxtt,:),Y(idxtt),'Weights',W(idxtt))

TTMdl = 
  ClassificationNaiveBayes
              ResponseName: 'Y'
     CategoricalPredictors: []
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
           NumObservations: 12053
         DistributionNames: {1×60 cell}
    DistributionParameters: {5×60 cell}


  Properties, Methods

TTMdl は従来式の学習済み単純ベイズ分類モデルを表す ClassificationNaiveBayes モデルオブジェクトです。

学習済みモデルの変換

従来式の学習済み分類モデルをインクリメンタル学習用の単純ベイズ分類モデルに変換します。

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 1
                   Metrics: [1×2 table]
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
         DistributionNames: {1×60 cell}
    DistributionParameters: {5×60 cell}


  Properties, Methods

IncrementalMdl は incrementalClassificationNaiveBayes モデルです。クラス名が IncrementalMdl.ClassNames で指定されているため、インクリメンタル学習で見つかるラベルは IncrementalMdl.ClassNames のいずれかでなければなりません。

パフォーマンスメトリクスの追跡とモデルの当てはめの個別の実行

関数 updateMetrics および fit を使用して、残りのデータに対してインクリメンタル学習を実行します。各反復で次を行います。

50 個の観測値を一度に処理して、データストリームをシミュレートします。
updateMetrics を呼び出し、観測値の入力チャンクを所与として、モデルの最小コストの累積とウィンドウを更新します。前のインクリメンタルモデルを上書きして、Metrics プロパティ内の損失を更新します。関数がモデルをデータチャンクに当てはめないことに注意してください。チャンクはモデルに対して "新しい" データです。観測値の重みを指定します。
最小コストを保存します。
fit を呼び出して、観測値の入力チャンクにモデルを当てはめます。前のインクリメンタルモデルを上書きして、モデルパラメーターを更新します。観測値の重みを指定します。

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 50;
nchunk = floor(nil/numObsPerChunk);
mc = array2table(zeros(nchunk,2),'VariableNames',["Cumulative" "Window"]);
Xil = X(idxil,:);
Yil = Y(idxil);
Wil = W(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx), ...
        'Weights',Wil(idx));
    mc{j,:} = IncrementalMdl.Metrics{"MinimalCost",:};
    IncrementalMdl = fit(IncrementalMdl,Xil(idx,:),Yil(idx),'Weights',Wil(idx));
end

IncrementalMdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデルオブジェクトです。

あるいは、updateMetricsAndFit を使用して、新しいデータチャンクに対するモデルのパフォーマンスメトリクスを更新し、モデルをデータに当てはめることもできます。

パフォーマンスメトリクスのトレースプロットをプロットします。

h = plot(mc.Variables);
xlim([0 nchunk])
ylabel('Minimal Cost')
legend(h,mc.Properties.VariableNames)
xlabel('Iteration')

Figure contains an axes object. The axes object with xlabel Iteration, ylabel Minimal Cost contains 2 objects of type line. These objects represent Cumulative, Window.

累積の損失は徐々に安定しますが、ウィンドウの損失には学習全体を通じて急な変動があります。

条件付き学習の実行

ライブスクリプトを開く

単純ベイズ分類モデルのパフォーマンスが低下した場合にのみ、そのモデルに対してインクリメンタル学習を行います。

人の行動のデータセットを読み込みます。データをランダムにシャッフルします。

load humanactivity
n = numel(actid);
rng(1) % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データセットの詳細については、コマンドラインで Description を入力してください。

予測される最大クラス数が 5 で、追跡されるパフォーマンスメトリクスに誤分類誤差率を含み、メトリクスウィンドウサイズが 1000 となるように、インクリメンタル学習用の単純ベイズ分類モデルを構成します。構成したモデルを最初の 1000 個の観測値に当てはめます。

Mdl = incrementalClassificationNaiveBayes('MaxNumClasses',5,'MetricsWindowSize',1000, ...
    'Metrics','classiferror');
initobs = 1000;
Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));

Mdl は incrementalClassificationNaiveBayes モデルオブジェクトです。

条件付きの当てはめを行い、インクリメンタル学習を実行します。各反復でこの手順に従います。

100 個の観測値のチャンクを一度に処理することで、データストリームをシミュレートします。
入力データチャンクでモデルのパフォーマンスを更新します。
誤分類誤差率が 0.05 を超える場合にのみ、モデルをデータチャンクに当てはめます。
パフォーマンスと当てはめを追跡するときは、前のインクリメンタルモデルを上書きします。
誤分類誤差率と 2 番目のクラス $μ_{21}$ における 1 番目の予測子の平均を保存し、学習中にそれらがどのように進化するかを確認します。
fit がモデルに学習させるタイミングを追跡します。

% Preallocation
numObsPerChunk = 100;
nchunk = floor((n - initobs)/numObsPerChunk);
mu21 = zeros(nchunk,1);
ce = array2table(nan(nchunk,2),'VariableNames',["Cumulative" "Window"]);
trained = false(nchunk,1);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs);
    iend = min(n,numObsPerChunk*j + initobs);
    idx = ibegin:iend;
    Mdl = updateMetrics(Mdl,X(idx,:),Y(idx));
    ce{j,:} = Mdl.Metrics{"ClassificationError",:};
    if ce{j,2} > 0.05
        Mdl = fit(Mdl,X(idx,:),Y(idx));
        trained(j) = true;
    end    
    mu21(j) = Mdl.DistributionParameters{2,1}(1);
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalClassificationNaiveBayes モデルオブジェクトです。

モデルのパフォーマンスと $μ_{21}$ が学習中にどのように進化するかを確認するには、それらを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(mu21)
hold on
plot(find(trained),mu21(trained),'r.')
xlim([0 nchunk])
ylabel('\mu_{21}')
legend('\mu_{21}','Training occurs','Location','best')
hold off
nexttile
plot(ce.Variables)
xlim([0 nchunk])
ylabel('Misclassification Error Rate')
legend(ce.Properties.VariableNames,'Location','best')
xlabel(t,'Iteration')

$Figure contains 2 axes objects. Axes object 1 with ylabel \mu_{21} contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent \mu_{21}, Training occurs. Axes object 2 with ylabel Misclassification Error Rate contains 2 objects of type line. These objects represent Cumulative, Window.$

$μ_{21}$ のトレースプロットは、前の観測ウィンドウ内における損失が最大で 0.05 である定数値の期間を示します。

入力引数

すべて折りたたむ

`Mdl` — インクリメンタル学習用の単純ベイズ分類モデル
`incrementalClassificationNaiveBayes` モデルオブジェクト

ストリーミングデータに当てはめるインクリメンタル学習用の単純ベイズ分類モデル。incrementalClassificationNaiveBayes モデルオブジェクトとして指定します。Mdl は、直接作成することも、サポートされている従来式の学習済み機械学習モデルを関数 incrementalLearner によって変換して作成することもできます。詳細については、対応するリファレンスページを参照してください。

`X` — 予測子データのチャンク
浮動小数点行列

モデルを当てはめる予測子データのチャンク。n 行 Mdl.NumPredictors 列の浮動小数点行列として指定します。

観測値のラベル Y の長さと X の観測値の数は同じでなければなりません。Y(j) は X 内の観測値 j (行) のラベルです。

メモ

Mdl.NumPredictors = 0 の場合、fit は X から予測子の数を推測し、出力モデルの対応するプロパティを設定します。それ以外の場合、ストリーミングデータ内の予測子変数の数が Mdl.NumPredictors から変化すると、fit がエラーを生成します。

データ型: single | double

`Y` — ラベルのチャンク
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

モデルを当てはめるラベルのチャンク。categorical 配列、文字配列、string 配列、logical ベクトル、浮動小数点ベクトルのいずれか、あるいは文字ベクトルの cell 配列として指定します。

観測値のラベル Y の長さと X の観測値の数は同じでなければなりません。Y(j) は X 内の観測値 j (行) のラベルです。

次の状況のいずれかまたは両方に該当する場合、fit からエラーが発行されます。

Y に新しいラベルが格納された時点で既にクラスの最大数に達していた (incrementalClassificationNaiveBayes の引数 MaxNumClasses および ClassNames を参照)。
入力モデル Mdl の ClassNames プロパティが空以外で、Y と Mdl.ClassNames のデータ型が異なる。

`Weights` — 観測値の重みのチャンク
正の値の浮動小数点ベクトル

観測値の重みのチャンク。正の値の浮動小数点ベクトルとして指定します。fit は、Weights 内の対応する値を使用して X 内の観測値に重みを付けます。Weights のサイズは X 内の観測値の数 n と同じでなければなりません。

既定では Weights は ones(n,1) です。

正規化方式を含む詳細については、観測値の重みを参照してください。

データ型: double | single

メモ

観測値 (予測子またはラベル) または重みが少なくとも 1 つの欠損 (NaN) 値を含む場合、fit はその観測値を無視します。したがって、fit は n 個よりも少ない観測値を使用して更新したモデルを作成します。ここで n は X 内の観測値数です。

出力引数

すべて折りたたむ

`Mdl` — 更新されたインクリメンタル学習用の単純ベイズ分類モデル
`incrementalClassificationNaiveBayes` モデルオブジェクト

更新されたインクリメンタル学習用の単純ベイズ分類モデル。入力モデル Mdl と同じデータ型のインクリメンタル学習モデルオブジェクト incrementalClassificationNaiveBayes として返されます。

分布モデルのパラメーターを更新する以外に、fit は、Y に必要でも未処理のクラスが含まれている場合、次のアクションを実行します。

incrementalClassificationNaiveBayes を使用して入力モデル Mdl を作成する際、名前と値の引数 ClassNames を使用して必要なすべてのクラスを指定しているわけではない場合、fit は以下を実行します。
1. Y 内の新しいラベルを Mdl.ClassNames の末尾に追加します。
2. Mdl.Cost を c 行 c 列の行列に拡張します。ここで c は Mdl.ClassNames のクラスの数です。結果の誤分類コスト行列は釣り合います。
3. Mdl.Prior を更新された経験クラス分布の長さ c のベクトルに拡張します。
入力モデル Mdl を作成する際、または incrementalLearner を使用して従来式の学習済み単純ベイズモデルを変換する際に、必要なすべてのクラスを指定していても、誤分類コスト行列 (Mdl.Cost) を指定していない場合、fit は処理済みクラスの誤分類コストを 1 に、未処理クラスの誤分類コストを NaN に設定します。たとえば、fit が 3 つの可能なクラスのうち最初の 2 つのクラスを処理している場合、Mdl.Cost は [0 1 NaN; 1 0 NaN; 1 1 0] となります。

詳細

すべて折りたたむ

bag-of-tokens モデル

bag-of-tokens モデルでは、予測子 j の値は観測値のトークン j の発生数を表す非負の数値です。この多項モデルのカテゴリ (ビン) の数は、異なるトークンの数 (予測子の数) です。

ヒント

従来式の学習とは異なり、インクリメンタル学習には個別のテスト (ホールドアウト) セットが存在しない場合もあります。そのため、データの各入力チャンクをテストセットとして扱うには、インクリメンタルモデルと各入力チャンクを、同じデータでモデルに学習させる前に updateMetrics に渡します。

アルゴリズム

すべて折りたたむ

正規分布の推定器

予測子変数 j が条件付き正規分布をもつ場合 (DistributionNames プロパティを参照)、クラス固有の加重平均、および加重標準偏差の偏った (最尤) 推定を計算することにより、この分布がデータに当てはめられます。各クラス k に対して以下を実行します。

予測子 j の加重平均は次のようになります。

${\bar{x}}_{j | k} = \frac{\sum_{{i : y_{i} = k}} w_{i} x_{i j}}{\sum_{{i : y_{i} = k}} w_{i}},$
ここで w_i は観測値 i の重みです。クラス内の重みは、その合計がクラスの事前確率になるように正規化されます。
予測子 j の加重標準偏差の不偏推定器は次のようになります。

$s_{j | k} = {[\frac{\sum_{{i : y_{i} = k}} w_{i} {(x_{i j} - {\bar{x}}_{j | k})}^{2}}{\sum_{{i : y_{i} = k}} w_{i}}]}^{1 / 2} .$

多項分布の推定確率

すべての予測子変数が条件付き多項分布を構成する場合 (DistributionNames プロパティを参照)、bag-of-tokens モデルを使用して、この分布が当てはめられます。トークン j がプロパティ DistributionParameters{k,j} のクラス k に出現する確率が保存されます。加法平滑化[1]を使用すると、推定確率は次のようになります。

$P (token j | class k) = \frac{1 + c_{j | k}}{P + c_{k}},$

ここで、以下になります。

$c_{j | k} = n_{k} \frac{\sum_{{i : y_{i} = k}}^{} x_{i j} w_{i}^{}}{\sum_{{i : y_{i} = k}}^{} w_{i}},$ はクラス k におけるトークン j の重み付き発生数です。
n_k はクラス k 内の観測数です。
$w_{i}^{}$ は観測値 i の重みです。クラス内の重みは、その合計がクラスの事前確率になるように正規化されます。
$c_{k} = \sum_{j = 1}^{P} c_{j | k},$ は、クラス k に含まれているすべてのトークンの重み付き発生数の合計です。

多変量多項分布の推定確率

予測子変数 j が条件付き多変量多項分布をもつ場合 (DistributionNames プロパティを参照)、次のような手順になります。

一意のレベルのリストが収集され、並べ替えられたリストは CategoricalLevels に保存され、各レベルはビンと見なされます。予測子とクラスの各組み合わせは、個別の独立した多項確率変数です。
各クラス k に対して、CategoricalLevels{j} に保存されたリストを使用して、カテゴリカルレベルごとのインスタンスがカウントされます。
クラス k の予測子 j が、プロパティ DistributionParameters{k,j} においてレベル L をもつ場合、すべてのレベルの確率は CategoricalLevels{j} に保存されます。加法平滑化[1]を使用すると、推定確率は次のようになります。

$P (predictor j = L | class k) = \frac{1 + m_{j | k} (L)}{m_{j} + m_{k}},$
ここで、以下になります。
- $m_{j | k} (L) = n_{k} \frac{\sum_{{i : y_{i} = k}}^{} I {x_{i j} = L} w_{i}^{}}{\sum_{{i : y_{i} = k}}^{} w_{i}^{}},$ は、クラス k 内の予測子 j が L に等しい観測値の重み付き個数です。
- n_k はクラス k 内の観測数です。
- x_ij = L の場合は $I {x_{i j} = L} = 1$ 、それ以外の場合は 0 です。
- $w_{i}^{}$ は観測値 i の重みです。クラス内の重みは、その合計がクラスの事前確率になるように正規化されます。
- m_j は予測子 j の異なるレベルの数です。
- m_k はクラス k 内の重み付けされた観測値の数です。

観測値の重み

それぞれの条件付き予測子分布について、fit は加重平均と標準偏差を計算します。

事前クラス確率分布が既知の場合 (つまり、事前分布が経験分布でない場合)、fit は、観測値の重みを正規化して、それぞれのクラスの事前クラス確率の合計になるようにします。このアクションは、既定の観測値の重みがそれぞれの事前クラス確率であることを前提としています。

クラスの事前確率分布が経験分布の場合、ソフトウェアは、fit が呼び出されるたびに、指定された観測値の重みを正規化して、合計が 1 になるようにします。

参照

[1] Manning, Christopher D., Prabhakar Raghavan, and Hinrich Schütze. Introduction to Information Retrieval, NY: Cambridge University Press, 2008.

バージョン履歴

R2021a で導入

すべて展開する

R2021b: 単純ベイズインクリメンタル近似関数による条件付き正規予測子変数に対する偏った (最尤) 標準偏差の計算

R2021b 以降、単純ベイズインクリメンタル近似関数 fit および updateMetricsAndFit は、学習中に条件付き正規予測子変数に対して加重標準偏差の偏った (最尤) 推定値を計算します。つまり、各クラス k に対して、インクリメンタル近似関数は、条件付き正規予測子 x_j の加重偏差の平方和をクラス k の重みの和で正規化します。R2021b より前は、単純ベイズインクリメンタル近似関数は、fitcnb のような不偏標準偏差を計算していました。現在返される加重標準偏差の推定値は、R2021b より前に計算されていた加重標準偏差と次のファクタだけ異なります。

$1 - \frac{\sum_{{i : y_{i} = k}} w_{i}^{2}}{{(\sum_{{i : y_{i} = k}} w_{i})}^{2}} .$

このファクタは、標本サイズが大きくなると 1 に近づきます。

fit

構文

説明

例

十分な事前情報なしでのモデルのインクリメンタル学習

すべてのクラス名を指定した状態での当てはめ

観測値の重みの指定

条件付き学習の実行

入力引数

`Mdl` — インクリメンタル学習用の単純ベイズ分類モデル
`incrementalClassificationNaiveBayes` モデルオブジェクト

`X` — 予測子データのチャンク
浮動小数点行列

`Y` — ラベルのチャンク
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

`Weights` — 観測値の重みのチャンク
正の値の浮動小数点ベクトル

出力引数

`Mdl` — 更新されたインクリメンタル学習用の単純ベイズ分類モデル
`incrementalClassificationNaiveBayes` モデルオブジェクト

詳細

bag-of-tokens モデル

ヒント

アルゴリズム

正規分布の推定器

多項分布の推定確率

多変量多項分布の推定確率

観測値の重み

参照

バージョン履歴

R2021b: 単純ベイズインクリメンタル近似関数による条件付き正規予測子変数に対する偏った (最尤) 標準偏差の計算

参考

オブジェクト

関数

トピック

fit

構文

説明

例

十分な事前情報なしでのモデルのインクリメンタル学習

すべてのクラス名を指定した状態での当てはめ

観測値の重みの指定

条件付き学習の実行

入力引数

Mdl — インクリメンタル学習用の単純ベイズ分類モデル incrementalClassificationNaiveBayes モデル オブジェクト

X — 予測子データのチャンク 浮動小数点行列

Y — ラベルのチャンク categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

Weights — 観測値の重みのチャンク 正の値の浮動小数点ベクトル

出力引数

Mdl — 更新されたインクリメンタル学習用の単純ベイズ分類モデル incrementalClassificationNaiveBayes モデル オブジェクト

詳細

bag-of-tokens モデル

ヒント

アルゴリズム

正規分布の推定器

多項分布の推定確率

多変量多項分布の推定確率

観測値の重み

参照

バージョン履歴

R2021b: 単純ベイズ インクリメンタル近似関数による条件付き正規予測子変数に対する偏った (最尤) 標準偏差の計算

参考

オブジェクト

関数

トピック

`Mdl` — インクリメンタル学習用の単純ベイズ分類モデル
`incrementalClassificationNaiveBayes` モデルオブジェクト

`X` — 予測子データのチャンク
浮動小数点行列

`Y` — ラベルのチャンク
categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 浮動小数点ベクトル | 文字ベクトルの cell 配列

`Weights` — 観測値の重みのチャンク
正の値の浮動小数点ベクトル

`Mdl` — 更新されたインクリメンタル学習用の単純ベイズ分類モデル
`incrementalClassificationNaiveBayes` モデルオブジェクト

R2021b: 単純ベイズインクリメンタル近似関数による条件付き正規予測子変数に対する偏った (最尤) 標準偏差の計算