logp

インクリメンタル学習用の単純ベイズ分類モデルの対数条件なし確率密度

R2021a 以降

構文

lp = logp(Mdl,X)

説明

lp = logp(Mdl,X) は、インクリメンタル学習用の単純ベイズ分類モデル Mdl を使用して、予測子データ X の観測値の対数条件なし確率密度 lp を返します。lp を使用して学習データ内の外れ値を特定できます。

例

ストリーミング データの外れ値の検出

fitcnb を使用して単純ベイズ分類モデルに学習させ、それをインクリメンタル学習器に変換してから、そのインクリメンタル モデルを使用してストリーミング データの外れ値を検出します。

データの読み込みと前処理

人の行動のデータ セットを読み込みます。データをランダムにシャッフルします。

load humanactivity
rng(1); % For reproducibility
n = numel(actid);
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

データ セットの詳細については、コマンド ラインで Description を入力してください。

単純ベイズ分類モデルの学習

単純ベイズ分類モデルをデータの約 25% の無作為標本に当てはめます。

idxtt = randsample([true false false false],n,true);
TTMdl = fitcnb(X(idxtt,:),Y(idxtt))

TTMdl = 
  ClassificationNaiveBayes
              ResponseName: 'Y'
     CategoricalPredictors: []
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
           NumObservations: 6167
         DistributionNames: {1×60 cell}
    DistributionParameters: {5×60 cell}


  Properties, Methods

TTMdl は、従来式の学習済みモデルを表す ClassificationNaiveBayes モデル オブジェクトです。

学習済みモデルの変換

従来式の学習済み分類モデルをインクリメンタル学習用の単純ベイズ分類モデルに変換します。

IncrementalMdl = incrementalLearner(TTMdl)

IncrementalMdl = 
  incrementalClassificationNaiveBayes

                    IsWarm: 1
                   Metrics: [1×2 table]
                ClassNames: [1 2 3 4 5]
            ScoreTransform: 'none'
         DistributionNames: {1×60 cell}
    DistributionParameters: {5×60 cell}


  Properties, Methods

IncrementalMdl は incrementalClassificationNaiveBayes オブジェクトです。IncrementalMdl はインクリメンタル学習用の単純ベイズ分類モデルを表し、パラメーター値は TTMdl のパラメーターと同じです。

外れ値の検出

従来式の学習済みモデルと学習データを使用して、外れ値の条件なし密度のしきい値を調べます。外れ値は、密度がしきい値より小さいストリーミング データの観測値です。

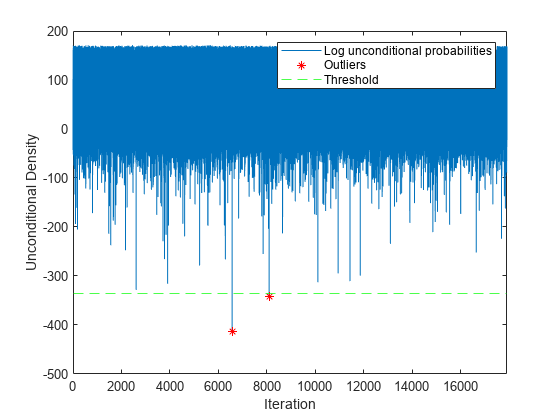
ttlp = logp(TTMdl,X(idxtt,:));
[~,lower] = isoutlier(ttlp)

lower = 
-336.0424

残りのデータでこれらの外れ値を検出します。観測値を一度に 1 個ずつ処理して、データ ストリームをシミュレートします。各反復で logp を呼び出して観測値の対数条件なし確率密度を計算し、それぞれの値を保存します。

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 1;
nchunk = floor(nil/numObsPerChunk);
lp = zeros(nchunk,1);
iso = false(nchunk,1);
Xil = X(idxil,:);
Yil = Y(idxil);

% Incremental processing
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    lp(j) = logp(IncrementalMdl,Xil(idx,:));
    iso(j) = lp(j) < lower;
end

ストリーミング データの対数条件なし確率密度をプロットします。外れ値を特定します。

figure;
h1 = plot(lp);
hold on
x = 1:nchunk;
h2 = plot(x(iso),lp(iso),'r*');
h3 = yline(lower,'g--');
xlim([0 nchunk]);
ylabel('Unconditional Density')
xlabel('Iteration')
legend([h1 h2 h3],["Log unconditional probabilities" "Outliers" "Threshold"])
hold off

入力引数

Mdl — インクリメンタル学習用の単純ベイズ分類モデル

incrementalClassificationNaiveBayes モデル オブジェクト

インクリメンタル学習用の単純ベイズ分類モデル。incrementalClassificationNaiveBayes モデル オブジェクトとして指定します。Mdl は、直接作成することも、サポートされている従来式の学習済み機械学習モデルを関数 incrementalLearner によって変換して作成することもできます。詳細については、対応するリファレンス ページを参照してください。

Mdl は、観測値のバッチで対数条件付き確率密度を計算するように構成しなければなりません。

• Mdl が従来式の学習済みモデルから変換される場合、いかなる修正も行うことなく対数条件付き確率を計算できます。

• それ以外の場合、Mdl.DistributionParameters は、列数が Mdl.NumPredictors > 0 で行数が 1 以上の cell 行列でなければなりません。各行は Mdl.ClassNames の各クラス名に対応します。

X — 予測子データのバッチ

浮動小数点行列

対数条件付き確率密度を計算するための予測子データのバッチ。n 行 Mdl.NumPredictors 列の浮動小数点行列として指定します。

j = 1 ～ n のそれぞれについて、X(j,:) に NaN が少なくとも 1 つ含まれていると、lp(j) は NaN になります。

データ型: single | double

出力引数

lp — 対数条件付き確率密度

浮動小数点ベクトル

対数条件なし確率密度。n 行 1 列の浮動小数点ベクトルとして返されます。lp(j) は、X(j,:) で評価された予測子の対数条件なし確率密度です。

データ型: single | double

詳細

条件なし確率密度

予測子の "条件なし確率密度" はクラスで重視されない密度の分布です。

つまり、条件なし確率密度は次のようになります。

$$P(X_1,\mathrm{..},X_P)={\displaystyle \sum _{k=1}^{K}P}(X_1,\mathrm{..},X_P,Y=k)={\displaystyle \sum _{k=1}^{K}P}(X_1,\mathrm{..},X_P|y=k)\pi (Y=k),$$

ここで、π(Y = k) はクラスの事前確率です。クラス (P(X₁,..,X_P|y = k)) に対するデータの条件付き分布およびクラスの事前確率分布が、学習オプションになります (つまり、分類器を学習させるときにそれらを指定します)。

事前確率

クラスの "事前確率" は、母集団内でそのクラスの観測値が出現すると考えられる相対頻度です。

バージョン履歴

R2021a で導入

参考

オブジェクト

• incrementalClassificationNaiveBayes

関数

• updateMetrics | fit | updateMetricsAndFit | predict

トピック

• インクリメンタル学習の概要
• インクリメンタル学習モデルの構成