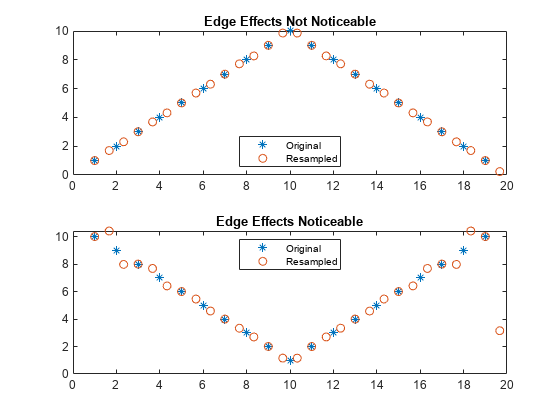
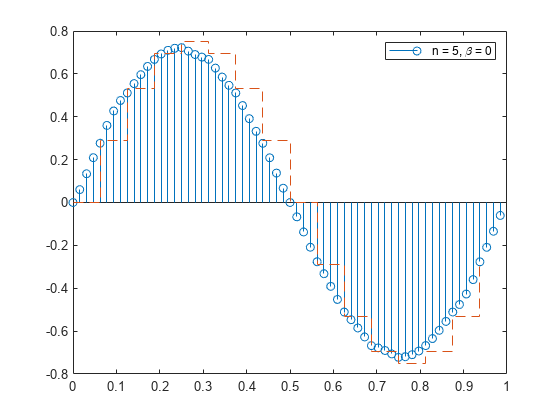
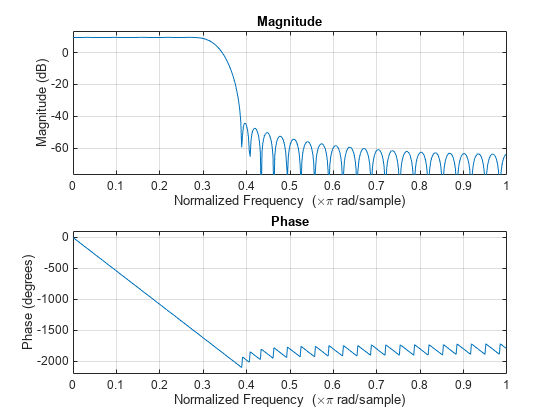
resample
Resample uniform or nonuniform data to new fixed rate
Syntax
Description
y = resample(x,p,q)x, at
p/q times the original sample rate.
resample applies an FIR Antialiasing Lowpass Filter to
x and compensates for the delay introduced by the filter. The
function operates along the first array dimension with size greater than 1.
y = resample(x,tx,fs,p,q)p/q)/fs. The
function then filters the result to upsample it by p and
downsample it by q, resulting in a final sample rate of
fs. For best results, ensure that fs
× q/p is at least twice as large as
the highest frequency component of x.
Examples
Input Arguments
Output Arguments
More About
Tips
Use the
isregularfunction to determine if a timetable is uniformly sampled.
Algorithms
resample performs an FIR design using firls, normalizes the result to account
for the processing gain of the window, and then implements a rate
change using upfirdn.