欠損データの再構成
この例では、内挿、アンチエイリアシング フィルター処理および自己回帰モデリングによる欠損データの再構成方法を説明します。
はじめに
安価なデータ収集ハードウェアの出現に伴い、一定間隔で素早くサンプリングされた信号を利用できる機会が多くなりました。この方法であれば、元の信号に対し精度の高い近似が得られます。しかし、測定しているデータのサンプリングが粗い場合や、データのかなりの部分が欠損している場合は、どうなるでしょうか。把握しているサンプルの間にある点の信号の値はどのような方法で推測すればよいのでしょうか。
線形内挿
線形内挿は、サンプリングされた点の間の値を推測する最も一般的な方法です。MATLAB® でベクトルをプロットする場合、既定では直線で連結された点が表示されます。実際の信号を近似するには、極めて微細な細部まで信号をサンプリングする必要があります。
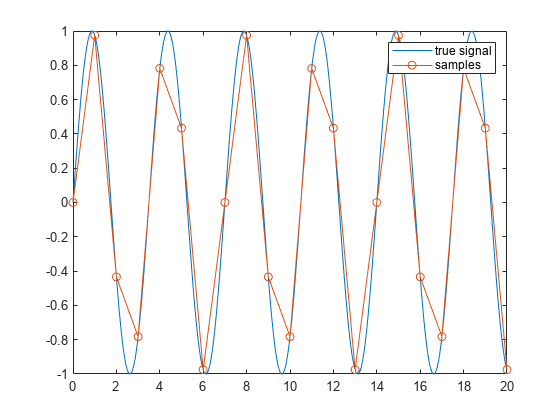
この例では、細かい分解能と粗い分解能の両方で正弦波をサンプリングします。細かくサンプリングされた正弦波をグラフ上にプロットすると、実際の連続正弦波の形状に大変近くなります。したがって、これは "実際の信号" のモデルとして使用することができます。以下のプロットでは、粗くサンプリングされた信号のサンプルが直線でつながれた丸印で示されています。
tTrueSignal = 0:0.01:20; xTrueSignal = sin(2*pi*2*tTrueSignal/7); tSampled = 0:20; xSampled = sin(2*pi*2*tSampled/7); plot(tTrueSignal,xTrueSignal,"-",tSampled,xSampled,"o-") legend("true signal","samples")
plot での内挿の実行と同じ方法で、中間サンプルを簡単に復元できます。これは、関数 interp1 の線形法を使用して実行できます。
tResampled = 0:0.1:20; xLinear = interp1(tSampled,xSampled,tResampled,"linear"); plot(tTrueSignal,xTrueSignal,"-", ... tSampled, xSampled, "o-", ... tResampled,xLinear,".-") legend("true signal","samples","interp1 (linear)")

線形内挿の問題は、結果があまり滑らかにならないことです。この他の内挿法では、より滑らかな近似が得られます。
スプライン内挿
多くの物理量信号は、連続性があり、連続した導関数をもつという点において正弦波と同様です。このような信号は 3 次スプライン内挿を使用して再構成できます。3 次スプライン内挿では、内挿信号の 1 次および 2 次導関数の連続性が各データ点において確保されます。
xSpline = interp1(tSampled,xSampled,tResampled,"spline"); plot(tTrueSignal,xTrueSignal,"-", ... tSampled, xSampled,"o", ... tResampled,xLinear,".-", ... tResampled,xSpline,".-") legend("true signal","samples","interp1 (linear)","interp1 (spline)")
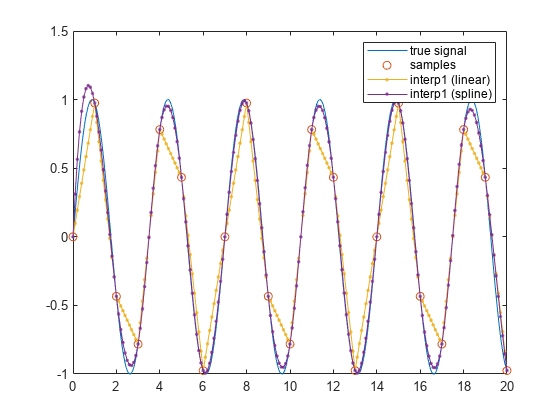
3 次スプラインは、正弦波で構成される信号を内挿する場合に特に有効です。ただし、この他にも、次数が非常に高い連続導関数をもつ物理量信号に対してより高い忠実度を得られる手法があります。
アンチエイリアシング フィルターを使用したリサンプリング
Signal Processing Toolbox の関数 resample には、欠損データを埋める別の手法が用意されています。resample では、歪みを極めて低く抑えて低周波数の正弦波成分を再構成することができます。
xResample = resample(xSampled, 10, 1); tResample = 0.1*((1:numel(xResample))-1); plot(tTrueSignal,xTrueSignal,"-", ... tResampled,xSpline,".", ... tResample, xResample,".") legend("true signal","interp1 (spline)","resample")
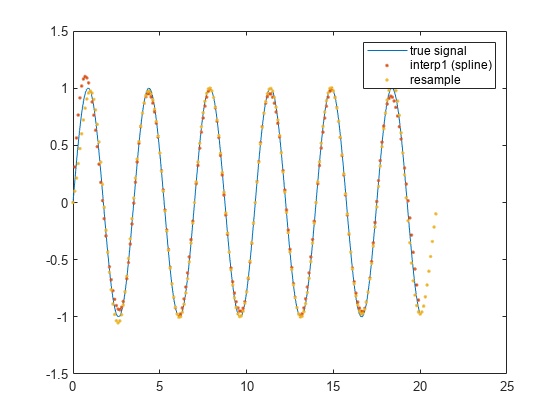
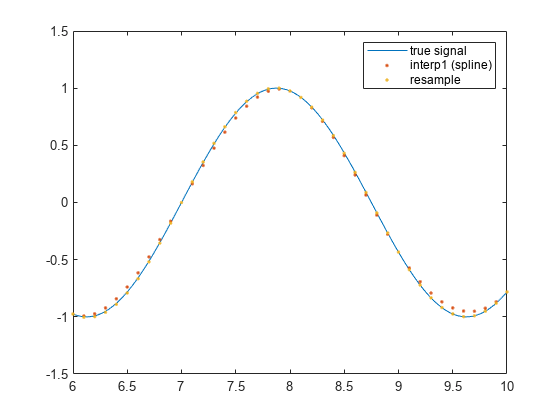
他の手法と同様に、resample でも端点の再構成はやや困難です。一方、再構成した信号の中央部は実際の信号と大変よく合致します。
xlim([6 10])
欠損サンプルを伴うリサンプリング
resample では、不等間隔サンプル信号を調整することができます。この手法は、信号が高レートでサンプリングされている場合に最も効果的です。
次の例では、ゆっくりと移動する正弦波を作成し、サンプルを 1 つ削除してその欠損サンプルの近傍を拡大します。
tTrueSignal = 0:.1:20; xTrueSignal = sin(2*pi*2*tTrueSignal/15); Tx = 0:20; Tmissing = Tx(10); Tx(10) = []; x = sin(2*pi*2*Tx/15); Xmissing = sin(2*pi*2*Tmissing/15); [y, Ty] = resample(x,Tx,10,"spline"); plot(tTrueSignal, xTrueSignal, "-", ... Tmissing,Xmissing,"x ", ... Tx,x,"o ", ... Ty,y,". ") legend("true signal","missing sample", ... "remaining samples","resample with ""spline""") ylim([-1.2 1.2]) xlim([6 14])
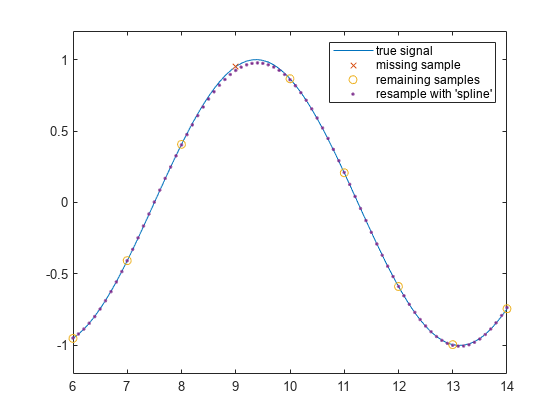
再構成された正弦波は、欠損サンプルの近傍にわずかな誤差があるのみで、実際の信号の形状にかなり近くなっています。
ただし、resample は、信号に大きなギャップがある場合は適切に機能しません。たとえば、中間部分が欠損した減衰正弦波について考えます。
tTrueSignal = (0:199)/199; xTrueSignal = exp(-0.5*tTrueSignal).*sin(2*pi*5*tTrueSignal); tMissing = tTrueSignal; xMissing = xTrueSignal; tMissing(50:140) = []; xMissing(50:140) = []; [y,Ty] = resample(xMissing, tMissing, 200, "spline"); plot(tTrueSignal,xTrueSignal,"-", ... tMissing,xMissing,"o",... Ty,y,".") legend("true signal","samples","resample with ""spline""")
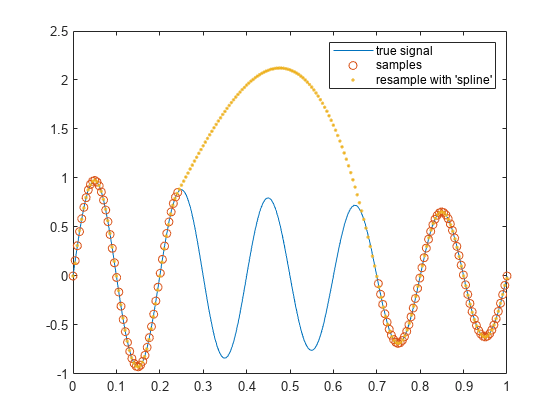
ここで、resample によって再構成された信号は連続的であり、かつ欠損点の近傍で連続導関数をもちます。ただし、欠損部分を適切に再構成することはできません。
大きなギャップの再構成
上記からわかるように、フィルター処理や 3 次内挿だけでは大きなギャップを処理するのに十分ではない場合があります。ただし、振動現象の観察時に発生するような特定の種類の信号をサンプリングした場合には、ギャップの直前または直後のデータに基づいて欠損サンプルの値を推測できることがよくあります。
関数 fillgaps は、自己回帰モデルをギャップ周辺のサンプルに近似し、両方向からギャップに外挿することによって、他の部分では等間隔サンプル信号の欠損サンプル (NaN で指定される) を置き換えることができます。
tTrueSignal = (0:199)/199; xTrueSignal = exp(-.5*tTrueSignal).*sin(2*pi*5*tTrueSignal); gapSignal = xTrueSignal; gapSignal(50:140) = NaN; y = fillgaps(gapSignal); plot(tTrueSignal,xTrueSignal,"-", ... tTrueSignal,gapSignal,"o", ... tTrueSignal,y,".") legend("true signal","samples","reconstructed signal")
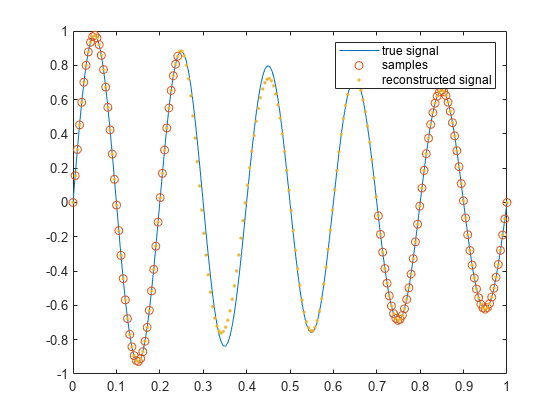
自己回帰信号は多くのサンプルに拡散された情報を含むため、この手法が機能します。信号全体を完全に再構成するのに、任意のセグメント内のわずかなサンプルしか必要としません。
この種類の再構成は、より複雑な信号の欠損サンプルの推定に適合させることができます。ギターの弦を弾く音をサンプリングした音声信号について考えます。弦を弾いた直後の 600 サンプルは除去されています。
[y,fs] = audioread("guitartune.wav"); x = y(1:3500); x(2000:2600) = NaN; y2 = fillgaps(x); plot(1:3500, y(1:3500), "-", ... 1:3500, x, ".", ... 1:3500, y2, "-") legend("original signal","samples","reconstructed signal",... Location="best")
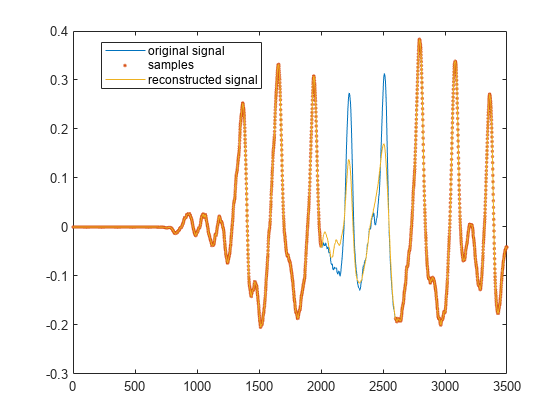
局所的な推定を使用したギャップの再構成
ギャップ近傍の信号を単一の自己回帰過程でモデル化できることがわかっている場合、ギャップ内のデータはかなり容易に埋められます。信号が非定常な自己回帰過程から成る場合は、モデル パラメーターを計算する領域を制限することによって問題を軽減できます。これは、より強い別の共振の直前または直後に発生する 1 つの共振の "リンギング" 期間内にあるギャップを埋める場合に役立ちます。
x = y(350001:370000); x(6000:6950) = NaN; y2 = fillgaps(x); y3 = fillgaps(x,1500); plot(1:20000, y(350001:370000), "-", ... 1:20000, x, ".", ... 1:20000, y2, "-", ... 1:20000, y3, "-") xlim([2200 10200]) legend("original signal","samples", ... "fillgaps (all)","fillgaps (localized)",Location="best")
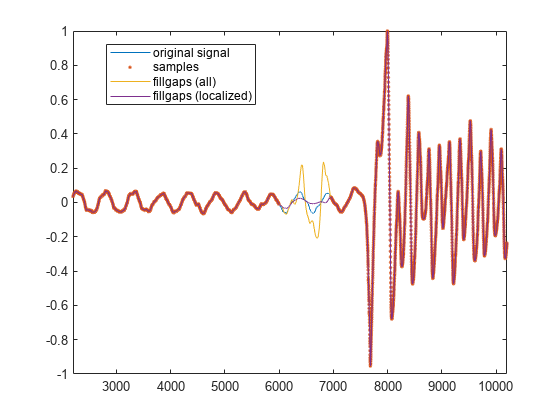
上のプロットでは、大きな共振の直前のセクションが波形から失われています。前と同様に、利用可能なすべてのデータを使用してギャップ領域を外挿するために fillgaps が使用されています。fillgaps の 2 回目の呼び出しでは、ギャップのいずれかの側の 1500 サンプルのみを使用してモデリングを実行しています。これにより、後に続くサンプル 7500 以降のギターの音の影響が軽減されています。
まとめ
内挿、リサンプリングおよび自己回帰モデリングを使用して、隣接するサンプル値から欠損データを再構成する方法をいくつか確認しました。
内挿およびリサンプリングは、緩やかに変化する信号に対して有効です。アンチエイリアシング フィルターを使用したリサンプリングは、低周波数成分で構成された信号の再構成においてより効果的に機能します。振動信号の大きなギャップを再構成するには、ギャップの近傍の自己回帰モデリングが特に有効な場合があります。