このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

intfilt

内挿 FIR フィルターの設計

構文

b = intfilt(l,p,alpha)

b = intfilt(l,n,'Lagrange')

説明

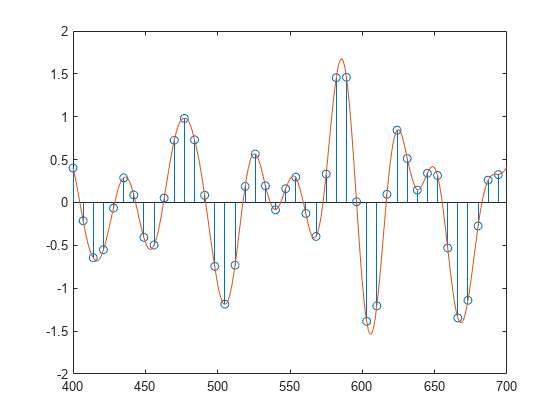
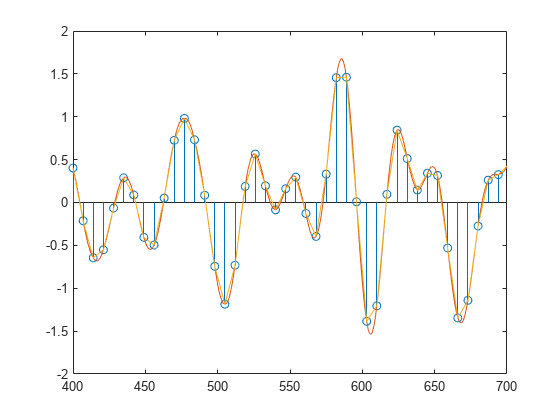
b = intfilt(l,p,alpha) では、ナイキスト周波数を alpha 倍したオリジナルの帯域制約を仮定し、l サンプルごとに l-1 個の連続するゼロが挿入されたシーケンスに使用すると、最近傍の 2*p 個の非ゼロのサンプルを使用して理想的な帯域制限された内挿を行う線形位相 FIR フィルターが設計されます。返されるフィルター b は、interp で使用されるフィルターと同じです。

b = intfilt(l,n,'Lagrange') では、l サンプルごとに l-1 個の連続するゼロが挿入されたシーケンスで、n 次のラグランジュ多項式内挿を行う FIR フィルターが設計されます。

例

デジタル内挿フィルター

帯域制限法を使用して、信号を 7 倍にアップサンプリングするデジタル内挿フィルターを設計します。0.5 の "帯域制限" 係数を指定し、内挿に $$2\times 2$$ サンプルを使用します。

upfac = 7;
alpha = 0.5;
h1 = intfilt(upfac,2,alpha);

フィルターは、元の信号がナイキスト周波数の alpha 倍に帯域制限されたときに、最も適切に機能します。200 個のガウス乱数を生成し、40 次の FIR ローパス フィルターでシーケンスをフィルター処理することによって、帯域制限されたノイズ信号を作成します。再現可能な結果が必要な場合は、乱数発生器をリセットします。

lowp = fir1(40,alpha);

rng('default')
x = filter(lowp,1,randn(200,1));

x の各サンプル ペアの間に 0 を挿入し、信号のサンプル レートを増加させます。

xr = upsample(x,upfac);

関数 filter を使用して内挿信号を出力します。

y = filter(h1,1,xr);

フィルターによって生じた遅延を補正します。元の信号と内挿信号をプロットします。

delay = mean(grpdelay(h1));

y(1:delay) = [];

stem(1:upfac:upfac*length(x),x)
hold on
plot(y)

xlim([400 700])

intfilt は、ラグランジュ多項式内挿も実行します。

• 1 次多項式内挿は単なる線形内挿で、三角フィルターで実現可能。

• 0 次内挿は、移動平均フィルターを使用して実行され、サンプル アンド ホールド表示の出力に類似。

元の信号を内挿して結果を重ね合わせます。

h2 = intfilt(upfac,1,'Lagrange');

y2 = filter(h2,1,xr);
y2(1:floor(mean(grpdelay(h2)))) = [];

plot(y2)
hold off

入力引数

l — サンプル数

正の整数スカラー

サンプル数。正の整数スカラーとして指定します。intfilt では、l サンプルごとに l-1 個の連続するゼロが挿入されたシーケンスを使用して、線形位相 FIR フィルターが設計されます。

p — 非ゼロのサンプル数

正の整数スカラー

非ゼロのサンプル数。正の整数スカラーとして指定します。intfilt では、最近傍の 2*p 個の非ゼロのサンプルを使用して帯域制限された内挿を行う、線形位相 FIR フィルターが設計されます。

alpha — 遷移帯域の逆数測定

スカラー

遷移帯域の逆数測定。スカラーとして指定します。alpha はフィルターの遷移帯域に反比例し、阻止帯域の don't care 領域の帯域幅にも影響します。alpha を指定することで、入力信号がナイキスト区間のどの程度を占めるかを指定できます。これは、内挿に影響せずに遷移帯域幅を増加させることができ、与えられる l と p に対してより良好な阻止帯域の減衰量を得られるため、内挿対象となる信号に有用です。alpha を 1 に設定した場合、信号は全ナイキスト区間を占めると仮定されます。alpha を 1 未満に設定すると、阻止帯域内に don't care 領域を含めることができます。たとえば、入力がナイキスト区間の半分を占める場合は、alpha を 0.5 に設定します。

n — ラグランジュ多項式の次数

正の整数スカラー

ラグランジュ多項式の次数。正の整数スカラーとして指定します。FIR フィルターは、l サンプルごとに、l-1 個の連続するゼロが挿入されたシーケンスで、n 次のラグランジュ多項式内挿を行います。n および l の両方が偶数の場合は、設計されたフィルターは線形位相をもちません。

'Lagrange' — 多項式内挿法

'ラグランジュ'

多項式内挿法。'ラグランジュ' として指定します。

出力引数

b — フィルター係数

ベクトル

フィルター係数。ベクトルとして返されます。b の要素は FIR フィルターの係数です。alpha を指定した場合、ナイキスト周波数を alpha 倍したオリジナルの帯域制約を仮定します。b の長さは 2*l*p-1 となります。

n 次のラグランジュ多項式内挿において、n が偶数の場合は b の長さが (n+1)*l、n が奇数の場合は長さが (n+1)*l-1 となります。

アルゴリズム

帯域制限法では、firls を使用して内挿 FIR が設計されます。多項式法では、等間隔のサンプルにラグランジュの項式内挿公式を使用して、適切なフィルターが作成されます。両タイプのフィルターは、基本的にローパスであり、通過帯域のゲインが l となります。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

すべての入力は定数でなければなりません。式や変数は、その値が変化しない限りは使用できます。

バージョン履歴

R2006a より前に導入

参考

decimate | downsample | interp | resample | upsample