このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
3 軸振動データを使用した産業機械の異常の検出
機械の異常検出は難しいことがよくあります。これは、一般に異常動作よりも定格動作の方が、利用できるデータがはるかに多いためです。2 クラスのモデル学習では、このデータの不均衡により、学習済みモデルの大きいクラスの方に偏る結果となります。
定格状態と異常状態の両方のデータでモデルに学習させる代わりに、モデルがすべての外れ値データを異常として検出する程度の忠実度まで、定格状態のデータのみでモデルに学習させる方法があります。
この例では、そのような方法を用いて、機械学習と深層学習のモデルを使用して産業機械の振動データにおける異常を検出する方法を示します。この例では、機械のデータについて、保守イベントの "前" は異常状態であり、イベントの "後" は定格状態であるとします。このように分けることで、次の図に示すように、学習には定格状態のみのデータを使用し、テストには混在するデータを使用できます。
プロセスの手順は次のとおりです。
1) データ量を減らしたデータ セットを使用して、診断特徴デザイナー アプリを使って生の振動測定値から特徴を抽出、ランク付けして選択します。その後、アプリで生成されたコードを使用して、完全なデータ セット用の選択した特徴を生成します。
2) この特徴データを学習セットと、独立したテスト セットに分割します。その後、学習セットから、ラベルが 'After' のすべての特徴を抽出して、定格状態のデータのみを含む新しい学習セットを作成します。
3) 独立したテスト セットはそのままにします。このテスト セットには、'Before' (異常状態) または 'After' (定格状態) のいずれかのラベルをもつ混在したデータが含まれます。
4) 学習セットを使用して、異常検出用の 3 種類のモデル (1 クラス SVM、孤立森、LSTM ネットワーク) に学習させます。
5) 学習済みの各モデルをテスト セットを使用してテストし、各信号が異常状態であるか定格状態であるかをどの程度うまく識別するかについて、それぞれのモデルを評価して比較します。
データ セットのダウンロードと読み込み
ラベル付きの 3 軸振動測定値を含むデータ セットをダウンロードし、解凍して読み込みます。
url = 'https://ssd.mathworks.com/supportfiles/predmaint/anomalyDetection3axisVibration/v1/vibrationData.zip'; websave('vibrationData.zip',url); unzip('vibrationData.zip'); load("MachineData.mat") head(trainData,3)
ch1 ch2 ch3 label
________________ ________________ ________________ ______
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
{70000×1 double} {70000×1 double} {70000×1 double} Before
各軸のデータは別々の列に保存されています。保守前に収集されたデータはラベルが Before で、異常状態のデータと見なされます。保守後に収集されたデータはラベルが 'After' で、定格状態のデータと見なされます。
データをより良く理解するために、保守前後のデータを可視化します。アンサンブルの 4 番目のメンバーの振動データをプロットします。2 つの状態のプロット データが異なって見える点に注意してください。
ensMember = 4; helperPlotVibrationData(trainData, ensMember)
診断特徴デザイナー アプリによる特徴の抽出
生のデータには相関やノイズが多いため、機械学習モデルの学習に生のデータを使用することは、あまり効率的ではありません。診断特徴デザイナーアプリでは、対話的にデータの調査と前処理を行い、時間ドメインと周波数ドメインの特徴を抽出したうえで特徴をランク付けして、どれが故障やその他の異常システムの診断に最も効果的か判定できます。次に関数をエクスポートして、選択した特徴をデータ セットからプログラムにより抽出できます。コマンド プロンプトで「diagnosticFeatureDesigner」と入力して、診断特徴デザイナーを開きます。診断特徴デザイナーの使用方法のチュートリアルについては、予知保全アルゴリズムの状態インジケーターの設計を参照してください。
[新規セッション] ボタンをクリックし、trainData をソースとして選択してから、label を [状態変数] に設定します。変数 label は、対応するデータについて機械の状態を特定します。
診断特徴デザイナーを使用して特徴について反復し、それらをランク付けできます。アプリによって、生成されたすべての特徴のヒストグラム ビューが作成され、ラベルごとの分布が可視化されます。たとえば、以下のヒストグラムは、ch1 から抽出した各種の特徴の分布を示しています。これらのヒストグラムは、ラベルグループの分離がわかりやすくなるよう、この例で使用するデータ セットよりもはるかに大規模なデータ セットから導出されたものです。使用するデータ セットは比較的小規模であるため、結果は異なります。
各チャネルにつき上位 4 つのランク付けされた特徴を使用します。
ch1:クレスト ファクター、尖度、RMS、標準偏差ch2:平均、RMS、歪度、標準偏差ch3:クレスト ファクター、SINAD、SNR、THD
特徴を生成するための関数を診断特徴デザイナー アプリからエクスポートして、generateFeatures の名前で保存します。この関数はコマンド ラインから、データ セット全体の各チャネルにつき上位 4 つの関連する特徴を抽出します。
trainFeatures = generateFeatures(trainData); head(trainFeatures(:,1:6))
label ch1_stats/Col1_CrestFactor ch1_stats/Col1_Kurtosis ch1_stats/Col1_RMS ch1_stats/Col1_Std ch2_stats/Col1_Mean
______ __________________________ _______________________ __________________ __________________ ___________________
Before 2.2811 1.8087 2.3074 2.3071 -0.032332
Before 2.3276 1.8379 2.2613 2.261 -0.03331
Before 2.3276 1.8626 2.2613 2.2612 -0.012052
Before 2.8781 2.1986 1.8288 1.8285 -0.005049
Before 2.8911 2.06 1.8205 1.8203 -0.0018988
Before 2.8979 2.1204 1.8163 1.8162 -0.0044174
Before 2.9494 1.92 1.7846 1.7844 -0.0067284
Before 2.5106 1.6774 1.7513 1.7511 -0.0089548
学習およびテスト用の完全なデータ セットの準備
ここまでに使用してきたデータ セットは、特徴の抽出と選択の過程を説明するために用いた、はるかに大規模なデータ セットの小さなサブセットに過ぎません。使用可能なすべてのデータでアルゴリズムに学習させると、最良のパフォーマンスがもたらされます。そのために、17,642 の信号からなるより大規模なデータ セットから前もって抽出しておいたものと同じ 12 個の特徴を読み込みます。
load("FeatureEntire.mat")
head(featureAll(:,1:6)) label ch1_stats/Col1_CrestFactor ch1_stats/Col1_Kurtosis ch1_stats/Col1_RMS ch1_stats/Col1_Std ch2_stats/Col1_Mean
______ __________________________ _______________________ __________________ __________________ ___________________
Before 2.3683 1.927 2.2225 2.2225 -0.015149
Before 2.402 1.9206 2.1807 2.1803 -0.018269
Before 2.4157 1.9523 2.1789 2.1788 -0.0063652
Before 2.4595 1.8205 2.14 2.1401 0.0017307
Before 2.2502 1.8609 2.3391 2.339 -0.0081829
Before 2.4211 2.2479 2.1286 2.1285 0.011139
Before 3.3111 4.0304 1.5896 1.5896 -0.0080759
Before 2.2655 2.0656 2.3233 2.3233 -0.0049447
cvpartition を使用して、データを学習セットと、独立したテスト セットに分割します。補助関数 helperExtractLabeledData を使用して、変数 featureTrain 内でラベル 'After' に対応する特徴をすべて検索します。
rng(0) % set for reproducibility idx = cvpartition(featureAll.label, 'holdout', 0.1); featureTrain = featureAll(idx.training, :); featureTest = featureAll(idx.test, :);
それぞれのモデルでは、定格状態であると見なされる、保守後のデータのみで学習を行います。このデータのみを featureTrain から抽出します。
trueAnomaliesTest = featureTest.label;
featureNormal = featureTrain(featureTrain.label=='After', :);1 クラス SVM による異常の検出
サポート ベクター マシンは強力な分類器であり、ここでは定格状態のデータのみで学習するバリアントが使用されています。このモデルは、定格状態のデータから "かけ離れた" 異常の識別に効果的です。ocsvm 関数と定格状態のデータを使用して、1 クラス SVM モデルに学習させます。
rng(0) % For reproducibility mdlOCSVM = ocsvm(featureNormal{:,2:13}, "ContaminationFraction", 0, "StandardizeData", true, "KernelScale", 4);
定格状態と異常状態の両方のデータを含むテスト データを使用して、学習済みの SVM モデルを検証します。
featureTestNoLabels = featureTest(:, 2:end); isanomalyOCSVM = isanomaly(mdlOCSVM, featureTestNoLabels.Variables, "ScoreThreshold", -0.4); predOCSVM = categorical(isanomalyOCSVM, [1, 0], ["Anomaly", "Nominal"]); trueAnomaliesTest = renamecats(trueAnomaliesTest,["After","Before"], ["Nominal","Anomaly"]); figure; confusionchart(trueAnomaliesTest, predOCSVM, Title="Anomaly Detection with One-class SVM", Normalization="row-normalized");
混同行列から、1 クラス SVM がうまく機能していることがわかります。真陽性識別率が高く、誤分類率が非常に小さくなっています。
孤立森による異常の検出
孤立森の決定木では、各観測を 1 枚の葉に分離します。サンプルがその葉に至るためにいくつの判定を通過するかは、それを他から分離するのがどの程度困難であったかの尺度です。特定サンプルの木の平均深度は異常のスコアとして使用され、iforest によって返されます。
定格状態のデータのみで孤立森モデルに学習させます。
[mdlIF,~,scoreTrainIF] = iforest(featureNormal{:,2:13},'ContaminationFraction',0, 'NumLearners', 200, "NumObservationsPerLearner", 512);テスト データを使用して、学習済みの孤立森モデルを検証します。混同チャートを使用して、このモデルのパフォーマンスを可視化します。
[isanomalyIF,scoreTestIF] = isanomaly(mdlIF,featureTestNoLabels.Variables, 'ScoreThreshold', 0.535); predIF = categorical(isanomalyIF, [1, 0], ["Anomaly", "Nominal"]); figure; confusionchart(trueAnomaliesTest,predIF,Title="Anomaly Detection with Isolation Forest",Normalization="row-normalized");
このデータでは、孤立森は 1 クラス SVM ほどうまく機能しません。孤立森モデルのパフォーマンスは、追加データとハイパーパラメーター調整のアクティビティによってさらに改善できます。
双方向 LSTM ネットワークによる異常の検出
双方向 LSTM (BiLSTM) ネットワークはニューラル ネットワークの一種で、過去のコンテキストと将来のコンテキストの両方を考慮してシーケンス データを処理するように設計されています。BiLSTM ネットワークは、時系列データにおける逐次的な依存関係を把握するのに優れています。このコンテキストでは、定格状態のデータのシーケンスのみを使用して BiLSTM ネットワークに学習させることで、想定されるパターンに従わない信号の異常や逸脱を効果的に識別できます。
まず、保守後のデータから特徴を抽出します。
featuresAfter = helperExtractLabeledData(featureTrain, ... "After");
BiLSTM ネットワークを構成し、学習オプションを設定します。
featureDimension = 1; % Define biLSTM network layers layers = [ sequenceInputLayer(featureDimension) bilstmLayer(16) reluLayer bilstmLayer(32) reluLayer bilstmLayer(16) reluLayer fullyConnectedLayer(featureDimension)]; % Set Training Options options = trainingOptions('adam', ... 'Plots', 'training-progress', ... 'Metrics', 'rmse', ... 'MiniBatchSize', 500,... 'MaxEpochs',200, ... 'Verbose',false);
学習オプション パラメーター MaxEpochs は 200 に設定されます。検証の精度を高めるには、このパラメーターをより大きい数に設定することができます。ただし、ネットワークが過適合になる可能性があります。
trainnet を使用してモデルを学習させ、損失関数として平均二乗誤差 (mse) を指定します。
net = trainnet(featuresAfter, featuresAfter, layers, "mse", options);
検証データでのモデル動作と誤差の可視化
Anomalous 状態と Nominal 状態からそれぞれ 1 つのサンプルを抽出し、可視化します。以下のプロットでは、12 個の特徴 (X 軸上に表示) のそれぞれについて、BiLSTM モデルの再構成誤差を示しています。このプロットでは、再構成された特徴値を "Reconstructed" 信号と示してあります。このサンプルでは、特徴 10、11、12 が異常入力に対してうまく再構成されず、したがって、誤差が大きくなります。再構成誤差を使用して異常を特定できます。
testNormal = featureTest(1200, 2:end).Variables'; testAnomaly = featureTest(201, 2:end).Variables'; % Predict decoded signal for both reconstructedNormal = predict(net,testNormal); reconstructedAnomaly = predict(net,testAnomaly); % Visualize helperVisualizeModelBehavior(testNormal, testAnomaly, reconstructedNormal, reconstructedAnomaly)
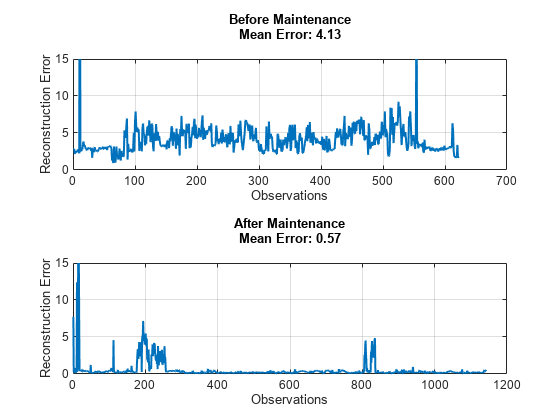
すべての定格状態のデータと異常状態のデータの特徴を抽出します。学習済み BiLSTM モデルを使用して、保守前と保守後の両方のデータについて、選択した 12 個の特徴を予測します。以下のプロットは、12 個の特徴の平方根平均二乗再構成誤差を示したものです。図には、異常状態のデータの再構成誤差が定格状態のデータよりはるかに高いことが示されています。ネットワークは定格状態のデータで学習したため、類似する信号をよりうまく再構成するという結果は予想どおりです。
% Extract data Before maintenance XTestBefore = helperExtractLabeledData(featureTest, "Before"); % Predict output before maintenance and calculate error yHatBefore = minibatchpredict(net, XTestBefore, 'UniformOutput', false); errorBefore = helperCalculateError(XTestBefore, yHatBefore); % Extract data after maintenance XTestAfter = helperExtractLabeledData(featureTest, "After"); % Predict output after maintenance and calculate error yHatAfter = minibatchpredict(net, XTestAfter, 'UniformOutput', false); errorAfter = helperCalculateError(XTestAfter, yHatAfter); helperVisualizeError(errorBefore, errorAfter);
異常の特定
検証データ全体について、再構成誤差を計算します。
XTestAll = helperExtractLabeledData(featureTest, "All"); yHatAll = minibatchpredict(net, XTestAll, 'UniformOutput', false); errorAll = helperCalculateError(XTestAll, yHatAll);
再構成誤差がすべての観測の平均の 0.5 倍となっている点を異常と定義します。このしきい値は前回の実験を通して決定されたものであり、必要に応じて変更することができます。
thresh = 0.55; anomalies = errorAll > thresh*mean(errorAll); helperVisualizeAnomalies(anomalies, errorAll, featureTest);
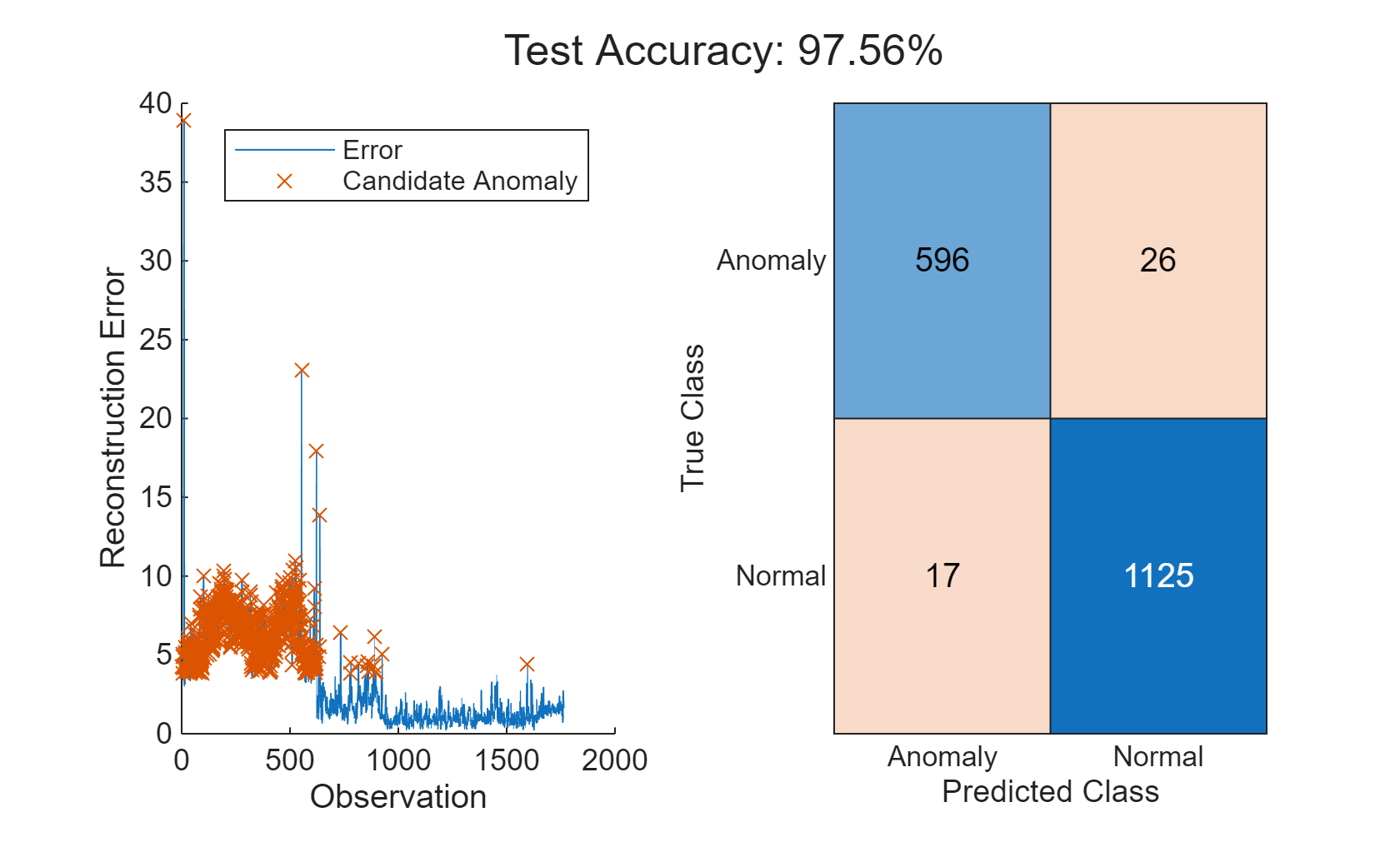
この例では、3 種類のモデルを使用して異常を検出しています。3 つのいずれのモデルでも、高い精度と低い誤分類率で異常を検出できます。モデルの相対的なパフォーマンスは、別の特徴セットを選択した場合や、各モデルに別のハイパーパラメーターを使用した場合に変化する可能性があります。診断特徴デザイナー MATLAB アプリを使用して、さらに特徴選択を試してみましょう。
サポート関数
function E = helperCalculateError(X, Y) % HELPERCALCULATEERROR calculates the rms error value between the % inputs X, Y E = zeros(length(X),1); for i = 1:length(X) E(i,:) = sqrt(sum((Y{i} - X{i}).^2)); end end function helperVisualizeError(errorBefore, errorAfter) % HELPERVISUALIZEERROR creates a plot to visualize the errors on detecting % before and after conditions figure("Color", "W") tiledlayout("flow") nexttile plot(1:length(errorBefore), errorBefore, 'LineWidth',1.5), grid on title(["Before Maintenance", ... sprintf("Mean Error: %.2f\n", mean(errorBefore))]) xlabel("Observations") ylabel("Reconstruction Error") ylim([0 15]) nexttile plot(1:length(errorAfter), errorAfter, 'LineWidth',1.5), grid on, title(["After Maintenance", ... sprintf("Mean Error: %.2f\n", mean(errorAfter))]) xlabel("Observations") ylabel("Reconstruction Error") ylim([0 15]) end function helperVisualizeAnomalies(anomalies, errorAll, featureTest) % HELPERVISUALIZEANOMALIES creates a plot of the detected anomalies anomalyIdx = find(anomalies); anomalyErr = errorAll(anomalies); predAE = categorical(anomalies, [1, 0], ["Anomaly", "Nominal"]); trueAE = renamecats(featureTest.label,["Before","After"],["Anomaly","Nominal"]); acc = numel(find(trueAE == predAE))/numel(predAE)*100; figure; t = tiledlayout("flow"); title(t, "Test Accuracy: " + round(mean(acc),2) + "%"); nexttile hold on plot(errorAll) plot(anomalyIdx, anomalyErr, 'x') hold off ylabel("Reconstruction Error") xlabel("Observation") legend("Error", "Candidate Anomaly") nexttile confusionchart(trueAE,predAE) end function helperVisualizeModelBehavior(normalData, abnormalData, reconstructedNorm, reconstructedAbNorm) %HELPERVISUALIZEMODELBEHAVIOR Visualize model behavior on sample validation data figure("Color", "W") tiledlayout("flow") nexttile() hold on colororder('default') yyaxis left plot(normalData') plot(reconstructedNorm',":","LineWidth",1.5) hold off title("Nominal Input") grid on ylabel("Feature Value") yyaxis right stem(abs(normalData' - reconstructedNorm')) ylim([0 2]) ylabel("Error") legend(["Input", "Reconstructed","Error"],"Location","southwest") nexttile() hold on yyaxis left plot(abnormalData) plot(reconstructedAbNorm',":","LineWidth",1.5) hold off title("Abnormal Input") grid on ylabel("Feature Value") yyaxis right stem(abs(abnormalData' - reconstructedAbNorm')) ylim([0 2]) ylabel("Error") legend(["Input", "Reconstructed","Error"],"Location","southwest") end function X = helperExtractLabeledData(featureTable, label) %HELPEREXTRACTLABELEDDATA Extract data from before or after operating %conditions and re-format to support input to biLSTM network % Select data with label After if label == "All" Xtemp = featureTable(:, 2:end).Variables; else tF = featureTable.label == label; Xtemp = featureTable(tF, 2:end).Variables; end % Arrange data into cells X = cell(length(Xtemp),1); for i = 1:length(Xtemp) X{i,:} = Xtemp(i,:)'; end end
参考
cvpartition | OneClassSVM | fitcsvm | iforest | 診断特徴デザイナー
トピック
- 予知保全アルゴリズムの状態インジケーターの設計
- 教師なし異常検出
- 孤立森による異常検出
- 長短期記憶ニューラル ネットワーク (Deep Learning Toolbox)
