checkGradients

有限差分近似に対する 1 階微分関数の確認

R2023b 以降

ページ内をすべて折りたたむ

構文

valid = checkGradients(fun,x0)

valid = checkGradients(fun,x0,options)

valid = checkGradients(___,Name=Value)

[valid,err] = checkGradients(___)

説明

valid = checkGradients(fun,x0) は、x0 に近い点における fun で指定された 1 階微分関数の値と有限差分近似を比較します。既定では、この関数が目的関数であると想定して比較が行われます。制約関数を確認するには、名前と値の引数 IsConstraint を true に設定します。

例

valid = checkGradients(fun,x0,options) は、有限差分オプションを変更して比較を変更します。

例

valid = checkGradients(___,Name=Value) は、前述の構文の任意の入力引数の組み合わせに加え、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、比較の許容誤差を設定したり、比較の対象が非線形制約関数であることを指定したりできます。

例

[valid,err] = checkGradients(___) は、指定された微分と有限差分近似の相対差を含む構造体 err も返します。

例

すべて折りたたむ

目的関数の勾配の確認

ライブスクリプトを開く

rosen 関数 (この例の終わりに掲載) が、2 次元変数 x の Rosenbrock 目的関数とその勾配を計算します。

rosen で計算された勾配が点 [2,4] 付近の有限差分近似と一致することを確認します。

x0 = [2,4];
valid = checkGradients(@rosen,x0)

valid = logical
   1

function [f,g] = rosen(x)
f = 100*(x(1) - x(2)^2)^2 + (1 - x(2))^2;
if nargout > 1
    g(1) = 200*(x(1) - x(2)^2);
    g(2) = -400*x(2)*(x(1) - x(2)^2) - 2*(1 - x(2));
end
end

最小二乗目的関数の勾配の確認

ライブスクリプトを開く

vecrosen 関数 (この例の終わりに掲載) が、最小二乗形式の Rosenbrock 目的関数とそのヤコビアン (勾配) を計算します。

vecrosen で計算された勾配が点 [2,4] 付近の有限差分近似と一致することを確認します。

x0 = [2,4];
valid = checkGradients(@vecrosen,x0)

valid = logical
   1

function [f,g] = vecrosen(x)
f = [10*(x(1) - x(2)^2),1-x(1)];
if nargout > 1
    g = zeros(2); % Allocate g
    g(1,1) = 10; % df(1)/dx(1)
    g(1,2) = -20*x(2); % df(1)/dx(2)
    g(2,1) = -1; % df(2)/dx(1)
    g(2,2) = 0; % df(2)/dx(2)
end
end

有限差分オプションの変更

ライブスクリプトを開く

rosen 関数 (この例の終わりに掲載) が、2 次元変数 x の Rosenbrock 目的関数とその勾配を計算します。

一部の初期点では、既定の前進有限差分法を使用すると、checkGradients が誤って rosen 関数の勾配が正しくないと示します。結果の詳細を表示するには、Display オプションを "on" に設定します。

x0 = [0,0];
valid = checkGradients(@rosen,x0,Display="on")

____________________________________________________________

Objective function derivatives:
Maximum relative difference between supplied 
and finite-difference derivatives = 1.48826e-06.
  Supplied derivative element (1,1): -0.126021
  Finite-difference derivative element (1,1): -0.126023

checkGradients failed.

Supplied derivative and finite-difference approximation are
not within 'Tolerance' (1e-06).
____________________________________________________________

valid = logical
   0

checkGradients は、小数第 6 位に 1 をわずかに超える差があるという不一致を報告します。中心有限差分法を使用してもう一度確認します。

opts = optimoptions("fmincon",FiniteDifferenceType="central");
valid = checkGradients(@rosen,x0,opts,Display="on")

____________________________________________________________

Objective function derivatives:
Maximum relative difference between supplied 
and finite-difference derivatives = 1.29339e-11.

checkGradients successfully passed.
____________________________________________________________

valid = logical
   1

中心有限差分法の方が一般的に正確性が増します。checkGradients は、勾配と中心有限差分近似がおおよそ小数第 11 位まで一致することを報告します。

function [f,g] = rosen(x)
f = 100*(x(1) - x(2)^2)^2 + (1 - x(2))^2;
if nargout > 1
    g(1) = 200*(x(1) - x(2)^2);
    g(2) = -400*x(2)*(x(1) - x(2)^2) - 2*(1 - x(2));
end
end

非線形制約の勾配の確認

ライブスクリプトを開く

tiltellipse 関数 (この例の終わりに掲載) が、2 次元変数 x が傾いた楕円の内部に限定されるという制約を課します。

$\frac{x y}{2} + (x + 2)^{2} + \frac{(y - 2)^{2}}{2} \leq 2$ .

楕円を可視化します。

f = @(x,y) x.*y/2+(x+2).^2+(y-2).^2/2-2;
fcontour(f,LevelList=0)
axis([-6 0 -1 7])

Figure contains an axes object. The axes object contains an object of type functioncontour.

この非線形不等式制約関数の勾配を確認します。

x0 = [-2,6];
valid = checkGradients(@tiltellipse,x0,IsConstraint=true)

valid = 1×2 logical array

   1   1

function [c,ceq,gc,gceq] = tiltellipse(x)
c = x(1)*x(2)/2 + (x(1) + 2)^2 + (x(2)- 2)^2/2 - 2;
ceq = [];

if nargout > 2
   gc = [x(2)/2 + 2*(x(1) + 2);
       x(1)/2 + x(2) - 2];
   gceq = [];
end
end

勾配と有限差分近似の差の確認

ライブスクリプトを開く

fungrad 関数 (この例の終わりに掲載) が、最小二乗目的関数の一部の要素の勾配を正しく計算し、その他の要素の勾配は正しく計算しません。

checkGradients の 2 番目の出力を調べて、どの要素が点 [2,4] であまり一致していないかを確認します。結果の詳細を表示するには、Display オプションを "on" に設定します。

x0 = [2,4];
[valid,err] = checkGradients(@fungrad,x0,Display="on")

____________________________________________________________

Objective function derivatives:
Maximum relative difference between supplied 
and finite-difference derivatives = 0.749797.
  Supplied derivative element (3,2): 19.9838
  Finite-difference derivative element (3,2): 5

checkGradients failed.

Supplied derivative and finite-difference approximation are
not within 'Tolerance' (1e-06).
____________________________________________________________

valid = logical
   0

err = struct with fields:
    Objective: [3×2 double]

出力から、要素 [3,2] が正しくないことがわかります。しかし、問題はそれだけでしょうか。err.Objective を調べて、0 とかけ離れているエントリを探します。

err.Objective

ans = 3×2

    0.0000    0.0000
    0.0000         0
    0.5000    0.7498

微分の [3,1] と [3,2] の要素がどちらも正しくありません。fungrad2 関数 (この例の終わりに掲載) が、誤差を修正します。

[valid,err] = checkGradients(@fungrad2,x0,Display="on")

____________________________________________________________

Objective function derivatives:
Maximum relative difference between supplied 
and finite-difference derivatives = 2.2338e-08.

checkGradients successfully passed.
____________________________________________________________

valid = logical
   1

err = struct with fields:
    Objective: [3×2 double]

err.Objective

ans = 3×2
10^-7 ×

    0.2234    0.0509
    0.0003         0
    0.0981    0.0042

勾配と有限差分近似の差がすべて 1e-7 未満の大きさになっています。

次のコードは、fungrad 補助関数を作成します。

function [f,g] = fungrad(x)
f = [10*(x(1) - x(2)^2),1 - x(1),5*(x(2) - x(1)^2)];

if nargout > 1
    g = zeros(3,2);
    g(1,1) = 10;
    g(1,2) = -20*x(2);
    g(2,1) = -1;
    g(3,1) = -20*x(1);
    g(3,2) = 5*x(2);
end
end

次のコードは、fungrad2 補助関数を作成します。

function [f,g] = fungrad2(x)
f = [10*(x(1) - x(2)^2),1 - x(1),5*(x(2) - x(1)^2)];

if nargout > 1
    g = zeros(3,2);
    g(1,1) = 10;
    g(1,2) = -20*x(2);
    g(2,1) = -1;
    g(3,1) = -10*x(1);
    g(3,2) = 5;
end
end

`lsqcurvefit` の勾配の確認

ライブスクリプトを開く

勾配評価関数を指定すると、lsqcurvefit などの非線形最小二乗ソルバーは、実行の速度および信頼性が向上する場合があります。ただし、勾配を確認するための lsqcurvefit ソルバーの構文は、他のソルバーと比べてわずかに異なります。

近似問題と checkGradient の構文

lsqcurvefit の勾配を確認するには、初期点 x0 を配列として渡すのではなく、cell 配列 {x0,xdata} を渡します。たとえば、応答関数 $y = a + b \exp (- c x)$ について、ノイズを追加したモデルからデータ ydata を作成します。応答関数は fitfun です。

function [F,J] = fitfun(x,xdata)
F = x(1) + x(2)*exp(-x(3)*xdata);
if nargout > 1
    J = [ones(size(xdata)) exp(-x(3)*xdata) -xdata.*x(2).*exp(-x(3)*xdata)];
end
end

xdata を 0 ～ 10 のランダムな点として作成し、ydata を応答と追加ノイズとして作成します。

a = 2;
b = 5;
c = 1/15;
N = 100;
rng default
xdata = 10*rand(N,1);
fun = @fitfun;
ydata = fun([a,b,c],xdata) + randn(N,1)/10;

応答関数の勾配が点 [a,b,c] で正しいことを確認します。

[valid,err] = checkGradients(@fitfun,{[a b c] xdata})

valid = logical
   1

err = struct with fields:
    Objective: [100×3 double]

指定した目的関数の勾配を問題なく使用できます。すべてのパラメーターの下限を 0 に設定し、上限は指定しません。

options = optimoptions("lsqcurvefit",SpecifyObjectiveGradient=true);
lb = zeros(1,3);
ub = [];
[sol,res,~,eflag,output] = lsqcurvefit(fun,[1 2 1],xdata,ydata,lb,ub,options)

Local minimum possible.

lsqcurvefit stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

<stopping criteria details>

sol = 1×3

    2.5872    4.4376    0.0802

res = 
1.0096

eflag = 
3

output = struct with fields:
      firstorderopt: 4.4156e-06
         iterations: 25
          funcCount: 26
       cgiterations: 0
          algorithm: 'trust-region-reflective'
           stepsize: 1.8029e-04
            message: 'Local minimum possible.↵↵lsqcurvefit stopped because the final change in the sum of squares relative to ↵its initial value is less than the value of the function tolerance.↵↵<stopping criteria details>↵↵Optimization stopped because the relative sum of squares (r) is changing↵by less than options.FunctionTolerance = 1.000000e-06.'
       bestfeasible: []
    constrviolation: []

lsqcurvefit の非線形制約関数

非線形制約関数で必要となる構文は、lsqcurvefit 目的関数の構文とは異なります。勾配のある非線形制約関数の形式は次のとおりです。

function [c,ceq,gc,gceq] = ccon(x)
c = ...
ceq = ...
if nargout > 2
    gc = ...
    gceq = ...
end
end

勾配の式のサイズは N 行 Nc 列にする必要があります。ここで、N は問題変数の数、Nc は制約関数の数です。たとえば、次の ccon 関数は非線形不等式制約を 1 つだけもちます。そのため、この関数は、3 つの変数をもつ次の問題についてサイズが 3 行 1 列の勾配を返します。

function [c,ceq,gc,gceq] = ccon(x)
ceq = [];
c = x(1)^2 + x(2)^2 + 1/x(3)^2 - 50;
if nargout > 2
    gceq = [];
    gc = zeros(3,1); % Gradient is a column vector
    gc(1) = 2*x(1);
    gc(2) = 2*x(2);
    gc(3) = -2/x(3)^3;
end
end

ccon 関数が点 [a,b,c] で正しい勾配を返すかどうかを確認します。

[valid,err] = checkGradients(@ccon,[a b c],IsConstraint=true)

valid = 1×2 logical array

   1   1

err = struct with fields:
    Inequality: [3×1 double]
      Equality: []

制約の勾配を使用するには、勾配関数を使用するオプションを設定し、非線形制約を使用して問題を再度解きます。

options.SpecifyConstraintGradient = true;
[sol2,res2,~,eflag2,output2] = lsqcurvefit(@fitfun,[1 2 1],xdata,ydata,lb,ub,[],[],[],[],@ccon,options)

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

sol2 = 1×3

    4.4436    2.8548    0.2127

res2 = 
2.2623

eflag2 = 
1

output2 = struct with fields:
         iterations: 15
          funcCount: 22
    constrviolation: 0
           stepsize: 1.7914e-06
          algorithm: 'interior-point'
      firstorderopt: 3.3350e-06
       cgiterations: 0
            message: 'Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 1.621619e-07,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 0.000000e+00, is less than options.ConstraintTolerance = 1.000000e-06.'
       bestfeasible: [1×1 struct]

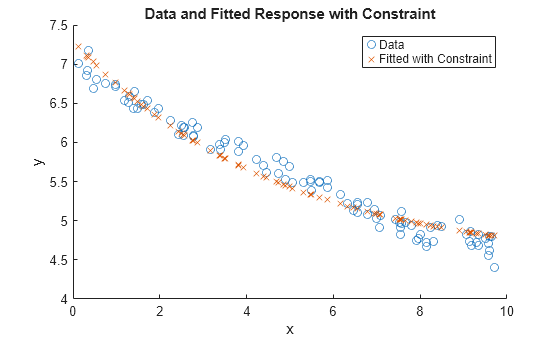
残差 res2 は、非線形制約がない残差 res の 2 倍を上回っています。この結果から、非線形制約によって解と制約なしの最小値に差が生じていることがわかります。

非線形制約を課す場合と課さない場合の解をプロットします。

scatter(xdata,ydata)
hold on
scatter(xdata,fitfun(sol,xdata),"x")
hold off
xlabel("x")
ylabel("y")
legend("Data","Fitted")
title("Data and Fitted Response, No Constraint")

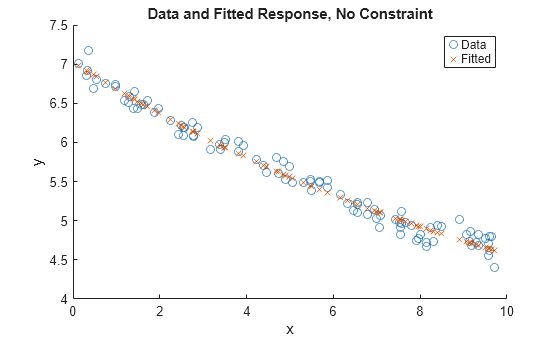
Figure contains an axes object. The axes object with title Data and Fitted Response, No Constraint, xlabel x, ylabel y contains 2 objects of type scatter. These objects represent Data, Fitted.

figure
scatter(xdata,ydata)
hold on
scatter(xdata,fitfun(sol2,xdata),"x")
hold off
xlabel("x")
ylabel("y")
legend("Data","Fitted with Constraint")
title("Data and Fitted Response with Constraint")

Figure contains an axes object. The axes object with title Data and Fitted Response with Constraint, xlabel x, ylabel y contains 2 objects of type scatter. These objects represent Data, Fitted with Constraint.

入力引数

すべて折りたたむ

`fun` — 確認する関数
関数ハンドル

確認する関数。関数ハンドルとして指定します。

fun が目的関数を表す場合、fun には次のシグネチャが必要です。
```
[fval,grad] = fun(x)
```
checkGradients は、grad(x) の値と x0 に近い点 x の有限差分近似を比較します。比較は次のとおりです。
$| \frac{grad_fd - grad}{max (1, | grad |)} |,$
ここで、grad は勾配関数の値を表し、grad_fd は有限差分近似の値を表します。checkGradients はこの除算を要素単位で実行します。
fun が最小二乗目的を表す場合、fun はベクトルであり、grad(x) は fun のヤコビアンを表す行列です。
fun が m 個の成分をもつ配列を返し、x が n 個の要素をもつ場合 (ここで、n は x0 の要素数)、ヤコビアン J は m 行 n 列の行列になります。ここで、J(i,j) は F(i) の x(j) における偏導関数です。(ヤコビアン J は、F の勾配の転置であることに注意してください。)
fun が非線形制約を表す場合、fun には次のシグネチャが必要です。
```
[c,ceq,gc,gceq] = fun(x)
```
- c は、非線形不等式制約を表します。ソルバーは c <= 0 を満たそうとします。c の出力は任意の長さのベクトルになります。
- ceq は、非線形等式制約を表します。ソルバーは ceq = 0 を満たそうとします。ceq の出力は任意の長さのベクトルになります。
- gc は、非線形不等式制約の勾配を表します。勾配のサイズは N 行 Nc 列にする必要があります。ここで、N は問題変数の数、Nc は c の要素数です。
- gceq は、非線形等式制約の勾配を表します。勾配のサイズは N 行 Nceq 列にする必要があります。ここで、N は問題変数の数、Nceq は ceq の要素数です。

データ型: function_handle

`x0` — 勾配を確認する位置
double 配列 | 1 行 2 列の cell 配列

勾配を確認する位置。lsqcurvefit を除くすべてのソルバーについては double 配列として指定します。lsqcurvefit の場合、x0 は 1 行 2 列の cell 配列 {x0array,xdata} です。

checkGradients は、指定された x0 に近い点における勾配を確認します。この関数は、絶対値が 1e-3 以下の小さなランダム方向を x0 に追加します。この摂動は、相殺が原因で正しくない勾配関数がパスする可能性のある点からチェックを保護しようとするものです。

例: randn(5,1)

データ型: double
複素数のサポート: あり

`options` — 有限差分オプション
`optimoptions` の出力

有限差分オプション。optimoptions の出力として指定されます。有限差分に影響するオプションは次のとおりです。

オプション	説明
`FiniteDifferenceStepSize`	有限差分のスカラーまたはベクトルのステップサイズファクター。`FiniteDifferenceStepSize` をベクトル `v` に設定すると、前方有限差分 `delta` は `delta = v.sign′(x).max(abs(x),TypicalX);` ここで、`sign′(0) = 1` を除き `sign′(x) = sign(x)` です。中心有限差分法では `delta = v.*max(abs(x),TypicalX);` スカラー `FiniteDifferenceStepSize` はベクトルに拡張します。既定値は、前進有限差分法では `sqrt(eps)`、中心有限差分法では `eps^(1/3)` です。
`FiniteDifferenceType`	勾配推定に使用される有限差分は `"forward"` (既定の設定) または `"central"` (中心) のいずれかです。`"central"` では 2 倍の関数評価が必要になりますが、一般的に正確性が増します。
`TypicalX`	典型的な `x` の値です。`TypicalX` の要素数は、開始点 `x0` の要素数と等しくなります。既定値は `ones(numberofvariables,1)` です。
DiffMaxChange (非推奨)	有限差分勾配を計算する場合に変数内で生じる最大変化量です (正のスカラー)。既定値は `Inf` です。
DiffMinChange (非推奨)	有限差分勾配を計算する場合に変数内で生じる最小変化量です (非負のスカラー)。既定値は `0` です。

例: optimoptions("fmincon",FiniteDifferenceStepSize=1e-4)

名前と値の引数

すべて折りたたむ

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: IsConstraint=true,Tolerance=5e-4

`Display` — コマンドラインに結果を表示するフラグ
`"off"` (既定値) | `"on"`

コマンドラインに結果を表示するフラグ。"off" (結果を表示しない) または "on" (結果を表示する) として指定します。

例: "off"

データ型: char | string

`IsConstraint` — 非線形制約勾配を確認するフラグ
`false` (既定値) | `true`

非線形制約勾配を確認するフラグ。false (関数は目的関数である) または true (関数は非線形制約関数である) として指定します。

例: true

データ型: logical

`Tolerance` — 勾配の近似の許容誤差
`1e-6` (既定値) | 非負のスカラー

勾配の近似の許容誤差。非負のスカラーとして指定します。戻り値 valid は、fun の勾配とその有限差分近似の絶対相対差が Tolerance 以下である各要素について true です。

例: 1e-3

データ型: double

出力引数

すべて折りたたむ

`valid` — 有限差分近似が勾配と一致することを示す指標
logical スカラー | 2 要素の logical ベクトル

有限差分近似が勾配と一致することを示す指標。目的関数の場合は logical スカラー、非線形制約関数 [c,ceq] の場合は 2 要素の logical ベクトルとして返されます。戻り値 valid は、勾配のすべての要素について、fun の勾配とその有限差分近似の絶対相対差が Tolerance 以下である場合は true です。それ以外の場合、valid は false です。

非線形制約 c または ceq が空の場合、その制約の valid の戻り値は true です。

`err` — 勾配と有限差分近似の相対差
構造体

勾配と有限差分近似の相対差。構造体として返されます。目的関数の場合、フィールド名は Objective です。非線形制約関数の場合、フィールド名は Inequality (c に対応) および Equality (ceq に対応) です。err の各要素は、fun で指定された微分と同じ形状になります。

詳細

すべて折りたたむ

CheckGradients の失敗

初期点の近くで推定された勾配またはヤコビアンが、既定の許容誤差 1e-6 または checkGradients 関数の場合は指定された Tolerance 値内で、指定された微分と一致しませんでした。

通常、この失敗は、目的関数または非線形制約関数の微分計算が正しくないことを意味します。示された微分を改めて確認してください。
場合によっては、微分に対する有限差分近似が不正確であるために失敗することがあります。この不正確性は、関数 (目的または非線形制約) の 2 階微分が大きい場合に生じることがあります。また、既定の 'forward' 有限差分を使用する場合にも生じることがあります。この有限差分は 'central' 有限差分と比べて正確性の面で劣りますが、高速です。微分関数が正しいと考えられる場合は、次のいずれかまたは両方を試して CheckGradients がパスするかどうかを確認してください。
- FiniteDifferenceType オプションを 'central' に設定。
- FiniteDifferenceStepSize オプションを 1e-10 などの小さい値に設定。
微分は初期点の近くのランダムな点でチェックされます。そのため、近傍点ごとにチェック結果が異なる場合、勾配チェックはランダムにパスしたり失敗したりする可能性があります。

詳細については、勾配またはヤコビアンの有効性を確認を参照してください。

バージョン履歴

R2023b で導入

参考

トピック

勾配またはヤコビアンの有効性を確認

checkGradients

構文

説明

例

目的関数の勾配の確認

最小二乗目的関数の勾配の確認

有限差分オプションの変更

非線形制約の勾配の確認

勾配と有限差分近似の差の確認

lsqcurvefit の勾配の確認

入力引数

fun — 確認する関数 関数ハンドル

x0 — 勾配を確認する位置 double 配列 | 1 行 2 列の cell 配列

options — 有限差分オプション optimoptions の出力

名前と値の引数

Display — コマンド ラインに結果を表示するフラグ "off" (既定値) | "on"

IsConstraint — 非線形制約勾配を確認するフラグ false (既定値) | true

Tolerance — 勾配の近似の許容誤差 1e-6 (既定値) | 非負のスカラー

出力引数

valid — 有限差分近似が勾配と一致することを示す指標 logical スカラー | 2 要素の logical ベクトル

err — 勾配と有限差分近似の相対差 構造体

詳細

CheckGradients の失敗

バージョン履歴

参考

トピック

`lsqcurvefit` の勾配の確認

`fun` — 確認する関数
関数ハンドル

`x0` — 勾配を確認する位置
double 配列 | 1 行 2 列の cell 配列

`options` — 有限差分オプション
`optimoptions` の出力

`Display` — コマンドラインに結果を表示するフラグ
`"off"` (既定値) | `"on"`

`IsConstraint` — 非線形制約勾配を確認するフラグ
`false` (既定値) | `true`

`Tolerance` — 勾配の近似の許容誤差
`1e-6` (既定値) | 非負のスカラー

`valid` — 有限差分近似が勾配と一致することを示す指標
logical スカラー | 2 要素の logical ベクトル

`err` — 勾配と有限差分近似の相対差
構造体