polarscatter
Scatter chart in polar coordinates
Syntax
Description
Vector and Matrix Data
polarscatter( plots
theta,rho)theta versus rho and displays a
circular marker at each data point. Specify theta in radians.
To plot one set of points, specify
thetaandrhoas vectors of equal length.To plot multiple sets of points within the same polar axes, specify at least one of
thetaorrhoas a matrix.
polarscatter(___,
sets the marker symbol. For example, mkr)'+' displays cross
markers. Specify the marker symbol after any of the input argument combinations
in the previous syntaxes.
polarscatter(___,'filled') fills the marker
interiors.
Table Data
polarscatter(
plots the variables tbl,thetavar,rhovar)thetavar and rhovar
from the table tbl. To plot one data set, specify one
variable for thetavar and one variable for
rhovar. To plot multiple data sets, specify multiple
variables for thetavar, rhovar, or both.
If both arguments specify multiple variables, they must specify the same number
of variables. (Since R2021b)
Additional Options
polarscatter(
plots into the polar axes specified by pax,___)pax instead of into
the current axes.
polarscatter(___, modifies
the appearance of the scatter plot using one or more name-value pair
arguments. For example, you can use semi-transparent markers by specifying Name,Value)'FaceAlpha' and
a scalar value between 0 and 1.
ps = polarscatter(___)Scatter object or an array of
Scatter objects.. Use ps to modify the
appearance of the Scatter object after it is
created. For a list of properties, see Scatter Properties.
Examples
Create Scatter Chart
Create a scatter chart in polar coordinates.
th = pi/4:pi/4:2*pi; r = [19 6 12 18 16 11 15 15]; polarscatter(th,r)
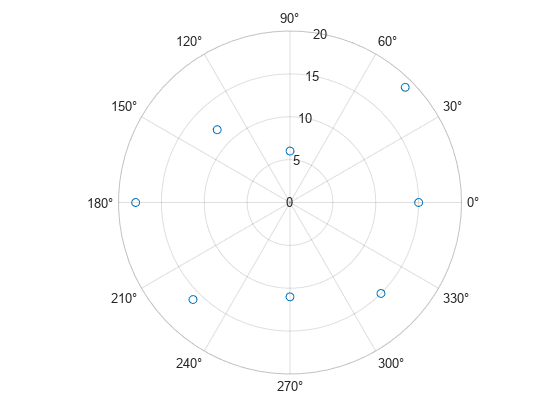
Before R2022a, polar axes do not include degree symbols by default. To add them, get the polar axes using pax = gca. Then modify the tick labels using pax.ThetaTickLabel = string(pax.ThetaTickLabel) + char(176).
Use Filled Markers and Set Marker Size
Create a scatter chart that uses filled markers by specifying the optional input argument, 'filled'. Set the marker size to 75 points squared.
th = linspace(0,2*pi,20);
r = rand(1,20);
sz = 75;
polarscatter(th,r,sz,'filled')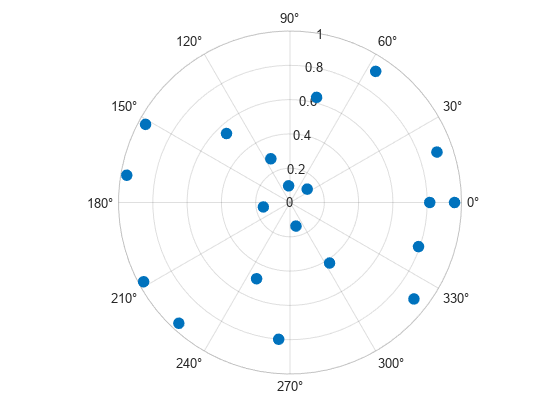
Use Markers with Varying Sizes and Colors
Create a scatter chart with markers of varying sizes and colors. Specify the optional size and color input arguments as vectors. Use unique values in the color vector to specify the different colors you want. The values map to colors in the colormap.
th = pi/4:pi/4:2*pi; r = [19 6 12 18 16 11 15 15]; sz = 100*[6 15 20 3 15 3 6 40]; c = [1 2 2 2 1 1 2 1]; polarscatter(th,r,sz,c,'filled','MarkerFaceAlpha',.5)
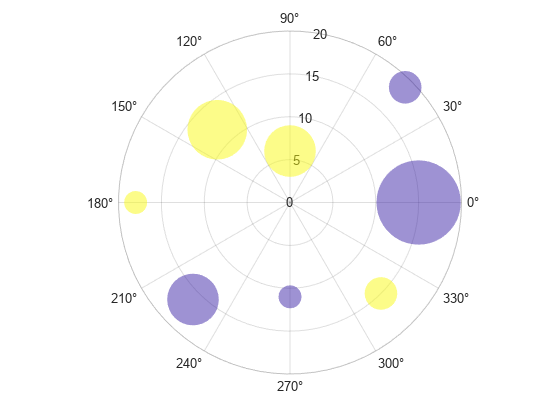
Convert from Degrees to Radians Before Plotting
Create data where the angle values are in degrees. Since polarscatter requires angle values in radians, convert the values to radians before plotting using deg2rad.
th = linspace(0,360,50); r = 0.005*th/10; th_radians = deg2rad(th); polarscatter(th_radians,r)
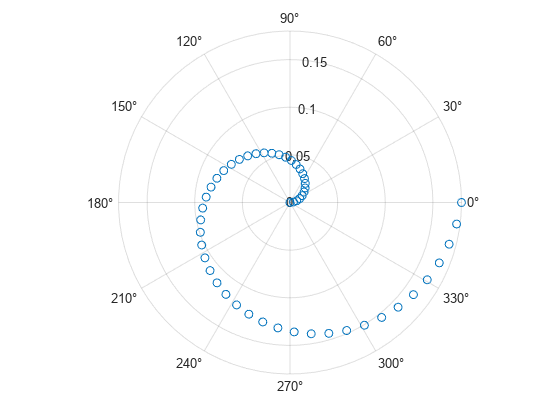
Combine Two Scatter Charts
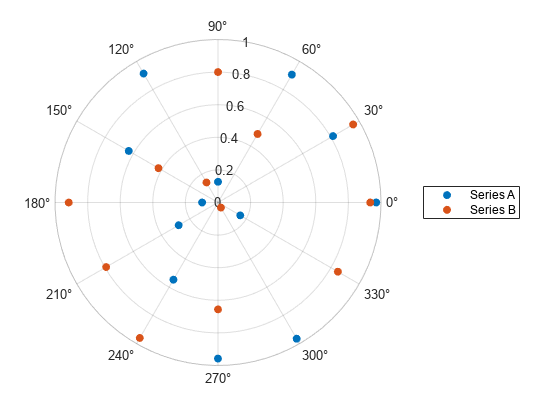
Combine two scatter charts in the same polar axes using the hold command. Add a legend with a description of each chart.
th = pi/6:pi/6:2*pi; r1 = rand(12,1); polarscatter(th,r1,'filled') hold on r2 = rand(12,1); polarscatter(th,r2,'filled') hold off legend('Series A','Series B')
Modify Scatter Chart After Creation
Create a scatter chart and assign the scatter object to the variable ps.
th = pi/6:pi/6:2*pi;
r = rand(12,1);
ps = polarscatter(th,r,'filled')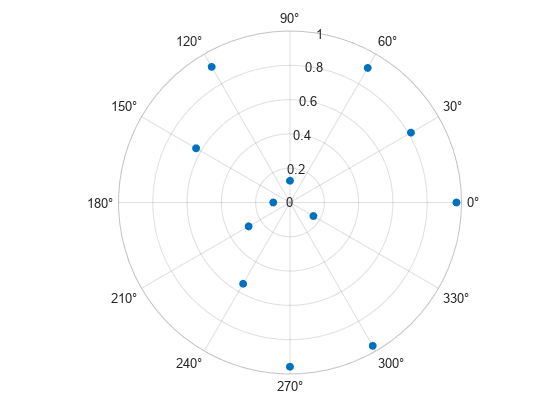
ps =
Scatter with properties:
Marker: 'o'
MarkerEdgeColor: 'none'
MarkerFaceColor: 'flat'
LineWidth: 0.5000
ThetaData: [0.5236 1.0472 1.5708 2.0944 2.6180 3.1416 3.6652 4.1888 4.7124 5.2360 5.7596 6.2832]
RData: [0.8147 0.9058 0.1270 0.9134 0.6324 0.0975 0.2785 0.5469 0.9575 0.9649 0.1576 0.9706]
ZData: [1x0 double]
SizeData: 36
CData: [0 0.4470 0.7410]
Use GET to show all properties
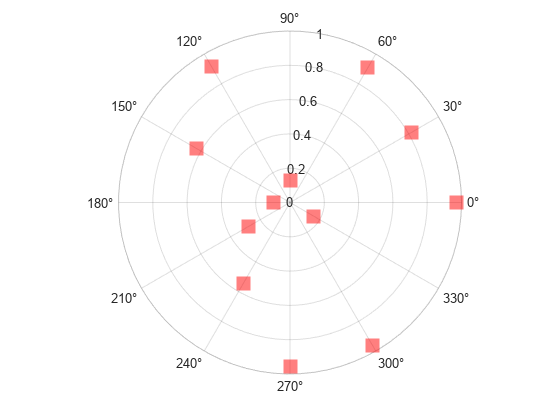
Use ps to modify properties of the scatter object after it is created.
ps.Marker = 'square'; ps.SizeData = 200; ps.MarkerFaceColor = 'red'; ps.MarkerFaceAlpha = .5;
Plot Data from a Table
Since R2021b
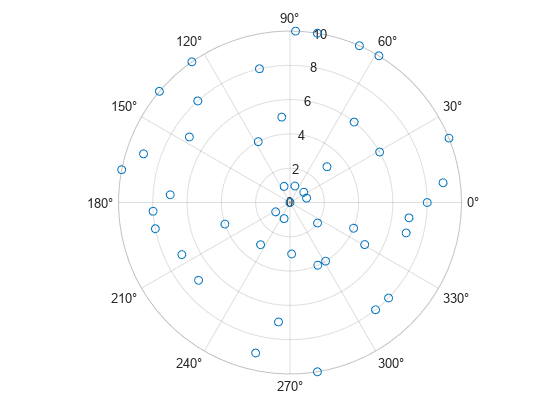
A convenient way to plot data from a table is to pass the table to the polarscatter function and specify the variables you want to plot. For example, create a table with three variables, and plot the 'Th' and 'R1' variables.
% Create a table of random numbers Th = linspace(0,2*pi,50)'; R1 = randi([0 10],50,1); R2 = randi([20 30],50,1); tbl = table(Th,R1,R2); % Create polar scatter chart polarscatter(tbl,'Th','R1')
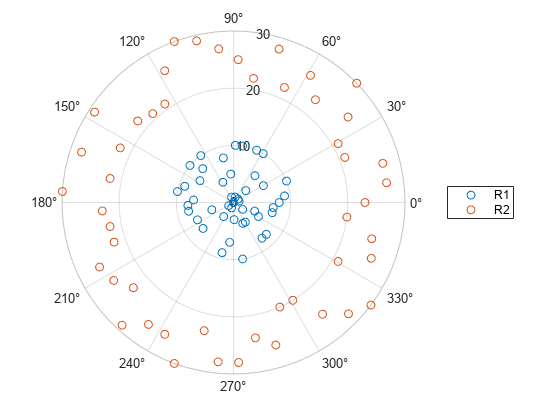
You can also plot multiple variables at the same time. For example, plot two sets of radius values by specifying the rhovar argument as the cell array {'R1','R2'}. Then add a legend. The legend labels match the variable names.
polarscatter(tbl,'Th',{'R1','R2'}) legend
Plot Table Data with Custom Marker Sizes and Colors
Since R2021b
One way to plot data from a table and customize the colors and marker sizes is to set the ColorVariable and SizeData properties. You can set these properties as name-value arguments when you call the polarscatter function, or you can set them on the Scatter object later.
For example, create a table with three variables of random numbers, and plot the Th and R variables with filled markers. Vary the marker colors by specifying the ColorVariable name-value argument. Return the Scatter object as s, so you can set other properties later.
Th = linspace(0,2*pi,50)'; R = randi([0 10],50,1); Colors = rand(50,1); tbl = table(Th,R,Colors); s = polarscatter(tbl,'Th','R','filled','ColorVariable','Colors');
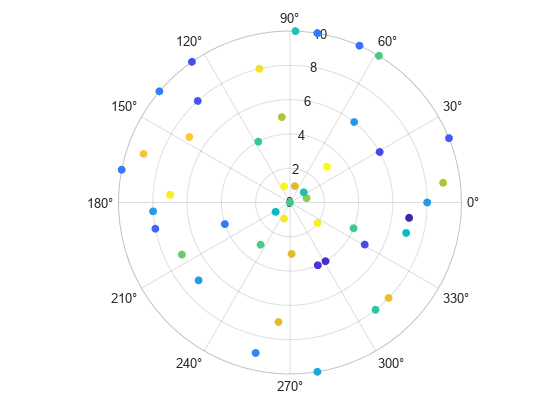
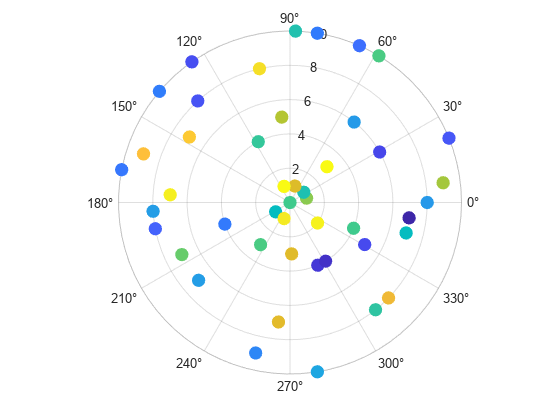
Change the marker sizes to 100 points by setting the SizeData property.
s.SizeData = 100;
Input Arguments
theta — Theta values
scalar | vector | matrix
Theta values, specified as a scalar, vector, or matrix. The ThetaData property
of the scatter object stores the theta values.
The size and shape of theta depends on the shape of
your data. This table describes the most common situations.
| Type of Plot | How to Specify Coordinates |
|---|---|
| Single point | Specify polarscatter(pi/2,0.5) |
| One set of points | Specify polarscatter([0 pi/4 pi/2],[1; 2; 3]) |
| Multiple sets of points that are different colors | If all the sets share the same theta or rho values, specify the shared coordinates as a vector and the other coordinates as a matrix. The length of the vector must match one of the dimensions of the matrix. For example: polarscatter([0 pi/4 pi/2],[4 5 6; 7 8 9]) polarscatter plots a separate
set of points for each column in the
matrix.Alternatively, specify
polarscatter([0 pi/6 pi/2; pi/8 pi/4 pi],[1 2 3; 4 5 6]) |
To convert degrees to radians, use deg2rad.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
rho — Rho values
scalar | vector | matrix
Rho values, specified as a scalar, vector, or matrix. The RData property of the
scatter object stores the rho values.
The size and shape of rho depends on the shape of your
data. This table describes the most common situations.
| Type of Plot | How to Specify Coordinates |
|---|---|
| Single point | Specify polarscatter(pi/2,0.5) |
| One set of points | Specify polarscatter([0 pi/4 pi/2],[1; 2; 3]) |
| Multiple sets of points that are different colors | If all the sets share the same theta or rho values, specify the shared coordinates as a vector and the other coordinates as a matrix. The length of the vector must match one of the dimensions of the matrix. For example: polarscatter([0 pi/4 pi/2],[4 5 6; 7 8 9]) polarscatter plots a separate
set of points for each column in the
matrix.Alternatively, specify
polarscatter([0 pi/6 pi/2; pi/8 pi/4 pi],[1 2 3; 4 5 6]) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
sz — Marker size
36 (default) | numeric scalar | row or column vector | matrix | []
Marker size, specified as a numeric scalar, vector, matrix, or empty array
([]). The size controls the area of each marker in
points squared. An empty array specifies the default size of 36 points. The
way you specify the size depends on how you specify theta
and rho, and how you want the plot to look. This table
describes the most common situations.
| Desired Marker Sizes | theta and rho
| sz | Example |
|---|---|---|---|
Same size for all points | Any valid combination of vectors or matrices
described for | Scalar | Specify th = [0 pi/6 pi/2]; r = [1 2; 2 4; 5 6]; polarscatter(th,r,100) |
Different size for each point | Vectors of the same length |
| Specify th = [0 pi/6 pi/2]; r = [1; 2; 3]; sz = [50 500 100]; polarscatter(th,r,sz) Specify
th = [0 pi/6 pi/2]; r = [1; 2; 3]; sz = [50 500 100; 300 1000 200]; polarscatter(th,r,sz) |
Different size for each point | At least one of |
| Specify th = [0 pi/6 pi/2]; r = [1 2; 2 4; 5 6]; sz = [50 500 1000]; polarscatter(th,r,sz) Specify
th = [0 pi/6 pi/2]; r = [1 2; 2 4; 5 6]; sz = [50 500; 1000 2000; 100 300]; polarscatter(th,r,sz) |
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
c — Marker colors
color name | RGB triplet | matrix of RGB triplets | vector of colormap indices
Marker color, specified as a color name, RGB triplet, matrix of RGB triplets, or a vector of colormap indices.
Color name — A color name such as
'red', or a short name such as'r'.RGB triplet — A three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1]; for example,[0.4 0.6 0.7]. RGB triplets are useful for creating custom colors.Matrix of RGB triplets — A three-column matrix in which each row is an RGB triplet.
Vector of colormap indices — A vector of numeric values that is the same length as the
thetaandrhovectors.
The way you specify the color depends on the desired color scheme and whether you are plotting one set of coordinates or multiple sets of coordinates. This table describes the most common situations.
| Color Scheme | How to Specify the Color | Example |
|---|---|---|
Use one color for all the points. | Specify a color name or a short name from the table below, or specify one RGB triplet. | Plot one set of points, and specify the color
as th = [0 pi/6 pi/2];
r = [1 2 3];
c = 'red';
polarscatter(th,r,[],c)Plot two sets of points, and specify the color as red using an RGB triplet. th = [0 pi/6 pi/2]; r = [1 2; 2 4; 5 6]; c = [1 0 0]; polarscatter(th,r,[],c) |
Assign different colors to each point using a colormap. | Specify a row or column vector of numbers. The numbers index into the current colormap array. The smallest value maps to the first row in the colormap, and the largest value maps to the last row. The intermediate values map linearly to the intermediate rows. If your plot has three points, specify a column vector to ensure the values are interpreted as colormap indices. You can use this method only
when | Create a vector th = [0 pi/6 pi/2 2*pi/3];
r = [1 2 3 4];
c = [1 2 3 4];
polarscatter(th,r,[],c)
colormap(gca,'winter') |
Create a custom color for each point. | Specify an m-by-3 matrix of RGB triplets, where m is the number of points in the plot. You can use this method only when
| Create a matrix th = [0 pi/6 pi/2 2*pi/3]; r = [1 2 3 4]; c = [1 0 0; 0 1 0; 0 0 1; 0 0 0]; polarscatter(th,r,[],c) |
Create a different color for each data set. | Specify an n-by-3 matrix of RGB triplets, where n is the number of data sets. You can
use this method only when at least one of
| Create a matrix th = [0 pi/6 pi/2]; r = [1 2; 2 4; 5 6]; c = [1 0 0; 0 0 1]; polarscatter(th,r,[],c) |
Color Names and RGB Triplets for Common Colors
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB® uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] | "#0072BD" |
|
[0.8500 0.3250 0.0980] | "#D95319" |
|
[0.9290 0.6940 0.1250] | "#EDB120" |
|
[0.4940 0.1840 0.5560] | "#7E2F8E" |
|
[0.4660 0.6740 0.1880] | "#77AC30" |
|
[0.3010 0.7450 0.9330] | "#4DBEEE" |
|
[0.6350 0.0780 0.1840] | "#A2142F" |
|
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | char | string
mkr — Marker symbol
'o' (default) | '+' | '*' | '.' | 'x' | 's' | ...
Marker symbol, specified as one of the marker symbols listed in this table.
| Marker | Description | Resulting Marker |
|---|---|---|
"o" | Circle |
|
"+" | Plus sign |
|
"*" | Asterisk |
|
"." | Point |
|
"x" | Cross |
|
"_" | Horizontal line |
|
"|" | Vertical line |
|
"square" | Square |
|
"diamond" | Diamond |
|
"^" | Upward-pointing triangle |
|
"v" | Downward-pointing triangle |
|
">" | Right-pointing triangle |
|
"<" | Left-pointing triangle |
|
"pentagram" | Pentagram |
|
"hexagram" | Hexagram |
|
The Marker property of the scatter object
stores the marker symbol.
tbl — Source table
table | timetable
Source table containing the data to plot, specified as a table or a timetable.
thetavar — Table variables containing theta values
one or more table variable indices
Table variables containing the theta values, specified as one or more table variable indices.
Specifying Table Indices
Use any of the following indexing schemes to specify the desired variable or variables.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
Plotting Your Data
The table variables you specify can contain any numeric data type.
To plot one data set, specify one variable for thetavar and one variable
for rhovar. For example, create a table with three variables. Plot the
Th and R1
variables.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R1 = randi([0 10],10,1); R2 = randi([20 30],10,1); tbl = table(Th,R1,R2); % Create polar scatter chart polarscatter(tbl,'Th','R1')
To plot multiple data sets together, specify multiple variables for
thetavar, rhovar, or both. If you specify multiple
variables for both arguments, the number of variables for each argument must be the
same.
For example, plot the Th variable on the theta-axis
and the R1 and R2 variables on the
r-axis.
polarscatter(tbl,'Th',{'R1','R2'})
You can also use different indexing schemes for the table variables. For example, specify
thetavar as a variable name and rhovar as an index
number.
polarscatter(tbl,'Th',2)rhovar — Table variables containing rho values
one or more table variable indices
Table variables containing the rho values, specified as one or more table variable indices.
Specifying Table Indices
Use any of the following indexing schemes to specify the desired variable or variables.
| Indexing Scheme | Examples |
|---|---|
Variable names:
|
|
Variable index:
|
|
Variable type:
|
|
Plotting Your Data
The table variables you specify can contain any numeric data type.
To plot one data set, specify one variable for thetavar and one variable
for rhovar. For example, create a table with three variables. Plot the
Th and R1
variables.
% Create a table of random numbers Th = linspace(0,2*pi,10)'; R1 = randi([0 10],10,1); R2 = randi([20 30],10,1); tbl = table(Th,R1,R2); % Create polar scatter chart polarscatter(tbl,'Th','R1')
To plot multiple data sets together, specify multiple variables for
thetavar, rhovar, or both. If you specify multiple
variables for both arguments, the number of variables for each argument must be the
same.
For example, plot the Th variable on the theta-axis
and the R1 and R2 variables on the
r-axis.
polarscatter(tbl,'Th',{'R1','R2'})
You can also use different indexing schemes for the table variables. For example, specify
thetavar as a variable name and rhovar as an index
number.
polarscatter(tbl,'Th',2)pax — PolarAxes object
PolarAxes object
PolarAxes object. If you do not specify the
polar axes, then polarscatter uses the current
axes. polarscatter does not support plotting into
Cartesian axes.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: polarscatter(th,r,'filled','MarkerFaceAlpha',.5) creates
filled, semi-transparent markers.
The scatter object properties listed here are only a subset. For a complete list, see Scatter Properties.
MarkerFaceAlpha — Marker face transparency
1 (default) | scalar in range [0,1]
Marker face transparency, specified as a scalar in the range [0,1].
A value of 1 is opaque and 0 is transparent. Values between 0 and
1 are semi-transparent.
MarkerEdgeColor — Marker outline color
"flat" (default) | RGB triplet | hexadecimal color code | "r" | "g" | "b" | ...
Marker outline color, specified "flat", an RGB triplet, a hexadecimal color
code, a color name, or a short name. The default value of "flat" uses
colors from the CData property.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] | "#0072BD" |
|
[0.8500 0.3250 0.0980] | "#D95319" |
|
[0.9290 0.6940 0.1250] | "#EDB120" |
|
[0.4940 0.1840 0.5560] | "#7E2F8E" |
|
[0.4660 0.6740 0.1880] | "#77AC30" |
|
[0.3010 0.7450 0.9330] | "#4DBEEE" |
|
[0.6350 0.0780 0.1840] | "#A2142F" |
|
Example: [0.5 0.5 0.5]
Example: "blue"
Example: "#D2F9A7"
MarkerFaceColor — Marker fill color
"none" (default) | "flat" | "auto" | RGB triplet | hexadecimal color code | "r" | "g" | "b" | ...
Marker fill color, specified as "flat", "auto", an RGB
triplet, a hexadecimal color code, a color name, or a short name. The
"flat" option uses the CData values. The
"auto" option uses the same color as the
Color property for the axes.
For a custom color, specify an RGB triplet or a hexadecimal color code.
An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range
[0,1], for example,[0.4 0.6 0.7].A hexadecimal color code is a string scalar or character vector that starts with a hash symbol (
#) followed by three or six hexadecimal digits, which can range from0toF. The values are not case sensitive. Therefore, the color codes"#FF8800","#ff8800","#F80", and"#f80"are equivalent.
Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.
| Color Name | Short Name | RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan"
| "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | Not applicable | Not applicable | Not applicable | No color |
Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.
| RGB Triplet | Hexadecimal Color Code | Appearance |
|---|---|---|
[0 0.4470 0.7410] | "#0072BD" |
|
[0.8500 0.3250 0.0980] | "#D95319" |
|
[0.9290 0.6940 0.1250] | "#EDB120" |
|
[0.4940 0.1840 0.5560] | "#7E2F8E" |
|
[0.4660 0.6740 0.1880] | "#77AC30" |
|
[0.3010 0.7450 0.9330] | "#4DBEEE" |
|
[0.6350 0.0780 0.1840] | "#A2142F" |
|
Example: [0.3 0.2 0.1]
Example: "green"
Example: "#D2F9A7"
LineWidth — Width of marker edge
0.5 (default) | positive value
Width of marker edge, specified as a positive value in point units.
Example: 0.75
ColorVariable — Table variable containing color data
table variable index
Table variable containing the color data, specified as a variable index into the source table.
Specifying the Table Index
Use any of the following indexing schemes to specify the desired variable.
| Indexing Scheme | Examples |
|---|---|
Variable name:
|
|
Variable index:
|
|
Variable type:
|
|
Specifying Color Data
Specifying the ColorVariable property controls the colors of the markers.
The data in the variable controls the marker fill color when the
MarkerFaceColor property is set to
"flat". The data can also control the marker outline color,
when the MarkerEdgeColor is set to
"flat".
The table variable you specify can contain values of any numeric type. The values can be in either of the following forms:
A column of numbers that linearly map into the current colormap.
A three-column array of RGB triplets. RGB triplets are three-element vectors whose values specify the intensities of the red, green, and blue components of specific colors. The intensities must be in the range
[0,1]. For example,[0.5 0.7 1]specifies a shade of light blue.
When you set the ColorVariable property, MATLAB updates the CData property.
Version History
Introduced in R2016bR2022b: Plots created with tables preserve special characters in legend labels
When you pass a table and one or more variable names to the polarscatter function, the legend labels now display any special characters that are included in the table variable names, such as underscores. Previously, special characters were interpreted as TeX or LaTeX characters.
For example, if you pass a table containing a variable named Sample_Number
to the polarscatter function and then display a legend, the
underscore appears in the legend label. In R2022a and earlier releases, the
underscore is interpreted as a subscript.
| Release | Label for Table Variable "Sample_Number" |
|---|---|
R2022b |
|
R2022a |
|
To display legend labels with TeX or LaTeX formatting, call the legend
function with the desired label strings after plotting. For example:
legend(["Sample_Number" "Another_Legend_Label"])
R2021b: Pass tables directly to polarscatter
Create plots by passing a table to the polarscatter function followed by the variables you want to plot. When you specify your data as a table, the axis labels and the legend (if present) are automatically labeled using the table variable names.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)