磁気浮上システムのバッチ線形化の結果からの LPV モデル
この例では、磁気浮上システムのバッチ線形化の結果から非線形モデルの線形パラメーター変動モデルを取得する方法を示します。この非線形モデルは磁気浮上システムの LPV モデルの例で記述されています。
この例では、次を行います。
平衡点のグリッドで非線形の Simulink® モデルを線形化します。
LTI モデルと平衡オフセットのグリッド配列から LPV モデルを作成します。
平衡点のグリッドでコントローラーを設計します。このグリッドは、線形化に使用されるグリッドとは異なる場合があります。
コマンド ラインの LTI シミュレーション (固定の操作点) と LPV シミュレーション (パラメーターの軌跡を指定) を使用してコントローラーをテストします。
Simulink の非線形プラントでコントローラーをテストします。
モデル パラメーター
Simulink モデルを開きます。
open_system('MaglevOpenLoop.slx')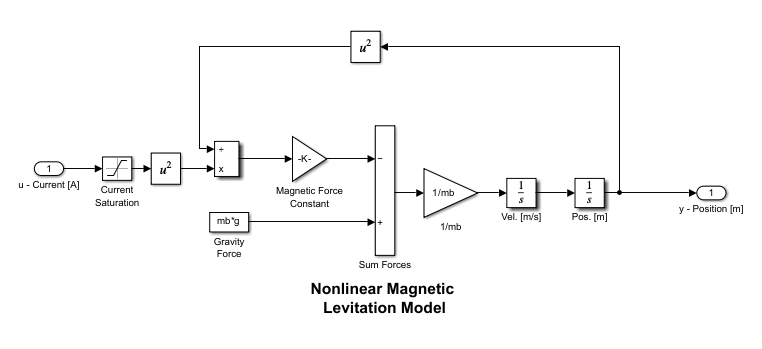
モデルのパラメーターを指定します。
mb = 0.02; g = 9.81; alpha = 2.4832e-5; umin = -inf; umax = inf;
バッチ平衡化と線形化
5 つの異なる高さ値として平衡化条件を指定します (,) = (,0)。
Ns = 5; hmin = 0.05; hmax = 0.25; hs = linspace(hmin,hmax,Ns);
操作点の仕様を作成します。
clear opspec; for i=1:Ns % Set states to desired equilibrium values h0 = hs(i); hdot0 = 0; % Initialize operating point specification opspec(i) = operspec('MaglevOpenLoop'); % Position: h=hs(i) opspec(i).States(1).Known = 1; opspec(i).States(1).SteadyState = 1; % Velocity: hdot=0 opspec(i).States(2).Known = 1; opspec(i).States(2).SteadyState = 1; % Input current: Restrict u>=0 opspec(i).Inputs.Min=0; end
操作点を検出します。
opt = findopOptions('DisplayReport','off', 'OptimizerType','graddescent-proj'); [op,report] = findop('MaglevOpenLoop',opspec,opt);
線形化を計算します。
io = [linio('MaglevOpenLoop/u - Current [A]',1,'in'); % u linio('MaglevOpenLoop/Magnetic Levitation Plant Model',1,'out')]; % y linOpt = linearizeOptions('StoreOffsets',true); [G,~,info] = linearize('MaglevOpenLoop',op,io,linOpt); G.u = 'u'; G.y = 'y'; G.SamplingGrid = struct('h',hs);
ssInterpolant を使用して LPV モデルを作成します。
offsets = info.Offsets; Glpv = ssInterpolant(G,offsets);
バッチ PID 調整
コントローラーのグリッドは、それが可能であることを示すために、モデルに使用されるものよりも粗くなります。また、コントローラーのグリッド化はコントローラー設計を簡略化するために粗い (グリッド点が少ない) ことが多く、一方で解析とシミュレーションには細かいグリッド化で忠実度の高い LPV モデルを使用できます。
Ncd = 3; hcd = linspace(hmin,hmax,Ncd);
(,) に対応する理想的な 2 次応答として Tideal を定義します。
wn = 30; zeta = 0.7; Tideal = tf(wn^2,[1 2*zeta*wn wn^2]);
pidtune を使用してゲイン スケジュール PID コントローラーを調整します。
wc = 50;
[Ga,Goffsets] = sample(Glpv,[],hcd);
Ka = pidtune(Ga,'pid',wc);
Ka.Tf = 0.001;
Ka.SamplingGrid.h = hcd;次の方程式をもつ LPV コントローラーを作成します。
ここで、 は高さ に対する平衡電流です。このコントローラーは、この平衡値近くに電流を調整します。
Koffsets = struct('u',0,'y',{Goffsets.u}); Ka = ss(Ka); Klpv = ssInterpolant(Ka,Koffsets);
LTI の解析
閉ループ モデルのステップ応答をシミュレートし、Tideal と比較します。
figure(1); Tf = 0.5; Tlpv = feedback(Glpv*Klpv,1); step(sample(Tlpv,[],hs),'b',Tideal,'r--',Tf); grid on; legend('Tlpv','Tideal');
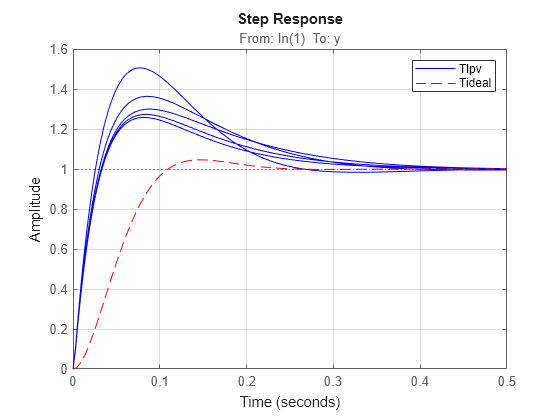
閉ループ システムには、理想的な応答である Tideal にはない追加のゼロがあります。これらのゼロは PID コントローラーから生じるもので、これによって立ち上がり時間が短くなり、オーバーシュートが大きくなっています。
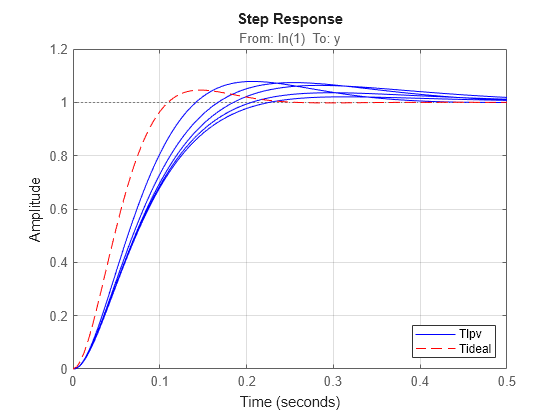
基準プレフィルター Fref を使用した 2 自由度のアーキテクチャを使用することで、オーバーシュートを低減できます。簡単にするために、プレフィルターを LTI システムとしてモデル化します。
Fref = ss(-10,10,1,0); figure(2); Tf = 0.5; step(sample(Tlpv*Fref,[],hs),'b',Tideal,'r--',Tf); grid on; legend('Tlpv','Tideal','Location','Southeast');
LPV と非線形のシミュレーションの比較
ゲイン スケジュール PID で非線形応答をシミュレートします。MaglevClosedLoop.slx モデルでは、コントローラーに LPV System ブロックを使用しています。
初期条件を指定し、モデルをシミュレートします。
h0 = (hmin+hmax)/2;
hdot0 = 0;
tstep = 0.2;
Tf = 1.2;
hstep0 = h0;
hStepAmp = 0.25*h0;
hstepf = h0+hStepAmp;
sim('MaglevClosedLoop',[0 tstep+Tf]);応答をプロットします。
figure(3); subplot(2,1,1); plot(y.Time,y.Data,'b',r.Time,r.Data,'r--'); ylabel('y, m'); legend('y','r','Location','Southeast'); grid on; subplot(2,1,2); plot(u.Time,u.Data); ylabel('u, A'); xlabel('t, sec'); grid on;
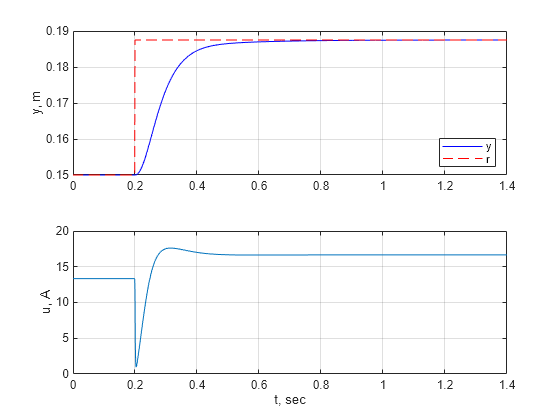
結果を LPV シミュレーションと比較します。
CL = Tlpv*Fref;
を "理想的" な軌跡に設定し、ステップ応答をシミュレートします。
t = linspace(0,tstep+Tf,100); StepConfig = RespConfig('Bias',h0,'Delay',tstep,'Amplitude',hStepAmp); p_ideal = step(Tideal*Fref,t,StepConfig); y1 = step(CL,t,p_ideal,StepConfig);
と設定し、ステップ応答をシミュレートします。
pFcn = @(t,x,u) x(1); StepConfig = RespConfig('Bias',h0,'Delay',tstep,... 'Amplitude',hStepAmp,'InitialParameter',h0); y2 = step(CL,t,pFcn,StepConfig);
応答の比較をプロットします。
figure(4) tsim = y.Time; ysim = y.Data; plot(t,y1,t,y2,tsim,ysim,'k--'); legend('p ideal','p true','Nonlinear','Location','Southeast'); xlim([0 Tf]), grid
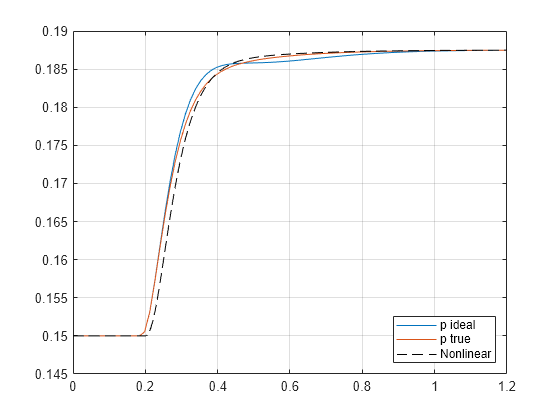
どちらの LPV シミュレーションでも非線形応答がよく近似されています。"実際" の軌跡を使用したシミュレーションの方が、やや優れた近似になっています。
モデルを閉じます。
bdclose('MaglevOpenLoop') bdclose('MaglevClosedLoop')
参考
ssInterpolant | sample | ndgrid | linearize (Simulink Control Design) | step | RespConfig