磁気浮上システムの LPV モデル

この例では、磁気浮上システムの解析的線形パラメーター変動 (LPV) モデルを使用してボールの高さを制御します。この例では、LPV プラント モデルを線形運動方程式から直接作成します。

非線形システム

次の図は、磁気ボール浮上装置とその主要コンポーネントを示しています。ボールに対する磁力を発生させるコイルに電流 $\mathit{i}$ (A) が供給されます。ボールの位置は $\mathit{h}$ (m) で表されます。赤外線センサーでボールの位置 $\mathit{y}$ (V) が測定されます。目的は、目標位置 $\bar{\mathit{h}}$ にボールを浮上させることです。ボールに加わる主な力は、重力による引力 ${\mathit{F}}_{\mathit{g}}$ と磁力 ${\mathit{F}}_{\mathit{m}}$ の 2 つです。

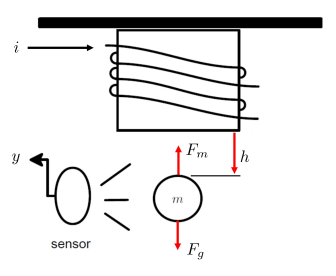
モデルのダイナミクスは次の非線形方程式で定義されます。

$${\mathit{m}}_{\mathit{b}}\ddot{\mathit{h}}={\mathit{m}}_{\mathit{b}}\mathit{g}-\alpha \frac{{\mathit{i}\left(\mathit{t}\right)}^2}{{\mathit{h}\left(\mathit{t}\right)}^2}$$

ここで、以下となります。

• ${\mathit{m}}_{\mathit{b}}$ はボールの質量 (kg) です。

• $\mathit{g}$ は重力加速度 (m/s^2) です。

• $\alpha$ は磁力の定数 (N$\times$m/(A^2)) です。

モデルのパラメーターを定義します。

mb = 0.02;
g = 9.81;
alpha = 2.4832e-5;

平衡条件

ボールの高さ $\bar{\mathit{h}}$ の平衡 (定常状態) 条件は次の方程式で特徴付けられます。

$$0={\mathit{m}}_{\mathit{b}}\mathit{g}-\alpha \frac{{\bar{\mathit{i}}}^2}{{\bar{\mathit{h}}}^2}$$.

この高さを維持するために必要な電流は次のとおりです。

$$\bar{\mathit{i}}=\sqrt{\frac{{\mathit{m}}_{\mathit{b}}\mathit{g}}{\alpha }}\bar{\mathit{h}}$$.

線形運動方程式

このプラントの LPV 近似を作成するには、スケジューリング変数として $\mathit{p}=\bar{\mathit{h}}$ を選択し、$\mathit{p}$ 依存の平衡条件のまわりで運動方程式を線形化します。

$${\mathit{x}}_0\left(\mathit{p}\right)=\left(\begin{array}{c}\bar{\mathit{h}}\\ 0\end{array}\right),{\mathit{u}}_0\left(\mathit{p}\right)=\bar{\mathit{i}}=\sqrt{\frac{{\mathit{m}}_{\mathit{b}}\mathit{g}}{\alpha }}\bar{\mathit{h}},{\mathit{y}}_0\left(\mathit{p}\right)=\bar{\mathit{h}}$$.

これにより、次のような LPV モデルが得られます。

$$\dot{\mathit{x}}=\mathit{A}\left(\mathit{p}\right)\left(\mathit{x}-{\mathit{x}}_0\left(\mathit{p}\right)\right)+\mathit{B}\left(\mathit{p}\right)\left(\mathit{u}-{\mathit{u}}_0\left(\mathit{p}\right)\right)$$

$\mathit{y}={\mathit{y}}_0\left(\mathit{p}\right)+\mathit{C}\left(\mathit{x}-{\mathit{x}}_0\left(\mathit{p}\right)\right)$

ここで次のとおりです。

$$\mathit{x}=\left(\begin{array}{c}\mathit{h}\\ \dot{\mathit{h}}\end{array}\right),\mathit{u}=\mathit{i},\mathit{y}=\mathit{h},\mathit{A}=\left(\begin{array}{cc}0& 1\\ {\mathit{a}}_0\left(\mathit{p}\right)& 0\end{array}\right),\mathit{B}=\left(\begin{array}{c}0\\ {\mathit{b}}_0\left(\mathit{p}\right)\end{array}\right),\mathit{C}=\left(\begin{array}{cc}1& 0\end{array}\right)$$

および

$${\mathit{a}}_0\left(\mathit{p}\right)=\frac{2\mathit{g}}{\mathit{p}},{\mathit{b}}_0\left(\mathit{p}\right)=-2\frac{\sqrt{\mathit{g}\alpha /{\mathit{m}}_{\mathit{b}}}}{\mathit{p}}$$.

このシステムの行列とオフセットは関数 dataFcnMaglev.m で定義されています。

lpvss を使用してモデルを作成します。

Glpv = lpvss('h',@dataFcnMaglev);

ゲイン スケジュール PID コントローラー

PID 調整のために、$\mathit{h}$ の値をいくつか選択し、それらの高さにおける LPV ダイナミクスをサンプリングして局所的な LTI モデルを取得します。

高さの値を 0.05 ～ 0.25 の範囲で 3 つ選択します。

hmin = 0.05;
hmax = 0.25;
hcd = linspace(hmin,hmax,3);
[Ga,Goffsets] = sample(Glpv,[],hcd);
size(Ga)

1x3 array of state-space models.
Each model has 1 outputs, 1 inputs, and 2 states.

$\mathit{h}$ の各値について、pidtune を使用して PID コントローラーを調整します。ターゲット交差周波数は 50 rad/s に設定されています。

wc = 50;
Ka = pidtune(Ga,'pid',wc);
Ka.Tf = 0.001;

次に、ssInterpolant を使用して、$\mathit{h}$ の選択した値の間に調整後のゲインを線形に内挿するゲイン スケジュール PID コントローラーを作成します。このコントローラーでは、フィードフォワード制御として平衡電流 ${\mathit{u}}_0\left(\mathit{p}\right)$ も使用します。これにより、PID でその平衡値近くに電流が調整されるようになります。

Ka.SamplingGrid.h = hcd;
Koffsets = struct('y',{Goffsets.u});
Klpv = ssInterpolant(ss(Ka),Koffsets);

LTI の解析

評価用に、理想的な応答を 2 次システム Tideal としてモデル化します。

wn = 30;
zeta = 0.7;
Tideal = tf(wn^2,[1 2*zeta*wn wn^2]);

より細かい $\mathit{h}$ のグリッドで閉ループ LPV ダイナミクスをサンプリングします。

hs = linspace(hmin,hmax,5);

閉ループ モデルのステップ応答をシミュレートし、Tideal と比較します。

Tlpv = feedback(Glpv*Klpv,1);
step(sample(Tlpv,[],hs),'b',Tideal,'r--',0.5);
grid on
legend('Tlpv','Tideal')

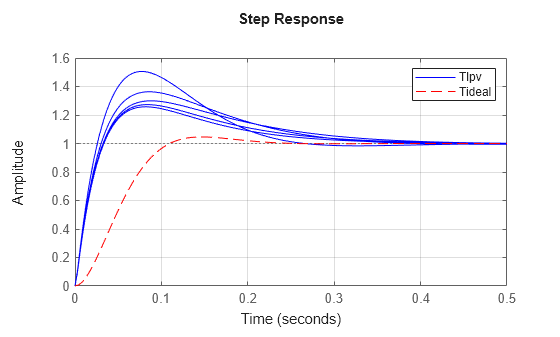
閉ループ システムには、理想的な応答である Tideal にはない追加のゼロがあります。これらのゼロは PID コントローラーから生じるもので、これによって立ち上がり時間が短くなり、オーバーシュートが大きくなっています。

基準プレフィルター Fref を使用した 2 自由度のアーキテクチャを使用することで、オーバーシュートを低減できます。簡単にするために、プレフィルターを LTI システムとしてモデル化します。

Fref = ss(-10,10,1,0);
step(sample(Tlpv*Fref,[],hs),'b',Tideal,'r--',0.5);
grid on;
legend('Tlpv','Tideal','Location','Southeast');

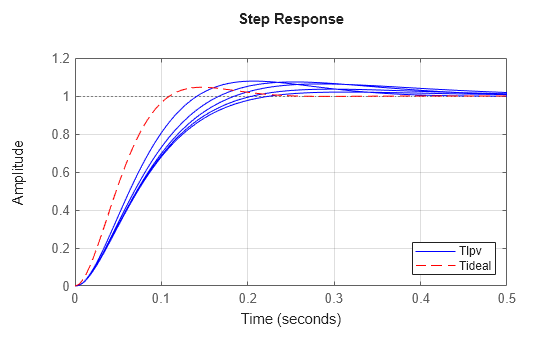
LPV シミュレーション

非線形の閉ループ応答を近似するために、プレフィルターを使用して閉ループ LPV モデルの過渡応答をシミュレートします。これにはパラメーターの軌跡 $\mathit{p}\left(\mathit{t}\right)=\mathit{h}\left(\mathit{t}\right)$ を指定する必要がありますが、これは前もってはわかりません。代わりに、Tideal*Fref で生成される "理想的" な応答に設定できます。

CL = Tlpv*Fref;

初期の高さとステップ信号のパラメーターを設定します。

h0 = (hmin+hmax)/2;
tstep = 0.2;  Tf = 1.2;  hStepAmp = 0.25*h0;

$\mathit{p}\left(\mathit{t}\right)$ を理想的な軌跡に設定し、応答をシミュレートします。

t = linspace(0,tstep+Tf,100);
StepConfig = RespConfig('Bias',h0,'Delay',tstep,'Amplitude',hStepAmp);
p_ideal = step(Tideal*Fref,t,StepConfig);
y1 = step(CL,t,p_ideal,StepConfig);

あるいは、"実際" の軌跡を使用する場合は、$\mathit{p}\left(\mathit{t}\right)$ を時間 $\mathit{t}$、入力 $\mathit{u}$、および状態 $\mathit{x}$ の関数 $\mathit{F}\left(\mathit{t},\mathit{x},\mathit{u}\right)$ として暗黙的に指定できます。ここで、$\mathit{p}\left(\mathit{t}\right)$ は単に最初の状態です。

$\mathit{p}\left(\mathit{t}\right)=\mathit{h}\left(\mathit{t}\right)$ と設定し、ステップ応答をシミュレートします。

pFcn = @(t,x,u) x(1);
StepConfig = RespConfig('Bias',h0,'Delay',tstep,...
   'Amplitude',hStepAmp,'InitialParameter',h0);
y2 = step(CL,t,pFcn,StepConfig);

2 つの応答をプロットして比較します。

plot(t,y1,t,y2);
legend('p ideal','p true','Location','Southeast');
grid

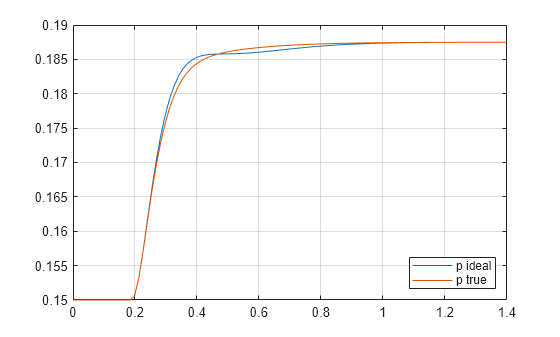
2 つの応答は互いに近くなっています。この例に対応する Simulink ベースの例では、"実際" の軌跡を使用したシミュレーション用の小さいエッジがある両方の LPV シミュレーションで非線形応答がよく近似されています。

プラント データ関数

type dataFcnMaglev.m

function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = dataFcnMaglev(~,p)
% MAGLEV example:
% x = [h ; dh/dt]
% p=hbar (equilibrium height)
mb = 0.02; % kg
g = 9.81;
alpha = 2.4832e-5;
A = [0 1;2*g/p 0];
B = [0 ; -2*sqrt(g*alpha/mb)/p];
C = [1 0];  % h
D = 0;
E = [];
dx0 = [];
x0 = [p;0];
u0 = sqrt(mb*g/alpha)*p;  % ibar
y0 = p;                   % y = h = hbar + (h-hbar)
Delays = [];

参考

lpvss | sample | step | RespConfig

トピック

• LTV モデリングと LPV モデリング
• MATLAB および Simulink での LTV モデルと LPV モデルの使用
• エンジン スロットルの LPV モデル
• ゲイン スケジュール PI コントローラーの解析
• ゲイン スケジュール LQG コントローラー
• ゲイン スケジュール制御の隠れ結合
• 磁気浮上システムのバッチ線形化の結果からの LPV モデル