ゲイン スケジュール LQG コントローラー

ライブ スクリプトを開く

この例では、操作点の変化が速すぎる場合にゲイン スケジュール制御で発生する可能性がある安定性の喪失について説明します。これは、[1] の 102 ページにある例に対応します。[2] の例 5.2.1. に追加の詳細が記載されています。

LPV プラント

LPV プラントは、パラメーター p に依存する 2 次モデルです。システムには、p の固定 (定数) 値に対する減衰率の小さな極が 2 つあります。プラントの方程式は次のとおりです。

(x˙1x˙2)=(01-1-p2-0.2)(x1x2)+(01)u

y=(10)(x1x2)

ここで、パラメーター p は |p|≤1 を満たします。

G = lpvss('p',@GFCN);

"固定" パラメーター値の極を表示します。

pval = -1:0.1:1;
Gs = sample(G,0,pval);
Gpole = pole(Gs);
Gpole = Gpole(:);

plot(real(Gpole),imag(Gpole),'bx');
axis([-0.2 0 -1.5 1.5]);
xlabel('Real');
ylabel('Imag')
grid on;

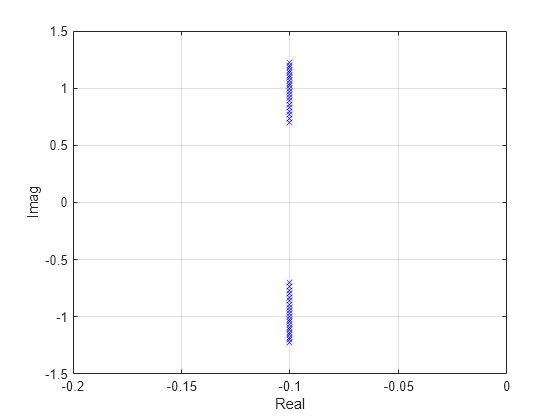
Figure contains an axes object. The axes object with xlabel Real, ylabel Imag contains a line object which displays its values using only markers.

積分動作を含むゲイン スケジュール LQG コントローラー

ゲイン スケジュール線形 2 次ガウシアン (LQG) コントローラーは、状態フィードバックを状態オブザーバーと組み合わせて積分動作を含めます。オブザーバーと状態フィードバック ゲインはループ伝達再生を使用して設計されています。スケジュール コントローラー (積分動作を含む) は、[1] の図 1 の Ka に対応します。

[1] の図 1 で示されているように、入力で積分器を使用してプラントを拡張します。コントローラーで積分器が実装されます。積分動作により、良好な低周波数の追従と一定の外乱の完全な抑制が確保されます。

Gaug = G*tf(1,[1 0]);

関数 KFCN を使用して LPV コントローラーを作成します。この関数は、任意のパラメーター値について、対応するプラントの行列の LQR ゲインとカルマン ゲインを計算します。

Ka = lpvss('p', @(t,p) KFCN(t,p,Gaug));

LTI の解析

固定パラメーター値に対する開ループ応答をプロットします。ループはすべてのパラメーター値で同じであることに注意してください。スケジュール コントローラーは、固定パラメーター値の減衰率の小さな極を打ち消します。

L = G*Ka;
Ls = sample(L,[],pval);

bode(Ls)
grid on;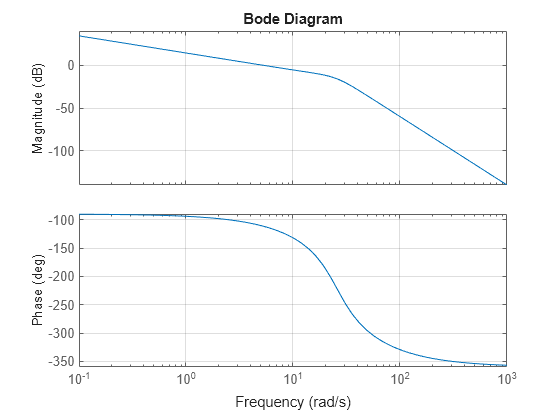

MATLAB figure

固定パラメーター値に対するステップ応答は、定常偏差ゼロ、オーバーシュートなし、整定時間 1 秒未満になります。

Ts = feedback(Ls,1);
step(Ts)
grid on;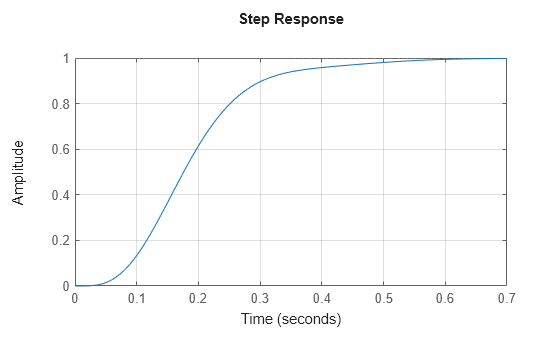

MATLAB figure

LPV の解析

feedback を使用して閉ループ LPV モデルを作成し、ゆっくり変化するパラメーター p(t) に対する LPV のステップ応答をプロットします。応答は固定の p に対する LTI の応答と同様になります。

T = feedback(L,1);

% Slow parameter variation
t = linspace(0,10,1000);
pt = cos(0.02*t);
step(T,t,pt)
title('Step response with p(t)=cos(0.02t)')
grid on

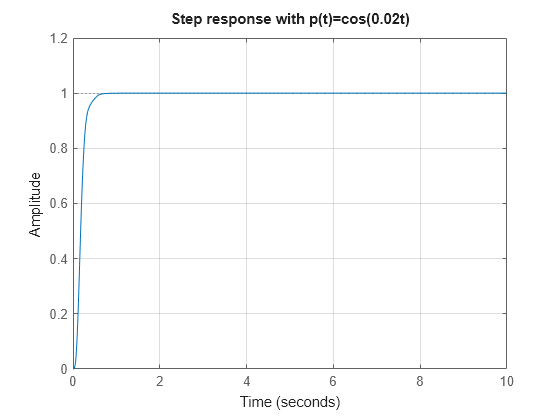
MATLAB figure

次に、変化が速いパラメーター p(t)=cos(2t) について考えます。今度はステップ応答が不安定になります。

% Fast parameter variation
t = linspace(0,100,1000);
pt = cos(2*t);
step(T,t,pt);
title('Step response with p(t)=cos(2t)')
grid on

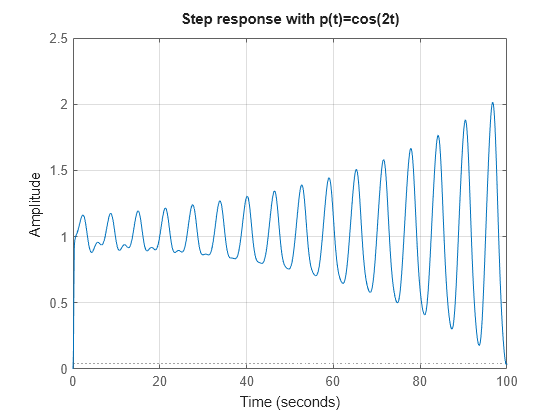
MATLAB figure

このプロットは、[1] の図 2 に対応します。ここでの不安定性は、固定パラメーターが実際のダイナミクスを反映していないことが原因です。詳細については、[1] の「Potential Hazards of Gain Scheduling」を参照してください。

プラントとコントローラーのデータ関数

type GFCN
function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = GFCN(~,p) 

% Clip p to range [-1,1]
p = max(-1,min(p,1));

A = [0 1; -1-p/2 -0.2];
B = [0; 1];
C = [1 0];
D = 0;
E = [];
dx0 = [];
x0 = [];
u0 = [];
y0 = [];
Delays = [];

type KFCN
function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = KFCN(t,p,Gaug) 
% This code solves Riccati equations and forms the gains for each value 
% of p.  This is not particularly efficient especially if used for
% simulations or real-time implementation. An alternative would be to 
% pre-solve either the Riccati equations (or the gains) on a grid of 
% parameters and then interpolate.

% Sample augmented plant to get dynamics at (t,p)
[Aaug,Baug,Caug,~] = ssdata(sample(Gaug,t,p));

% Design Parameters
N = [1; 0; 1+p/2];
mu = 0.01;
rho = 1e-8;

% Solve observer and state-feedback Riccati equations
% The observer and state-feedback gains are given by:
%   H = Sigma*(Caug)'/mu and G = (Baug)'*Z/rho;
[~,Ht] = icare(Aaug',Caug',N*N',mu);
H = Ht';
[~,G] = icare(Aaug,Baug,Caug'*Caug,rho);

% Observer / state-feedback with integral action (See Fig. 1 of [1]).
K = ss(Aaug-Baug*G-H*Caug, -H,-G,0);
Ka = tf(1,[1 0])*K;
[Ak,Bk,Ck,Dk] = ssdata(Ka);

% State-space and offset data: 
A = Ak;
B = Bk;
C = Ck;
D = Dk;
E = [];
dx0 = [];
x0 = [];
u0 = [];
y0 = [];
Delays = [];

参考文献

[1] Shamma, J. S., and M. Athans. “Gain Scheduling: Potential Hazards and Possible Remedies.” IEEE Control Systems 12, no. 3 (June 1992): 101–7. https://doi.org/10.1109/37.165527.

[2] Shamma, "Analysis and Design of Gain Scheduled Control Systems," Ph.D. Thesis, MIT, 1988.

参考

|

トピック