このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
comm.DecisionFeedbackEqualizer
判定フィードバック フィルター処理を使用した変調信号のイコライズ
説明
comm.DecisionFeedbackEqualizer System object™ は、重み付き和をもつ判定フィードバック フィルター タップ付き遅延線を使用して、分散チャネルを介して送信される変調信号をイコライズします。イコライザー オブジェクトは、選択されたアルゴリズムに基づいてタップ重みを適応的に調整します。詳細については、アルゴリズムを参照してください。
判定フィードバック フィルターを使用して変調信号をイコライズするには:
comm.DecisionFeedbackEqualizerオブジェクトを作成し、そのプロパティを設定します。関数と同様に、引数を指定してオブジェクトを呼び出します。
System object の機能の詳細については、System object とはを参照してください。
作成
説明
dfe = comm.DecisionFeedbackEqualizer
dfe = comm.DecisionFeedbackEqualizer(Name,Value)comm.DecisionFeedbackEqualizer('Algorithm','RLS') は、再帰的最小二乗 (RLS) アルゴリズムを使用してタップ重みを更新するようにイコライザー オブジェクトを構成します。各プロパティ名を引用符で囲みます。
プロパティ
使用法
構文
説明
y = dfe(x,aw)aw も指定します。aw が true の場合、System object はイコライザーのタップ重みを適応させます。aw が false の場合、System object は重みを変更せずに維持します。この構文を有効にするには、Algorithm プロパティを 'CMA' に設定し、AdaptWeightsSource プロパティを 'Input port' に設定します。
入力引数
出力引数
オブジェクト関数
オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステム リソースを解放するには、次の構文を使用します。
release(obj)
例
BPSK 変調信号の判定フィードバック イコライズ
8 つのフォワード タップと 5 つのフィードバック タップをもち、ステップ サイズが 0.03 の判定フィードバック LMS イコライザーを指定して、BPSK 変調器とイコライザー System object™ を作成します。
bpsk = comm.BPSKModulator; eqdfe_lms = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',8,'NumFeedbackTaps',5,'StepSize',0.03);
イコライザーのリファレンス タップ インデックスを変更します。
eqdfe_lms.ReferenceTap = 4;
テスト データのセットを作成します。信号の畳み込みを行ってデータを受信します。
x = bpsk(randi([0 1],1000,1)); rxsig = conv(x,[1 0.8 0.3]);
maxstep を使用して最大許容ステップ サイズを求めます。
mxStep = maxstep(eqdfe_lms,rxsig)
mxStep = 0.1028
受信信号をイコライズします。最初の 200 個のシンボルをトレーニング シーケンスとして使用します。
y = eqdfe_lms(rxsig,x(1:200));
QPSK 変調信号の判定フィードバック イコライズ
最小平均二乗 (LMS) アルゴリズムを使用した判定フィードバック イコライズを適用して、遅延したマルチパス AWGN チャネル経由で渡した QPSK シンボルを復元します。
シミュレーション変数を初期化します。
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
chtaps = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];QPSK 変調されたシンボルを生成します。シンボルに遅延したマルチパス チャネルのフィルター処理と AWGN 障害を適用します。
data = randi([0 M-1], numSymbols, 1);
tx = pskmod(data, M, pi/4);
rx = awgn(filter(chtaps,1,tx),25,'measured');判定フィードバック イコライザー System object を作成し、既定の構成を表示します。リファレンス タップを 1 に調整します。最大許容ステップ サイズをチェックします。劣化したシンボルをイコライズします。
eq = comm.DecisionFeedbackEqualizer
eq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 5
NumFeedbackTaps: 3
StepSize: 0.0100
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
eq.ReferenceTap = 1; mxStep = maxstep(eq,rx)
mxStep = 0.2149
[y,err,weights] = eq(rx,tx(1:numTrainingSymbols));
劣化したシンボルとイコライズされたシンボルのコンスタレーションをプロットします。
constell = comm.ConstellationDiagram('NumInputPorts',2);
constell(rx,y)
イコライザーの誤差信号をプロットし、イコライズされたシンボルのエラー ベクトル振幅を計算します。
plot(abs(err)) grid on; xlabel('Symbols'); ylabel('|e|')
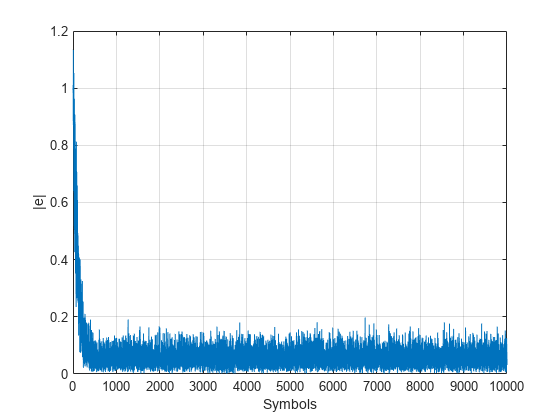
errevm = comm.EVM; evm = errevm(tx,y)
evm = 10.1268
イコライザーのタップ重みをプロットします。
subplot(3,1,1); stem(real(weights)); ylabel('real(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], ... [-0.5 1],'Color','r','LineWidth',1) title('Equalizer Tap Weights') subplot(3,1,2); stem(imag(weights)); ylabel('imag(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], ... [-0.5 1],'Color','r','LineWidth',1) subplot(3,1,3); stem(abs(weights)); ylabel('abs(weights)'); xlabel('Tap'); grid on; axis([1 8 -0.5 1]) line([eq.NumForwardTaps+0.5 eq.NumForwardTaps+0.5], ... [-0.5 1],'Color','r','LineWidth',1)
異なる学習スキームを使用した判定フィードバック イコライズ システム
最小平均二乗 (LMS) アルゴリズムを使用した判定フィードバック イコライズを示し、AWGN チャネル経由で渡した QPSK シンボルを復元します。異なるイコライザーの学習スキームを適用して、シンボルの誤差の大きさを示します。
システム設定
AWGN の影響を受ける QPSK 変調システムをシミュレートします。200 個のトレーニング シンボルと 1800 個のランダム データ シンボルで構成されるパケットを送信します。パケット データを復元するように判定フィードバック LMS イコライザーを構成します。
M = 4; numTrainSymbols = 200; numDataSymbols = 1800; SNR = 20; trainingSymbols = ... pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4); numPkts = 10; dfeq = comm.DecisionFeedbackEqualizer( ... Algorithm="LMS", ... NumForwardTaps=5, ... NumFeedbackTaps=4, ... ReferenceTap=3, ... StepSize=0.01);
リセットを使用する各パケットの先頭でのイコライザーの学習
先頭に追加されたトレーニング シンボルを使用して各パケットを処理します。各パケットの処理後にイコライザーをリセットします。各パケットの後にイコライザーをリセットすると、イコライザーは事前知識なしにタップを学習するようになります。最初、2 番目、および最後のパケットのイコライザー誤差信号プロットは、各パケットの先頭でシンボル誤りが多くなっていることを示しています。
jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; rx = awgn(packet,SNR); [~,err] = dfeq(rx,trainingSymbols); reset(dfeq) if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) ylim([0 1]) title(['Packet # ',num2str(ii)]) xlabel('Symbols'); ylabel('Error Magnitude'); grid on; jj = jj+1; end end
リセットを使用しない各パケットの先頭でのイコライザーの学習
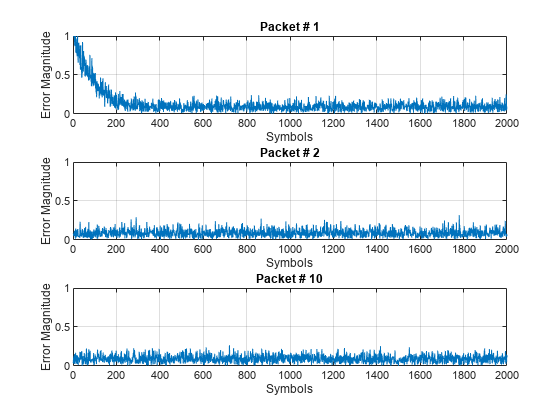
先頭に追加されたトレーニング シンボルを使用して各パケットを処理します。各パケットの処理後にイコライザーをリセットしません。各パケットの後にリセットしないことで、イコライザーは前のパケットの学習によるタップ重みを保持します。最初、2 番目、および最後のパケットのイコライザー誤差信号プロットは、最初のパケットに対する初期学習の後に、後続のパケットが各パケットの先頭でシンボル誤りが少なくなることを示しています。
release(dfeq) jj = 1; figure for ii = 1:numPkts b = randi([0 M-1],numDataSymbols,1); dataSym = pskmod(b,M,pi/4); packet = [trainingSymbols;dataSym]; channel = 1; rx = awgn(packet*channel,SNR); [~,err] = dfeq(rx,trainingSymbols); if (ii ==1 || ii == 2 ||ii == numPkts) subplot(3,1,jj) plot(abs(err)) ylim([0 1]) title(['Packet # ',num2str(ii)]) xlabel('Symbols'); ylabel('Error Magnitude'); grid on; jj = jj+1; end end
周期的なイコライザーの学習
時変チャネルの影響を受ける信号があるシステムには、チャネル変動に対してロックを維持するために周期的なイコライザーの学習が必要です。1800 個のデータ シンボルごとに 200 個のシンボルの学習を行うシステムを指定します。学習の合間では、イコライザーはタップ重みを更新しません。イコライザーはパケットあたり 200 個のシンボルを処理します。
Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);AdaptAfterTraining プロパティを false に設定して、学習フェーズの後にイコライザーのタップ重みの更新を停止します。
release(dfeq) dfeq.AdaptAfterTraining = false
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 5
NumFeedbackTaps: 4
StepSize: 0.0100
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 3
InputDelay: 0
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: false
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
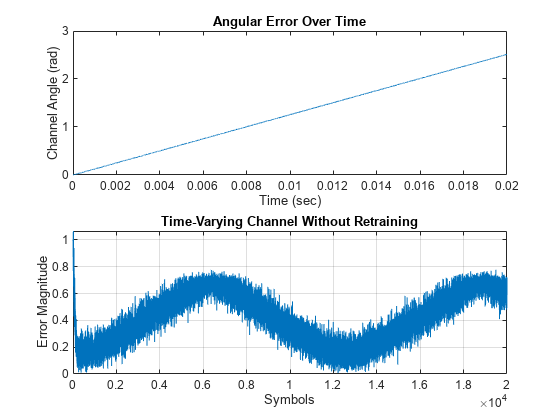
劣化したデータをイコライズします。チャネルからの角度誤差、イコライザーの誤差信号、および信号コンスタレーションをプロットします。チャネルが変動しても、イコライザー出力からチャネルの影響は除去されません。また、出力コンスタレーションが同期せずに回転し、ビット誤りが発生します。
[y,err] = dfeq(rx,trainingSymbols); figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('Time (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(err)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel Without Retraining')
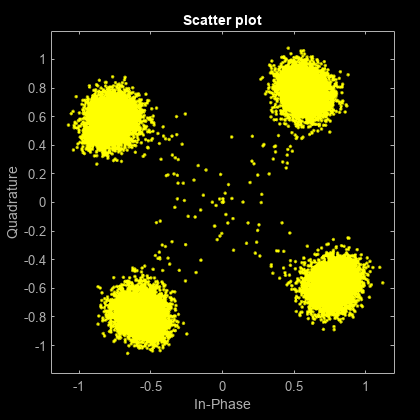
scatterplot(y)
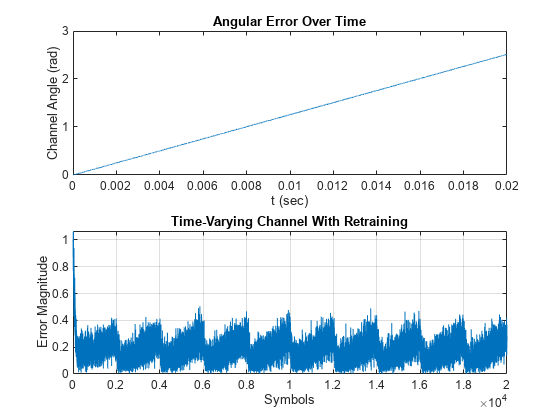
TrainingInputPort プロパティを true に設定し、trainFlag 入力により信号が送られたときにタップを再学習するようにイコライザーを構成します。イコライザーは、trainFlag が true の場合にのみ学習を行います。イコライザーは 2000 個のシンボルごとにタップを再学習し、チャネルの変動に対してロックを維持します。チャネルからの角度誤差、イコライザーの誤差信号、および信号コンスタレーションをプロットします。チャネルが変動すると、イコライザー出力からチャネルの影響が除去されます。また、出力コンスタレーションが同期せずに回転することがなくなり、ビット誤りが減少します。
release(dfeq) dfeq.TrainingFlagInputPort = true; symbolCnt = 0; numPackets = length(rx)/spp; trainFlag = true; trainingPeriod = 2000; eVec = zeros(size(rx)); yVec = zeros(size(rx)); for p=1:numPackets [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ... dfeq(rx((p-1)*spp+1:p*spp,1), ... trainingSymbols,trainFlag); symbolCnt = symbolCnt + spp; if symbolCnt >= trainingPeriod trainFlag = true; symbolCnt = 0; else trainFlag = false; end end figure subplot(2,1,1) plot(tx, unwrap(angle(channel))) xlabel('t (sec)') ylabel('Channel Angle (rad)') title('Angular Error Over Time') subplot(2,1,2) plot(abs(eVec)) xlabel('Symbols') ylabel('Error Magnitude') grid on title('Time-Varying Channel With Retraining')
scatterplot(yVec)
遅延信号の判定フィードバック イコライズ
送信シンボルと受信サンプルの間に遅延があるシステムをシミュレートします。一般的なシステムには送信側と受信側のフィルターがあり、これにより遅延が発生します。システムを同期させるには、この遅延を考慮しなければなりません。この例では、送信フィルターと受信フィルターを使用せずにシステム遅延が発生しています。判定フィードバック イコライズは、最小平均二乗 (LMS) アルゴリズムを使用して、QPSK シンボルを復元します。
シミュレーション変数を初期化します。
M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;QPSK 変調されたシンボルを生成します。送信シンボルにマルチパス チャネルのフィルター処理、システム遅延、および AWGN を適用します。
data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); % OQPSK delayedSym = systemDelay(filter(mpChan,1,tx)); rx = awgn(delayedSym,snr,'measured');
イコライザーおよび EVM の System object を作成します。イコライザー System object は、LMS アルゴリズムを使用して判定フィードバック イコライザーを指定します。
dfeq = comm.DecisionFeedbackEqualizer('Algorithm','LMS', ... 'NumForwardTaps',9,'NumFeedbackTaps',6,'ReferenceTap',5); evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation');
入力遅延を調整しないイコライズ
受信シンボルをイコライズします。
[y1,err1,wts1] = dfeq(rx,tx(1:numTrainingSymbols,1));
関数 finddelay を使用して、受信シンボルと送信シンボルの間の遅延を検出します。
rxDelay = finddelay(tx,rx)
rxDelay = 20
イコライザー情報を表示します。レイテンシ値は、イコライザーによって発生した遅延を示します。合計遅延を、rxDelay とイコライザーのレイテンシの合計として計算します。
eqInfo = info(dfeq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency;
イコライザー出力が収束するまで、シンボル エラー レートは高くなります。誤り出力 err1 をプロットして、イコライズされた出力がいつ収束するかを判断します。
plot(abs(err1)) xlabel('Symbols') ylabel('Error Magnitude') title('Equalizer Error Signal')
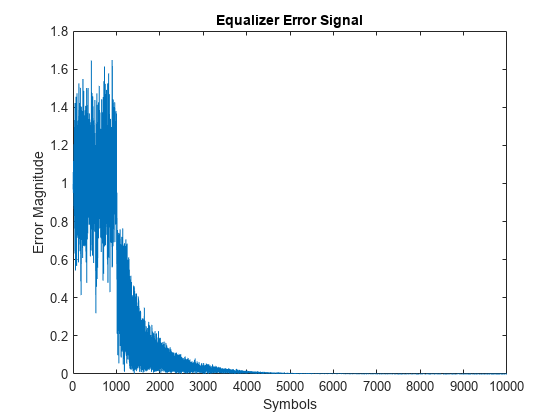
このプロットでは、最初の 2000 個のシンボルの過度な誤りが示されています。シンボルを復調してシンボル誤りを計算するときは、収束していない出力と、イコライザー出力と送信シンボルの間のシステム遅延を考慮します。
dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4); symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 5977
evmWithDelay = evm(y1)
evmWithDelay = 26.3382
イコライザー System object で受信遅延が考慮されていないため、エラー レートと EVM が高くなります。
判定フィードバック イコライザーの入力遅延の調整
遅延値を使用して InputDelay プロパティを設定し、受信データをイコライズします。InputDelay は調整できないプロパティであるため、InputDelay プロパティを再構成するには dfeq System object を解放しなければなりません。受信シンボルをイコライズします。
release(dfeq) dfeq.InputDelay = rxDelay
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'LMS'
NumForwardTaps: 9
NumFeedbackTaps: 6
StepSize: 0.0100
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 5
InputDelay: 20
InputSamplesPerSymbol: 1
TrainingFlagInputPort: false
AdaptAfterTraining: true
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
[y2,err2,wts2] = dfeq(rx,tx(1:numTrainingSymbols,1));
タップ重みとイコライズされた誤差の大きさをプロットします。ステム プロットは、システム遅延が除去される前後のイコライザーのタップ重みを示します。2 次元ライン プロットは、遅延が除去された信号と比較して、遅延信号のイコライザー収束が遅いことを示しています。
subplot(2,1,1) stem([real(wts1),real(wts2)]) xlabel('Taps') ylabel('Tap Weight Real') legend('rxDelayed','rxDelayRemoved') grid on subplot(2,1,2) stem([imag(wts1),imag(wts2)]) xlabel('Taps') ylabel('Tap Weight Imaginary') legend('rxDelayed','rxDelayRemoved') grid on
figure plot([abs(err1),abs(err2)]) xlabel('Symbols') ylabel('Error Magnitude') legend('rxDelayed','rxDelayRemoved') grid on
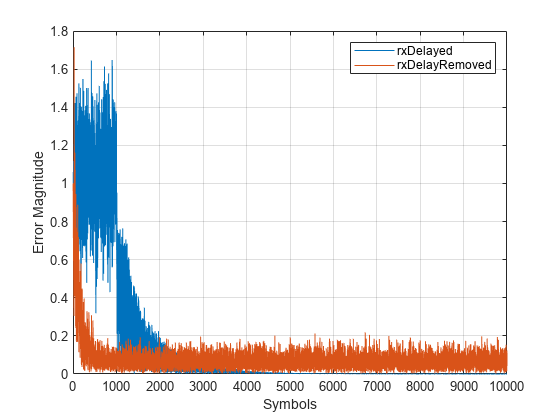
イコライズされた信号 rxDelayed および rxDelayRemoved の誤り出力をプロットします。遅延が除去された信号では、イコライザーは 1000 個のシンボルの学習期間中に収束します。シンボルを復調してシンボル誤りを計算するときは、収束していない出力と、イコライザー出力と送信シンボルの間のシステム遅延を考慮して、最初の 500 個のシンボルをスキップします。システム遅延を考慮するためにイコライザーを再構成すると、信号のイコライズが改善され、シンボル誤りと EVM が減少します。
eqInfo = info(dfeq)
eqInfo = struct with fields:
Latency: 4
totalDelay = rxDelay + eqInfo.Latency; dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4); symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0
evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 7.5357
EVM ベースの学習を使用したシンボルの判定フィードバック イコライズ
定包絡線基準アルゴリズム (CMA) と EVM ベースのタップの学習を使用して、判定イコライザーで QPSK シンボルを復元します。CMA などのブラインド イコライザー アルゴリズムを使用する場合は、AdaptWeights プロパティを使用して学習を開始および停止し、イコライザーのタップを学習することができます。補助関数を使用してプロットを生成し、位相補正を適用します。
システム変数を初期化します。
rng(123456); M = 4; % QPSK numSymbols = 100; numPackets = 5000; refTap = 3; nFwdTaps = 5; nFdbkTaps = 4; ttlTaps = nFwdTaps + nFdbkTaps; raylChan = comm.RayleighChannel( ... 'PathDelays',[0 1], ... 'AveragePathGains',[0 -12], ... 'MaximumDopplerShift',1e-5); SNR = 50; adaptWeights = true;
イコライザーおよび EVM の System object を作成します。イコライザー System object は、CMA 適応アルゴリズムを使用して判定フィードバック イコライザーを指定します。補助関数を呼び出して Figure のプロットを初期化します。
dfeq = comm.DecisionFeedbackEqualizer( ... 'Algorithm','CMA', ... 'NumForwardTaps',nFwdTaps, ... 'NumFeedbackTaps',nFdbkTaps, ... 'ReferenceTap',refTap, ... 'StepSize',0.03, ... 'AdaptWeightsSource','Input port')
dfeq =
comm.DecisionFeedbackEqualizer with properties:
Algorithm: 'CMA'
NumForwardTaps: 5
NumFeedbackTaps: 4
StepSize: 0.0300
Constellation: [0.7071 + 0.7071i -0.7071 + 0.7071i -0.7071 - 0.7071i 0.7071 - 0.7071i]
ReferenceTap: 3
InputSamplesPerSymbol: 1
AdaptWeightsSource: 'Input port'
InitialWeightsSource: 'Auto'
WeightUpdatePeriod: 1
info(dfeq)
ans = struct with fields:
Latency: 2
evm = comm.EVM('ReferenceSignalSource', ... 'Estimated from reference constellation'); [errPlot,evmPlot,scatSym,adaptState] = ... initFigures(numPackets,ttlTaps);
イコライズ ループ
イコライズ ループを実装するには、次の手順に従います。
OQPSK データ パケットを生成します。
レイリー フェージングと AWGN を送信データに適用します。
受信データにイコライズを、イコライザー出力に位相補正を適用します。
EVM を推定し、EVM レベルに基づいて
adaptWeightsフラグをtrueまたはfalseに切り替えます。Figure のプロットを更新します。
for p=1:numPackets data = randi([0 M-1],numSymbols,1); tx = pskmod(data,M,pi/4); rx = awgn(raylChan(tx),SNR); rxDelay = finddelay(rx,tx); [y,err,wts] = dfeq(rx,adaptWeights); y = phaseCorrection(y); evmEst = evm(y); adaptWeights = (evmEst > 20); updateFigures(errPlot,evmPlot,scatSym,adaptState, ... wts,y(end),evmEst,adaptWeights,p,numPackets) end
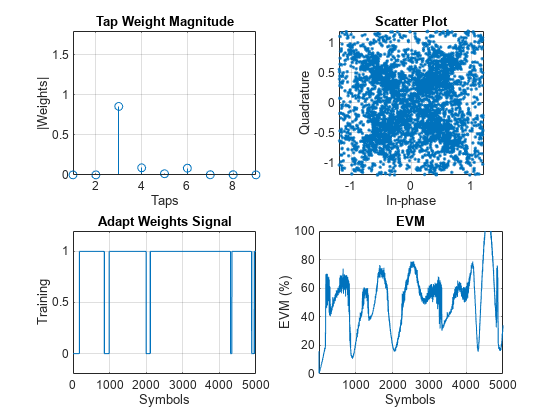
rxDelay
rxDelay = 0
Figure のプロットは、EVM が変化するにつれて、イコライザーが判定指向の重み適応モードのオンとオフを切り替えていることを示しています。
補助関数
この補助関数は、シミュレーション結果の 4 つのプロットを示す Figure を初期化します。
function [errPlot,evmPlot,scatter,adaptState] = ... initFigures(numPkts,ttlTaps) yVec = nan(numPkts,1); evmVec = nan(numPkts,1); wVec = zeros(ttlTaps,1); adaptVec = nan(numPkts,1); figure subplot(2,2,1) evmPlot = stem(wVec); grid on; axis([1 ttlTaps 0 1.8]) xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2) scatter = plot(yVec, '.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on; xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot'); subplot(2,2,3) adaptState = plot(adaptVec); grid on; axis([0 numPkts -0.2 1.2]) ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal') subplot(2,2,4) errPlot = plot(evmVec); grid on; axis([1 numPkts 0 100]) xlabel('Symbols'); ylabel('EVM (%)'); title('EVM') end
この補助関数は Figure を更新します。
function updateFigures(errPlot,evmPlot,scatSym, ... adaptState,w,y,evmEst,adaptWts,p,numFrames) persistent yVec evmVec adaptVec if p == 1 yVec = nan(numFrames,1); evmVec = nan(numFrames,1); adaptVec = nan(numFrames,1); end yVec(p) = y; evmVec(p) = evmEst; adaptVec(p) = adaptWts; errPlot.YData = abs(evmVec); evmPlot.YData = abs(w); scatSym.XData = real(yVec); scatSym.YData = imag(yVec); adaptState.YData = adaptVec; drawnow limitrate end
この補助関数は位相補正を適用します。
function y = phaseCorrection(y) a = angle(y((real(y) > 0) & (imag(y) > 0))); a(a < 0.1) = a(a < 0.1) + pi/2; theta = mean(a) - pi/4; y = y * exp(-1i*theta); end
フェージング環境でのパケット化された信号の判定フィードバック イコライズ
最小平均二乗 (LMS) アルゴリズムを使用して、判定フィードバック イコライザーでフェージング環境の QPSK シンボルを復元します。オブジェクト関数 reset を使用して、独立したパケットをイコライズします。補助関数を使用してプロットを生成します。この例では、シンボルベースの処理とフレームベースの処理も示します。
設定
システム変数を初期化し、イコライザー System object を作成して、プロット図を初期化します。
M = 4; % QPSK numSym = 1000; numTrainingSym = 100; numPackets = 5; refTap = 5; nFwdTaps = 9; nFdbkTaps = 4; ttlTaps = nFwdTaps + nFdbkTaps; stepsz = 0.01; ttlNumSym = numSym + numTrainingSym; raylChan = comm.RayleighChannel( ... 'PathDelays',[0 1], ... 'AveragePathGains',[0 -9], ... 'MaximumDopplerShift',0, ... 'PathGainsOutputPort',true); SNR = 35; rxVec = zeros(ttlNumSym,numPackets); txVec = zeros(ttlNumSym,numPackets); yVec = zeros(ttlNumSym,1); eVec = zeros(ttlNumSym,1); dfeq1 = comm.DecisionFeedbackEqualizer( ... 'Algorithm','LMS', ... 'NumForwardTaps',nFwdTaps, ... 'NumFeedbackTaps',nFdbkTaps, ... 'ReferenceTap',refTap, ... 'StepSize',stepsz, ... 'TrainingFlagInputPort',true); [errPlot,wStem,hStem,scatPlot] = ... initFigures(ttlNumSym,ttlTaps, ... raylChan.AveragePathGains);
シンボルベースの処理
シンボルベースの処理では、イコライザーの入力で 1 つのシンボルを指定します。各パケットの処理後にイコライザーの状態とチャネルをリセットします。
for p = 1:numPackets trainingFlag = true; for q=1:ttlNumSym data = randi([0 M-1],1,1); tx = pskmod(data,M,pi/4); [xc,pg] = raylChan(tx); rx = awgn(xc,25); [y,err,wts] = dfeq1(rx,tx,trainingFlag);
numTrainingSym 個のトレーニング シンボルを処理した後に学習を無効にします。
if q == numTrainingSym trainingFlag = false; end updateFigures(errPlot,wStem,hStem, ... scatPlot,err,wts,y,pg,q,ttlNumSym); txVec(q,p) = tx; rxVec(q,p) = rx; end
各パケットの処理後に、チャネル System object をリセットしてチャネル タップの新しい実現を取得し、イコライザー System object をリセットして既定のタップ重みに戻します。
reset(raylChan)
reset(dfeq1)
end
パケットベースの処理
パケットベースの処理では、イコライザーの入力で 1 つのパケットを指定します。各パケットには ttlNumSym 個のシンボルが含まれています。学習期間がパケット長よりも短いため、学習の開始の入力を指定する必要はありません。
yVecPkt = zeros(ttlNumSym,numPackets); errVecPkt = zeros(ttlNumSym,numPackets); wgtVecPkt = zeros(ttlTaps,numPackets); dfeq2 = comm.DecisionFeedbackEqualizer( ... 'Algorithm','LMS', ... 'NumForwardTaps',nFwdTaps, ... 'NumFeedbackTaps',nFdbkTaps, ... 'ReferenceTap',refTap, ... 'StepSize',stepsz); for p = 1:numPackets [yVecPkt(:,p),errVecPkt(:,p),wgtVecPkt(:,p)] = ... dfeq2(rxVec(:,p),txVec(1:numTrainingSym,p)); for q=1:ttlNumSym updateFigures(errPlot,wStem,hStem,scatPlot, ... errVecPkt(q,p),wgtVecPkt(:,p),yVecPkt(q,p), ... pg,q,ttlNumSym); end
各パケットの処理後に、チャネル System object をリセットしてチャネル タップの新しい実現を取得し、イコライザー System object をリセットして既定のタップ重みに戻します。
reset(raylChan)
reset(dfeq2)
end
補助関数
この補助関数は Figure を初期化します。
function [errPlot,wStem,hStem,scatPlot] = ... initFigures(ttlNumSym,ttlTap,pg) yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); wVec = zeros(ttlTap,1); figure; subplot(2,2,1); wStem = stem(wVec); axis([1 ttlTap 0 1.8]); grid on; xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude') subplot(2,2,2); hStem = stem([0 abs(pg) 0]); grid on; xlabel('Taps'); ylabel('|Path Gain|'); title('Channel Path Gain Magnitude') subplot(2,2,3); errPlot = plot(eVec); axis([1 ttlNumSym 0 1.2]); grid on xlabel('Symbols'); ylabel('|Error Magnitude|'); title('Error Magnitude') subplot(2,2,4); scatPlot = plot(yVec,'.'); axis square; axis([-1.2 1.2 -1.2 1.2]); grid on; xlabel('In-phase'); ylabel('Quadrature'); title(sprintf('Scatter Plot')); end
この補助関数は Figure を更新します。
function updateFigures(errPlot,wStem,hStem,scatPlot, ... err,wts,y,pg,p,ttlNumSym) persistent yVec eVec if p == 1 yVec = nan(ttlNumSym,1); eVec = nan(ttlNumSym,1); end yVec(p) = y; eVec(p) = abs(err); errPlot.YData = abs(eVec); wStem.YData = abs(wts); hStem.YData = [0 abs(pg) 0]; scatPlot.XData = real(yVec); scatPlot.YData = imag(yVec); drawnow limitrate end
詳細
アルゴリズム
判定フィードバック イコライザー
判定フィードバック イコライザー (DFE) は、周波数選択性チャネルでの符号間干渉 (ISI) を軽減する非線形イコライザーです。チャネルの周波数応答に null が存在する場合、DFE はノイズを強調しません。DFE は、入力信号からのサンプルを格納し、フォワード フィルターとフィードバック フィルターを含む、タップ付き遅延線で構成されます。フォワード フィルターは、線形イコライザーに類似しています。フィードバック フィルターは、入力がイコライズされた信号に行われる判定であるようなタップ付き遅延線を含みます。シンボル周期ごとに一度、イコライザーは遅延ラインで値の重み付き総和を出力し、次のシンボル周期のための準備として重みを更新します。
DFE はシンボル間隔または分数シンボル間隔にすることができます。
シンボル間隔イコライザーの場合、シンボルあたりのサンプル数 K は 1 です。出力サンプル レートは入力サンプル レートと等しくなります。
分数シンボル間隔イコライザーの場合、シンボルあたりのサンプル数 K は 1 より大きい整数です。通常、分数シンボル間隔イコライザーの K は 4 です。出力サンプルレートは 1/T、入力サンプルレートは K/T になります。タップ重みの更新は、出力レートで起こります。
この図は、合計 N 個の重みをもち、シンボル周期が T で、シンボルあたりのサンプル数が K 個の分数シンボル間隔 DFE を示しています。フィルターには、L 個のフォワードの重みと N-L 個のフィードバックの重みがあります。フォワード フィルターは最上部にあり、フィードバック フィルターは最下部にあります。K が 1 の場合、結果は分数シンボル間隔 DFE ではなくシンボル間隔 DFE です。
各シンボル周期において、イコライザーは、フォワード フィルターで K 個の入力サンプルを受信し、フィードバック フィルターで 1 つの判定またはトレーニング サンプルを受信します。それから、イコライザーは、フォワードおよびフィードバック遅延線に、値の重み付き総和を出力し、重みを更新して次のシンボル周期に備えます。
メモ
図の Adaptive Algorithm ブロックに対するアルゴリズムは、フォワードおよびフィードバックの重みを同時に最適化します。同時最適化は、再帰的最小二乗 (RLS) アルゴリズムの収束のために特に重要です。
詳細については、イコライズを参照してください。
拡張機能
バージョン履歴
R2019a で導入
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)