イコライズ
マルチパス フェージング散乱環境において、受信機では通常、複数の絶えず変化する送信信号の遅延が検出されます。これらの時分散チャネルは、符号間干渉 (ISI) の原因となります。これは、複数のパスから受信したシンボルが遅延して時間的にオーバーラップしたときに発生します。複数の受信パスからのシンボルが互いに干渉し、受信機で区別できなくなるため、ISI は高いエラー レートの原因となります。
イコライザーは、ISI の軽減および受信機のパフォーマンス向上を試みます。イコライザー構造は、伝播チャネルの応答の一致を試みるフィルターです。時変伝播チャネルの場合は、イコライズ フィルターのタップ重みを適応させて、時間の経過に沿ってチャネルとの一致を維持することで、エラー レート性能が向上します。
イコライザー構造のオプション
Communications Toolbox™ には、線形、判定フィードバック、または最尤系列推定 (MLSE) のイコライズ構造を使用して送信データを復元するための System object とブロックが用意されています。詳細については、イコライザーについての参考文献を参照してください。
この図は、各イコライズ構造の大まかな構成オプションを示しています。
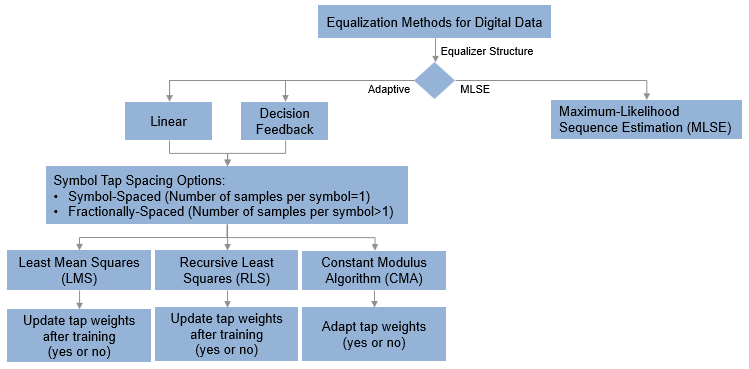
各イコライザー構造で、構造設定 (タップ数やタップ重みの初期セットなど)、アルゴリズム設定 (ステップ サイズなど)、および設計内の変調器で使用される信号コンスタレーションを構成できます。また、シミュレーション全体を通じたイコライザーのタップ重みの適応性も指定します。
線形フィルターおよび判定フィードバック フィルターのイコライザー構造は、LMS、RLS、または CMA 適応アルゴリズムを使用してタップ重みを適応させます。これらのイコライザー構造を使用する場合は、シンボルあたりのサンプル数によって、シンボルの処理に整数のシンボル間隔が使用されるか、非整数のシンボル間隔が使用されるかが決まります。
LMS および RLS 適応アルゴリズムを使用する場合、イコライザーはタップ重みトレーニング モードで動作を開始します。イコライザーを構成して、判定指向モードで適応的に動作させるか、学習の完了後にタップをさらに調整せずに動作させます。
CMA 適応アルゴリズムを使用する場合、イコライザーにトレーニング モードはありません。イコライザーを構成して、判定指向モードで適応的に動作させるか、非適応モードで動作させることができます。
線形フィルターおよび判定フィードバック フィルターのイコライザーの機能については、適応イコライザーを参照してください。
最尤系列推定 (MLSE) イコライザーは、ビタビ アルゴリズムを使用します。MLSE イコライズ構造は受信シンボルに対する最適な一致を提供しますが、正確なチャネル推定が必要となり、最も計算が複雑な構造です。MLSE イコライザーの機能の詳細については、MLSE イコライザーを参照してください。
各イコライズ構造の計算量は、チャネルの時間分散の長さと共に増大します。チャネルのドップラー特性と周波数選択性特性を考慮して、シミュレーションで使用するイコライズ構造を選択するときにこの表の情報を使用してください。
| イコライザー構造体 | ドップラー速度 | チャネル周波数の選択 | 計算量 |
|---|---|---|---|
| ライン RLS | 高 | なし | 中 |
| ライン LMS | 低 | なし | 最小 |
| ライン CMA | 低 | なし | 最小 |
| DFE RLS | 高 | あり | 中 |
| DFE LMS | 低 | あり | 最小 |
| DFE CMA | 低 | あり | 最小 |
| MLSE | 低 | あり | 最大 |
イコライザーについての参考文献
[1] Farhang-Boroujeny, B., Adaptive Filters: Theory and Applications, Chichester, England, John Wiley & Sons, 1998.
[2] Haykin, Simon, Adaptive Filter Theory, Third Ed., Upper Saddle River, NJ, Prentice-Hall, 1996.
[3] Kurzweil, Jack, An Introduction to Digital Communications, New York, John Wiley & Sons, 2000.
[4] Proakis, John G., Digital Communications, Fourth Ed., New York, McGraw-Hill, 2001.
[5] Steele, Raymond, Ed., Mobile Radio Communications, Chichester, England, John Wiley & Sons, 1996.