MATLAB を使用した 16-QAM の調査

ステップ 3 - 1: MATLAB を使用した AWGN がある QAM システムの BER の計算

この例では、ベースバンド変調器、チャネル、復調器で構成される通信リンクを使用してデータストリームを処理する方法を示します。この例では、ランダムデータの一部をステムプロットで表示し、送信信号と受信信号をコンスタレーションダイアグラムで表示し、ビットエラーレート (BER) を計算します。この通信リンクにパルス整形フィルターを追加するには、16-QAM 信号でのパルス整形の使用の例を参照してください。パルス整形フィルターを適用した通信リンクに前方誤り訂正を追加するには、16-QAM 信号での前方誤り訂正の使用の例を参照してください。

ランダムな信号の変調

変調スキームにベースバンド 16-QAM を使用し、信号が加法性ホワイトガウスノイズ (AWGN) チャネルを通過するようにします。基本のシミュレーション操作として、Communications Toolbox™ および MATLAB® の次の関数を使用します。

rng — 乱数発生の制御
randi — ランダムデータストリームの生成
bit2int — バイナリデータから整数値のシンボルへの変換
qammod — 16-QAM を使用した変調
comm.AWGNChannel — AWGN を使用した送信データの劣化
scatterplot — コンスタレーションダイアグラムの作成
qamdemod — 16-QAM を使用した復調
int2bit — 整数値のシンボルからバイナリデータへの変換
biterr — システムの BER の計算

ランダムなバイナリデータフレームの生成

MATLAB で信号を表すための通常の形式は、ベクトルまたは行列です。データストリームの長さ (すなわち、列ベクトル内の行数) は 30,000 に設定されます。例で結果を繰り返し再現できるように、関数 rng を既定の状態または静的なシード値に設定します。次に、関数 randi を使用して、バイナリデータストリームの乱数値を含む列ベクトルを生成します。

パラメーターを定義します。

M = 16;      % Modulation order
k = log2(M); % Number of bits per symbol
n = 30000;   % Number of symbols per frame
sps = 1;     % Number of samples per symbol (oversampling factor)
rng default  % Use default random number generator

dataIn = randi([0 1],n*k,1); % Generate vector of binary data

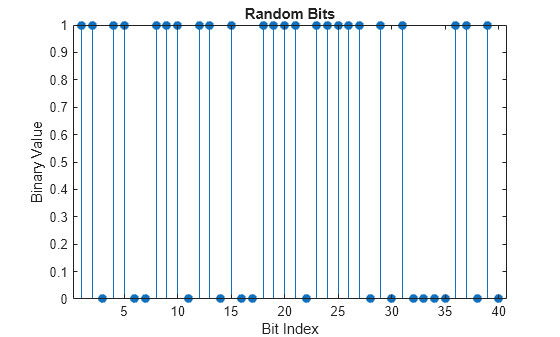
ステムプロットを使用してランダムなバイナリデータストリームの最初の 40 ビットのバイナリ値を表示します。関数 stem の呼び出しでコロン (:) 演算子を使用してバイナリベクトルの一部を選択します。

stem(dataIn(1:40),'filled');
title('Random Bits');
xlabel('Bit Index');
ylabel('Binary Value');

バイナリデータから整数値のシンボルへの変換

関数 qammod の既定の構成では、変調する入力シンボルとして整数値データが想定されています。この例では、関数 qammod を使用する前にバイナリデータストリームを前処理して整数値にします。具体的には、関数 bit2int を使用して 4 組ずつ、範囲 [0, (M–1)] 内の対応する整数に変換します。この例では、変調次数 M は 16 です。

$k = l o g_{2} (M)$ で定義されるシンボルごとのビット数を指定して、ビットからシンボルへのマッピングを実行します。その後、関数 bit2int を使用して 4 組ずつ整数値に変換します。

dataSymbolsIn = bit2int(dataIn,k);

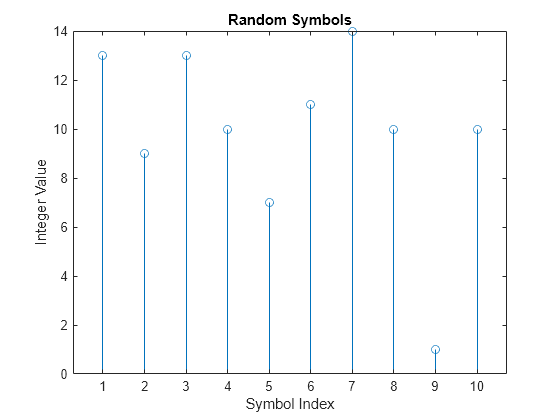
最初の 10 個のシンボルをステムプロットにプロットします。

figure;                    % Create new figure window.
stem(dataSymbolsIn(1:10));
title('Random Symbols');
xlabel('Symbol Index');
ylabel('Integer Value');

16-QAM を使用した変調

バイナリ符号化とグレイ符号化のビットをシンボルにマッピングするために、関数 qammod を使用して、位相オフセットがゼロの 16-QAM 変調を dataSymbolsIn 列ベクトルに適用します。

dataMod = qammod(dataSymbolsIn,M,'bin'); % Binary-encoded
dataModG = qammod(dataSymbolsIn,M);      % Gray-encoded

この変調処理により、16-QAM 信号コンスタレーションの要素となる値が格納された複素数列ベクトルが出力されます。この例では、この後に示すコンスタレーションダイアグラムでバイナリシンボルマッピングとグレイシンボルマッピングを表示します。

変調関数の詳細については、ベースバンドデジタル変調を参照してください。位相偏移変調 (PSK) 変調でグレイ符号化を使用する例については、シンボルマッピングの例を参照してください。

ホワイトガウスノイズの追加

変調された信号は、関数 awgn を使用して、指定された S/N 比 (SNR) でチャネルを通じて渡されます。ノイズパワースペクトル密度に対する 1 ビットあたりのエネルギーの比 ( $E_{b} / N_{0}$ ) を関数 awgn で使用する SNR 値に変換します。変数 sps は、この例では重要な役割を果たすわけではありませんが、使用するとパルス整形を使用する場合の例の拡張が簡単になります。詳細については、16-QAM 信号でのパルス整形の使用の例を参照してください。

関数convertSNRを使用して、チャネルの $E_{b} / N_{0}$ が 10 dB である場合の SNR を計算します。

EbNo = 10;
snr = convertSNR(EbNo,'ebno', ...
    samplespersymbol=sps, ...
    bitspersymbol=k);

バイナリ符号化とグレイ符号化のシンボルマッピング用に、AWGN チャネル経由で信号を渡します。

receivedSignal = awgn(dataMod,snr,'measured');
receivedSignalG = awgn(dataModG,snr,'measured');

コンスタレーションダイアグラムの作成

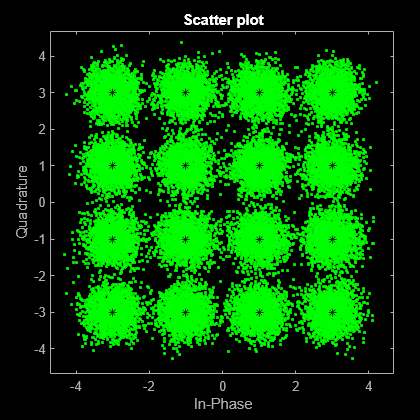
関数 scatterplot を使用して、変調した信号 dataMod とチャネルの後に受信したノイズ信号の同相成分と直交成分を表示します。AWGN の影響がコンスタレーションダイアグラムに表示されます。

sPlotFig = scatterplot(receivedSignal,1,0,'g.');
hold on
scatterplot(dataMod,1,0,'k*',sPlotFig)

16-QAM の復調

関数 qamdemod を使用して、受信データを復調し、整数値データシンボルを出力します。

dataSymbolsOut = qamdemod(receivedSignal,M,'bin'); % Binary-encoded data symbols
dataSymbolsOutG = qamdemod(receivedSignalG,M);     % Gray-coded data symbols

整数値のシンボルからバイナリデータへの変換

関数 int2bit を使用して、QAM 復調器からのバイナリ符号化されたデータシンボルを $(N_{sym} \times N_{bits / sym})$ の長さのバイナリベクトルに変換します。 $N_{sym}$ は QAM シンボルの合計数、 $N_{bits / sym}$ はシンボルごとのビット数です。16-QAM の場合は $N_{bits / sym}$ = 4 です。グレイ符号化されたシンボルに対して処理を繰り返します。

この例で前に実行したビットからシンボルへのマッピングを元に戻します。

dataOut = int2bit(dataSymbolsOut,k);
dataOutG = int2bit(dataSymbolsOutG,k);

システム BER の計算

関数 biterr を使用して、元のバイナリデータストリーム dataIn と受信したデータストリーム dataOut および dataOutG からビットエラー統計を計算します。グレイ符号化によって BER が大幅に減少しています。

エラーレート関数を使用して誤り統計を計算します。関数 fprintf を使用して結果を表示します。

[numErrors,ber] = biterr(dataIn,dataOut);
fprintf('\nThe binary coding bit error rate is %5.2e, based on %d errors.\n', ...
    ber,numErrors)

The binary coding bit error rate is 2.13e-03, based on 255 errors.

[numErrorsG,berG] = biterr(dataIn,dataOutG);
fprintf('\nThe Gray coding bit error rate is %5.2e, based on %d errors.\n', ...
    berG,numErrorsG)

The Gray coding bit error rate is 1.67e-03, based on 200 errors.

信号コンスタレーションのプロット

コンスタレーションダイアグラムには、以前に QAM コンスタレーションでプロットした点が表示されていますが、そのときはシンボル値とコンスタレーション点の間のマッピングは示していませんでした。このセクションでは、コンスタレーションダイアグラムでバイナリ符号化とグレイ符号化のデータからコンスタレーション点へのマッピングを示します。

16-QAM コンスタレーションにおける通常の符号とグレイ符号のバイナリシンボルマッピングの表示

バイナリ符号のシンボルマッピングとグレイ符号のシンボルマッピングを使用して、一連のすべてのコンスタレーション点に 16-QAM 変調を適用します。

M = 16;                       % Modulation order
x = (0:15);                   % Integer input
symbin = qammod(x,M,'bin');   % 16-QAM output (binary-coded)
symgray = qammod(x,M,'gray'); % 16-QAM output (Gray-coded)

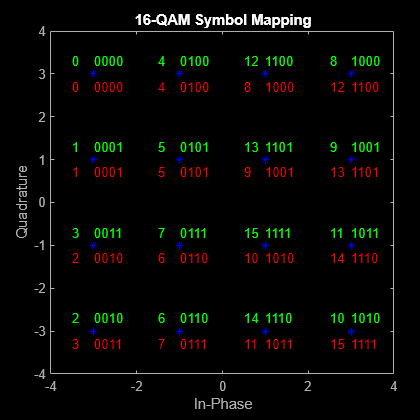
関数 scatterplot を使用して、コンスタレーションダイアグラムをプロットし、コンスタレーション点のバイナリ表現 (赤) とグレイ表現 (緑) で注釈を付けます。

scatterplot(symgray,1,0,'b*');
for k = 1:M
    text(real(symgray(k)) - 0.0,imag(symgray(k)) + 0.3, ...
        dec2base(x(k),2,4),'Color',[0 1 0]);
     text(real(symgray(k)) - 0.5,imag(symgray(k)) + 0.3, ...
         num2str(x(k)),'Color',[0 1 0]);
    
    text(real(symbin(k)) - 0.0,imag(symbin(k)) - 0.3, ...
        dec2base(x(k),2,4),'Color',[1 0 0]);
    text(real(symbin(k)) - 0.5,imag(symbin(k)) - 0.3, ...
        num2str(x(k)),'Color',[1 0 0]);
end
title('16-QAM Symbol Mapping')
axis([-4 4 -4 4])

プロットの確認

グレイ符号の信号コンスタレーション点は隣接する各近傍点と 1 ビットしか違いがないため、グレイ符号のシンボルマッピングを使用すると BER 性能が向上します。バイナリ符号のシンボルマッピングでは、隣接するコンスタレーション点のうち、2 つのビットが異なるものがあります。たとえば、バイナリ符号における値 1 (0 0 0 1) と値 2 (0 0 1 0) では 2 つのビットが異なっています (3 番目と 4 番目のビット)。

参考

関数

qammod | qamdemod | biterr | awgn

MATLAB を使用した 16-QAM の調査

ランダムな信号の変調

ランダムなバイナリ データ フレームの生成

バイナリ データから整数値のシンボルへの変換

16-QAM を使用した変調

ホワイト ガウス ノイズの追加

コンスタレーション ダイアグラムの作成