predict

線形回帰モデルの応答を予測

構文

ypred = predict(mdl,Xnew)

[ypred,yci] = predict(mdl,Xnew)

[ypred,yci] = predict(mdl,Xnew,Name,Value)

説明

ypred = predict(mdl,Xnew) は、Xnew 内の点に対して予測した線形回帰モデル mdl の応答値を返します。

[ypred,yci] = predict(mdl,Xnew) は、Xnew における応答の信頼区間も返します。

[ypred,yci] = predict(mdl,Xnew,Name,Value) では、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、信頼区間の信頼水準や予測タイプを指定できます。

例

応答値の予測

carsmall データ セットから、自動車の燃費の 2 次モデルを重量の関数として作成します。

load carsmall
X = Weight;
y = MPG;
mdl = fitlm(X,y,'quadratic');

データに対する予測された応答を作成します。

ypred = predict(mdl,X);

元の応答と予測された応答をプロットして、相違点を確認します。

plot(X,y,'o',X,ypred,'x')
legend('Data','Predictions')

予測用の C/C++ コードの生成

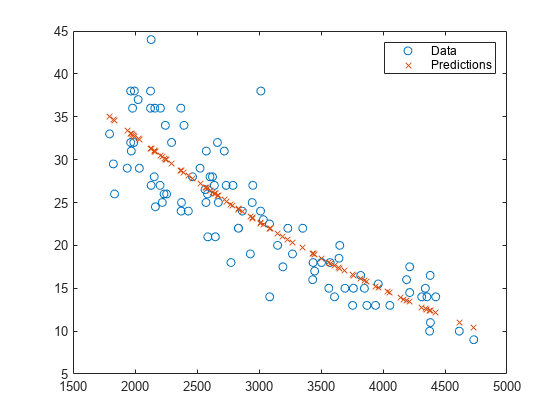
線形回帰モデルを当てはめてから、saveLearnerForCoderを使用してモデルを保存します。loadLearnerForCoderを使用してモデルを読み込み、当てはめたモデルの関数 predict を呼び出す、エントリポイント関数を定義します。その後、codegen (MATLAB Coder) を使用して C/C++ コードを生成します。C/C++ コードの生成には MATLAB® Coder™ が必要であることに注意してください。

この例では、コマンド ラインで線形回帰モデルの予測を行うためのコード生成ワークフローについて簡単に説明します。詳細は、機械学習モデルの予測をコマンド ラインで行うコードの生成を参照してください。MATLAB Coder アプリを使用してコードを生成することもできます。詳細については、機械学習モデルの予測を MATLAB Coder アプリを使用して行うコードの生成を参照してください。

モデルの学習

carsmall データ セットを読み込んで、2 次回帰モデルを当てはめます。

load carsmall
X = Weight;
y = MPG;
mdl = fitlm(X,y,'quadratic');

モデルの保存

saveLearnerForCoderを使用して、当てはめた 2 次モデルを QLMMdl.mat というファイルに保存します。

saveLearnerForCoder(mdl,'QLMMdl');

エントリポイント関数の定義

以下を行う mypredictQLM という名前のエントリポイント関数を定義します。

• X に対応する測定値と、オプションの有効な名前と値のペアの引数を受け入れる。

• QLMMdl.mat 内の当てはめ済み 2 次モデルを読み込む。

• 予測と信頼区間の範囲を返す。

function [yhat,ci] = mypredictQLM(x,varargin) %#codegen
%MYPREDICTQLM Predict response using linear model
%   MYPREDICTQLM predicts responses for the n observations in the n-by-1
%   vector x using the linear model stored in the MAT-file QLMMdl.mat, and
%   then returns the predictions in the n-by-1 vector yhat. MYPREDICTQLM
%   also returns confidence interval bounds for the predictions in the
%   n-by-2 vector ci.
CompactMdl = loadLearnerForCoder('QLMMdl');
[yhat,ci] = predict(CompactMdl,x,varargin{:});
end

MATLAB のアルゴリズムについてのコードを生成しようとしていることを指示するため、コンパイラ命令 %#codegen (またはプラグマ) をエントリポイント関数のシグネチャの後に追加します。この命令を追加すると、MATLAB Code Analyzer はコード生成時にエラーになる違反の診断と修正を支援します。

メモ: この例の右上にあるボタンをクリックして MATLAB® で例を開くと、MATLAB は例のフォルダーを開きます。このフォルダーには、エントリポイント関数のファイルが含まれています。

コードの生成

codegen (MATLAB Coder) を使用して、エントリポイント関数のコードを生成します。C および C++ は静的な型の言語なので、エントリポイント関数内のすべての変数のプロパティをコンパイル時に決定しなければなりません。データ型と正確な入力配列のサイズを指定するため、特定のデータ型および配列サイズをもつ一連の値を表す MATLAB® 式を渡します。名前と値のペアの引数の名前に対してcoder.Constant (MATLAB Coder)を使用します。

コンパイル時に観測値の個数が不明である場合、coder.typeof (MATLAB Coder) を使用して可変サイズの入力を指定することもできます。詳細は、コード生成用の可変サイズ引数の指定 と エントリポイント関数の入力の型の指定 (MATLAB Coder) を参照してください。

codegen mypredictQLM -args {X,coder.Constant('Alpha'),0.1,coder.Constant('Simultaneous'),true}

Code generation successful.

codegen は、プラットフォームに依存する拡張子をもつ MEX 関数 mypredictQLM_mex を生成します。

生成されたコードの確認

predict と mypredictQLM_mex を使用して、予測および信頼区間を比較します。codegen を呼び出したときの引数 -args と同じ順序で名前と値のペアの引数を指定します。

Xnew = sort(X);
[yhat1,ci1] = predict(mdl,Xnew,'Alpha',0.1,'Simultaneous',true);
[yhat2,ci2] = mypredictQLM_mex(Xnew,'Alpha',0.1,'Simultaneous',true);

predict から返された値と比較すると、mypredictQLM_mex から返された値には、丸めによる差が含まれている可能性があります。このような場合は、小さい誤差を許容して値を比較します。

find(abs(yhat1-yhat2) > 1e-6)

ans =

  0×1 empty double column vector

find(abs(ci1-ci2) > 1e-6)

ans =

  0×1 empty double column vector

この比較により、返された値が許容誤差 1e–6 内で等しいことを確認します。

比較のため、返された値をプロットします。

h1 = plot(X,y,'k.');
hold on
h2 = plot(Xnew,yhat1,'ro',Xnew,yhat2,'gx');
h3 = plot(Xnew,ci1,'r-','LineWidth',4);
h4 = plot(Xnew,ci2,'g--','LineWidth',2);
legend([h1; h2; h3(1); h4(1)], ...
    {'Data','predict estimates','MEX estimates','predict CIs','MEX CIs'});
xlabel('Weight');
ylabel('MPG');

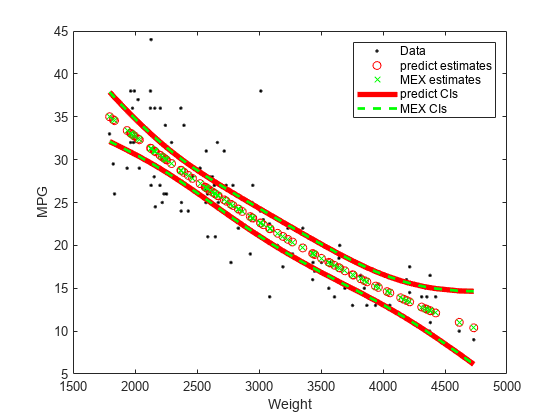
入力引数

mdl — 線形回帰モデル オブジェクト

LinearModel オブジェクト | CompactLinearModel オブジェクト

線形回帰モデル オブジェクト。fitlm または stepwiselm を使用して作成した LinearModel オブジェクト、または compact を使用して作成した CompactLinearModel オブジェクトとして指定します。

Xnew — 新しい予測子の入力値

table | 行列

新しい予測子の入力値。table または行列として指定します。Xnew の各行は 1 つの観測値に対応し、各列は 1 つの変数に対応します。

• Xnew が table である場合、mdl の PredictorNames プロパティの予測子と同じ名前の予測子が含まれていなければなりません。

• Xnew が行列である場合、mdl の作成に使用した予測子入力と同じ個数の変数 (列) が同じ順序で含まれていなければなりません。mdl の作成に使用する変数は、すべて数値でなければなりません。数値予測子をカテゴリカルとして扱うには、mdl を作成するときに名前と値の引数 CategoricalVars を使用して予測子を指定します。

当てはめたモデルで予測子として使用されない予測子変数も Xnew にすべて含めなければならないことに注意してください。

データ型: single | double | table

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: [ypred,yci] = predict(Mdl,Xnew,'Alpha',0.01,'Simultaneous',true) は、すべての予測子の値について同時に計算した、信頼水準が 99% である信頼区間 yci を返します。

Alpha — 有意水準

0.05 (既定値) | 範囲 [0,1] の数値

信頼区間の有意水準。範囲 [0,1] の数値を指定します。yci の信頼水準は 100(1 – Alpha)% に等しい値です。Alpha は、真の値が信頼区間に含まれない確率です。

例: Alpha=0.01

データ型: single | double

Prediction — 予測タイプ

"curve" (既定値) | "observation"

予測のタイプ。"curve" または "observation" として指定します。

予測子変数 X と応答変数 y に対する回帰モデルは、次の形式になります。

y = f(X) + ε,

ここで、f は当てはめた回帰関数、ε はランダムなノイズ項です。

• Prediction が "curve" である場合、関数は Xnew における当てはめた応答 f(Xnew) に対する信頼限界を予測します。

• Prediction が "observation" である場合、関数は Xnew における応答観測値 y に対する信頼限界を予測します。

ノイズ項により変動性が追加されるので、y の範囲は f(X) の範囲より広くなります。

例: Prediction="observation"

データ型: string | char

Simultaneous — 同時信頼限界を計算するためのフラグ

false または 0 (既定値) | true または 1

同時信頼限界を計算するフラグ。数値または logical の 1 (true) または 0 (false) として指定します。

• true — predict は、シェッフェの方法を使用して、Xnew 内のすべての予測子の値に対応する応答値の曲線に対して信頼限界を計算します。上限と下限の間の範囲には、真の応答値から構成される曲線が 100(1 – α)% の信頼度で含まれます。

• false — predict は、Xnew 内の各観測値における応答値に対して信頼限界を計算します。特定の予測子の値における応答値の信頼区間には、真の応答値が 100(1 – α)% の信頼度で含まれます。

同時区間では、真の応答値の曲線全体が高い信頼度で範囲内に収まります。一方、非同時区間では、高い信頼度で範囲内に収まる必要があるのは単一の予測子の値における応答値だけです。したがって、同時区間の方が非同時区間より広くなります。

例: Simultaneous=true

出力引数

ypred — 予測した応答の値

数値ベクトル

Xnew で予測した応答の値。数値ベクトルとして返されます。

yci — 応答の信頼区間

2 列の数値行列

応答の信頼区間。各行が 1 つの区間に対応する 2 列の行列として返されます。信頼区間の意味は、名前と値の引数 Alpha、Prediction、および Simultaneous の設定によって異なります。

代替機能

• feval は、predict と同じ予測を返します。関数 feval は、複数の入力引数を受け取ることができ、各予測子変数には 1 つの入力が対応します。table またはデータセット配列から作成したモデルの場合、この関数をより簡単に使用できます。関数 feval は、予測に対する信頼区間は返さないことに注意してください。

• random は、ノイズを追加した予測を返します。

• 予測した回帰面を通るスライスをそれぞれが表す一連のプロットが含まれている Figure を作成するには、plotSlice を使用します。各プロットは、他の予測子変数の値を固定した状態で単一の予測子変数の関数として当てはめた応答値を示します。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• saveLearnerForCoder、loadLearnerForCoder および codegen (MATLAB Coder) を使用して、関数 predict のコードを生成します。saveLearnerForCoder を使用して、学習済みモデルを保存します。loadLearnerForCoder を使用して保存済みモデルを読み込んで関数 predict を呼び出す、エントリポイント関数を定義します。次に、codegen を使用して、エントリポイント関数のコードを生成します。

• predict の単精度の C/C++ コードを生成するには、loadLearnerForCoder 関数を呼び出すときに DataType="single" を指定します。

• 次の表は、predict の引数に関する注意です。この表に含まれていない引数は、完全にサポートされています。

  引数	注意と制限
  mdl	fitlm を使用し、RobustWgtFun フィールドに無名関数ハンドルを設定した構造体を 'RobustOpts' に対して指定することにより線形モデルに学習をさせた場合に、saveLearnerForCoder を使用してモデルを保存してから、loadLearnerForCoder を使用してモデルを読み込んだとします。この場合、loadLearnerForCoder は Robust プロパティを MATLAB® ワークスペースに復元できません。しかし loadLearnerForCoder は、コード生成用のエントリポイント関数内でコンパイル時にモデルを読み込むことができます。 モデル オブジェクトの使用上の注意および制限については、CompactLinearModel オブジェクトのコード生成を参照してください。
  Xnew	Xnew は、単精度または倍精度の行列か、数値変数、カテゴリカル変数、またはその両方を含む table でなければなりません。 Xnew の行数、または観測値の数は可変サイズにすることができますが、Xnew の列数は固定でなければなりません。 Xnew を table として指定する場合、モデルは table を使用して学習させたものでなければならず、かつ予測のためのエントリポイント関数が次を行うようにしなければなりません。 データを配列として受け入れる データ入力の引数から table を作成し、その table 内で変数名を指定する table を predict に渡す この table のワークフローの例については、table のデータを分類するためのコードの生成を参照してください。コード生成における table の使用の詳細については、table のコード生成 (MATLAB Coder)およびコード生成における table の制限事項 (MATLAB Coder)を参照してください。
  名前と値のペアの引数	名前と値の引数に含まれる名前はコンパイル時の定数でなければなりません。たとえば、生成されたコードでユーザー定義の有意水準を可能にするには、{coder.Constant('Alpha'),0} を codegen (MATLAB Coder) の -args の値に含めます。

詳細は、コード生成の紹介を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2012a で導入

参考

CompactLinearModel | LinearModel | feval | random | plotSlice

トピック

• 新しいデータに対する応答を予測またはシミュレート
• 線形回帰ワークフロー
• 線形回帰の結果の解釈
• 線形回帰