incrementalRegressionKernel

インクリメンタル学習用のカーネル回帰モデル

R2022a 以降

説明

関数 incrementalRegressionKernel は incrementalRegressionKernel モデル オブジェクトを作成します。これは、インクリメンタル学習用のバイナリ ガウス カーネル回帰モデルを表します。このカーネル モデルは、低次元空間のデータを高次元空間にマッピングしてから、高次元空間で線形モデルを当てはめます。サポートされる線形モデルには、サポート ベクター マシン (SVM) 回帰と最小二乗回帰があります。

他の Statistics and Machine Learning Toolbox™ モデル オブジェクトとは異なり、incrementalRegressionKernel は直接呼び出すことができます。また、モデルをデータに当てはめる前に、パフォーマンス メトリクス構成や目的ソルバーなどの学習オプションを指定できます。incrementalRegressionKernel オブジェクトを作成すると、インクリメンタル学習用に準備されます。

incrementalRegressionKernel は、インクリメンタル学習に最適です。カーネル回帰モデルに学習させるための従来のアプローチ (データへの当てはめによるモデルの作成、交差検証の実行、ハイパーパラメーターの調整など) については、fitrkernel を参照してください。

作成

incrementalRegressionKernel モデル オブジェクトは、次のいくつかの方法で作成できます。

• 関数の直接呼び出し — incrementalRegressionKernel を直接呼び出して、インクリメンタル学習オプションを構成するか、学習器固有のオプションを指定します。このアプローチは、データがまだない場合やインクリメンタル学習をすぐに開始したい場合に最適です。

• 従来式の学習済みモデルの変換 — 学習済みモデル オブジェクト (RegressionKernel) のモデル パラメーターおよびハイパーパラメーターを使用してインクリメンタル学習用のモデルを初期化するには、従来式の学習済みモデルを関数 incrementalLearner に渡して incrementalRegressionKernel モデル オブジェクトに変換できます。

• インクリメンタル学習関数の呼び出し — fit、updateMetrics、および updateMetricsAndFit は、構成済みの incrementalRegressionKernel モデル オブジェクトおよびデータを入力として受け入れ、入力モデルとデータから学習した情報で更新された incrementalRegressionKernel モデル オブジェクトを返します。

構文

Mdl = incrementalRegressionKernel()

Mdl = incrementalRegressionKernel(Name=Value)

説明

Mdl = incrementalRegressionKernel() は、バイナリ ガウス カーネル回帰用の既定のインクリメンタル学習モデル オブジェクト Mdl を返します。既定のモデルのプロパティには、未知のモデル パラメーター用のプレースホルダーが含まれています。既定のモデルは、パフォーマンスを追跡したり、予測を生成したりする前に学習させなければなりません。

Mdl = incrementalRegressionKernel(Name=Value) は、名前と値の引数を使用して、プロパティと追加のオプションを設定します。たとえば、incrementalRegressionKernel(Solver="sgd",LearnRateSchedule="constant") は、確率的勾配降下 (SGD) ソルバーを一定の学習率で使用するように指定します。

入力引数

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後ろにする必要がありますが、ペアの順序は関係ありません。

例: Metrics="mse",MetricsWarmupPeriod=100 は、モデルのパフォーマンス メトリクスを重み付けされた平均二乗誤差、メトリクスのウォームアップ期間を 100 に設定します。

回帰のオプション

RandomStream — 乱数ストリーム

グローバル ストリーム (既定値) | 乱数ストリーム オブジェクト

データ変換の再現性を得るための乱数ストリーム。乱数ストリーム オブジェクトとして指定します。詳細については、ランダムな特徴量拡張を参照してください。

予測子データを高次元空間に変換するために incrementalRegressionKernel で使用されるランダムな基底関数を再現するには、RandomStream を使用します。詳細は、RandStream を使用したグローバル ストリームの管理 と 乱数ストリームの作成と管理 を参照してください。

例: RandomStream=RandStream("mlfg6331_64")

Standardize — 予測子データを標準化するためのフラグ

"auto" (既定値) | false | true

R2023b 以降

予測子データを標準化するためのフラグ。次の表の値として指定します。

値	説明
"auto"	incrementalRegressionKernel が予測子変数を標準化する必要があるかどうかを決定します。データの標準化を参照してください。
true	ソフトウェアが予測子データを標準化します。詳細については、データの標準化を参照してください。
false	ソフトウェアが予測子データを標準化しません。

例: Standardize=true

データ型: logical | char | string

SGD ソルバーと ASGD (平均化 SGD) ソルバーのオプション

BatchSize — ミニバッチのサイズ

10 (既定値) | 正の整数

ミニバッチのサイズ。正の整数として指定します。学習中の各学習サイクルで、incrementalRegressionKernel は BatchSize 個の観測値を使用して劣勾配を計算します。

最後のミニバッチ (fit または updateMetricsAndFit の各関数呼び出しにおける最後の学習サイクル) に含まれる観測値の数は、BatchSize より小さくてもかまいません。たとえば、fit または updateMetricsAndFit に 25 個の観測値を指定した場合、関数は最初の 2 つの学習サイクルに 10 個の観測値を使用し、最後の学習サイクルに 5 の観測値を使用します。

例: BatchSize=5

データ型: single | double

Lambda — リッジ (L2) 正則化項の強度

1e-5 (既定値) | 非負のスカラー

リッジ (L2) 正則化項の強度。非負のスカラーとして指定します。

例: Lambda=0.01

データ型: single | double

LearnRate — 初期学習率

"auto" (既定値) | 正のスカラー

初期学習率。"auto" または正のスカラーとして指定します。

学習率は、目的の劣勾配をスケールすることによって最適化のステップ サイズを制御します。LearnRate は学習率の初期値を指定し、LearnRateSchedule によって後続の学習サイクルの学習率が決まります。

"auto" を指定した場合、次のようになります。

• 初期学習率は 0.7 となります。

• EstimationPeriod > 0 の場合、fit および updateMetricsAndFit は、EstimationPeriod の最後にこの比率を 1/sqrt(1+max(sum(X.^2,2))) に変更します。

例: LearnRate=0.001

データ型: single | double | char | string

LearnRateSchedule — 学習率スケジュール

"decaying" (既定値) | "constant"

学習率スケジュール。次の表の値として指定します。ここで、LearnRate は初期学習率 ɣ₀ を指定します。

値	説明
"constant"	すべての学習サイクルの学習率を ɣ0 とする。
"decaying"	学習サイクル t での学習率を次とする。 $${\gamma }_t=\frac{{\gamma }_0}{{\left(1+\lambda {\gamma }_{0}t\right)}^c}.$$ λ は Lambda の値です。 Solver が "sgd" の場合、c = 1 です。 Solver が "asgd" の場合、次のようになります。 Learner が "leastsquares" の場合は c = 2/3。 Learner が "svm" の場合は c = 3/4 [4]。

例: LearnRateSchedule="constant"

データ型: char | string

適応型スケール不変ソルバーのオプション

Shuffle — 観測値のシャッフル フラグ

true または 1 (既定値) | false または 0

各反復での観測値のシャッフル フラグ。logical 1 (true) または 0 (false) として指定します。

値	説明
logical 1 (true)	ソフトウェアが、関数 fit でモデルを当てはめる前に、データの入力チャンク内の観測値をシャッフルします。このアクションにより、抽出スキームによって誘発されるバイアスが低減されます。
logical 0 (false)	ソフトウェアが、受信した順序でデータを処理します。

例: Shuffle=false

データ型: logical

パフォーマンス メトリクス オプション

Metrics — インクリメンタル学習中に追跡するモデルのパフォーマンス メトリクス

"epsiloninsensitive" | "mse" | string ベクトル | 関数ハンドル | cell ベクトル | 構造体配列

インクリメンタル学習中に追跡するモデルのパフォーマンス メトリクス。組み込みの損失関数の名前、名前の string ベクトル、関数ハンドル (@metricName)、関数ハンドルの構造体配列、または名前、関数ハンドル、構造体配列の cell ベクトルとして指定します。

Mdl が "ウォーム" のとき (IsWarm を参照)、updateMetrics および updateMetricsAndFit は Mdl の Metrics プロパティのパフォーマンス メトリクスを追跡します。

次の表は、組み込みの損失関数名と、それらをサポートする学習器 (Learner で指定) の一覧です。string ベクトルを使用して、複数の損失関数を指定できます。

名前	説明	メトリクスをサポートする学習器
"epsiloninsensitive"	イプシロン不感応損失	"svm"
"mse"	重み付けされた平均二乗誤差	"svm" および "leastsquares"

組み込み損失関数の詳細については、loss を参照してください。

例: Metrics=["epsiloninsensitive","mse"]

パフォーマンス メトリクスを返すカスタム関数を指定するには、関数ハンドル表記を使用します。関数は次の形式でなければなりません。

metric = customMetric(Y,YFit)

• 出力引数 metric は n 行 1 列の数値ベクトルです。ここで、各要素は、学習サイクル中にインクリメンタル学習関数によって処理されたデータの対応する観測値の損失です。

• 関数名 (customMetric) を指定します。

• Y は、観測応答の長さ n の数値ベクトルです。ここで、n は標本サイズです。

• YFit は、対応する予測応答の長さ n の数値ベクトルです。

複数のカスタム メトリクスを指定し、それぞれにカスタム名を割り当てるには、構造体配列を使用します。組み込みメトリクスとカスタム メトリクスの組み合わせを指定するには、cell ベクトルを使用します。

例: Metrics=struct(Metric1=@customMetric1,Metric2=@customMetric2)

例: Metrics={@customMetric1,@customMetric2,"mse",struct(Metric3=@customMetric3)}

updateMetrics および updateMetricsAndFit は、table で指定したメトリクスをプロパティ Metrics に保存します。Metrics のデータ型によって、table の行名が決まります。

Metrics 値のデータ型	Metrics プロパティの行名の説明	例
string または文字ベクトル	対応する組み込みメトリクスの名前	"epsiloninsensitive" の行名は "EpsilonInsensitiveLoss"
構造体配列	フィールド名	struct(Metric1=@customMetric1) の行名は "Metric1"
プログラム ファイルに格納されている関数への関数ハンドル	関数名	@customMetric の行名は "customMetric"
無名関数	CustomMetric_j。ここで、j は Metrics のメトリクス j	@(Y,YFit)customMetric(Y,YFit)... の行名は CustomMetric_1

既定の設定では、次のようになります。

• Learner が "svm" の場合、Metrics は "epsiloninsensitive" です。

• Learner が "leastsquares" の場合、Metrics は "mse" です。

パフォーマンス メトリクス オプションの詳細については、パフォーマンス メトリクスを参照してください。

データ型: char | string | struct | cell | function_handle

プロパティ

ほとんどのプロパティは、incrementalRegressionKernel を呼び出すときに名前と値の引数の構文を使用して直接設定できます。incrementalLearner を呼び出して従来式の学習済みモデルを変換するときに、いくつかのプロパティを設定できます。プロパティ FittedLoss、NumTrainingObservations、SolverOptions、および IsWarm は設定できません。

回帰モデルのパラメーター

Epsilon — イプシロン不感応区間の幅の半分

"auto" | 非負のスカラー

この プロパティ は読み取り専用です。

イプシロン不感応区間の幅の半分。"auto" または非負のスカラーとして指定します。incrementalRegressionKernel は Epsilon 値を数値スカラーとして格納します。

incrementalRegressionKernel を呼び出すときに "auto" を指定した場合、インクリメンタル近似関数は次の手順を使用して、EstimationPeriod で指定される推定期間中に Epsilon を推定します。

• iqr(Y) ≠ 0 の場合、Epsilon は iqr(Y)/13.49 です。ここで、Y は推定期間の応答データです。

• iqr(Y) = 0 であるか Mdl をデータに当てはめる前の場合、Epsilon は 0.1 です。

Epsilon の既定値は、モデルの作成方法に応じて異なります。

• Learner プロパティが 'svm' である従来式の学習済みモデルを変換する場合、Epsilon は従来式の学習済みモデルの対応するプロパティによって指定されます。

• それ以外の場合、既定値は "auto" です。

Learner が "leastsquares" の場合、Epsilon を設定することはできず、その値は NaN になります。

データ型: single | double

FittedLoss — 線形モデルの当てはめに使用する損失関数

'epsiloninsensitive' | 'mse'

この プロパティ は読み取り専用です。

線形モデルの当てはめに使用する損失関数。'epsiloninsensitive' または 'mse' を指定します。

値	アルゴリズム	損失関数	Learner の値
'epsiloninsensitive'	サポート ベクター マシン回帰	イプシロン不感応: $$\ell \left[y,f\left(x\right)\right]=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right]$$	'svm'
'mse'	通常の最小二乗による線形回帰	平均二乗誤差 (MSE): $$\ell \left[y,f\left(x\right)\right]=\frac{1}{2}{\left[y-f\left(x\right)\right]}^2$$	'leastsquares'

KernelScale — カーネル スケール パラメーター

"auto" | 正のスカラー

この プロパティ は読み取り専用です。

カーネル スケール パラメーター。"auto" または正のスカラーとして指定します。incrementalRegressionKernel は KernelScale 値を数値スカラーとして格納します。カーネル スケール パラメーターを使用して、特徴量拡張用のランダムな基底が取得されます。詳細については、ランダムな特徴量拡張を参照してください。

モデル オブジェクトの作成時に "auto" を指定した場合、ヒューリスティック手法を使用して適切なカーネル スケール パラメーターが選択されます。この手法では副標本抽出を使用するので、呼び出すたびに推定値が変化する可能性があります。このため、結果を再現するには、学習の前に rng を使用して乱数シードを設定します。

KernelScale の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、KernelScale は従来式の学習済みモデルの対応するプロパティによって指定されます。

• それ以外の場合、既定値は 1 です。

データ型: char | string | single | double

Learner — 線形回帰モデルのタイプ

"svm" | "leastsquares"

この プロパティ は読み取り専用です。

線形回帰モデルのタイプ。"svm" または "leastsquares" として指定します。incrementalRegressionKernel は Learner 値を文字ベクトルとして格納します。

次の表では $$f\left(x\right)=T(x)\beta +b.$$ です。

• x は p 個の予測子変数による観測値 (行ベクトル) です。

• $$T(·)$$ は特徴量を拡張するための観測値 (行ベクトル) の変換です。T(x) は $${ℝ}^p$$ の x を高次元空間 ($${ℝ}^m$$) にマッピングします。

• β は係数のベクトルです。

• b はスカラー バイアスです。

値	アルゴリズム	損失関数	FittedLoss の値
"svm"	サポート ベクター マシン回帰	イプシロン不感応: $$\ell \left[y,f\left(x\right)\right]=\max \left[0,\left|y-f\left(x\right)\right|-\epsilon \right]$$	'epsiloninsensitive'
"leastsquares"	通常の最小二乗による線形回帰	平均二乗誤差 (MSE): $$\ell \left[y,f\left(x\right)\right]=\frac{1}{2}{\left[y-f\left(x\right)\right]}^2$$	'mse'

Learner の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、Learner は従来式の学習済みモデルの対応するプロパティによって指定されます。

• それ以外の場合、既定値は "svm" です。

NumExpansionDimensions — 拡張空間の次元数

"auto" | 正の整数

この プロパティ は読み取り専用です。

拡張空間の次元数。"auto" または正の整数として指定します。incrementalRegressionKernel は NumExpansionDimensions 値を数値スカラーとして格納します。

"auto" の場合、2.^ceil(min(log2(p)+5,15)) を使用して次元数が選択されます。p は予測子の数です。詳細については、ランダムな特徴量拡張を参照してください。

NumExpansionDimensions の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、NumExpansionDimensions は従来式の学習済みモデルの対応するプロパティによって指定されます。

• それ以外の場合、既定値は "auto" です。

データ型: char | string | single | double

NumPredictors — 予測子変数の数

非負の数値スカラー

この プロパティ は読み取り専用です。

予測子変数の数。非負の数値スカラーとして指定します。

NumPredictors の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、NumPredictors は従来式の学習済みモデルの対応するプロパティによって指定されます。

• incrementalRegressionKernel を直接呼び出して Mdl を作成する場合、NumPredictors は名前と値の引数の構文を使用して指定できます。値を指定しない場合、既定値は 0 で、インクリメンタル近似関数は学習中に予測子データから NumPredictors を推測します。

データ型: double

NumTrainingObservations — インクリメンタル モデルに当てはめる観測値の数

0 (既定値) | 非負の数値スカラー

この プロパティ は読み取り専用です。

インクリメンタル モデル Mdl に当てはめる観測値の数。非負の数値スカラーとして指定します。NumTrainingObservations は、Mdl および学習データを fit または updateMetricsAndFit に渡すときに増加します。

メモ

従来式の学習済みモデルを変換して Mdl を作成する場合、incrementalRegressionKernel は、従来式の学習済みモデルに当てはめる観測値の数を NumTrainingObservations に追加しません。

データ型: double

ResponseTransform — 応答変換関数

"none" | 関数ハンドル

この プロパティ は読み取り専用です。

応答変換関数。"none" または関数ハンドルとして指定します。incrementalRegressionKernel は ResponseTransform 値を文字ベクトルまたは関数ハンドルとして格納します。

ResponseTransform は、インクリメンタル学習関数が生の応答値を変換する方法を記述します。

MATLAB^® 関数やユーザー定義関数の場合は、関数ハンドルを入力します。たとえば、ResponseTransform=@function では、function が n 行 1 列のベクトル (元の応答) を受け入れ、同じ長さのベクトル (変換された応答) を返します。

ResponseTransform の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、ResponseTransform は従来式の学習済みモデルの対応するプロパティによって指定されます。

• それ以外の場合、既定値は "none" です。

データ型: char | string | function_handle

学習パラメーター

EstimationPeriod — ハイパーパラメーターの推定のために処理する観測値の数

非負の整数

この プロパティ は読み取り専用です。

ハイパーパラメーターの推定のために、パフォーマンス メトリクスの学習または追跡の前にインクリメンタル モデルが処理する観測値の数。非負の整数として指定します。

メモ

• Mdl をインクリメンタル学習用に準備する場合 (学習に必要なすべてのハイパーパラメーターを指定する必要があります)、incrementalRegressionKernel は EstimationPeriod を 0 に強制します。

• Mdl をインクリメンタル学習用に準備しない場合、incrementalRegressionKernel は EstimationPeriod を 1000 に設定します。

詳細については、推定期間を参照してください。

データ型: single | double

Mu — 予測子の平均

数値ベクトル | []

R2023b 以降

この プロパティ は読み取り専用です。

予測子の平均。数値ベクトルを指定します。

Mu が空の配列 [] で、Standardize=true が指定されている場合、インクリメンタル近似関数は、Mu を EstimationPeriod で指定された推定期間中に推定された予測子変数の平均に設定します。

Mu を直接指定することはできません。

データ型: single | double

Sigma — 予測子の標準偏差

数値ベクトル | []

R2023b 以降

この プロパティ は読み取り専用です。

予測子の標準偏差。数値ベクトルを指定します。

Sigma が空の配列 [] で、Standardize=true が指定されている場合、インクリメンタル近似関数は、Sigma を EstimationPeriod で指定された推定期間中に推定された予測子変数の標準偏差に設定します。

Sigma を直接指定することはできません。

データ型: single | double

Solver — 目的関数の最小化手法

"scale-invariant" | "sgd" | "asgd"

この プロパティ は読み取り専用です。

目的関数の最小化手法。"scale-invariant"、"sgd"、または "asgd" として指定します。incrementalRegressionKernel は Solver 値を文字ベクトルとして格納します。

値	説明	メモ:
"scale-invariant"	インクリメンタル学習用の適応型スケール不変ソルバー[1]	このアルゴリズムはパラメーターを持たず、予測子のスケールの違いに適応できます。SGD または ASGD を使用する前に、このアルゴリズムを試してください。 関数 fit でモデルを当てはめる前にデータの入力チャンクをシャッフルするには、Shuffle を true に設定します。
"sgd"	確率的勾配降下法 (SGD) [2][3]	SGD で効果的に学習させるには、データを標準化し、SGD ソルバーと ASGD (平均化 SGD) ソルバーのオプションにリストされているオプションを使用してハイパーパラメーターの適切な値を指定します。 関数 fit でモデルを当てはめる前にデータの入力チャンクが常にシャッフルされます。
"asgd"	平均化確率的勾配降下法 (ASGD) [4]	ASGD で効果的に学習させるには、データを標準化し、SGD ソルバーと ASGD (平均化 SGD) ソルバーのオプションにリストされているオプションを使用してハイパーパラメーターの適切な値を指定します。 関数 fit でモデルを当てはめる前にデータの入力チャンクが常にシャッフルされます。

Solver の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 Solver で行います。この引数の既定値は "scale-invariant" です。

• それ以外の場合、既定値は "scale-invariant" です。

データ型: char | string

SolverOptions — 目的ソルバーの構成

構造体配列

この プロパティ は読み取り専用です。

目的ソルバーの構成。構造体配列として指定します。SolverOptions のフィールドは Solver に応じて異なります。

• SGD ソルバーおよび ASGD ソルバーの場合、構造体配列に Solver、BatchSize、Lambda、LearnRate、および LearnRateSchedule のフィールドが含まれます。

• 適応型スケール不変ソルバーの場合、構造体配列に Solver および Shuffle のフィールドが含まれます。

フィールドの値は、incrementalRegressionKernel を直接呼び出してモデル オブジェクトを作成するとき、または関数 incrementalLearner を使用して従来式の学習済みモデルを変換するときに、対応する名前と値の引数を使用して指定できます。

データ型: struct

パフォーマンス メトリクス パラメーター

IsWarm — モデルがパフォーマンス メトリクスを追跡するかどうかを示すフラグ

false または 0 | true または 1

この プロパティ は読み取り専用です。

インクリメンタル モデルがパフォーマンス メトリクスを追跡するかどうかを示すフラグ。logical 0 (false) または 1 (true) として指定します。

インクリメンタル モデル Mdl は、インクリメンタル近似関数が (EstimationPeriod + MetricsWarmupPeriod) 個の観測値をインクリメンタル モデルに当てはめた後、"ウォーム" (IsWarm が true となる) になります。

値	説明
true または 1	インクリメンタル モデル Mdl がウォームです。この結果、updateMetrics および updateMetricsAndFit が Mdl の Metrics プロパティのパフォーマンス メトリクスを追跡します。
false または 0	updateMetrics および updateMetricsAndFit はパフォーマンス メトリクスを追跡しません。

データ型: logical

Metrics — モデルのパフォーマンス メトリクス

テーブル

この プロパティ は読み取り専用です。

updateMetrics および updateMetricsAndFit によってインクリメンタル学習中に更新されたモデルのパフォーマンス メトリクス。m 行 2 列の table として指定します。ここで、m は、名前と値の引数 Metrics によって指定されたメトリクスの数です。

Metrics の列には Cumulative および Window のラベルが付けられます。

• Cumulative:要素 j は、メトリクス j で測定される、モデルがウォーム (IsWarm が 1) になった時点からの、モデルの性能です。

• Window:要素 j は、メトリクス j で測定され、MetricsWindowSize プロパティで指定されたウィンドウ内のすべての観測値に対して評価される、モデルの性能です。ソフトウェアは MetricsWindowSize 個の観測値を処理した後、Window を更新します。

行には、指定したメトリクスのラベルが付けられます。詳細については、incrementalLearner または incrementalRegressionKernel の名前と値の引数 Metrics を参照してください。

データ型: table

MetricsWarmupPeriod — パフォーマンス メトリクスを追跡する前に当てはめる観測値の数

非負の整数

この プロパティ は読み取り専用です。

インクリメンタル モデルが Metrics プロパティのパフォーマンス メトリクスを追跡する前に当てはめなければならない観測値の数。非負の整数として指定します。

MetricsWarmupPeriod の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 MetricsWarmupPeriod で行います。この引数の既定値は 0 です。

• それ以外の場合、既定値は 1000 です。

詳細については、パフォーマンス メトリクスを参照してください。

データ型: single | double

MetricsWindowSize — ウィンドウ パフォーマンス メトリクスの計算に使用する観測値の数

正の整数

この プロパティ は読み取り専用です。

ウィンドウ パフォーマンス メトリクスの計算に使用する観測値の数。正の整数として指定します。

MetricsWindowSize の既定値は、モデルの作成方法に応じて異なります。

• 従来式の学習済みモデルを変換して Mdl を作成する場合、このプロパティの設定は関数 incrementalLearner の名前と値の引数 MetricsWindowSize で行います。この引数の既定値は 200 です。

• それ以外の場合、既定値は 200 です。

パフォーマンス メトリクス オプションの詳細については、パフォーマンス メトリクスを参照してください。

データ型: single | double

オブジェクト関数

fit	インクリメンタル学習用のカーネル モデルの学習
updateMetrics	カーネル インクリメンタル学習モデルの新しいデータに基づくパフォーマンス メトリクスの更新
updateMetricsAndFit	カーネル インクリメンタル学習モデルの新しいデータに基づくパフォーマンス メトリクスの更新とモデルの学習
loss	データのバッチでのカーネル インクリメンタル学習モデルの損失
predict	カーネル インクリメンタル学習モデルからの新しい観測の応答予測
perObservationLoss	インクリメンタル学習用モデルの観測値ごとの回帰誤差
reset	インクリメンタル回帰モデルのリセット

例

事前情報なしでのインクリメンタル学習器の作成

事前情報なしでインクリメンタル カーネル モデルを作成します。モデルの性能をストリーミング データで追跡し、モデルをデータに当てはめます。

回帰用の既定のインクリメンタル カーネル SVM モデルを作成します。

Mdl = incrementalRegressionKernel()

Mdl = 
  incrementalRegressionKernel

                    IsWarm: 0
                   Metrics: [1x2 table]
         ResponseTransform: 'none'
    NumExpansionDimensions: 0
               KernelScale: 1

Mdl.EstimationPeriod

ans = 1000

Mdl は incrementalRegressionKernel モデル オブジェクトです。そのプロパティはすべて読み取り専用です。

Mdl は、他の演算の実行に使用する前に、データに当てはめなければなりません。推定期間は、イプシロン不感応区間 Epsilon の幅の半分が不明であるため 1000 に設定されます。名前と値の引数 Epsilon を使用して Epsilon を正の浮動小数点スカラーに設定できます。このアクションにより、推定期間が既定の 0 になります。

ロボット アームのデータ セットを読み込みます。

load robotarm

データ セットの詳細については、コマンド ラインで Description を入力してください。

関数 updateMetricsAndFit を使用して、インクリメンタル モデルを学習データに当てはめます。一度に 50 個の観測値のチャンクにモデルを当てはめて、データ ストリームをシミュレートします。各反復で次を行います。

• 50 個の観測値を処理。

• 前のインクリメンタル モデルを、入力観測値に当てはめた新しいモデルで上書き。

• 累積メトリクス、ウィンドウ メトリクス、および学習観測値の数を保存し、インクリメンタル学習中にそれらがどのように進化するかを確認。

% Preallocation
n = numel(ytrain);
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ei = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); 
numtrainobs = zeros(nchunk+1,1);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,Xtrain(idx,:),ytrain(idx));
    ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:};
    numtrainobs(j+1) = Mdl.NumTrainingObservations;
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalRegressionKernel モデル オブジェクトです。updateMetricsAndFit は、最初の 1000 個の観測値の処理で Epsilon を推定するための応答値を格納します。この推定期間が経過するまではモデルは当てはめられません。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetricsAndFit は入力観測値でモデルの性能をチェックし、モデルをその観測値に当てはめます。

学習観測値の数とパフォーマンス メトリクスのトレース プロットを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(numtrainobs)
xlim([0 nchunk])
ylabel("Number of Training Observations")
xline(Mdl.EstimationPeriod/numObsPerChunk,"-.")
xline((Mdl.EstimationPeriod + Mdl.MetricsWarmupPeriod)/numObsPerChunk,"--")
nexttile
plot(ei.Variables)
xlim([0 nchunk])
ylabel("Epsilon Insensitive Loss")
xline(Mdl.EstimationPeriod/numObsPerChunk,"-.")
xline((Mdl.EstimationPeriod + Mdl.MetricsWarmupPeriod)/numObsPerChunk,"--")
legend(ei.Properties.VariableNames,Location="best")
xlabel(t,"Iteration")

プロットは、updateMetricsAndFit が次を行うことを示しています。

• 推定期間 (最初の 20 回の反復) の後、モデルをインクリメンタル学習のすべての反復で当てはめ。

• パフォーマンス メトリクスをメトリクスのウォームアップ期間後にのみ計算。

• 累積メトリクスを各反復中に計算。

• ウィンドウ メトリクスを 200 個の観測値 (4 回の反復) の処理後に計算。

インクリメンタル学習オプションの構成

メトリクスのウォームアップ期間とメトリクス ウィンドウ サイズを指定して、インクリメンタル回帰学習器を準備します。SGD を使用してモデルに学習させ、SGD バッチ サイズ、学習率、および正則化パラメーターを調整します。

ロボット アームのデータ セットを読み込みます。

load robotarm
n = numel(ytrain);

データ セットの詳細については、コマンド ラインで Description を入力してください。

回帰用のインクリメンタル カーネル モデルを作成します。次のようにモデルを構成します。

• SGD ソルバーを指定。

• リッジ正則化パラメーター値 0.001、SGD バッチ サイズ 20、学習率 0.002、および SVM のイプシロン不感応区間の幅の半分 0.05 という設定で、問題に対して十分に機能すると仮定。

• メトリクスのウォームアップ期間を観測値 1000 個に指定。

• メトリクス ウィンドウ サイズを観測値 500 個に指定。

• イプシロン不感応損失、MSE、および平均絶対誤差 (MAE) を追跡してモデルの性能を測定。ソフトウェアは、イプシロン不感応損失および MSE をサポートしています。新しい各観測値の絶対誤差を測定する無名関数を作成します。名前 MeanAbsoluteError とそれに対応する関数を含む構造体配列を作成します。

maefcn = @(z,zfit)abs(z - zfit);
maemetric = struct("MeanAbsoluteError",maefcn);

Mdl = incrementalRegressionKernel(Solver="sgd", ...
    Lambda=0.001,BatchSize=20,LearnRate=0.002,Epsilon=0.05, ...
    MetricsWarmupPeriod=1000,MetricsWindowSize=500, ...
    Metrics={"epsiloninsensitive","mse",maemetric})

Mdl = 
  incrementalRegressionKernel

                    IsWarm: 0
                   Metrics: [3x2 table]
         ResponseTransform: 'none'
    NumExpansionDimensions: 0
               KernelScale: 1

Mdl はインクリメンタル学習用に推定期間なしで構成された incrementalRegressionKernel モデル オブジェクトです。

関数 updateMetricsAndFit を使用して、インクリメンタル モデルをデータに当てはめます。各反復で次を行います。

• 50 個の観測値のチャンクを処理して、データ ストリームをシミュレート。チャンクのサイズと SGD バッチ サイズは異なることに注意してください。

• 前のインクリメンタル モデルを、入力観測値に当てはめた新しいモデルで上書き。

• 累積メトリクス、ウィンドウ メトリクス、および学習観測値の数を保存し、インクリメンタル学習中にそれらがどのように進化するかを確認。

% Preallocation
numObsPerChunk = 50;
nchunk = floor(n/numObsPerChunk);
ei = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
mse = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
mae = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);  
numtrainobs = zeros(nchunk,1);

% Incremental fitting
rng("default") % For reproducibility
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1);
    iend   = min(n,numObsPerChunk*j);
    idx = ibegin:iend;    
    Mdl = updateMetricsAndFit(Mdl,Xtrain(idx,:),ytrain(idx));
    ei{j,:} = Mdl.Metrics{"EpsilonInsensitiveLoss",:};
    mse{j,:} = Mdl.Metrics{"MeanSquaredError",:};
    mae{j,:} = Mdl.Metrics{"MeanAbsoluteError",:};
    numtrainobs(j) = Mdl.NumTrainingObservations;
end

Mdl は、ストリーム内のすべてのデータで学習させた incrementalRegressionKernel モデル オブジェクトです。インクリメンタル学習中およびモデルがウォームアップされた後、updateMetricsAndFit は入力観測値でモデルの性能をチェックし、モデルをその観測値に当てはめます。

学習観測値の数とパフォーマンス メトリクスのトレース プロットを別々のタイルにプロットします。

t = tiledlayout(4,1);
nexttile
plot(numtrainobs)
xlim([0 nchunk])
ylabel(["Number of","Training Observations"])
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--")
nexttile
plot(ei.Variables)
xlim([0 nchunk])
ylabel(["Epsilon Insensitive","Loss"])
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--")
legend(ei.Properties.VariableNames)
nexttile
plot(mse.Variables)
xlim([0 nchunk])
ylabel("MSE")
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--")
legend(mse.Properties.VariableNames)
nexttile
plot(mae.Variables)
xlim([0 nchunk])
ylabel("MAE")
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,"--")
legend(mae.Properties.VariableNames)
xlabel(t,"Iteration")

プロットは、updateMetricsAndFit が次を行うことを示しています。

• モデルをインクリメンタル学習のすべての反復で当てはめ。

• パフォーマンス メトリクスをメトリクスのウォームアップ期間後にのみ計算。

• 累積メトリクスを各反復中に計算。

• ウィンドウ メトリクスを 500 個の観測値 (10 回の反復) の処理後に計算。

従来式の学習済みモデルのインクリメンタル学習器への変換

fitrkernel を使用してカーネル回帰モデルに学習させ、それをインクリメンタル学習器に変換し、その性能を追跡し、ストリーミング データに当てはめます。学習オプションを従来式からインクリメンタル学習に引き継ぎます。

データの読み込みと前処理

2015 年のニューヨーク市住宅データ セットを読み込み、データをシャッフルします。このデータの詳細については、NYC Open Data を参照してください。

load NYCHousing2015
rng(1) % For reproducibility
n = size(NYCHousing2015,1);
idxshuff = randsample(n,n);
NYCHousing2015 = NYCHousing2015(idxshuff,:);

マンハッタンから収集されたデータ (BOROUGH = 1) が、品質を 2 倍にする新しい方法を使用して収集されたとします。マンハッタンから収集した観測値に 2 を割り当て、その他すべての観測値に 1 を割り当てる重み変数を作成します。

NYCHousing2015.W = ones(n,1) + (NYCHousing2015.BOROUGH == 1);

テーブルから応答変数 SALEPRICE を抽出します。数値安定性を得るために、SALEPRICE を 1e6 の尺度でスケールします。

Y = NYCHousing2015.SALEPRICE/1e6;
NYCHousing2015.SALEPRICE = [];

この例の計算コストを削減するために、254 個のカテゴリをもつカテゴリカル変数が含まれている NEIGHBORHOOD 列を削除します。

NYCHousing2015.NEIGHBORHOOD = [];

他のカテゴリカル予測子からダミー変数メトリクスを作成します。

catvars = ["BOROUGH","BUILDINGCLASSCATEGORY"];
dumvarstbl = varfun(@(x)dummyvar(categorical(x)),NYCHousing2015, ...
    InputVariables=catvars);
dumvarmat = table2array(dumvarstbl);
NYCHousing2015(:,catvars) = [];

テーブル内の他のすべての数値変数を売価の予測子として扱います。ダミー変数の行列を予測子データの残りに連結します。

idxnum = varfun(@isnumeric,NYCHousing2015,OutputFormat="uniform");
X = [dumvarmat NYCHousing2015{:,idxnum}];

カーネル回帰モデルの学習

カーネル回帰モデルを、データの半分から取った無作為標本に当てはめます。観測値の重みを指定します。

idxtt = randsample([true false],n,true);
Mdl = fitrkernel(X(idxtt,:),Y(idxtt),Weights=NYCHousing2015.W(idxtt))

Mdl = 
  RegressionKernel
              ResponseName: 'Y'
                   Learner: 'svm'
    NumExpansionDimensions: 2048
               KernelScale: 1
                    Lambda: 2.1977e-05
             BoxConstraint: 1
                   Epsilon: 0.0547

Mdl は従来式の学習済みカーネル回帰モデルを表す RegressionKernel モデル オブジェクトです。

学習済みモデルの変換

従来式の学習済みカーネル回帰モデルをインクリメンタル学習用のモデルに変換します。

IncrementalMdl = incrementalLearner(Mdl)

IncrementalMdl = 
  incrementalRegressionKernel

                    IsWarm: 1
                   Metrics: [1x2 table]
         ResponseTransform: 'none'
    NumExpansionDimensions: 2048
               KernelScale: 1

IncrementalMdl はインクリメンタル学習用に構成された incrementalRegressionKernel モデル オブジェクトです。

パフォーマンス メトリクスの追跡とモデルの当てはめの個別の実行

関数 updateMetrics および fit を使用して、残りのデータに対してインクリメンタル学習を実行します。500 個の観測値を一度に処理して、データ ストリームをシミュレートします。各反復で次を行います。

1. updateMetrics を呼び出し、観測値の入力チャンクを所与として、モデルのイプシロン不感応損失の累積とウィンドウを更新します。前のインクリメンタル モデルを上書きして、Metrics プロパティを更新します。関数がモデルをデータ チャンクに当てはめないことに注意してください。チャンクはモデルに対して "新しい" データです。観測値の重みを指定します。

2. fit を呼び出して、観測値の入力チャンクにモデルを当てはめます。前のインクリメンタル モデルを上書きして、モデル パラメーターを更新します。観測値の重みを指定します。

3. 損失と学習観測値の数を保存します。

% Preallocation
idxil = ~idxtt;
nil = sum(idxil);
numObsPerChunk = 500;
nchunk = floor(nil/numObsPerChunk);
ei = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]);
numtrainobs = zeros(nchunk,1);
Xil = X(idxil,:);
Yil = Y(idxil);
Wil = NYCHousing2015.W(idxil);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(nil,numObsPerChunk*(j-1) + 1);
    iend   = min(nil,numObsPerChunk*j);
    idx = ibegin:iend;
    IncrementalMdl = updateMetrics(IncrementalMdl,Xil(idx,:),Yil(idx), ...
        Weights=Wil(idx));
    ei{j,:} = IncrementalMdl.Metrics{"EpsilonInsensitiveLoss",:};
    IncrementalMdl = fit(IncrementalMdl,Xil(idx,:),Yil(idx), ...
        Weights=Wil(idx));
    numtrainobs(j) = IncrementalMdl.NumTrainingObservations;
end

IncrementalMdl は、ストリーム内のすべてのデータで学習させた incrementalRegressionKernel モデル オブジェクトです。

あるいは、updateMetricsAndFit を使用して、新しいデータ チャンクに対するモデルのパフォーマンス メトリクスを更新し、モデルをデータに当てはめることもできます。

学習観測値の数とパフォーマンス メトリクスのトレース プロットを別々のタイルにプロットします。

t = tiledlayout(2,1);
nexttile
plot(numtrainobs)
xlim([0 nchunk])
ylabel("Number of Training Observations")
nexttile
plot(ei.Variables)
xlim([0 nchunk])
ylabel("Epsilon Insensitive Loss")
legend(ei.Properties.VariableNames)
xlabel(t,"Iteration")

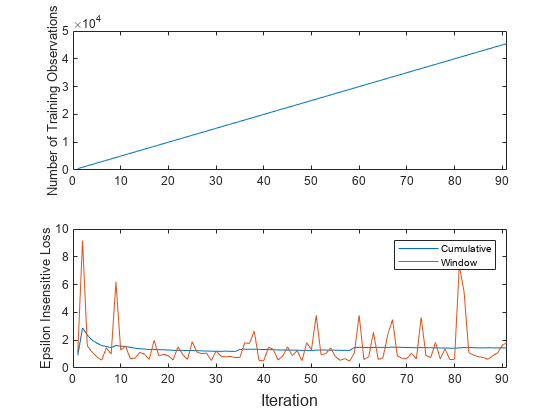
累積の損失は各反復 (500 個の観測値のチャンク) ごとに徐々に変化しますが、ウィンドウの損失には急な変動があります。メトリクス ウィンドウの既定値は 200 なので、updateMetrics は 500 個の観測値のチャンクごとに最新の 200 個の観測値に基づいて性能を測定します。

詳細

インクリメンタル学習

"インクリメンタル学習" ("オンライン学習") は、予測子変数の分布、予測関数や目的関数の素性 (調整パラメーターの値を含む)、観測値にラベル付けがされているか等についてほぼ知識が無い時に、データ ストリームから入ってくるデータを処理することに関係している機械学習の一分野です。従来の機械学習は、モデルへの当てはめに十分にラベル付けされたデータを使用でき、交差検証を実施してハイパーパラメーターを調整し、予測子の分布を推論するもので、インクリメンタル学習と異なります。

入力観測値に対し、インクリメンタル学習モデルは、次のいずれかの方法 (通常はこの順序) でデータを処理します。

• ラベルの予測。

• 予測性能の測定。

• モデルの構造的な破綻やドリフトについてのチェック。

• 入力観測値へのモデルの当てはめ。

詳細については、インクリメンタル学習の概要を参照してください。

インクリメンタル学習用の適応型スケール不変ソルバー

"インクリメンタル学習用の適応型スケール不変ソルバー" ([1]で紹介) は、線形予測モデルに学習させるための勾配降下法ベースの目的ソルバーです。ソルバーはハイパーパラメーターを持たず、予測子変数のスケールの違いの影響を受けず、予測子変数の分布の事前知識が不要です。これらの特徴は、インクリメンタル学習に適しています。

標準 SGD および ASGD ソルバーは、予測子変数間のスケールの違いの影響を受けやすいため、モデルの性能低下につながることがあります。SGD および ASGD を使用して精度を向上させるには、予測子データを標準化し、正則化と学習率のパラメーターを調整できます。従来の機械学習では、交差検証と予測子を標準化してハイパーパラメーター調整を行うのに十分なデータが利用できます。しかし、インクリメンタル学習の場合、十分なデータが利用できず (たとえば、観測値が一度に 1 つしか利用できない場合があります)、予測子の分布が未知である場合があります。このような特徴があるため、インクリメンタル学習中のパラメーター調整と予測子の標準化は困難または不可能です。

インクリメンタル近似関数 fit および updateMetricsAndFit は、アルゴリズムのより積極的な ScInOL2 バージョンを使用します。

ランダムな特徴量拡張

Random Kitchen Sink[1]や Fastfood[2]などのランダムな特徴量拡張は、ビッグ データに対するカーネル回帰アルゴリズムのガウス カーネルを計算効率が高い方法で近似する手法です。ランダムな特徴量拡張は、大規模な学習セットが含まれているビッグ データ事例に対する方が現実的ですが、メモリに収まる小規模なデータ セットにも適用できます。

カーネル回帰アルゴリズムでは、予測子データを高次元空間にマッピングした後で、各応答データ点 (y_i) からの逸脱がイプシロン マージン (ε) の値を超えない最適な関数を求めます。

一部の回帰問題は、線形モデルを使用して適切に表すことはできません。このような場合は、ドット積 x₁x₂′ を非線形カーネル関数 $$G(x_1,x_2)=\langle \phi (x_1),\phi (x_2)\rangle$$ に置き換えることにより非線形回帰モデルを取得します。ここで、x_i は i 番目の観測値 (行ベクトル)、φ(x_i) は x_i を高次元空間にマッピングする変換 ("カーネル トリック" と呼ばれます) です。しかし、(n が大きい) 大規模なデータ セットでは、観測値の各ペアについて G(x₁,x₂) (グラム行列) を評価すると計算コストが高くなります。

ランダムな特徴量拡張の方式では、ドット積がガウス カーネルを近似するようなランダム変換を求めます。つまり、次のようになります。

$$G(x_1,x_2)=\langle \phi (x_1),\phi (x_2)\rangle \approx T(x_1)T(x_2)\text{'},$$

ここで、T(x) は $${ℝ}^p$$ における x を高次元空間 ($${ℝ}^m$$) にマッピングします。Random Kitchen Sink[1]方式では、次のランダムな変換を使用します。

$$T(x)=m^{-1/2}\exp \left(iZx\text{'}\right)\text{'},$$

ここで、$$Z\in {ℝ}^{m\times p}$$ は $$N\left(0,{\sigma }^{-2}\right)$$ から抽出した標本、σ はカーネル スケールです。この方式では O(mp) の計算および格納が必要です。Fastfood[2]方式では、ガウス スケーリング行列と組み合わせたアダマール行列を使用して、Z の代わりに別のランダムな基底 V を導入します。このランダムな基底により、計算コストが O(mlogp) に、ストレージが O(m) に削減されます。

incrementalRegressionKernel は、ランダムな特徴量拡張に Fastfood 方式を使用し、線形回帰を使用してガウス カーネル回帰モデルに学習させます。m および σ の値は、fitrkernel を使用して従来式の学習済みモデルを作成するとき、または incrementalRegressionKernel を直接呼び出してモデル オブジェクトを作成するときに、名前と値の引数 NumExpansionDimensions および KernelScale を使用してそれぞれ指定できます。

アルゴリズム

推定期間

推定期間中、インクリメンタル近似関数 fit および updateMetricsAndFit は、最初の EstimationPeriod 個の入力観測値を使用して、インクリメンタル学習に必要なハイパーパラメーターを推定 (調整) します。推定は EstimationPeriod が正の場合にのみ発生します。次の表は、ハイパーパラメーターとそれらが推定または調整される条件について説明します。

ハイパーパラメーター	モデル プロパティ	使用法	条件
予測子の平均および標準偏差	Mu および Sigma	標準化された予測子データ	次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。 予測子データを標準化するようにインクリメンタル近似関数を構成 (データの標準化を参照)。 Mdl.Mu および Mdl.Sigma が空の配列 []。
学習率	SolverOptions の LearnRate フィールド	ソルバーのステップ サイズの調整	次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。 名前と値の引数 Solver を "sgd" または "asgd" として指定している。 名前と値の引数 LearnRate を正のスカラーとして指定していない。
イプシロン不感応区間の幅の半分	Epsilon	サポート ベクターの数の制御	次のいずれの条件にも当てはまる場合は、ハイパーパラメーターが推定されます。 関数 incrementalRegressionKernel を直接呼び出して incrementalRegressionKernel モデル オブジェクトを作成している。 学習器が SVM (Learner を参照)。 名前と値の引数 Epsilon を非負のスカラーとして指定していない。
カーネル スケール パラメーター	KernelScale	ランダムな特徴量拡張用のカーネル スケール パラメーターの値の設定	このハイパーパラメーターは、名前と値の引数 KernelScale を "auto" に設定した場合に推定されます。

推定期間中には、fit がモデルを当てはめることも、updateMetricsAndFit がモデルを当てはめたりパフォーマンス メトリクスを更新したりすることもありません。推定期間の満了時に、関数はハイパーパラメーターを格納するプロパティを更新します。

データの標準化

予測子変数を標準化するようにインクリメンタル学習関数が構成されている場合、インクリメンタル学習モデル Mdl の Mu プロパティと Sigma プロパティにそれぞれ保存されている平均と標準偏差を使用して標準化が行われます。

• Standardize=true と正の推定期間 (EstimationPeriod を参照) が設定されていて、Mdl.Mu と Mdl.Sigma が空の場合、インクリメンタル近似関数は、推定期間の観測値を使用して平均と標準偏差を推定します。

• Standardize="auto" を設定すると (既定の設定)、次の条件が適用されます。

  • 従来式の学習済みカーネル回帰モデル (RegressionKernel) を変換して incrementalRegressionKernel を作成する場合、変換元のモデルの Mu および Sigma プロパティが空の配列 [] であれば、インクリメンタル学習関数は予測子変数を標準化しません。変換元のモデルの Mu および Sigma プロパティが空でない場合、インクリメンタル学習関数は、指定された平均と標準偏差を使用して予測子変数を標準化します。インクリメンタル近似関数は、推定期間の長さにかかわらず、新しい平均と標準偏差を推定しません。

  • 従来式の学習済みモデルを変換するのでない場合、インクリメンタル学習関数は、SGD ソルバー (Solver を参照) と正の推定期間 (EstimationPeriod を参照) が指定されている場合にのみ予測子データを標準化します。

• インクリメンタル近似関数が予測子の平均と標準偏差を推定するとき、関数は推定期間の観測値を使用して加重平均と加重標準偏差を計算します。具体的には、関数は予測子 j (x_j) の標準化のために次を使用します。

  $$x_j^{\ast }=\frac{x_j-{\mu }_j^{\ast }}{{\sigma }_j^{\ast }}.$$

  • x_j は予測子 j、x_jk は推定期間内の予測子 j の観測値 k です。

  • $${\mu }_j^{\ast }=\frac{1}{{\displaystyle \sum _k{w}_k}}{\displaystyle \sum _k{w}_k{x}_{jk}}.$$

  • $${\left({\sigma }_j^{\ast }\right)}^2=\frac{1}{{\displaystyle \sum _k{w}_k}}{\displaystyle \sum _k{w}_k{\left(x_{jk}-{\mu }_j^{\ast }\right)}^2}.$$

  • w_j は観測値の重み j です。

パフォーマンス メトリクス

• 関数 updateMetrics および updateMetricsAndFit は、インクリメンタル モデルが "ウォーム" (IsWarm プロパティが true) のときにのみ、新しいデータからモデルのパフォーマンス メトリクス (Metrics) を追跡するインクリメンタル学習関数です。インクリメンタル モデルは、fit または updateMetricsAndFit がインクリメンタル モデルを MetricsWarmupPeriod 個の観測値 ("メトリクスのウォームアップ期間") に当てはめた後、ウォームになります。

  EstimationPeriod > 0 の場合、関数 fit および updateMetricsAndFit はモデルをデータに当てはめる前にハイパーパラメーターを推定します。そのため、関数は、モデルがメトリクスのウォームアップ期間を開始する前に EstimationPeriod 個の観測値を追加で処理しなければなりません。

• インクリメンタル モデルの Metrics プロパティは、各パフォーマンス メトリクスの 2 つの形式を table の変数 (列) Cumulative および Window とし、個々のメトリクスを行に格納します。インクリメンタル モデルがウォームになると、updateMetrics および updateMetricsAndFit は次の頻度でメトリクスを更新します。

  • Cumulative — 関数は、モデルの性能追跡の開始以降の累積メトリクスを計算します。関数は、関数が呼び出されるたびにメトリクスを更新し、提供されたデータ セット全体に基づいて計算を行います。

  • Window — 関数は、MetricsWindowSize によって決定されたウィンドウ内のすべての観測値に基づいてメトリクスを計算します。これによってソフトウェアが Window メトリクスを更新する頻度も決まります。たとえば、MetricsWindowSize が 20 の場合、関数は提供されたデータの最後の 20 個の観測値に基づいてメトリクスを計算します (X((end – 20 + 1):end,:) および Y((end – 20 + 1):end))。

    ウィンドウ内のパフォーマンス メトリクスを追跡するインクリメンタル関数は、次のプロセスを使用します。

    1. 指定された各メトリクスについて長さ MetricsWindowSize のバッファーを保存し、観測値の重みのバッファーを保存します。

    2. 入力観測値のバッチに基づくモデル性能をメトリクス バッファーの要素に入力し、対応する観測値の重みを重みバッファーに格納します。

    3. バッファーがいっぱいになると、Metrics プロパティの Window フィールドをメトリクス ウィンドウの性能の加重平均で上書きします。関数が観測値のバッチを処理するときにバッファーがあふれる場合、最新の入力観測値 MetricsWindowSize がバッファーに入り、最も古い観測値がバッファーから削除されます。たとえば、MetricsWindowSize が 20 で、メトリクス バッファーには前に処理されたバッチからの 10 個の値が存在し、15 個の値が入力されるとします。長さ 20 のウィンドウを構成するため、関数は 15 個の入力観測値からの測定値と前のバッチからの最新の 5 個の測定値を使用します。

• Cumulative と Window のパフォーマンス メトリクスの値を計算する際、予測が NaN の観測値は省略されます。

参照

[1] Kempka, Michał, Wojciech Kotłowski, and Manfred K. Warmuth. "Adaptive Scale-Invariant Online Algorithms for Learning Linear Models." Preprint, submitted February 10, 2019. https://arxiv.org/abs/1902.07528.

[2] Langford, J., L. Li, and T. Zhang. “Sparse Online Learning Via Truncated Gradient.” J. Mach. Learn. Res., Vol. 10, 2009, pp. 777–801.

[3] Shalev-Shwartz, S., Y. Singer, and N. Srebro. “Pegasos: Primal Estimated Sub-Gradient Solver for SVM.” Proceedings of the 24th International Conference on Machine Learning, ICML ’07, 2007, pp. 807–814.

[4] Xu, Wei. “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent.” CoRR, abs/1107.2490, 2011.

[5] Rahimi, A., and B. Recht. “Random Features for Large-Scale Kernel Machines.” Advances in Neural Information Processing Systems. Vol. 20, 2008, pp. 1177–1184.

[6] Le, Q., T. Sarlós, and A. Smola. “Fastfood — Approximating Kernel Expansions in Loglinear Time.” Proceedings of the 30th International Conference on Machine Learning. Vol. 28, No. 3, 2013, pp. 244–252.

[7] Huang, P. S., H. Avron, T. N. Sainath, V. Sindhwani, and B. Ramabhadran. “Kernel methods match Deep Neural Networks on TIMIT.” 2014 IEEE International Conference on Acoustics, Speech and Signal Processing. 2014, pp. 205–209.

バージョン履歴

R2022a で導入

R2023b: カーネル モデルで予測子の標準化をサポート

incrementalRegressionKernel で数値予測子の標準化がサポートされます。つまり、Standardize の値を true として指定することで、各数値予測子変数を対応する列の平均と標準偏差でセンタリングおよびスケーリングできます。ソフトウェアは、カテゴリカル予測子を標準化しません。

参考

incrementalLearner | fitrkernel | RegressionKernel

トピック

• インクリメンタル学習の概要
• インクリメンタル学習モデルの構成
• 簡潔なワークフローを使用した回帰用のインクリメンタル学習の実装
• 柔軟なワークフローを使用した回帰用のインクリメンタル学習の実装
• 回帰学習器で学習させた SVM 回帰モデルからのインクリメンタル学習モデルの初期化