コピュラ: 相関のある標本の生成
"コピュラ" は、変数間の依存関係を記述する関数であり、相関がある多変量データをモデル化する分布を作成する方法を提供します。コピュラを使うと、一変量周辺分布を指定することにより多変量分布を作成し、次に、コピュラを選択し、変数間の相関構造を与えることができます。より高次元の分布と同様に、二変量の分布も可能です。
シミュレーション入力間の依存関係を決定
モンテカルロ シミュレーションの設計で決めることの 1 つは、乱数入力に対する確率分布の選択です。それぞれの個体変数に分布を選択することは、多くの場合簡単です。ただし、入力の間にどのような依存関係があるかを判断するのは、難しい可能性があります。理想的には、シミュレーションへの入力データは、モデル化しようとする実際の量間の依存関係について既知であることを、反映しなければなりません。ただし、シミュレーションにおいて任意の依存関係について基にするべき情報がほとんどなかったり、あるいはまったくないことがあります。そのような場合、モデルの感度を判断するために、さまざまな可能性を試すことが有効です。
分布が標準多変量分布ではない場合、依存関係をもつ乱数入力の作成が難しくなることがあります。さらに、標準多変量分布のいくつかでは、依存関係に制限のあるタイプに限りモデル化できます。入力を独立にすることは、常に可能であり容易な選択ですが必ずしも目的にかなったものではなく、誤った結論を導く可能性があります。
たとえば、財務リスクのモンテカルロ シミュレーションでは、保険損失のさまざまな原因を表す 2 つの乱数入力を使用できます。これらの入力を対数正規分布の確率変数としてモデル化することがあります。当然疑問となるのは、これら 2 つの入力間の依存関係がシミュレーションの結果にどのように影響するかということです。事実、無作為な同一の条件が両方の原因に影響することが、実際のデータから理解できる場合もあります。シミュレーションでこれを無視すると、誤った結論が導かれる可能性があります。
正規確率変数の生成と累乗
関数 lognrnd は、対数正規分布に従う独立した確率変数をシミュレートします。以下の例で、関数 mvnrnd は、n 個のペアの独立した正規確率変数を生成してから、それらを累乗します。ここで、使われている共分散行列は対角形であることに注意してください。
n = 1000; sigma = .5; SigmaInd = sigma.^2 .* [1 0; 0 1]
SigmaInd = 2×2
0.2500 0
0 0.2500
rng('default'); % For reproducibility ZInd = mvnrnd([0 0],SigmaInd,n); XInd = exp(ZInd); plot(XInd(:,1),XInd(:,2),'.') axis([0 5 0 5]) axis equal xlabel('X1') ylabel('X2')

相関がある二変量対数正規確率変数は、非ゼロの非対角項をもつ共分散行列を使って、生成することも容易です。
rho = .7; SigmaDep = sigma.^2 .* [1 rho; rho 1]
SigmaDep = 2×2
0.2500 0.1750
0.1750 0.2500
ZDep = mvnrnd([0 0],SigmaDep,n); XDep = exp(ZDep);
さらに散布図を表示することで、これら 2 つの二変量分布間の違いがわかります。
plot(XDep(:,1),XDep(:,2),'.') axis([0 5 0 5]) axis equal xlabel('X1') ylabel('X2')
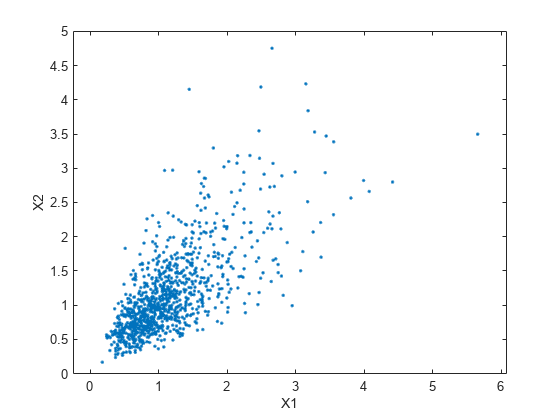
2 番目のデータ セットで、X1 の大きな値と X2 の大きな値に相関の傾向があり、また小さな値についても同様であることが明らかです。基となる二変量正規分布の相関パラメーター により、この依存性が決定されます。シミュレーションから導き出された結論は、従属関係をもつ X1 と X2 を生成したかどうかでかなり異なります。この場合、二変量対数正規分布を利用することができます。周辺分布が異なる対数正規分布である場合は、より高次元に容易に一般化されます。
多変量分布はこの他にもあります。たとえば、多変量 t 分布とディリクレ分布はそれぞれ、依存性のある t 確率変数とベータ確率変数をシミュレートします。しかし、簡単な多変量分布は多くはなく、境界がすべて同じ族になる (あるいは、厳密に同じ分布にもなる) 場合に、適用が限られます。これは、多くの状況で大きな制限となることがあります。
依存する二変量分布の作成
前の節の説明では、簡単な二変量対数正規分布を作成しましたが、これは、より一般に適用できる方法を説明するのに役立ちます。
二変量正規分布からの値のペアを生成します。これら 2 変量には、統計的な依存関係があり、それぞれは、正規周辺分布をもちます。
周辺分布を対数正規分布に変更して、それぞれの変数に変換 (指数関数) を別々に適用します。変換された変数には、やはり統計的な依存関係があります。
適切な変換が見つかれば、この方法は一般化されて、他の周辺分布をもつ、二変量の従属しているランダムなベクトルを作成できます。実際、累乗法のみを使う場合程簡単ではありませんが、そのような変換を作成する一般的な方法があります。
定義では、ここで Φ と示される正規累積分布関数 (cdf) を、標準の正規確率変数に適用すると、区間 [0, 1] 上で一様である確率変数になります。これは、Z が標準正規分布をもつ場合、U = Φ(Z) の累積分布関数が以下のようになることでわかります。
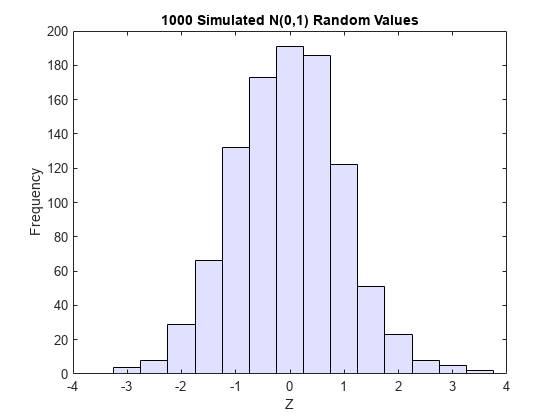
さらに、これは正規分布 (0,1) の確率変数の累積分布関数です。シミュレーションによって得られた正規分布と変換された値のヒストグラムは、以下の事実を示します。
n = 1000; rng default % for reproducibility z = normrnd(0,1,n,1); % generate standard normal data histogram(z,-3.75:.5:3.75,'FaceColor',[.8 .8 1]) % plot the histogram of data xlim([-4 4]) title('1000 Simulated N(0,1) Random Values') xlabel('Z') ylabel('Frequency')
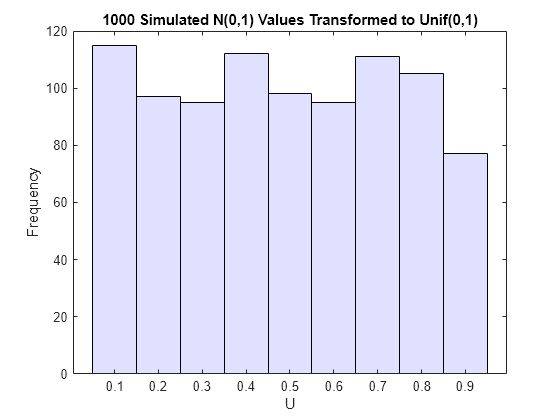
u = normcdf(z); % compute the cdf values of the sample data figure histogram(u,.05:.1:.95,'FaceColor',[.8 .8 1]) % plot the histogram of the cdf values title('1000 Simulated N(0,1) Values Transformed to Unif(0,1)') xlabel('U') ylabel('Frequency')
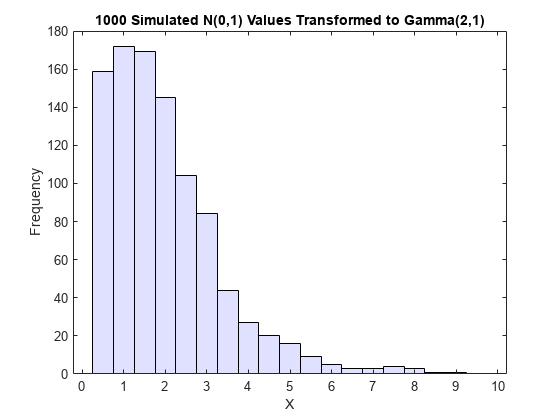
一変量の乱数発生の理論によると、正規分布(0,1) に従う確率変数に、任意の分布の累積分布逆関数 F を適用すると、正確に F 分布する確率変数になります (逆関数法を参照)。証明は、以前のケースに対する前述の証明とは本質的に逆になります。次のヒストグラムは、ガンマ分布への変換を示しています。
x = gaminv(u,2,1); % transform to gamma values figure histogram(x,.25:.5:9.75,'FaceColor',[.8 .8 1]) % plot the histogram of gamma values title('1000 Simulated N(0,1) Values Transformed to Gamma(2,1)') xlabel('X') ylabel('Frequency')
この 2 ステップの変換を二変量標準正規分布の各変数に適用して、任意の周辺分布をもつ独立でない確率変数を作成できます。変換は各成分に別々に作用するので、2 つの結果の確率変数は同じ周辺分布にはなりません。変換は、次の式で定義されます。
ここで、 と は、異なる 2 つの分布になる可能性のある逆 cdf です。たとえば、以下は 分布と Gamma(2,1) 周辺分布をもつ二変量分布から無作為なベクトルを生成します。
n = 1000; rho = .7; Z = mvnrnd([0 0],[1 rho; rho 1],n); U = normcdf(Z); X = [gaminv(U(:,1),2,1) tinv(U(:,2),5)]; % draw the scatter plot of data with histograms figure scatterhist(X(:,1),X(:,2),'Direction','out')
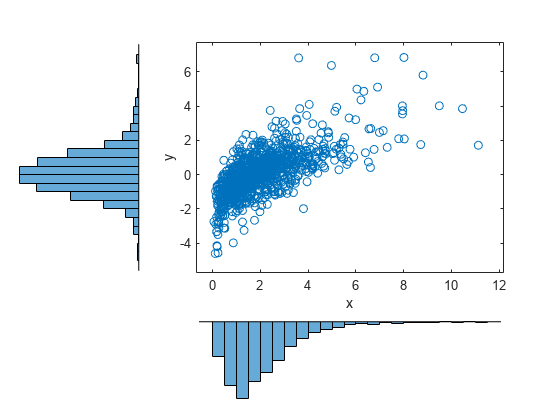
このプロットは、周辺分布と依存関係の両方を示すために、散布図と同時にヒストグラムも示します。
順位相関係数の使用
元になる二変量正規分布の相関パラメーター ρ は、この構造の X1 と X2 間の依存を決定します。しかし、X1 と X2 の線形相関は ρ ではありません。たとえば、オリジナルの対数正規分布の場合、その相関の閉形式は次のようになります。
これは ρ がちょうど 1 ではない限り、厳密に ρ より小さくなります。より一般的な場合 (ガンマ/t 構造など)、X1 と X2 の線形相関を ρ で表現することは困難または不可能ですが、同じ効果が起こることがシミュレーションで示されています。
これは、線形相関係数は確率変数間の線形の依存関係を表すためであり、非線形変換がこれらの確率変数に適用されるときに、線形相関は保存されません。代わりに、ケンドールの τ またはスピアマンの などの順位相関係数の方が適切です。
概略を説明すると、これらの順位相関は、他の大きい値 (または小さい値) に関連する 1 つの確率変数の大きい値 (または小さい値) に対して、順位を測定します。しかし、線形相関係数とは違い、これらは、順位についての関連のみを測ります。その結果、順位相関は単調な変換では保存されます。特に、前述の transformation 法は、順位相関を保存します。したがって、二変量の正規分布 Z の順位相関を正確に知れば、変換された最終の確率変数 X の順位相関が決まります。線形相関係数 ρ は、基になっている二変量正規分布をパラメーター表現するために必要になりますが、ケンドールの τ またはスピアマンの の方が、確率変数の依存関係を説明する際により効果的です。なぜなら、これらは周辺分布の選択に依存しないからです。
二変量正規分布の場合、ケンドールの τ またはスピアマンの と線形相関係数 ρ には次の簡単な 1 対 1 写像があります。
次のプロットは、この関係を示します。
rho = -1:.01:1; tau = 2.*asin(rho)./pi; rho_s = 6.*asin(rho./2)./pi; plot(rho,tau,'b-','LineWidth',2) hold on plot(rho,rho_s,'g-','LineWidth',2) plot([-1 1],[-1 1],'k:','LineWidth',2) axis([-1 1 -1 1]) xlabel('rho') ylabel('Rank correlation coefficient') legend('Kendall''s {\it\tau}', ... 'Spearman''s {\it\rho_s}', ... 'location','NW')
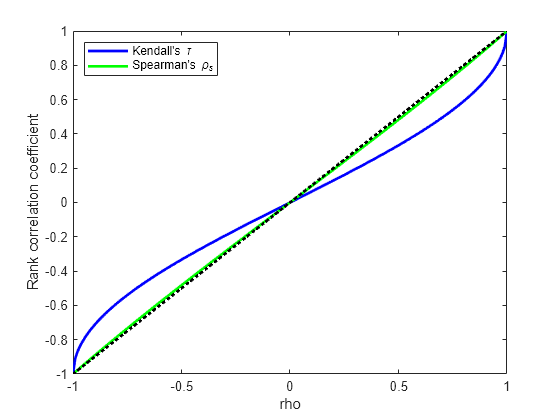
したがって、Z1 と Z2 の線形相関に正しい ρ パラメーター値を選択すると、X1 と X2 の間に、それらの周辺分布に関係なく、望ましい順位相関を容易に作成できます。
多変量正規分布の場合、スピアマンの順位相関は線形相関とほとんど同じです。しかし、最後に確率変数に変換すると、このことは成り立ちません。
二変量コピュラの使用
前の節で説明された最初のステップでは、二変量ガウス型コピュラとして知られるものを定義しています。コピュラとは、多変量の確率分布であり、各確率変数は、単位区間 [0,1] 上に一様な周辺分布をもちます。これらの変数は、完全に独立であるか、確定的に関連 (例: U2 = U1)、あるいはこれらの中間的なものです。変数間の依存関係の可能性のために、コピュラを使用して、依存する変数に対する新しい多変量分布を作成できます。おそらくさまざまな累積分布関数を使って、逆関数法でコピュラの各変数を別々に変換することによって、結果の分布は、任意の周辺分布をもつことができます。このような多変量分布は、異なるランダムな入力が互いに独立ではないことが既知である場合、シミュレーションでしばしば有効です。
Statistics and Machine Learning Toolbox™ 関数は以下を計算します。
線形相関からの順位相関 (
copulastat) と順位相関からの線形相関 (copulaparam)ランダムなベクトル (
copularnd)データに当てはめるコピュラのパラメーター (
copulafit)
たとえば、さまざまな依存構造の範囲を説明するために、関数 copularnd を使用して、さまざまなレベルの ρ に対して、二変量ガウス型コピュラからランダムな値の散布図を作成します。二変量ガウス型コピュラの族は、線形相関行列によってパラメーター表現されます。
U1 と U2 は、ρ が ±1 に近づくと線形依存に近づき、ρ がゼロに近づくと完全な独立に近づきます。
n = 500; rng('default') % for reproducibility U = copularnd('Gaussian',[1 .8; .8 1],n); subplot(2,2,1) plot(U(:,1),U(:,2),'.') title('{\it\rho} = 0.8') xlabel('U1') ylabel('U2') U = copularnd('Gaussian',[1 .1; .1 1],n); subplot(2,2,2) plot(U(:,1),U(:,2),'.') title('{\it\rho} = 0.1') xlabel('U1') ylabel('U2') U = copularnd('Gaussian',[1 -.1; -.1 1],n); subplot(2,2,3) plot(U(:,1),U(:,2),'.') title('{\it\rho} = -0.1') xlabel('U1') ylabel('U2') U = copularnd('Gaussian',[1 -.8; -.8 1],n); subplot(2,2,4) plot(U(:,1),U(:,2),'.') title('{\it\rho} = -0.8') xlabel('U1') ylabel('U2')
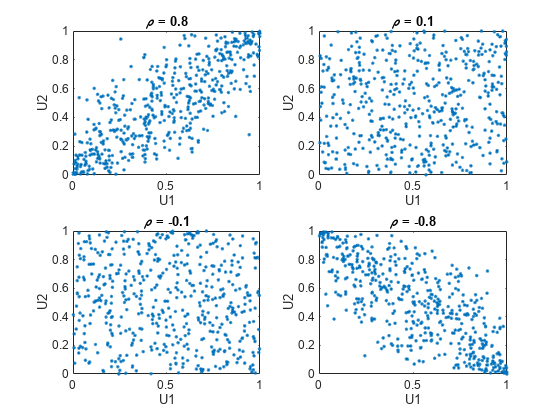
U1 と U2 の間の依存関係は、X1 = G(U1) と X2 = G(U2) の周辺分布からは完全に独立しています。X1 と X2 には任意の周辺分布を与えることができますが、順位相関は同じままです。これは、コピュラの主な利点の 1 つです。依存関係と周辺分布をこのように別々に特定することが可能になります。コピュラに対して確率密度関数 (copulapdf) と累積分布関数 (copulacdf) を計算することもできます。たとえば、次のプロットは、ρ = .8 に対する pdf と cdf を示します。
u1 = linspace(1e-3,1-1e-3,50); u2 = linspace(1e-3,1-1e-3,50); [U1,U2] = meshgrid(u1,u2); Rho = [1 .8; .8 1]; f = copulapdf('t',[U1(:) U2(:)],Rho,5); f = reshape(f,size(U1)); figure surf(u1,u2,log(f),'FaceColor','interp','EdgeColor','none') view([-15,20]) xlabel('U1') ylabel('U2') zlabel('Probability Density')
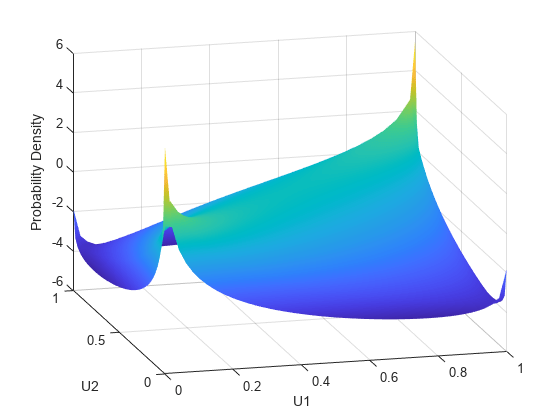
u1 = linspace(1e-3,1-1e-3,50); u2 = linspace(1e-3,1-1e-3,50); [U1,U2] = meshgrid(u1,u2); F = copulacdf('t',[U1(:) U2(:)],Rho,5); F = reshape(F,size(U1)); figure() surf(u1,u2,F,'FaceColor','interp','EdgeColor','none') view([-15,20]) xlabel('U1') ylabel('U2') zlabel('Cumulative Probability')
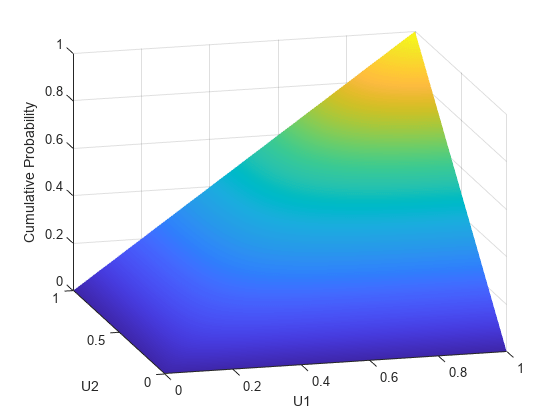
さまざまなコピュラ族は、二変量 t 分布から始め、対応する t 累積分布関数を使って変換することによって作成できます。二変量 t 分布は、線形相関行列 P と自由度 ν でパラメーター表現されます。こうして、たとえば、それぞれ自由度 1 と 5 をもつ多変量 t に基づき、 コピュラまたは コピュラを記述できます。
ガウス型コピュラの場合と同様に、Statistics and Machine Learning Toolbox の t コピュラの関数は、次のものを計算します。
線形相関からの順位相関 (
copulastat) と順位相関からの線形相関 (copulaparam)ランダムなベクトル (
copularnd)データに当てはめるコピュラのパラメーター (
copulafit)
たとえば、さまざまな依存構造の範囲を説明するために、関数 copularnd を使用して、さまざまなレベルの ρ に対して、二変量 コピュラからランダムな値の散布図を作成します。
n = 500; nu = 1; rng('default') % for reproducibility U = copularnd('t',[1 .8; .8 1],nu,n); subplot(2,2,1) plot(U(:,1),U(:,2),'.') title('{\it\rho} = 0.8') xlabel('U1') ylabel('U2') U = copularnd('t',[1 .1; .1 1],nu,n); subplot(2,2,2) plot(U(:,1),U(:,2),'.') title('{\it\rho} = 0.1') xlabel('U1') ylabel('U2') U = copularnd('t',[1 -.1; -.1 1],nu,n); subplot(2,2,3) plot(U(:,1),U(:,2),'.') title('{\it\rho} = -0.1') xlabel('U1') ylabel('U2') U = copularnd('t',[1 -.8; -.8 1],nu, n); subplot(2,2,4) plot(U(:,1),U(:,2),'.') title('{\it\rho} = -0.8') xlabel('U1') ylabel('U2')

t コピュラは、U1 と U2 に対する一様な周辺分布をもちます。ガウス型コピュラも同様な分布になります。t コピュラの成分間の順位相関 τ または は、ガウス型コピュラの ρ とも同じ関数です。ただし、これらのプロットが示すように、 コピュラは、これらの成分が同じ順位相関をもつ場合でも、ガウス型コピュラとはかなり異なります。この違いは、それらの依存関係の構造にあります。予想どおり、自由度パラメーター が大きくなるにつれて、 コピュラは対応するガウス型コピュラに近づきます。
ガウス型コピュラと同様に、任意の周辺分布は t コピュラに適用できます。たとえば、自由度 1 の t コピュラを使用し、copularnd を使って、Gamma(2,1) と 周辺分布をもつ二変量分布から、ランダムなベクトルを再び生成できます。
n = 1000; rho = .7; nu = 1; rng('default') % for reproducibility U = copularnd('t',[1 rho; rho 1],nu,n); X = [gaminv(U(:,1),2,1) tinv(U(:,2),5)]; figure scatterhist(X(:,1),X(:,2),'Direction','out')
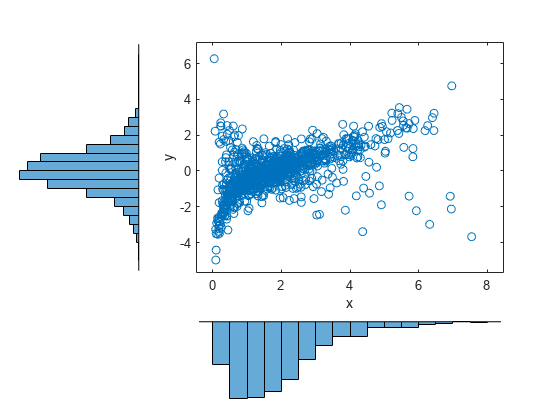
ガウス型コピュラに基づき以前に作成された二変量のガンマ/t 分布と比較して、 コピュラに基づきここで作成された分布は、周辺分布が同じで変数間の順位相関も同じですが、非常に異なる依存構造をもちます。これは、多変量分布は、周辺分布またはそれらの相関によって一意に定義されないということを示しています。アプリケーションで特定のコピュラの選択は、実際の観測されるデータに基づくことがあります。あるいは、入力の分布に対するシミュレーションの結果の感度を決める方法として、別のコピュラが使用されることもあります。
より高次元のコピュラ
ガウス型コピュラと t コピュラは、楕円コピュラとして知られています。楕円コピュラをより高次元に一般化することは容易です。たとえば、以下のように、ガウス型コピュラとcopularndを使用して、Gamma(2,1)、Beta(2,2)、 周辺分布をもつ三変量分布からのデータをシミュレートします。
n = 1000; Rho = [1 .4 .2; .4 1 -.8; .2 -.8 1]; rng('default') % for reproducibility U = copularnd('Gaussian',Rho,n); X = [gaminv(U(:,1),2,1) betainv(U(:,2),2,2) tinv(U(:,3),5)];
データをプロットする。
subplot(1,1,1) plot3(X(:,1),X(:,2),X(:,3),'.') grid on view([-55, 15]) xlabel('X1') ylabel('X2') zlabel('X3')
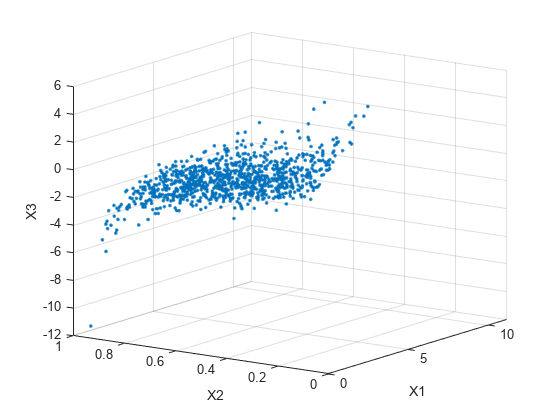
線形相関パラメーター ρ と、たとえば、ケンドールの τ の相関は、ここで使用される相関行列 P の各要素に対して成り立つことに注意してください。データの標本順位相関は、理論的な値にほぼ等しいことを確かめられます。
tauTheoretical = 2.*asin(Rho)./pi
tauTheoretical = 3×3
1.0000 0.2620 0.1282
0.2620 1.0000 -0.5903
0.1282 -0.5903 1.0000
tauSample = corr(X,'type','Kendall')
tauSample = 3×3
1.0000 0.2581 0.1414
0.2581 1.0000 -0.5790
0.1414 -0.5790 1.0000
アルキメデス型コピュラ
Statistics and Machine Learning Toolbox™ 関数は、次の 3 つの二変量アルキメデス型コピュラ族もサポートします。
Clayton (クレイトン) コピュラ
Frank (フランク)・コピュラ
Gumbel (ガンベル)・コピュラ
これらは、標準多変量分布を使って構成的に定義されているのではなく、それらの cdf で直接定義される 1 パラメーター族です。
これら 3 つのアルキメデス型コピュラをガウス型コピュラや t 二変量コピュラと比較するには、0.8 の線形相関パラメーターをもつガウス型コピュラまたは t コピュラに対して、最初に関数copulastatを使って順位相関を見つけてから、関数copulaparamを使って、その順位相関に対応するクレイトン コピュラ パラメーターを見つけます。
tau = copulastat('Gaussian',.8 ,'type','kendall')
tau = 0.5903
alpha = copulaparam('Clayton',tau,'type','kendall')
alpha = 2.8820
最後に、copularndを使って、クレイトン コピュラからの無作為標本をプロットします。Frank (フランク)・コピュラ、Gumbel (ガンベル)・コピュラに対して、同じ手順を繰り返します。
n = 500; U = copularnd('Clayton',alpha,n); subplot(3,1,1) plot(U(:,1),U(:,2),'.'); title(['Clayton Copula, {\it\alpha} = ',sprintf('%0.2f',alpha)]) xlabel('U1') ylabel('U2') alpha = copulaparam('Frank',tau,'type','kendall'); U = copularnd('Frank',alpha,n); subplot(3,1,2) plot(U(:,1),U(:,2),'.') title(['Frank Copula, {\it\alpha} = ',sprintf('%0.2f',alpha)]) xlabel('U1') ylabel('U2') alpha = copulaparam('Gumbel',tau,'type','kendall'); U = copularnd('Gumbel',alpha,n); subplot(3,1,3) plot(U(:,1),U(:,2),'.') title(['Gumbel Copula, {\it\alpha} = ',sprintf('%0.2f',alpha)]) xlabel('U1') ylabel('U2')
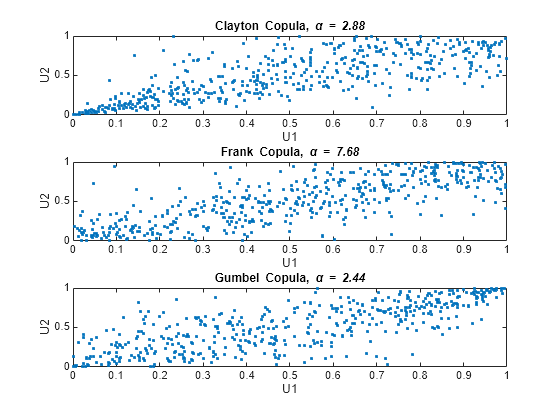
コピュラを使った従属多変量データのシミュレート
コピュラを使って従属している多変量データをシミュレートするには、以下の項目を指定しなければなりません。
コピュラ族 (と任意の形状パラメーター)
変数間の順位相関
各変数に対する周辺分布
2 つの株式に対するデータを返して、データと同じ分布に従う入力を使ってモンテカルロ シミュレーションを実行するとします。
load stockreturns nobs = size(stocks,1); subplot(2,1,1) histogram(stocks(:,1),10,'FaceColor',[.8 .8 1]) xlim([-3.5 3.5]) xlabel('X1') ylabel('Frequency') subplot(2,1,2) histogram(stocks(:,2),10,'FaceColor',[.8 .8 1]) xlim([-3.5 3.5]) xlabel('X2') ylabel('Frequency')

各データセットを別々にパラメトリック モデルで当てはめることができ、それらの推定を周辺分布として使用できます。しかし、パラメトリック モデルは、十分に適応性がないことがあります。代わりに、ノンパラメトリックなモデルを使用して、周辺分布に変換できます。ノンパラメトリック モデルに対しては、累積分布逆関数を計算する方法のみが必要になります。
関数ecdfで計算されるように、最も簡単なノンパラメトリックなモデルは経験累積分布関数です。離散的な周辺分布の場合、これは適切です。しかし、連続分布の場合、ecdf で計算されるステップ関数よりも滑らかなモデルを使用します。それを行う 1 つの方法は、経験累積分布関数を推定し、区分的な線形関数を使ってステップの中点間を内挿することです。別の方法は、ksdensityを使って、カーネル平滑化を使用することです。たとえば、最初の変数について、カーネル平滑化された累積分布関数の推定を、経験累積分布関数と比較します。
[Fi,xi] = ecdf(stocks(:,1)); figure() stairs(xi,Fi,'b','LineWidth',2) hold on Fi_sm = ksdensity(stocks(:,1),xi,'function','cdf','width',.15); plot(xi,Fi_sm,'r-','LineWidth',1.5) xlabel('X1') ylabel('Cumulative Probability') legend('Empirical','Smoothed','Location','NW') grid on
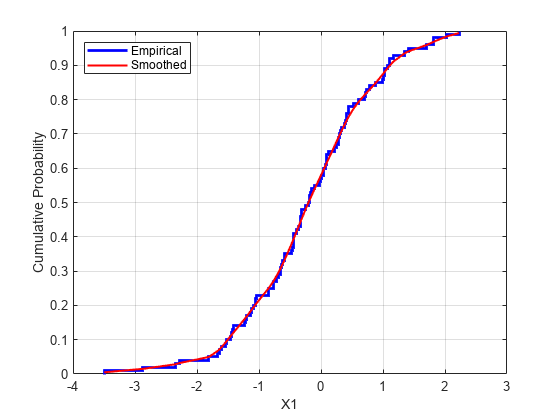
別のコピュラと相関を試み、シミュレートします。ここでは、かなり小さい自由度パラメーターをもつ二変量 t コピュラを使用します。相関パラメーターに対し、データの順位相関を計算することができます。
nu = 5; tau = corr(stocks(:,1),stocks(:,2),'type','kendall')
tau = 0.5180
copulaparamを使用して、t コピュラの対応する線形相関パラメーターを見つけます。
rho = copulaparam('t', tau, nu, 'type','kendall')
rho = 0.7268
次に、copularndを使用して、t コピュラからランダムな値を生成し、ノンパラメトリックな逆 cdf を使って変換します。関数ksdensityにより、分布のカーネル推定を作成し、次の 1 ステップでコピュラ点での累積分布逆関数を評価できます。
n = 1000; U = copularnd('t',[1 rho; rho 1],nu,n); X1 = ksdensity(stocks(:,1),U(:,1),... 'function','icdf','width',.15); X2 = ksdensity(stocks(:,2),U(:,2),... 'function','icdf','width',.15);
あるいは、多くのデータをもっていたり、2 つ以上の値のセットをシミュレートしなければならない場合、累積分布逆関数を、区間 (0,1) の格子点で計算したり、コピュラ点で評価する内挿を使用すると、より効率的です。
p = linspace(0.00001,0.99999,1000); G1 = ksdensity(stocks(:,1),p,'function','icdf','width',0.15); X1 = interp1(p,G1,U(:,1),'spline'); G2 = ksdensity(stocks(:,2),p,'function','icdf','width',0.15); X2 = interp1(p,G2,U(:,2),'spline'); scatterhist(X1,X2,'Direction','out')
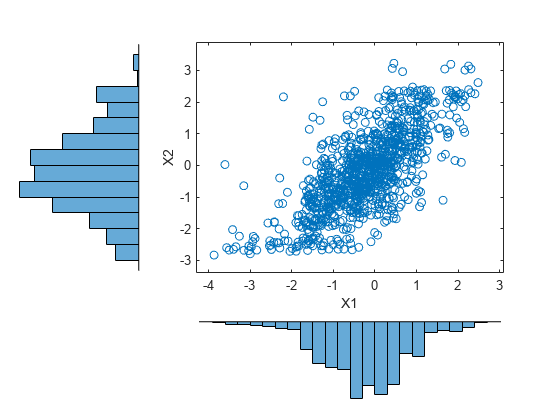
シミュレートされたデータの周辺ヒストグラムは、オリジナルのデータに対するヒストグラムを平滑化したものです。平滑化量は、ksdensityへのバンド幅の入力で制御されています。
コピュラのデータへの当てはめ
この例では、copulafit を使用してデータのコピュラを測定する方法を示します。行列 X のデータの分布のような (周辺分布と相関の点で) 分布のデータ Xsim を生成するには、周辺分布を X の列に近似し、適切な累積分布関数を使用して X を U に変換して U が 0 から 1 の範囲の値になるようにし、copulafit を使用してコピュラを U に近似し、コピュラから新規データ Usim を生成し、適切な逆累積分布関数を使用して Usim を Xsim に変換する必要があります。
シミュレートされた株式収益データを読み込み、プロットします。
load stockreturns x = stocks(:,1); y = stocks(:,2); scatterhist(x,y,'Direction','out')

累積分布関数のカーネル推定器を使って、データをコピュラ スケール (単位正方形) に変換します。
u = ksdensity(x,x,'function','cdf'); v = ksdensity(y,y,'function','cdf'); scatterhist(u,v,'Direction','out') xlabel('u') ylabel('v')
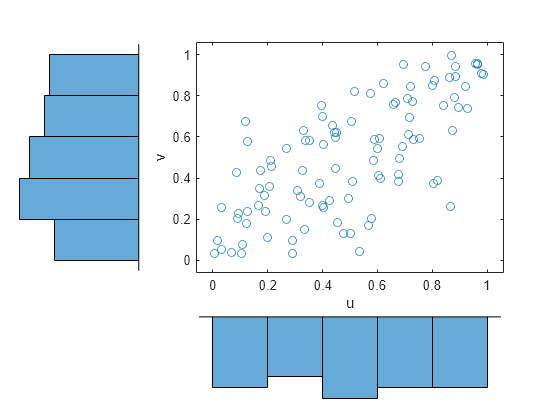
t コピュラを当てはめます。
[Rho,nu] = copulafit('t',[u v],'Method','ApproximateML')
Rho = 2×2
1.0000 0.7220
0.7220 1.0000
nu = 2.6133e+06
t コピュラから無作為標本を生成します。
r = copularnd('t',Rho,nu,1000); u1 = r(:,1); v1 = r(:,2); scatterhist(u1,v1,'Direction','out') xlabel('u') ylabel('v') set(get(gca,'children'),'marker','.')
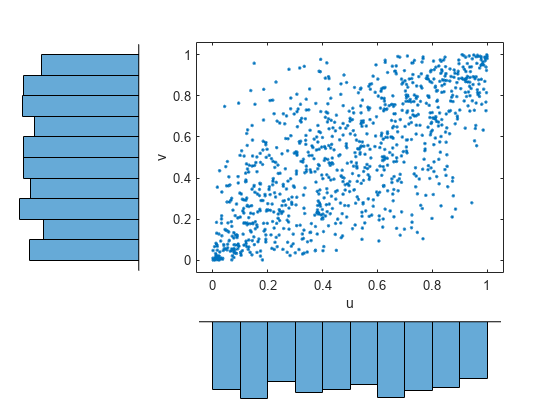
無作為標本を変換して、データのオリジナルのスケールに戻します。
x1 = ksdensity(x,u1,'function','icdf'); y1 = ksdensity(y,v1,'function','icdf'); scatterhist(x1,y1,'Direction','out') set(get(gca,'children'),'marker','.')
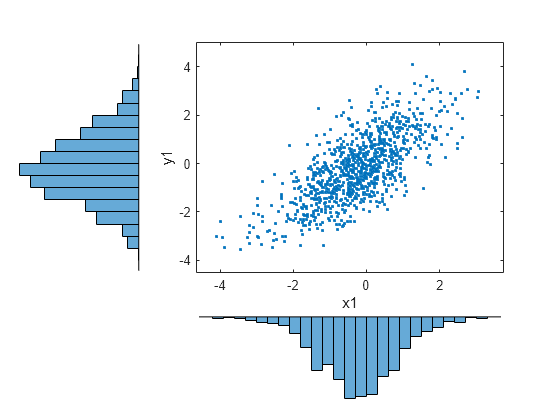
例が示すように、コピュラは他の分布近似関数と自然に統合されます。
参考
copulacdf | copulafit | copulaparam | copulapdf | copulastat | copularnd