疑似乱数の生成

"疑似乱数" は決定性アルゴリズムによって生成されます。準乱数は分布と相関関係で統計的検定に合格しており、その点では "乱数" といえます。ランダムなプロセスではなく、アルゴリズムによって生成される点では真の乱数と異なります。

MATLAB^® などの "乱数発生器" (RNG) は、指定された分布によって疑似乱数を生成するアルゴリズムです。

サポートされる分布の乱数発生用の GUI の詳細は、乱数発生 UI の調査を参照してください。

より複雑な確率分布には、マルコフ連鎖サンプラーを使用する標本分布の表現で説明されている方法を使用できます。

一般的な疑似乱数発生法

• 直接法

• 逆関数法

• 棄却採択法

疑似乱数を生成するためのメソッドは、MATLAB の関数 rand が生成するように、通常、一様乱数で始まります。この節で紹介するメソッドは、どのように乱数を他の分布から生成するかを詳しく説明します。

直接法

直接法は、分布の定義を直接利用します。

たとえば、二項分布乱数について考えてみましょう。二項分布の乱数は、コインを投げたときに表が出る確率が $$p$$ であるコインを $$N$$ 回投げたときに表が出る回数です。範囲 (0,1) の一様乱数を $$N$$ 個生成して $$p$$ より小さい数をカウントした場合、カウントは $$N$$ および $$p$$ というパラメーターをもつ二項分布乱数になります。

この関数は、この方法を使った、二項分布に従う乱数発生の簡単な例です。

function X = directbinornd(N,p,m,n)
    X = zeros(m,n); % Preallocate memory
    for i = 1:m*n
        u = rand(N,1);
        X(i) = sum(u < p);
    end
end

以下に例を示します。

rng('default') % For reproducibility
X = directbinornd(100,0.3,1e4,1);
histogram(X,101)

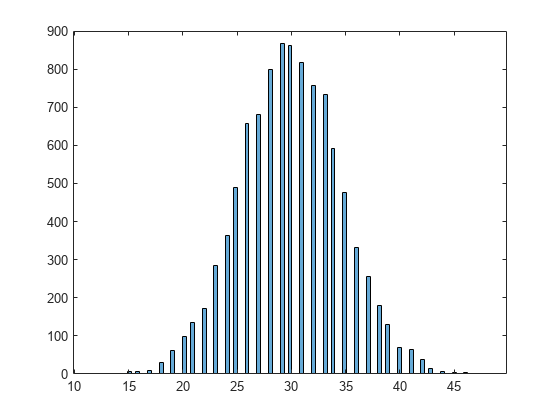
関数 binornd は、ベルヌーイ確率変数の総和という二項確率変数の定義に基づいて、修正された直接法を使用します。

上記の方法は、パラメーター $$\lambda$$ をもつポアソン分布用の乱数発生器に容易に変更することができます。ポアソン分布は、$$Np$$ を $$\lambda$$ に固定して $$N$$ を無限大に、$$p$$ をゼロに近づけたときの二項分布の極限のケースです。ポアソン乱数を生成するには、前述の乱数発生器の入力を $$N$$ と $$p$$ ではなく $$\lambda$$ に設定し、内部で $$N$$ を大きい値に、$$p$$ を $$\lambda /N$$ に設定します。

関数 poissrnd は、実際には 2 つの直接法を使用します。

• $$\lambda$$ の値が小さい場合は待ち時間法

• $$\lambda$$ の値が大きい場合は Ahrens と Dieter による方法

逆関数法

逆関数法は、連続的な累積分布関数 (cdf) が区間 (0,1) で一様に分布する観測値に基づきます。$$u$$ が (0,1) 内の一様乱数である場合、$$X=F^{-1}(U)$$ を使用して、cdf として $$F$$ が指定された連続分布から乱数 $$X$$ が生成されます。

たとえば、次のコードは、累積分布逆関数と MATLAB® の一様乱数発生器randを使用して、特定の指数分布から乱数を生成します。

rng('default') % For reproducibility
mu = 1;
X = expinv(rand(1e4,1),mu);

生成された乱数の分布と指定の指数の pdf を比較します。

numbins = 50;
h = histogram(X,numbins,'Normalization','pdf');
hold on
x = linspace(h.BinEdges(1),h.BinEdges(end));
y = exppdf(x,mu);
plot(x,y,'LineWidth',2)
hold off

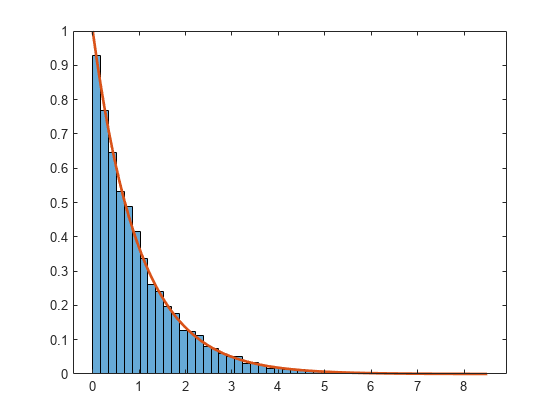
また、逆関数法を離散分布にも使用できます。確率質量ベクトル $$P(X=x_i)=p_i$$ ($$x_0<x_1<x_2<...$$) をもつ離散分布から乱数 $$X$$ を生成するには、(0,1) で一様乱数 $$u$$ を生成してから、$$F(x_{i-1})<u<F(x_i)$$ である場合に $$X=x_i$$ を設定します。

たとえば、次の関数は確率質量ベクトル $$p$$ をもつ離散分布について逆関数法を実装します。

function X = discreteinvrnd(p,m,n)
    X = zeros(m,n); % Preallocate memory
    for i = 1:m*n
        u = rand;
        I = find(u < cumsum(p));
        X(i) = min(I);
    end
end

この関数を使用して、任意の離散分布から乱数を生成します。

p = [0.1 0.2 0.3 0.2 0.1 0.1]; % Probability mass function (pmf) values
X = discreteinvrnd(p,1e4,1);

代わりに、関数discretizeを使用して離散乱数を生成することもできます。

X = discretize(rand(1e4,1),[0 cusmsum(p)]);

生成された乱数のヒストグラムをプロットし、分布が指定の pmf 値に従うことを確認します。

histogram(categorical(X),'Normalization','probability')

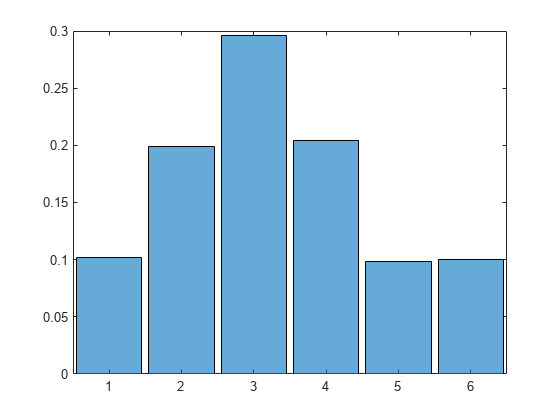
棄却採択法

分布の関数形によっては、直接法や逆関数法による乱数の発生は困難だったり、時間がかかってしまうものがあります。棄却採択法は、このような場合の代替法です。

棄却採択法は一様乱数で始めますが、さらに乱数発生器の利用が必要です。pdf が $$f$$ である連続分布から乱数を生成することが目的である場合、棄却採択法では、何らかの $$c$$ とすべての $$x$$ について $$f(x)\le cg(x)$$ を満たす $$g$$ という pdf をもつ連続分布から乱数を生成します。

連続の棄却採択法による乱数発生は、以下のように進めます。

1. 密度 $$g$$ を選択します。

2. すべての $$x$$ について $$f(x)/g(x)\le c$$ となる定数 $$c$$ を求めます。

3. 一様乱数 $$u$$ を生成します。

4. $$g$$ から乱数 $$v$$ を生成します。

5. $$cu\le f(v)/g(v)$$ である場合、$$v$$ を採択して返します。それ以外の場合は、$$v$$ を棄却して手順 3 に進みます。

効率を向上させるには、$$g$$ から乱数を生成する「簡単」な方法が必要であり、スカラー $$c$$ を小さくするべきです。単一の乱数を生成する反復回数の期待値は $$c$$ です。

次の関数は、与えられた $$f$$、$$g$$、$$g$$ の乱数発生器 grnd、および定数 $$c$$ に対して、棄却採択法を実施して確率密度関数 $$f$$ から乱数を生成します。

function X = accrejrnd(f,g,grnd,c,m,n)
    X = zeros(m,n); % Preallocate memory
    for i = 1:m*n
        accept = false;
        while accept == false
            u = rand();
            v = grnd();
            if c*u <= f(v)/g(v)
               X(i) = v;
               accept = true;
            end
        end
    end
end

たとえば、関数 $$f(x)=x{e}^{-x^2/2}$$ は、pdf の条件 (非負かつ積分すると 1) を $$[0,\infty )$$ で満たしています。平均が 1 である指数 pdf、 $$f(x)=e^{-x}$$ は、$$c$$ がおよそ 2.2 を上回る場合に $$g$$ を決定づけています。したがって、randとexprndを使用して $$f$$ から乱数を生成できます。

f = @(x)x.*exp(-(x.^2)/2);
g = @(x)exp(-x);
grnd = @()exprnd(1);
rng('default') % For reproducibility
X = accrejrnd(f,g,grnd,2.2,1e4,1);

確率密度関数 $$f$$ は、実際には形状パラメーターが 1 のレイリー分布です。この例では、棄却採択法で生成される乱数の分布をraylrndで生成されるものと比較します。

Y = raylrnd(1,1e4,1); 
histogram(X)
hold on
histogram(Y)
legend('A-R RNG','Rayleigh RNG')

関数 raylrnd は、変換法を使用して、randnによって計算されるカイ二乗確率変数に関してレイリー確率変数を表します。

また、棄却採択法を離散分布にも使用できます。この場合の目的は、確率質量が $$P_q(X=i)=q_i$$ である分布から乱数を生成する方法があると仮定した場合に、確率質量が $$P_p(X=i)=p_i$$ である分布から乱数を生成することです。乱数発生器は、次のように進めます。

1. 密度 $$P_q$$ を選択します。

2. すべての $$i$$ について $$p_i/q_i\le c$$ となる定数 $$c$$ を求めます。

3. 一様乱数 $$u$$ を生成します。

4. $$P_q$$ から乱数 $$v$$ を生成します。

5. $$cu\le p_v/q_v$$ である場合、$$v$$ を採択して返します。それ以外の場合は、$$v$$ を棄却して手順 3 に進みます。

関連するトピック

• 乱数発生
• 準乱数の生成
• 一様分布の逆関数を使用した乱数の生成
• マルコフ連鎖サンプラーを使用する標本分布の表現