準乱数の生成

準乱数列

準乱数発生器 (QRNG) は、単位超立方体のきわめて一様な標本を生成します。準乱数発生器は、超立方体の一様な分割のサブキューブごとに、生成された点の分布と点を均等に配置した分布の間の "不一致" を最小化します。その結果、準乱数発生器は、生成された準乱数列の初期セグメント内で体系的に "穴" を満たします。

一般的な疑似乱数発生法で説明した疑似乱数列とは異なり、準乱数列は多くのランダム統計検定に失敗します。しかし、真のランダムの近似はその目的ではありません。準乱数列は、初期のセグメントがこの行動を指定の密度まで近似させる方法により、均一に空間を満たします。

準乱数発生器の適用例としては、次のようなものがあります。

準モンテカルロ法 (QMC)。モンテカルロ法は、閉形式解なしで難しい多次元積分を評価するためにしばしば使用されます。準モンテカルロ法は準乱数列を使用して、この技術の収束プロパティを改善します。
空白を埋める実験計画。多くの実験設定において、すべての要因設定で測定を行うことは費用がかかり、不可能です。準乱数列は効率的で一様なサンプリングの設計空間を提供します。
グローバル最適化。最適化アルゴリズムは一般的に初期値の近傍でローカルな最適値を見つけます。初期値の準乱数列を使用することにより、グローバルな最適値検索は、すべてのローカルな最小の引き込み領域を一様にサンプリングします。

例: スクランブル、リープおよびスキップの使用

単純な 1 次元の数列で 1 ～ 10 の整数を生成するとします。この基本的な数列の最初の 3 つの点は [1,2,3] です。

それでは、Scramble、Skip、および Leap がどのように機能するかを見ていきましょう。

Scramble －スクランブルは、さまざまな方法のいずれかで点を入れ替えます。この例では、スクランブルによって、数列が 1,3,5,7,9,2,4,6,8,10 に変換されます。最初の 3 つの点は [1,3,5] になりました。
Skip － Skip 値は、無視する最初の点の数を指定します。この例では、Skip の値を 2 に設定します。数列は 5,7,9,2,4,6,8,10 になり、最初の 3 つの点は [5,7,9] になります。
Leap － Leap 値は、1 回ごとに無視する点の数を指定します。この例で Leap を 1 に、Skip を 2 に設定すると、数列の点は 1 つおきに使用されます。この例では、数列は 5,9,4,8 になり、最初の 3 つの点は [5,9,4] になります。

準乱数の点集合

Statistics and Machine Learning Toolbox™ 関数は、以下の準乱数列をサポートします。

ハルトン列。関数 haltonset によって生成されます。この列は、異なる主要ベースを使用して、ユニット間隔のより細かい一様な分割を次元ごとに連続して形成します。
ソボル列。関数 sobolset によって生成されます。この列は、2 の基底を使用して、ユニット間隔のより細かい一様な分割を連続して形成し、さらに、次元ごとに座標を並べ替えます。
ラテン超方格列。関数 lhsdesign によって生成されます。不一致を最小化するという意味では準乱数ではありませんが、この列は実験計画に役立つスパースな一様標本を生成します。

準乱数列は正の整数から単位超立方体までの関数です。応用で役立てるには、数列の初期 "点集合" を生成しなければなりません。点集合はサイズ n 行 d 列の行列です。ここで、n は点の数であり、d はサンプリングされている超立方体の次元です。関数 haltonset と sobolset は、指定の準乱数列のプロパティで点集合を構成します。点集合の初期セグメントは、haltonset クラスと sobolset クラスの net メソッドによって生成されます。ただし、かっこによるインデックス付けを使用すると、点の生成とアクセスをより一般的に行うことができます。

準乱数列を生成する方法が原因で、それらは、特に初期セグメントとより高次の次元内に不適当な相関関係を含む可能性があります。この問題に対処するため、多くの場合、準乱数の点集合では数列内の値を "スキップ"、"リープ" または "スクランブル" します。関数 haltonset および関数 sobolset を使用すると、準乱数列の Skip プロパティと Leap プロパティの両方を指定できます。また、haltonset クラスおよび sobolset クラスの scramble メソッドを使用すると、さまざまなスクランブル方法を適用できます。また、スクランブルは一様性を改良しながら、相関関係を減少します。

準乱数の点集合の生成

ライブスクリプトを開く

この例では、haltonset を使用して 2 次元 Halton 準乱数点集合を構築する方法を説明します。

haltonset オブジェクト p を作成し、シーケンスの最初の 1000 個の値をスキップし、101 番目ごとの点を保持します。

rng default  % For reproducibility
p = haltonset(2,'Skip',1e3,'Leap',1e2)

p = 
Halton point set in 2 dimensions (89180190640991 points)

Properties:
              Skip : 1000
              Leap : 100
    ScrambleMethod : none

オブジェクト p は指定の準乱数列のプロパティをカプセル化します。点集合は有限です。Skip および Leap プロパティと、点集合インデックスのサイズにおける限界により長さが決まります。

scramble を使用して、基数反転スクランブルを適用します。

p = scramble(p,'RR2')

p = 
Halton point set in 2 dimensions (89180190640991 points)

Properties:
              Skip : 1000
              Leap : 100
    ScrambleMethod : RR2

net を使用して、最初の 500 点を生成します。

X0 = net(p,500);

これは、以下の式と等価です。

X0 = p(1:500,:);

net またはかっこインデックスを使用して p にアクセスするまで、点集合 X0 の値はメモリ内で生成され、格納されません。

準乱数の本質を理解するために、X0 における 2 次元の散布図を作成します。

scatter(X0(:,1),X0(:,2),5,'r')
axis square
title('{\bf Quasi-Random Scatter}')

Figure contains an axes object. The axes object with title blank Quasi-Random blank Scatter contains an object of type scatter.

これを関数 rand が生成した一様な疑似乱数の散布と比較します。

X = rand(500,2);
scatter(X(:,1),X(:,2),5,'b')
axis square
title('{\bf Uniform Random Scatter}')

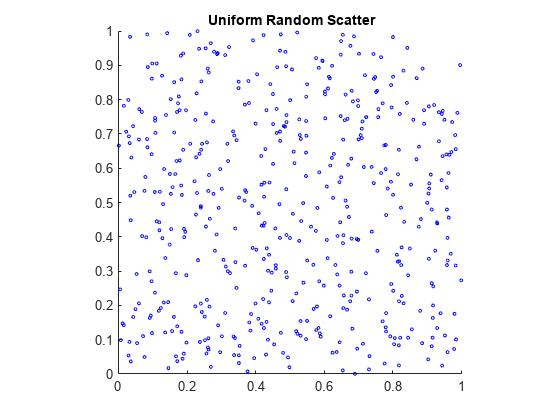
Figure contains an axes object. The axes object with title blank Uniform blank Random blank Scatter contains an object of type scatter.

準乱数の散布は、疑似乱数の散布が凝集しないため、より一様になります。

統計という意味では、準乱数は一様過ぎ、従来のランダムの検定には合格しません。たとえば、kstest で行うコルモゴロフ・スミルノフ検定は、点集合が一様でランダムな分布をもっているかどうかを検査するために使用されます。rand が生成したような一様な疑似無作為標本に対して繰り返し実行すると、検定は p 値の一様な分布を生成します。

nTests = 1e5;
sampSize = 50;
PVALS = zeros(nTests,1);
for test = 1:nTests
    x = rand(sampSize,1);
    [h,pval] = kstest(x,[x,x]);
    PVALS(test) = pval;
end

histogram(PVALS,100)
h = findobj(gca,'Type','patch');
xlabel('{\it p}-values')
ylabel('Number of Tests')

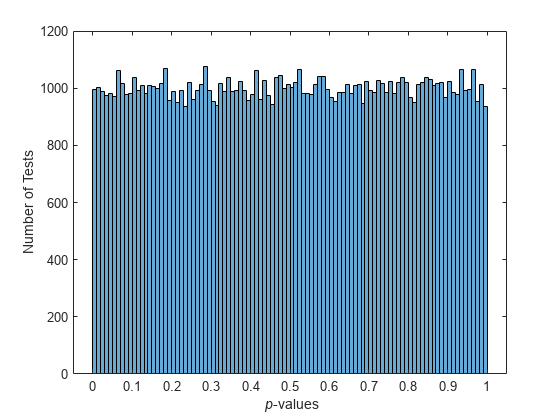
Figure contains an axes object. The axes object with xlabel blank p -values, ylabel Number of Tests contains an object of type histogram.

一様な準乱数標本に対して検定を繰り返し実行すると、結果はまったく異なります。

p = haltonset(1,'Skip',1e3,'Leap',1e2);
p = scramble(p,'RR2');

nTests = 1e5;
sampSize = 50;
PVALS = zeros(nTests,1);
for test = 1:nTests
    x = p(test:test+(sampSize-1),:);
    [h,pval] = kstest(x,[x,x]);
    PVALS(test) = pval;
end

histogram(PVALS,100)
xlabel('{\it p}-values')
ylabel('Number of Tests')

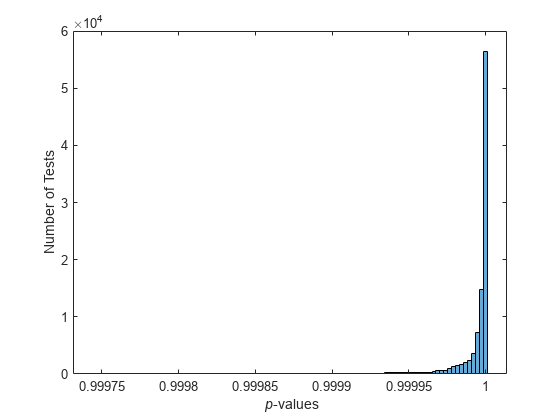
Figure contains an axes object. The axes object with xlabel blank p -values, ylabel Number of Tests contains an object of type histogram.

小さい p 値では、データが一様に分布される帰無仮説が疑わしくなります。仮説が真である場合は、p 値の約 5% が 0.05 を下回ることが予測されます。結果は明白に一貫しており、仮説に挑むのは無理です。

準乱数ストリーム

関数 qrandstream によって生成される準乱数の "ストリーム" は、特定のサイズの点集合ではなく、一連の準乱数出力を生成するために使用されます。クライアントの応用が間欠的にアクセスできる不定サイズの準乱数のソースを必要としている場合、ストリームは rand などの疑似乱数発生器と同じように使用されます。タイプ (ハルトンかソボル)、次元、skip、leap、scramble などの準乱数ストリームのプロパティは、ストリームが構成されるときに設定されます。

実行中、アクセスは異なりますが、準乱数ストリームは本質的に非常に大きな準乱数の点集合です。準乱数ストリームの "状態" は、次にストリームから取得する点のスカラーインデックスです。qrandstreamqrandstream クラスの qrand メソッドを使用して、現在の状態を起点とするストリームから点を生成します。reset メソッドを使用して、状態を 1 にリセットします。点集合とは異なり、ストリームはかっこインデックスをサポートしません。

準乱数ストリームの生成

ライブスクリプトを開く

この例では、準乱数の点集合から標本を生成する方法を示します。

haltonset を使用して準乱数点集合 p を作成し、繰り返し点集合 test にインデックスを増加し、異なる標本を生成します。

p = haltonset(1,'Skip',1e3,'Leap',1e2);
p = scramble(p,'RR2');

nTests = 1e5;
sampSize = 50;
PVALS = zeros(nTests,1);
for test = 1:nTests
    x = p(test:test+(sampSize-1),:);
    [h,pval] = kstest(x,[x,x]);
    PVALS(test) = pval;
end

qrandstream を使用して、点集合 p に基づく準乱数ストリーム q を構成し、ストリームがインデックスへの増加に対応するようにすることで、同じ結果が得られます。

p = haltonset(1,'Skip',1e3,'Leap',1e2);
p = scramble(p,'RR2');
q = qrandstream(p);

nTests = 1e5;
sampSize = 50;
PVALS = zeros(nTests,1);
for test = 1:nTests
    X = qrand(q,sampSize);
    [h,pval] = kstest(X,[X,X]);
    PVALS(test) = pval;
end