順位相関による相関データの生成

この例では、コピュラと順位相関を使用して、累積分布逆関数を使用できない確率分布 (ピアソンの柔軟な分布族など) から相関データを生成する方法を示します。

手順 1. ピアソン乱数を生成する。

関数pearsrndを使用して、2 つの異なるピアソン分布から 1000 個の乱数を生成します。1 番目の分布のパラメーター値は、mu が 0、sigma が 1、歪度が 1、尖度が 4 です。2 番目の分布のパラメーター値は、mu が 0、sigma が 1、歪度が 0.75、尖度が 3 です。

rng default  % For reproducibility
p1 = pearsrnd(0,1,-1,4,1000,1);
p2 = pearsrnd(0,1,0.75,3,1000,1);

この段階では、p1 と p2 はそれぞれのピアソン分布に由来する独立した標本であり、相関はありません。

手順 2. ピアソン乱数をプロットする。

scatterhistプロットを作成してピアソン乱数を可視化します。

figure
scatterhist(p1,p2)

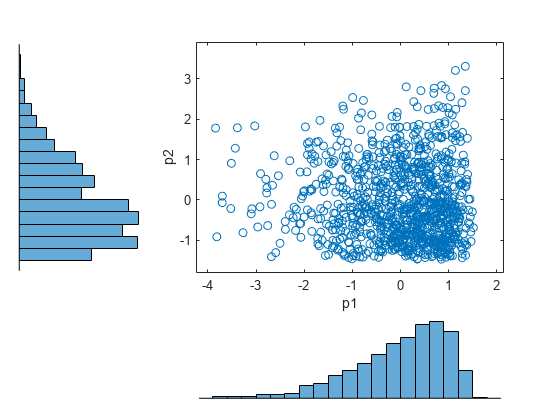
ヒストグラムは p1 と p2 の周辺分布を示しています。散布図は p1 と p2 の同時分布を示しています。散布図にパターンがないことから、p1 と p2 が独立していることがわかります。

手順 3. ガウス型コピュラを使用して乱数を生成する。

copularndでガウス型コピュラを使用して、相関係数が -0.8 の相関関係がある 1000 個の乱数を生成します。scatterhistプロットを作成して、コピュラから生成した乱数を可視化します。

u = copularnd('Gaussian',-0.8,1000);
figure
scatterhist(u(:,1),u(:,2))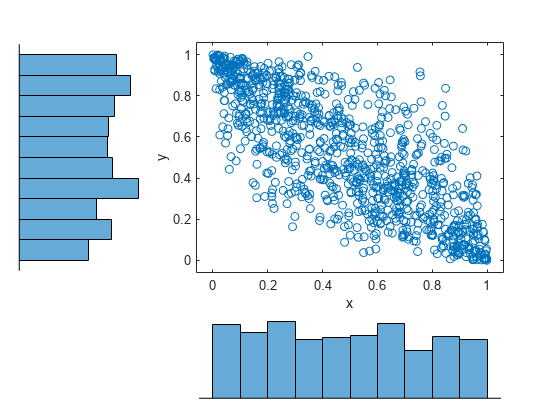

ヒストグラムは、コピュラの各列のデータに一様な周辺分布があることを示しています。散布図は、2 つの列のデータに負の相関があることを示しています。

手順 4. コピュラ乱数を並べ替える。

スピアマンの順位相関を使用して、2 つの独立したピアソン標本を相関データに変換します。

関数sortを使用して、コピュラ乱数を昇順で並べ替え、再編成した数値の順序を表すインデックスのベクトルを取得します。

[s1,i1] = sort(u(:,1));
[s2,i2] = sort(u(:,2));

s1 と s2 には、昇順で並べ替えたコピュラ u の 1 列目と 2 列目の数値が格納されます。i1 と i2 は、s1 と s2 の再編成された要素の順序を表すインデックス ベクトルです。たとえば、並べ替えたベクトル s1 の 1 番目の値が元のベクトルの 3 番目の値である場合、インデックス ベクトル i1 の 1 番目の値は 3 になります。

手順 5. スピアマンの順位相関を使用してピアソン標本を変換する。

並べ替えたコピュラ ベクトル s1 および s2 と同じサイズの、ゼロから構成される 2 つのベクトル x1 および x2 を作成します。p1 と p2 の値を昇順で並べ替えます。コピュラ乱数を並べ替えて生成したインデックス i1 および i2 と同じ順序で、x1 と x2 に値を設定します。

x1 = zeros(size(s1));
x2 = zeros(size(s2));

x1(i1) = sort(p1);
x2(i2) = sort(p2);

手順 6. 相関関係があるピアソン乱数をプロットする。

scatterhist プロットを作成して、相関関係があるピアソン データを可視化します。

figure
scatterhist(x1,x2)

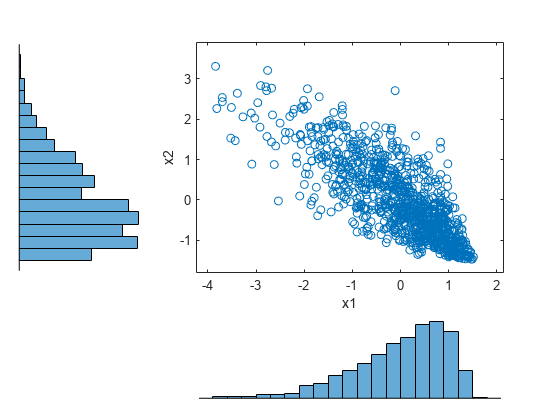
ヒストグラムは、データの各列の周辺ピアソン分布を示しています。散布図は、p1 と p2 の同時分布を示しています。データが負の相関関係であることがわかります。

手順 7. スピアマン順位相関係数の値を確認する。

相関関係があるピアソン乱数とコピュラ乱数でスピアマン順位相関係数が同じであることを確認します。

copula_corr = corr(u,'Type','spearman')

copula_corr = 2×2

    1.0000   -0.7858
   -0.7858    1.0000

pearson_corr = corr([x1,x2],'Type','spearman')

pearson_corr = 2×2

    1.0000   -0.7858
   -0.7858    1.0000

スピアマン順位相関は、コピュラ乱数とピアソン乱数で同じになっています。

参考

copularnd | corr | sort

関連するトピック

• コピュラ: 相関のある標本の生成