bayesopt
Select optimal machine learning hyperparameters using Bayesian optimization
Description
results = bayesopt(fun,vars)vars that minimize fun(vars).
Note
To include extra parameters in an objective function, see Parameterizing Functions.
results = bayesopt(fun,vars,Name,Value)Name,Value
arguments.
Examples
This example shows how to create a BayesianOptimization object by using bayesopt to minimize cross-validation loss.
Optimize hyperparameters of a KNN classifier for the ionosphere data, that is, find KNN hyperparameters that minimize the cross-validation loss. Have bayesopt minimize over the following hyperparameters:
Nearest-neighborhood sizes from 1 to 30
Distance functions
'chebychev','euclidean', and'minkowski'.
For reproducibility, set the random seed, set the partition, and set the AcquisitionFunctionName option to 'expected-improvement-plus'. To suppress iterative display, set 'Verbose' to 0. Pass the partition c and fitting data X and Y to the objective function fun by creating fun as an anonymous function that incorporates this data. See Parameterizing Functions.
load ionosphere rng default num = optimizableVariable('n',[1,30],'Type','integer'); dst = optimizableVariable('dst',{'chebychev','euclidean','minkowski'},'Type','categorical'); c = cvpartition(351,'Kfold',5); fun = @(x)kfoldLoss(fitcknn(X,Y,'CVPartition',c,'NumNeighbors',x.n,... 'Distance',char(x.dst),'NSMethod','exhaustive')); results = bayesopt(fun,[num,dst],'Verbose',0,... 'AcquisitionFunctionName','expected-improvement-plus')
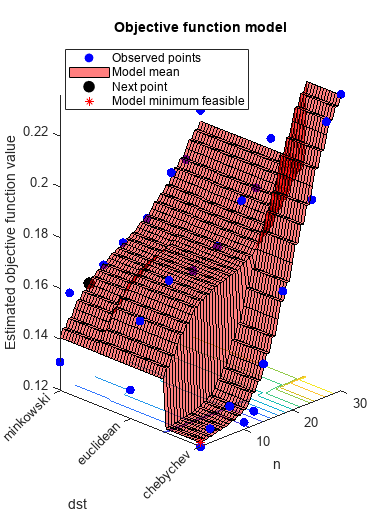
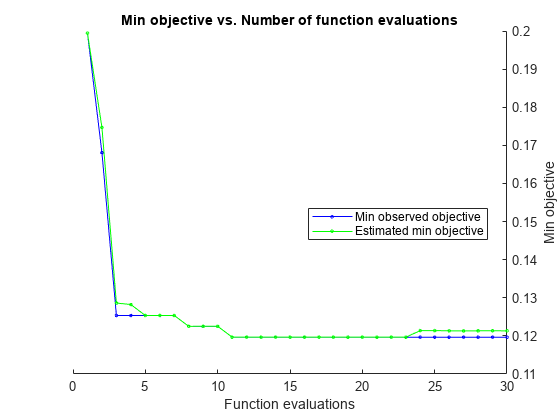
results =
BayesianOptimization with properties:
ObjectiveFcn: @(x)kfoldLoss(fitcknn(X,Y,'CVPartition',c,'NumNeighbors',x.n,'Distance',char(x.dst),'NSMethod','exhaustive'))
VariableDescriptions: [1×2 optimizableVariable]
Options: [1×1 struct]
MinObjective: 0.1197
XAtMinObjective: [1×2 table]
MinEstimatedObjective: 0.1213
XAtMinEstimatedObjective: [1×2 table]
NumObjectiveEvaluations: 30
TotalElapsedTime: 24.1603
NextPoint: [1×2 table]
XTrace: [30×2 table]
ObjectiveTrace: [30×1 double]
ConstraintsTrace: []
UserDataTrace: {30×1 cell}
ObjectiveEvaluationTimeTrace: [30×1 double]
IterationTimeTrace: [30×1 double]
ErrorTrace: [30×1 double]
FeasibilityTrace: [30×1 logical]
FeasibilityProbabilityTrace: [30×1 double]
IndexOfMinimumTrace: [30×1 double]
ObjectiveMinimumTrace: [30×1 double]
EstimatedObjectiveMinimumTrace: [30×1 double]
A coupled constraint is one that can be evaluated only by evaluating the objective function. In this case, the objective function is the cross-validated loss of an SVM model. The coupled constraint is that the number of support vectors is no more than 100. The model details are in Optimize Cross-Validated Classifier Using bayesopt.
Create the data for classification.
rng default grnpop = mvnrnd([1,0],eye(2),10); redpop = mvnrnd([0,1],eye(2),10); redpts = zeros(100,2); grnpts = redpts; for i = 1:100 grnpts(i,:) = mvnrnd(grnpop(randi(10),:),eye(2)*0.02); redpts(i,:) = mvnrnd(redpop(randi(10),:),eye(2)*0.02); end cdata = [grnpts;redpts]; grp = ones(200,1); grp(101:200) = -1; c = cvpartition(200,'KFold',10); sigma = optimizableVariable('sigma',[1e-5,1e5],'Transform','log'); box = optimizableVariable('box',[1e-5,1e5],'Transform','log');
The objective function is the cross-validation loss of the SVM model for partition c. The coupled constraint is the number of support vectors minus 100.5. This ensures that 100 support vectors give a negative constraint value, but 101 support vectors give a positive value. The model has 200 data points, so the coupled constraint values range from -99.5 (there is always at least one support vector) to 99.5. Positive values mean the constraint is not satisfied.
function [objective,constraint] = mysvmfun(x,cdata,grp,c) SVMModel = fitcsvm(cdata,grp,'KernelFunction','rbf',... 'BoxConstraint',x.box,... 'KernelScale',x.sigma); cvModel = crossval(SVMModel,'CVPartition',c); objective = kfoldLoss(cvModel); constraint = sum(SVMModel.IsSupportVector)-100.5;
Pass the partition c and fitting data cdata and grp to the objective function fun by creating fun as an anonymous function that incorporates this data. See Parameterizing Functions.
fun = @(x)mysvmfun(x,cdata,grp,c);
Set the NumCoupledConstraints to 1 so the optimizer knows that there is a coupled constraint. Set options to plot the constraint model.
results = bayesopt(fun,[sigma,box],'IsObjectiveDeterministic',true,... 'NumCoupledConstraints',1,'PlotFcn',... {@plotMinObjective,@plotConstraintModels},... 'AcquisitionFunctionName','expected-improvement-plus','Verbose',0);
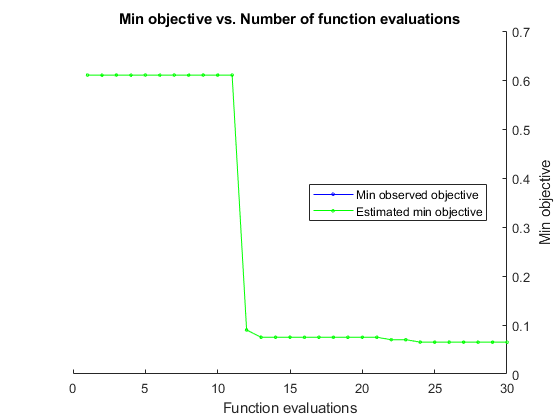
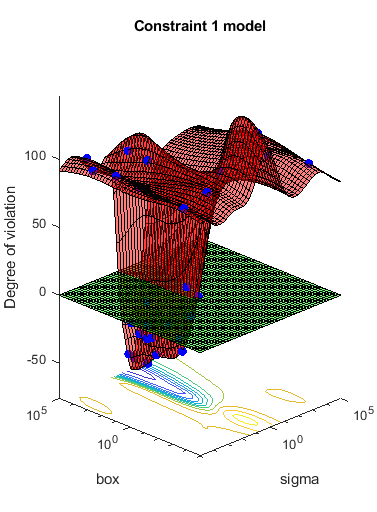
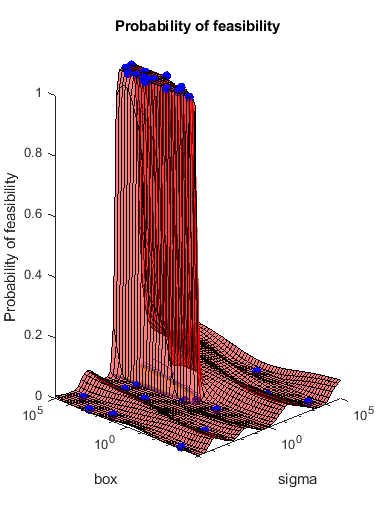
Most points lead to an infeasible number of support vectors.
Improve the speed of a Bayesian optimization by using parallel objective function evaluation.
Prepare variables and the objective function for Bayesian optimization.
The objective function is the cross-validation error rate for the ionosphere data, a binary classification problem. Use fitcsvm as the classifier, with BoxConstraint and KernelScale as the parameters to optimize.
load ionosphere box = optimizableVariable('box',[1e-4,1e3],'Transform','log'); kern = optimizableVariable('kern',[1e-4,1e3],'Transform','log'); vars = [box,kern]; fun = @(vars)kfoldLoss(fitcsvm(X,Y,'BoxConstraint',vars.box,'KernelScale',vars.kern,... 'Kfold',5));
Search for the parameters that give the lowest cross-validation error by using parallel Bayesian optimization.
results = bayesopt(fun,vars,'UseParallel',true);Copying objective function to workers... Done copying objective function to workers.
|===============================================================================================================| | Iter | Active | Eval | Objective | Objective | BestSoFar | BestSoFar | box | kern | | | workers | result | | runtime | (observed) | (estim.) | | | |===============================================================================================================| | 1 | 2 | Accept | 0.2735 | 0.56171 | 0.13105 | 0.13108 | 0.0002608 | 0.2227 | | 2 | 2 | Accept | 0.35897 | 0.4062 | 0.13105 | 0.13108 | 3.6999 | 344.01 | | 3 | 2 | Accept | 0.13675 | 0.42727 | 0.13105 | 0.13108 | 0.33594 | 0.39276 | | 4 | 2 | Accept | 0.35897 | 0.4453 | 0.13105 | 0.13108 | 0.014127 | 449.58 | | 5 | 2 | Best | 0.13105 | 0.45503 | 0.13105 | 0.13108 | 0.29713 | 1.0859 |
| 6 | 6 | Accept | 0.35897 | 0.16605 | 0.13105 | 0.13108 | 8.1878 | 256.9 |
| 7 | 5 | Best | 0.11396 | 0.51146 | 0.11396 | 0.11395 | 8.7331 | 0.7521 | | 8 | 5 | Accept | 0.14245 | 0.24943 | 0.11396 | 0.11395 | 0.0020774 | 0.022712 |
| 9 | 6 | Best | 0.10826 | 4.0711 | 0.10826 | 0.10827 | 0.0015925 | 0.0050225 |
| 10 | 6 | Accept | 0.25641 | 16.265 | 0.10826 | 0.10829 | 0.00057357 | 0.00025895 |
| 11 | 6 | Accept | 0.1339 | 15.581 | 0.10826 | 0.10829 | 1.4553 | 0.011186 |
| 12 | 6 | Accept | 0.16809 | 19.585 | 0.10826 | 0.10828 | 0.26919 | 0.00037649 |
| 13 | 6 | Accept | 0.20513 | 18.637 | 0.10826 | 0.10828 | 369.59 | 0.099122 |
| 14 | 6 | Accept | 0.12536 | 0.11382 | 0.10826 | 0.10829 | 5.7059 | 2.5642 |
| 15 | 6 | Accept | 0.13675 | 2.63 | 0.10826 | 0.10828 | 984.19 | 2.2214 |
| 16 | 6 | Accept | 0.12821 | 2.0743 | 0.10826 | 0.11144 | 0.0063411 | 0.0090242 |
| 17 | 6 | Accept | 0.1339 | 0.1939 | 0.10826 | 0.11302 | 0.00010225 | 0.0076795 |
| 18 | 6 | Accept | 0.12821 | 0.20933 | 0.10826 | 0.11376 | 7.7447 | 1.2868 |
| 19 | 4 | Accept | 0.55556 | 17.564 | 0.10826 | 0.10828 | 0.0087593 | 0.00014486 | | 20 | 4 | Accept | 0.1396 | 16.473 | 0.10826 | 0.10828 | 0.054844 | 0.004479 | |===============================================================================================================| | Iter | Active | Eval | Objective | Objective | BestSoFar | BestSoFar | box | kern | | | workers | result | | runtime | (observed) | (estim.) | | | |===============================================================================================================| | 21 | 4 | Accept | 0.1339 | 0.17127 | 0.10826 | 0.10828 | 9.2668 | 1.2171 |
| 22 | 4 | Accept | 0.12821 | 0.089065 | 0.10826 | 0.10828 | 12.265 | 8.5455 |
| 23 | 4 | Accept | 0.12536 | 0.073586 | 0.10826 | 0.10828 | 1.3355 | 2.8392 |
| 24 | 4 | Accept | 0.12821 | 0.08038 | 0.10826 | 0.10828 | 131.51 | 16.878 |
| 25 | 3 | Accept | 0.11111 | 10.687 | 0.10826 | 0.10867 | 1.4795 | 0.041452 | | 26 | 3 | Accept | 0.13675 | 0.18626 | 0.10826 | 0.10867 | 2.0513 | 0.70421 |
| 27 | 6 | Accept | 0.12821 | 0.078559 | 0.10826 | 0.10868 | 980.04 | 44.19 |
| 28 | 5 | Accept | 0.33048 | 0.089844 | 0.10826 | 0.10843 | 0.41821 | 10.208 | | 29 | 5 | Accept | 0.16239 | 0.12688 | 0.10826 | 0.10843 | 172.39 | 141.43 |
| 30 | 5 | Accept | 0.11966 | 0.14597 | 0.10826 | 0.10846 | 639.15 | 14.75 |
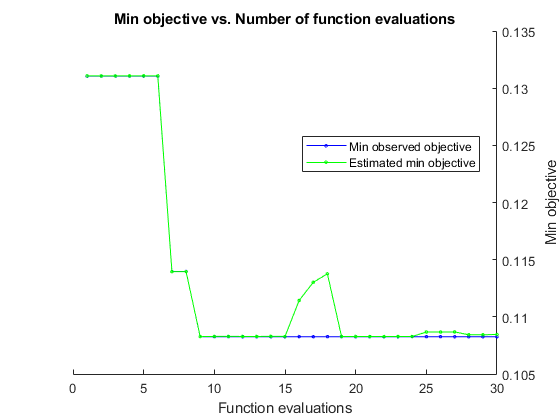
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 48.2085 seconds.
Total objective function evaluation time: 128.3472
Best observed feasible point:
box kern
_________ _________
0.0015925 0.0050225
Observed objective function value = 0.10826
Estimated objective function value = 0.10846
Function evaluation time = 4.0711
Best estimated feasible point (according to models):
box kern
_________ _________
0.0015925 0.0050225
Estimated objective function value = 0.10846
Estimated function evaluation time = 2.8307
Return the best feasible point in the Bayesian model results by using the bestPoint function. Use the default criterion min-visited-upper-confidence-interval, which determines the best feasible point as the visited point that minimizes an upper confidence interval on the objective function value.
zbest = bestPoint(results)
zbest=1×2 table
box kern
_________ _________
0.0015925 0.0050225
The table zbest contains the optimal estimated values for the 'BoxConstraint' and 'KernelScale' name-value pair arguments. Use these values to train a new optimized classifier.
Mdl = fitcsvm(X,Y,'BoxConstraint',zbest.box,'KernelScale',zbest.kern);
Observe that the optimal parameters are in Mdl.
Mdl.BoxConstraints(1)
ans = 0.0016
Mdl.KernelParameters.Scale
ans = 0.0050
Input Arguments
Objective function, specified as a function handle or a parallel.pool.Constant (Parallel Computing Toolbox)
whose Value is a function handle. Typically,
fun returns a measure of loss (such as a
misclassification error) for a machine learning model that has tunable
hyperparameters to control its training. fun has these
signatures:
objective = fun(x) % or [objective,constraints] = fun(x) % or [objective,constraints,UserData] = fun(x)
fun accepts x, a 1-by-D table
of variable values, and returns objective, a real
scalar representing the objective function value fun(x).
Optionally, fun also returns:
constraints, a real vector of coupled constraint violations. For a definition, see Coupled Constraints.constraint(j) > 0means constraintjis violated.constraint(j) < 0means constraintjis satisfied.UserData, an entity of any type (such as a scalar, matrix, structure, or object). For an example of a custom plot function that usesUserData, see Create a Custom Plot Function.
For details about using parallel.pool.Constant with
bayesopt, see Placing the Objective Function on Workers.
Example: @objfun
Data Types: function_handle
Variable descriptions, specified as a vector of optimizableVariable objects
defining the hyperparameters to be tuned.
Example: [X1,X2], where X1 and X2 are optimizableVariable objects
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: results = bayesopt(fun,vars,'AcquisitionFunctionName','expected-improvement-plus')
Algorithm Control
Function to choose next evaluation point, specified as one of the listed choices.
Acquisition functions whose names include
per-second do not yield reproducible results because the optimization
depends on the runtime of the objective function. Acquisition functions whose names include
plus modify their behavior when they are overexploiting an area. For more
details, see Acquisition Function Types.
Example: 'AcquisitionFunctionName','expected-improvement-per-second'
Specify deterministic objective function, specified as false or
true. If fun is stochastic
(that is, fun(x) can return different values for the
same x), then set
IsObjectiveDeterministic to
false. In this case,
bayesopt estimates a noise level during
optimization.
Example: 'IsObjectiveDeterministic',true
Data Types: logical
Propensity to explore, specified as a positive real. Applies
to the 'expected-improvement-plus' and 'expected-improvement-per-second-plus' acquisition
functions. See Plus.
Example: 'ExplorationRatio',0.2
Data Types: double
Fit Gaussian Process model to GPActiveSetSize or
fewer points, specified as a positive integer. When
bayesopt has visited more than
GPActiveSetSize points, subsequent iterations
that use a GP model fit the model to GPActiveSetSize
points. bayesopt chooses points uniformly at random
without replacement among visited points. Using fewer points leads to
faster GP model fitting, at the expense of possibly less accurate
fitting.
Example: 'GPActiveSetSize',80
Data Types: double
Compute in parallel, specified as false (do not
compute in parallel) or true (compute in parallel).
Computing in parallel requires Parallel Computing Toolbox™.
bayesopt performs parallel objective function
evaluations concurrently on parallel workers. For algorithmic details,
see Parallel Bayesian Optimization.
Example: 'UseParallel',true
Data Types: logical
Imputation method for parallel worker objective function values,
specified as 'clipped-model-prediction',
'model-prediction',
'max-observed', or
'min-observed'. To generate a new point to
evaluate, bayesopt fits a Gaussian process to all
points, including the points being evaluated on workers. To fit the
process, bayesopt imputes objective function values
for the points that are currently on workers.
ParallelMethod specifies the method used for
imputation.
'clipped-model-prediction'— Impute the maximum of these quantities:Mean Gaussian process prediction at the point
xMinimum observed objective function among feasible points visited
Minimum model prediction among all feasible points
'model-prediction'— Impute the mean Gaussian process prediction at the pointx.'max-observed'— Impute the maximum observed objective function value among feasible points.'min-observed'— Impute the minimum observed objective function value among feasible points.
Example: 'ParallelMethod','max-observed'
Tolerance on the number of active parallel workers, specified as a
positive integer. After bayesopt assigns a point to
evaluate, and before it computes a new point to assign, it checks
whether fewer than MinWorkerUtilization workers are
active. If so, bayesopt assigns random points
within bounds to all available workers. Otherwise,
bayesopt calculates the best point for one
worker. bayesopt creates random points much faster
than fitted points, so this behavior leads to higher utilization of
workers, at the cost of possibly poorer points. For details, see Parallel Bayesian Optimization.
Example: 'MinWorkerUtilization',3
Data Types: double
Starting and Stopping
Objective function evaluation limit, specified as a positive integer.
Example: 'MaxObjectiveEvaluations',60
Data Types: double
Time limit, specified as a nonnegative real scalar. The time limit is in seconds, as measured
by tic and toc. The software
always performs at least one optimization iteration, regardless of the
value of MaxTime.
Run time can exceed MaxTime because bayesopt does
not interrupt function evaluations.
Example: 'MaxTime',3600
Data Types: double
Number of initial evaluation points, specified as a positive integer.
bayesopt chooses these points randomly within
the variable bounds, according to the setting of the Transform setting for each
variable (uniform for 'none', logarithmically spaced
for 'log').
Example: 'NumSeedPoints',10
Data Types: double
Constraints
Deterministic constraints on variables, specified as a function handle.
For details, see Deterministic Constraints — XConstraintFcn.
Example: 'XConstraintFcn',@xconstraint
Data Types: function_handle
Conditional variable constraints, specified as a function handle.
For details, see Conditional Constraints — ConditionalVariableFcn.
Example: 'ConditionalVariableFcn',@condfun
Data Types: function_handle
Number of coupled constraints, specified as a positive integer. For details, see Coupled Constraints.
Note
NumCoupledConstraints is required when you
have coupled constraints.
Example: 'NumCoupledConstraints',3
Data Types: double
Indication of whether coupled constraints are deterministic, specified
as a logical vector of length NumCoupledConstraints.
For details, see Coupled Constraints.
Example: 'AreCoupledConstraintsDeterministic',[true,false,true]
Data Types: logical
Reports, Plots, and Halting
Command-line display level, specified as 0, 1,
or 2.
0— No command-line display.1— At each iteration, display the iteration number, result report (see the next paragraph), objective function model, objective function evaluation time, best (lowest) observed objective function value, best (lowest) estimated objective function value, and the observed constraint values (if any). When optimizing in parallel, the display also includes a column showing the number of active workers, counted after assigning a job to the next worker.The result report for each iteration is one of the following:
Accept— The objective function returns a finite value, and all constraints are satisfied.Best— Constraints are satisfied, and the objective function returns the lowest value among feasible points.Error— The objective function returns a value that is not a finite real scalar.Infeas— At least one constraint is violated.
2— Same as1, adding diagnostic information such as time to select the next point, model fitting time, indication that "plus" acquisition functions declare overexploiting, and parallel workers are being assigned to random points due to low parallel utilization.
Example: 'Verbose',2
Data Types: double
Function called after each iteration, specified as a function handle or cell array of function handles. An output function can halt the solver, and can perform arbitrary calculations, including creating variables or plotting. Specify several output functions using a cell array of function handles.
There are two built-in output functions:
@assignInBase— Constructs aBayesianOptimizationinstance at each iteration and assigns it to a variable in the base workspace. Choose a variable name using theSaveVariableNamename-value pair.@saveToFile— Constructs aBayesianOptimizationinstance at each iteration and saves it to a file in the current folder. Choose a file name using theSaveFileNamename-value pair.
You can write your own output functions. For details, see Bayesian Optimization Output Functions.
Example: 'OutputFcn',{@saveToFile @myOutputFunction}
Data Types: cell | function_handle
File name for the @saveToFile output function, specified as a character
vector or string scalar. The file name can include a path, such as
'../optimizations/September2.mat'.
Example: 'SaveFileName','September2.mat'
Data Types: char | string
Variable name for the @assignInBase output function, specified as a
character vector or string scalar.
Example: 'SaveVariableName','September2Results'
Data Types: char | string
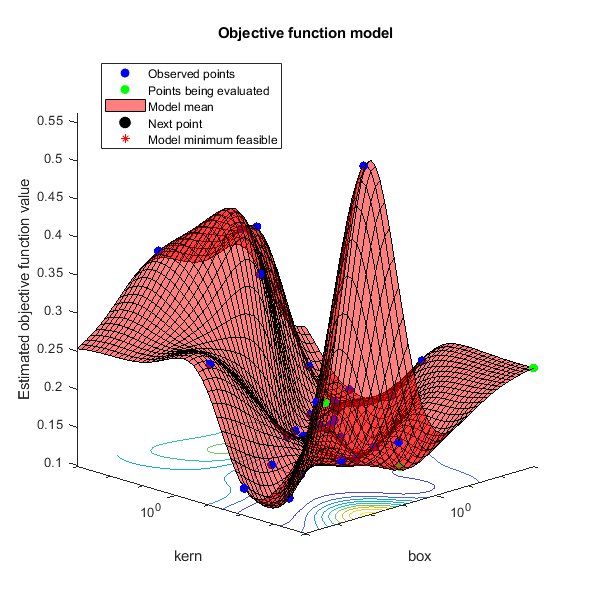
Plot function called after each iteration, specified as 'all',
a function handle, or a cell array of function handles. A plot function
can halt the solver, and can perform arbitrary calculations, including
creating variables, in addition to plotting.
Specify no plot function as [].
'all' calls all built-in plot functions.
Specify several plot functions using a cell array of function handles.
The built-in plot functions appear in the following tables.
| Model Plots — Apply When D ≤ 2 | Description |
|---|---|
@plotAcquisitionFunction | Plot the acquisition function surface. |
@plotConstraintModels | Plot each constraint model surface. Negative values indicate feasible points. Also plot a P(feasible) surface. Also plot the error model, if
it exists, which ranges from Plotted error = 2*Probability(error) – 1. |
@plotObjectiveEvaluationTimeModel | Plot the objective function evaluation time model surface. |
@plotObjectiveModel | Plot the |
| Trace Plots — Apply to All D | Description |
|---|---|
@plotObjective | Plot each observed function value versus the number of function evaluations. |
@plotObjectiveEvaluationTime | Plot each observed function evaluation run time versus the number of function evaluations. |
@plotMinObjective | Plot the minimum observed and estimated function values versus the number of function evaluations. |
@plotElapsedTime | Plot three curves: the total elapsed time of the optimization, the total function evaluation time, and the total modeling and point selection time, all versus the number of function evaluations. |
You can write your own plot functions. For details, see Bayesian Optimization Plot Functions.
Note
When there are coupled constraints, iterative display and plot functions can give counterintuitive results such as:
A minimum objective plot can increase.
The optimization can declare a problem infeasible even when it showed an earlier feasible point.
The reason for this behavior is that the decision about whether
a point is feasible can change as the optimization progresses. bayesopt determines
feasibility with respect to its constraint model, and this model changes
as bayesopt evaluates points. So a “minimum
objective” plot can increase when the minimal point is later
deemed infeasible, and the iterative display can show a feasible point
that is later deemed infeasible.
Example: 'PlotFcn','all'
Data Types: char | string | cell | function_handle
Initialization
Initial evaluation points, specified as an N-by-D table,
where N is the number of evaluation points, and D is
the number of variables.
Note
If only InitialX is provided, it is interpreted
as initial points to evaluate. The objective function is evaluated
at InitialX.
If any other initialization parameters are also provided, InitialX is
interpreted as prior function evaluation data. The objective function
is not evaluated. Any missing values are set to NaN.
Data Types: table
Objective values corresponding to InitialX,
specified as a length-N vector, where
N is the number of evaluation points.
Example: 'InitialObjective',[17;-3;-12.5]
Data Types: double
Constraint violations of coupled constraints, specified as an N-by-K matrix,
where N is the number of evaluation points and K is
the number of coupled constraints. For details, see Coupled Constraints.
Data Types: double
Errors for InitialX, specified as a length-N vector
with entries -1 or 1, where N is
the number of evaluation points. Specify -1 for
no error, and 1 for an error.
Example: 'InitialErrorValues',[-1,-1,-1,-1,1]
Data Types: double
Initial data corresponding to InitialX,
specified as a length-N cell vector, where N is
the number of evaluation points.
Example: 'InitialUserData',{2,3,-1}
Data Types: cell
Evaluation times of objective function at InitialX,
specified as a length-N vector, where N is
the number of evaluation points. Time is measured in seconds.
Data Types: double
Times for the first N iterations, specified
as a length-N vector, where N is
the number of evaluation points. Time is measured in seconds.
Data Types: double
Output Arguments
Bayesian optimization results, returned as a BayesianOptimization object.
More About
Coupled constraints are those constraints whose value comes from the objective function calculation. See Coupled Constraints.
Tips
Bayesian optimization is not reproducible if one of these conditions exists:
You specify an acquisition function whose name includes
per-second, such as'expected-improvement-per-second'. Theper-secondmodifier indicates that optimization depends on the run time of the objective function. For more details, see Acquisition Function Types.You specify to run Bayesian optimization in parallel. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For more details, see Parallel Bayesian Optimization.
Extended Capabilities
To run in parallel, set the UseParallel name-value argument to
true in the call to this function.
For more general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2016bbayesopt defaults to serial computation when
UseParallel=true and the software cannot open a parallel
pool.
In previous releases, the software issues an error under these circumstances.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)