このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

PMSM

正弦波の磁束分布をもつ永久磁石同期モーター

• 

ライブラリ:
Simscape / Electrical / Electromechanical / Permanent Magnet

説明

PMSM ブロックは、三相 Y 結線固定子、デルタ結線固定子、または開放端固定子をもつ永久磁石同期モーター (PMSM) をモデル化します。このブロックを使用して、埋込永久磁石同期モーター (IPMSM)、表面永久磁石同期モーター (SPMSM)、横方向磁束モーター、軸方向磁束 (パンケーキ) モーター、または PMSM サーボモーターをモデル化します。

PMSM には永久磁石回転子と結線固定子が含まれています。これらのモーターは、電気自動車 (EV) などの牽引アプリケーションや作動システムで使用できます。作動システムでは、PMSM は "ブラシレス サーボモーター" とも呼ばれます。PMSM は一般的に、台形逆起電力プロファイルをもつブラシレス直流 (BLDC) モーターと比較して、望ましくない高周波数の機械的および電気的な電流高調波を削減する正弦波逆起電力プロファイルを持っています。

PMSM ブロックは、固定の d 軸および q 軸のインダクタンス Ld および Lq をもつモーターをモデル化します。このブロックを使用して、次の 2 つの主要なタイプの PMSM をモデル化できます。

• SPMSM (表面永久磁石 (SPM) モーター) — 回転子の磁石が表面実装されています。Ld と Lq は等しくなっています。

• IPMSM (埋込永久磁石 (IPM) モーター) — 回転子の磁石が回転子の内部にあります。Ld と Lq は等しくありません。

主磁束路に基づいて PMSM を分類することもできます。主磁束路は一般に半径方向ですが、軸方向にすることもできます。後者の場合、同じ物理サイズのモーターでトルクが大幅に大きくなります。PMSM ブロックを使用して、半径方向と軸方向の両方の磁束の PMSM をモデル化できます。

[結線種別] パラメーターを使用して、結線の構成を指定できます。次の図は、Y 結線固定子の等価電気回路を示しています。

[結線種別] を [デルタ結線] または [開放端] に設定して、それぞれデルタ巻線固定子または開放端固定子をモデル化することもできます。

このブロックではさまざまな組み込みのパラメーター化を選択できます。詳細については、事前定義されたパラメーター化セクションを参照してください。

メモ

Simscape™ Electrical™ には、同じタイプのモーターまたはアクチュエータをモデル化できる複数のブロックが含まれています。回答が必要なエンジニアリング設計の質問に対して十分なモデル化の詳細を備えたブロックを選択してください。ただし、モデルの忠実度が高いほどシミュレーションが遅くなり、パラメーター化がより複雑になるため、必要以上の詳細なモデル化をもつブロックを使用しないでください。

PMSM ブロックのようなブロックは、固定係数またはパラメーター依存の係数をもち、単純な等価回路をもつモーターをモデル化します。これらのモデルの忠実度は中レベルです。このブロックは、ロボティクスやメカトロニクスなどの作動アプリケーションでの制御やシステムの設計、および飽和や高調波が損失に少しだけ影響する場合の効率の予測に使用します。適切な忠実度でモーターをモデル化するための適切なブロックの選択の詳細については、Choose Blocks to Model Motors or Actuatorsを参照してください。

モーターの構造

次の図は、回転子に単一の極対があるモーターの構造を示しています。

永久磁石によって回転子の磁場が生成され、これにより回転子の角度に基づく正弦波の磁束変化率が得られます。

座標軸の規則で、[回転子の角度の定義] パラメーターを [A 相の磁気軸と d 軸の間の角度] に設定すると、回転子の機械的角度 θ_r が 0 の場合に a 相と永久磁石の磁束が揃います。[回転子の角度の定義] パラメーターを [A 相の磁気軸と q 軸の間の角度] に設定すると、回転子の機械的角度は a 相の磁気軸と回転子の q 軸の間の角度になります。

方程式

固定子巻線にかかる電圧は次のとおりです。

$$\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right]=\left[\begin{array}{ccc}{R}_s& 0& 0\\ 0& R_s& 0\\ 0& 0& R_s\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+\left[\begin{array}{c}\frac{d{\psi }_a}{dt}\\ \frac{d{\psi }_b}{dt}\\ \frac{d{\psi }_c}{dt}\end{array}\right],$$

ここで、

• v_a、v_b、および v_c は、固定子巻線にかかる個々の相電圧です。

• R_s は、各固定子巻線の等価抵抗です。

• i_a、i_b、および i_c は、固定子巻線に流れる電流です。

• $$\frac{d{\psi }_a}{dt},$$、$$\frac{d{\psi }_b}{dt},$$、および $$\frac{d{\psi }_c}{dt}$$ は、各固定子巻線の磁束の変化率です。

永久磁石と 3 本の巻線は、各巻線を鎖交する合計磁束に寄与します。合計磁束は次のとおりです。

$$\left[\begin{array}{c}{\psi }_a\\ {\psi }_b\\ {\psi }_c\end{array}\right]=\left[\begin{array}{ccc}{L}_{aa}& L_{ab}& L_{ac}\\ L_{ba}& L_{bb}& L_{bc}\\ L_{ca}& L_{cb}& L_{cc}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]+\left[\begin{array}{c}{\psi }_{am}\\ {\psi }_{bm}\\ {\psi }_{cm}\end{array}\right],$$

ここで、

• ψ_a、ψ_b、および ψ_c は、各固定子巻線を鎖交する合計磁束です。

• L_aa、L_bb、および L_cc は、固定子巻線の自己インダクタンスです。

• L_ab、L_ac、L_ba などは、固定子巻線の相互インダクタンスです。

• ψ_am、ψ_bm、および ψ_cm は、固定子巻線を鎖交する永久磁石の磁束です。

固定子巻線のインダクタンスは回転子の電気角の関数で、次のように定義されます。

${\theta }_e=N{\theta }_r+rotoroffset$

$L_{aa}=L_s+L_m\text{cos}(2{\theta }_e)$

$L_{bb}=L_s+L_m\text{cos}(2\left({\theta }_e-2\pi /3\right))$

$L_{cc}=L_s+L_m\text{cos}(2\left({\theta }_e+2\pi /3\right))$

$$L_{ab}=L_{ba}=-M_s-L_m\cos \left(2\left({\theta }_e+\pi /6\right)\right)$$

$L_{bc}=L_{cb}=-M_s-L_m\cos \left(2\left({\theta }_e+\pi /6-2\pi /3\right)\right)$

$L_{ca}=L_{ac}=-M_s-L_m\cos \left(2\left({\theta }_e+\pi /6+2\pi /3\right)\right)$

ここで、

• θ_r は回転子の機械的角度です。

• θ_e は回転子の電気角です。

• rotor offset は、d 軸に対する回転子の電気角を定義する場合は 0 で、q 軸に対する回転子の電気角を定義する場合は -pi/2 です。

• L_s は固定子の相あたりの自己インダクタンスです。この値は、各固定子巻線の平均自己インダクタンスです。

• L_m は固定子のインダクタンス変動です。この値は、回転子の角度の変化に伴う自己インダクタンスと相互インダクタンスの変動量です。

• M_s は固定子の相互インダクタンスです。この値は、固定子巻線間の平均相互インダクタンスです。

巻線 a を鎖交する永久磁石の磁束は、θ_e = 0° のときに最大になり、θ_e = 90° のときにゼロになります。したがって、鎖交したモーター磁束は次のように定義されます。

$$\left[\begin{array}{c}{\psi }_{am}\\ {\psi }_{bm}\\ {\psi }_{cm}\end{array}\right]=\left[\begin{array}{c}{\psi }_m\cos {\theta }_e\\ {\psi }_m\cos \left({\theta }_e-2\pi /3\right)\\ {\psi }_m\cos \left({\theta }_e+2\pi /3\right)\end{array}\right]$$

ここで、ψ_m は永久磁石の鎖交磁束です。

簡易電気方程式

ブロックの電気方程式に Park 変換を適用すると、回転子の角度に依存しないトルクの式が得られます。

Park 変換は次のように定義されます。

$P=2/3\left[\begin{array}{ccc}\cos {\theta }_e& \cos \left({\theta }_e-2\pi /3\right)& \cos \left({\theta }_e+2\pi /3\right)\\ -\sin {\theta }_e& -\sin \left({\theta }_e-2\pi /3\right)& -\sin \left({\theta }_e+2\pi /3\right)\\ 0.5& 0.5& 0.5\end{array}\right]$

ここで、θ_e は Nθ_r として定義される電気角です。N は極対数です。

固定子巻線の電圧と電流に対して Park 変換を使用すると、その電圧と電流は回転子の角度に依存しない dq0 座標系に変換されます。

$$\left[\begin{array}{c}{v}_d\\ v_q\\ v_0\end{array}\right]=P\left[\begin{array}{c}{v}_a\\ v_b\\ v_c\end{array}\right]$$

$\left[\begin{array}{c}{i}_d\\ i_q\\ i_0\end{array}\right]=P\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$

最初の 2 つの電気方程式に Park 変換を適用すると、ブロックの動作を定義する次の方程式が得られます。

$v_d=R_s{i}_d+L_d\frac{d{i}_d}{dt}-N\omega i_q{L}_q$

$v_q=R_s{i}_q+L_q\frac{d{i}_q}{dt}+N\omega (i_d{L}_d+{\psi }_m)$

$v_0=R_s{i}_0+L_0\frac{d{i}_0}{dt}$

$T=\frac{3}{2}N\left(i_q\left(i_d{L}_d+{\psi }_m\right)-i_d{i}_q{L}_q\right)$

ここで、

• L_d = L_s + M_s + 3/2 L_m。L_d は固定子の d 軸インダクタンスです。

• L_q = L_s + M_s − 3/2 L_m。L_q は固定子の q 軸インダクタンスです。

• L₀ = L_s – 2M_s。L₀ は固定子の零相インダクタンスです。

• ω は回転子の機械回転速度です。

• N は回転子の永久磁石の極対数です。

• T は回転子のトルクです。トルクはモーターのケース (ブロックの物理端子 C) からモーターの回転子 (ブロックの物理端子 R) へと流れます。

PMSM ブロックは、Park 変換の元の非直交実装を使用します。代替の実装の適用を試みると、dq0 電圧および電流について異なる結果が得られます。

代替の鎖交磁束のパラメーター化

[永久磁石の鎖交磁束] パラメーターを使用して、モーターのデータシートに一般的に記載されている逆起電力定数またはトルク定数を使用してモーターをパラメーター化できます。

逆起電力定数は、各相の pu 単位での回転速度において永久磁石によって誘起されるピーク電圧です。永久磁石のピーク鎖交磁束と逆起電力の関係は次のとおりです。

$$k_e=N{\psi }_m.$$

1 相分の逆起電力 e_ph は次のとおりです。

$$e_{ph}=k_e\omega .$$

トルク定数は、各相の pu 単位での電流によって誘起されるピーク トルクです。これと逆起電力定数の両方を SI 単位系で表した場合、それらの値は数値的に同じになります。

$$k_t=N{\psi }_m.$$

L_d=L_q の場合に、3 相すべての電流が平衡していると、結合されたトルク T は次のようになります。

$$T=\frac{3}{2}{k}_t{i}_q=\frac{3}{2}{k}_t{I}_{pk},$$

ここで、I_pk は 3 本の巻線いずれかのピーク電流です。

係数 3/2 は、これが全相のトルクの定常状態の和であることに基づいています。したがって、トルク定数 k_t は次のようにもなります。

$$k_t=\frac{2}{3}\left(\frac{T}{I_{pk}}\right),$$

ここで、T はピーク線電圧での平衡三相電流 I_pk を使用してテストする場合に測定される合計トルクです。実効値線電流は次のとおりです。

$$k_t=\frac{\sqrt{2}}{3}\frac{T}{i_{line,rms}}.$$

鉄損の計算

鉄損は 2 項に分けられます。一方は主磁化路を表し、もう一方は弱め界磁操作中にアクティブになるクロス歯路を表します。鉄損モデルは、[3]に基づいています。

主磁化路を表す項は、固定子の誘起された実効値線-中性点電圧 $$V_{m_{rms}}^{}$$ によって異なります。

$$P_{OC}\left(V_{m_{rms}}^{}\right)=\frac{a_h}{k}{V}_{m_{rms}}^{}+\frac{a_j}{k^2}{V}_{m_{rms}}^2+\frac{a_{ex}}{k^{1.5}}{V}_{m_{rms}}^{1.5}.$$

これは無負荷状態における主要項です。k は、実効値電圧 V/Hz を使った逆起電力定数です。これは $$k=V_{m_{rms}}^{}/f$$ として定義されます。ここで、f は電気周波数です。右辺の第 1 項は磁気ヒステリシス損失、第 2 項は渦電流損失、第 3 項は過剰損失です。分子にある 3 つの係数は、開回路のヒステリシス損失、渦損失、および過剰損失に指定した値から導出されます。

クロス歯路を表す項は、反磁界が設定されている場合に重要となり、有限要素解析の短絡テストで特定できます。クロス歯磁束に関連付けられた実効値起電力 $$V_{d_{rms}}^{*}$$ によって異なります。

$$P_{SC}\left(V_{d_{rms}}^{*}\right)=\frac{b_h}{k}{V}_{d_{rms}}^{*}+\frac{b_j}{k^2}{V}_{d_{rms}}^{*2}+\frac{b_{ex}}{k^{1.5}}{V}_{d_{rms}}^{*1.5}.$$

3 つの分子項は、短絡のヒステリシス損失、渦損失、および過剰損失に指定した値から導出されます。

事前定義されたパラメーター化

PMSM ブロックでは複数の組み込みのパラメーター化を使用できます。

この事前にパラメーター化されたデータを使用すると、特定のサプライヤーのコンポーネントを表すようにブロックを設定できます。これらの永久磁石同期モーターのパラメーター化は製造元のデータ シートと一致しています。事前定義されたパラメーター化を読み込むには、PMSM ブロックをダブルクリックし、[選択したパーツ] パラメーターの [<クリックして選択>] ハイパーリンクをクリックして、ブロック パラメーター化マネージャーのウィンドウで、利用可能なコンポーネントのリストから使用するパーツを選択します。

メモ

Simscape コンポーネントの事前定義されたパラメーター化では、パラメーターの値に入手可能なデータ ソースを使用しています。工学的判断と仮定の簡略化を使用して、欠損データが埋められます。その結果、シミュレーションと実際の物理的動作にずれが生じることが想定されます。精度を確保するために、シミュレーションの動作を実験データに対して検証し、必要に応じてコンポーネント モデルを調整します。

事前のパラメーター化の詳細と利用可能なコンポーネントのリストについては、事前にパラメーター化されたコンポーネントのリストを参照してください。

熱効果のモデル化

熱端子を表示して、電力を熱に変換する損失の影響をモデル化できます。熱端子を表示するには、[モデリング オプション] パラメーターを次のどちらかに設定します。

• 熱端子なし — ブロックには、固定子巻線に関連付けられた展開された電気量保存端子が含まれますが、熱端子は含まれません。

• 熱端子を表示 — ブロックには、固定子巻線に関連付けられた展開された電気量保存端子と、各巻線および回転子用の熱保存端子が含まれます。

アクチュエータ ブロックにおける熱端子の使い方の詳細については、回転アクチュエータおよび並進アクチュエータでの熱効果のシミュレーションを参照してください。

変数

シミュレーションの前にブロック変数の優先順位と初期ターゲット値を設定するには、ブロックのダイアログ ボックスまたはプロパティ インスペクターの [初期ターゲット] セクションを使用します。詳細については、ブロック変数の優先順位と初期ターゲットの設定を参照してください。

ノミナル値は、モデル内で予想される変数の大きさを指定する方法を提供します。ノミナル値に基づくシステムのスケーリングを使用すると、シミュレーションのロバスト性が向上します。ノミナル値は、ブロックのダイアログ ボックスまたはプロパティ インスペクターの [ノミナル値] セクションなど、さまざまなソースを使用して指定できます。詳細については、ノミナル値によるシステムのスケーリングを参照してください。

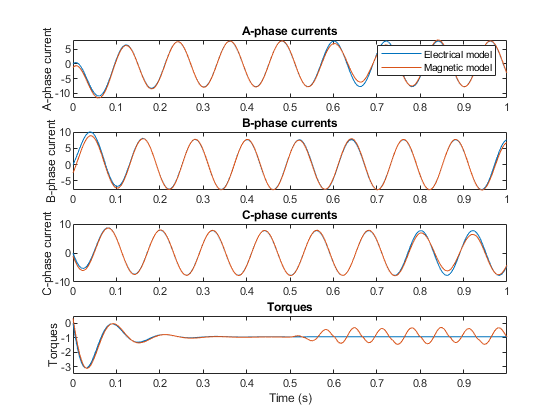
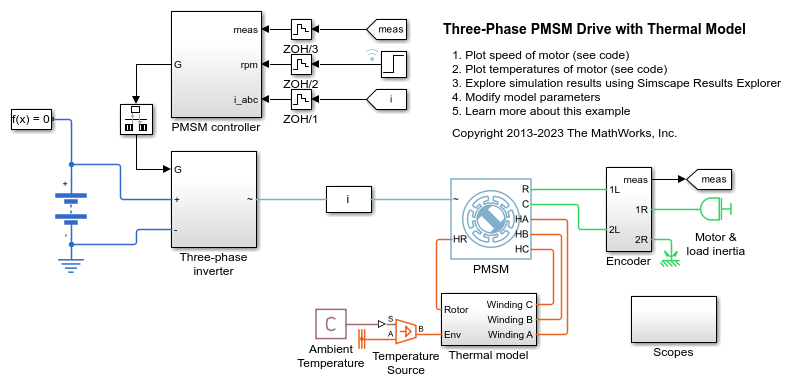
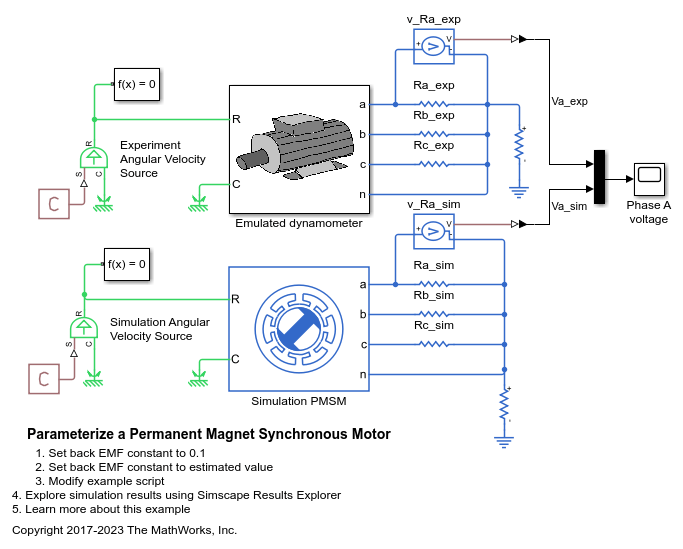
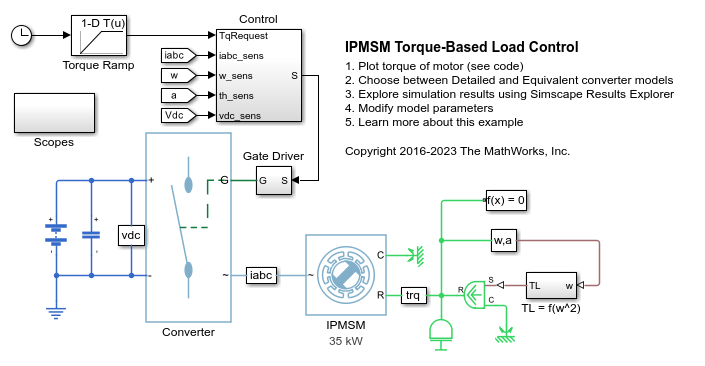
例

電動パワー ステアリング

この例では、永久磁石同期電動機 (PMSM) を使用して、自動車のパワー ステアリング システムでドライバーがかけた力を増幅する方法を説明します。

• モデルを開く

故障した PMSM

この例では、Simscape™ Electrical™ を使用して故障した永久磁石同期モーター (PMSM) をモデル化する方法を説明します。一般的に、PMSM をモデル化するときには、各巻線を、関連するインダクタンス、誘起逆起電力 (EMF)、および隣接する巻線との相互誘導結合をもつ単一のエンティティとして表すことができます。しかし、巻線が故障した場合、単一エンティティの仮定が破綻します。結果のダイナミクスを正しく取得するには、巻線スロットのレベルでモーターをモデル化しなければなりません。このためには、磁気ドメインでモデル化する必要があります。

• モデルを開く

三相 PMSM 駆動

この例では、Y 結線およびデルタ結線構成内の永久磁石同期機 (PMSM) と、一般的なハイブリッド車両用にサイズ設定されたインバーターを説明します。インバーターは車両バッテリーに直接接続されていますが、中間に DC-DC コンバーター段階を実装することもできます。このモデルを使用すると、望ましい性能を達成するためのアーキテクチャとゲインを選択することにより、PMSM コントローラーを設計できます。IGBT をオンまたはオフにするタイミングをチェックするために、IGBT デバイスをより詳細な N-Channel IGBT ブロックに置き換えることができます。車両全体のモデル化には、Motor & Drive (System Level) ブロックを使用して、PMSM、インバーター、およびコントローラーを、エネルギーベースのモデルで抽象化することができます。Gmin 抵抗は、非常に小さなコンダクタンスを接地に与え、可変ステップ ソルバーを使用する場合にモデルの数値的な特性を改善します。

• モデルを開く

熱モデルをもつ三相 PMSM 駆動

この例では、一般的なハイブリッド車両用にサイズ設定された PMSM (永久磁石同期機) とインバーターについて説明します。PMSM には、熱モデルと経験的な鉄損が含まれています。インバーターは車両バッテリーに直接接続されていますが、中間に DC-DC コンバーター段階を実装することもできます。このモデルを使用すると、望ましい性能を達成するためのアーキテクチャとゲインを選択することにより、PMSM コントローラーを設計できます。固定子巻線と回転子の初期温度は摂氏 25 度に設定されています。周囲温度は摂氏 27 度です。Scopes サブシステムには、シミュレーション結果を確認できるスコープが含まれています。

• モデルを開く

永久磁石同期電動機のパラメーター化

この例では、鎖交磁束が未知であるブラックボックスの永久磁石同期電動機 (PMSM) の逆起電力定数とトルク定数を推定する方法を説明します。逆起電力定数またはトルク定数のどちらかを使用して鎖交磁束を記述し、Simscape™ Electrical™ の PMSM ブロックをパラメーター化することができます。このパラメーター化によって、ブラックボックスであるモーターの動作をシミュレーションで正確に再現することができます。

• モデルを開く

IPMSM トルク制御

この例では、埋込永久磁石同期機 (IPMSM) をベースとする自動車の電気牽引駆動装置において、トルクを制御する方法を説明します。高圧バッテリーは、制御された三相コンバーターを通して IPMSM に電力を供給します。IPMSM は、負荷に応じてモーター モードと発電機モードの両方で動作します。理想的な角速度源が負荷を提供します。Control サブシステムは、IPMSM のトルク制御に開ループ アプローチを使用し、電流制御に閉ループ アプローチを使用します。各サンプル瞬時において、トルク要求は関連する指令電流に変換されます。電流制御は PI ベースであり、トルク制御に使用されるレートよりも速いサンプルレートを使用します。シミュレーションでは、モーター モードと発電機モードの両方で、複数のトルク ステップを使用します。タスク スケジューリングは Stateflow® で設計します。Scopes サブシステムには、シミュレーション結果を確認できるスコープが含まれています。

• モデルを開く

IPMSM のトルクベースの負荷制御

この例では、埋込永久磁石同期モーター (IPMSM) をベースとする駆動装置においてトルクを制御する方法を説明します。高圧バッテリーは、制御された三相インバーターを通して IPMSM に電力を供給します。トルク要求の上昇がモーター コントローラーに対して指定されます。負荷トルクは、回転子の速度に二次的に依存します。Control サブシステムは、IPMSM のトルク制御に開ループ アプローチを使用し、電流制御に閉ループ アプローチを使用します。各サンプル瞬時において、トルク要求は関連する指令電流に変換されます。電流制御は PI ベースであり、トルク制御に使用されるレートよりも速いサンプルレートを使用します。タスク スケジューリングは Stateflow® で設計します。Scopes サブシステムには、シミュレーション結果を確認できるスコープが含まれています。

• モデルを開く

IPMSM の速度制御

この例では、埋込永久磁石同期機 (IPMSM) をベースとする自動車の電気牽引駆動装置において、回転子の角速度を制御する方法を説明します。高圧バッテリーは、制御された三相コンバーターを通して IPMSM に電力を供給します。IPMSM は、負荷に応じてモーター モードと発電機モードの両方で動作します。理想的なトルク源が負荷を提供します。Scopes サブシステムには、シミュレーション結果を確認できるスコープが含まれています。Control サブシステムには、外側の角速度制御ループと内側の 2 つの電流制御ループをもつ、マルチレートの PI ベース カスケード制御構造が含まれています。Control サブシステムのタスク スケジューリングは、Stateflow® のステート マシンとして実装されます。1 秒間のシミュレーション中、角速度要求は 0 rpm、500 rpm、2000 rpm、3000 rpm になります。

• モデルを開く

Control Velocity of Three-Phase PMSM with Open-End Winding

Control the rotor angular velocity in an interior permanent magnet synchronous machine (IPMSM) with an open-end winding. A high-voltage battery feeds the IPMSM through two controlled three-phase converters. The IPMSM operates in both motoring and generating modes according to the load. An ideal torque source provides the load. The Scopes subsystem contains scopes that allow you to see the simulation results. The Control subsystem includes a PI-based field oriented control structure. During the one-second simulation, the angular velocity demand is 0 rpm, 500 rpm, 2000 rpm, and then 3000 rpm.

• R2025a 以降
• モデルを開く

IPMSM の外側ループ コントローラーの評価

この例では、埋込永久磁石同期機 (IPMSM) をベースとする電気牽引駆動装置において、回転子の角速度を制御する方法を説明します。外側ループの速度コントローラーの評価では、内側ループの電流コントローラーは、三相制御電流源に置き換えられます。理想的なトルク源が負荷を提供します。Scopes サブシステムには、シミュレーション結果を確認できるスコープが含まれています。Control サブシステムには、PI ベースの外側ループ コントローラーが含まれています。3 秒間のシミュレーション中、角速度要求は -1000 rpm、2000 rpm、3000 rpm、4000 rpm、5000 rpm になります。

• モデルを開く

端子

保存

~ — 三相端子

電気

展開可能な三相端子。詳細については、三相端子を参照してください。

依存関係

この端子を有効にするには、[電気的接続] を [複合三相端子] に、[結線種別] を [Y 結線] または [デルタ結線] に設定します。

a — a 相

電気

a 相に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [Y 結線] または [デルタ結線] に設定します。

b — b 相

電気

b 相に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [Y 結線] または [デルタ結線] に設定します。

c — c 相

電気

c 相に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [Y 結線] または [デルタ結線] に設定します。

~1 — 固定子の正側接続

電気

R2024a 以降

固定子の正側接続に関連付けられた展開可能な三相端子。

依存関係

この端子を有効にするには、[電気的接続] を [複合三相端子] に、[結線種別] を [開放端] に設定します。

~2 — 固定子の負側接続

電気

R2024a 以降

固定子の負側接続に関連付けられた展開可能な三相端子。

依存関係

この端子を有効にするには、[電気的接続] を [複合三相端子] に、[結線種別] を [開放端] に設定します。

a1 — a の正側接続

電気

R2024a 以降

a の正側接続に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [開放端] に設定します。

b1 — b の正側接続

電気

R2024a 以降

b の正側接続に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [開放端] に設定します。

c1 — c の正側接続

電気

R2024a 以降

c の正側接続に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [開放端] に設定します。

a2 — a の負側接続

電気

R2024a 以降

a の負側接続に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [開放端] に設定します。

b2 — b の負側接続

電気

R2024a 以降

b の負側接続に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [開放端] に設定します。

c2 — c の負側接続

電気

R2024a 以降

c の負側接続に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[電気的接続] を [展開三相端子] に、[結線種別] を [開放端] に設定します。

n — 中性相

電気

中性相に関連付けられた電気量保存端子。

依存関係

この端子を有効にするには、[結線種別] を [Y 結線] に、[零相] を [含める] に設定します。

R — モーターの回転子

機械

モーターの回転子に関連付けられた機械回転保存端子。

C — モーターのケース

機械

モーターのケースに関連付けられた機械回転保存端子。

HA — 巻線 A の熱端子

熱

巻線 A に関連付けられた熱保存端子。

依存関係

この端子を有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

HB — 巻線 B の熱端子

熱

巻線 B に関連付けられた熱保存端子。

依存関係

この端子を有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

HC — 巻線 C の熱端子

熱

巻線 C に関連付けられた熱保存端子。

依存関係

この端子を有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

HR — 回転子の熱端子

熱

回転子に関連付けられた熱保存端子。

依存関係

この端子を有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

パラメーター

選択したパーツ — 事前定義されたパラメーター化オプション

<クリックして選択> (既定値)

特定のサプライヤーのコンポーネントを表すようにブロックをパラメーター化するオプション。[<クリックして選択>] ハイパーリンクをクリックすると、ブロック パラメーター化マネージャーのウィンドウが開きます。ブロック パラメーター化マネージャーの詳細については、事前定義されたパラメーター化の読み込みを参照してください。

モデリング オプション — 熱端子を有効にするかどうか

熱端子なし (既定値) | 熱端子を表示

ブロックの熱端子を有効にして、電力を熱に変換する損失の影響をモデル化するかどうか。

メイン

電気的接続 — 電気的接続

複合三相端子 (既定値) | 展開三相端子

複合三相端子と展開三相端子のどちらを使用するか。

結線種別 — 巻線の構成

Y 結線 (既定値) | デルタ結線 | 開放端

巻線の構成を選択します。

• Y 結線 — 巻線は Y 結線です。

• デルタ結線 — 巻線はデルタ結線です。a 相は端子 a と端子 b の間、b 相は端子 b と端子 c の間、c 相は端子 c と端子 a の間に接続されます。

• 開放端 — 巻線は開放端構成内にあります。ブロックに、巻線の各端が電気的接続として表示されます。

モデル化の忠実度 — モデル化の忠実度

定数の Ld、Lq、および PM (既定値) | 表形式の Ld、Lq、および PM

モデル化の忠実度を選択します。

• 定数の Ld、Lq、および PM — Ld、Lq、および PM の値は定数で、それぞれのパラメーターで定義されます。

• 表形式の Ld、Lq、および PM — Ld、Lq、および PM の値は、次のように DQ 電流ルックアップ テーブルからオンラインで計算されます。

  $$L_d=f_1(i_d,i_q)$$

  $$L_d=f_2(i_d,i_q)$$

  $${\lambda }_{PM}=f_2(i_d,i_q)$$

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に設定します。

極対数 — 極対数

6 (既定値)

回転子の永久磁石の極対数。

永久磁石の鎖交磁束のパラメーター化 — 永久磁石の鎖交磁束のパラメーター化

鎖交磁束を指定 (既定値) | トルク定数を指定 | 逆起電力定数を指定

[鎖交磁束を指定]、[トルク定数を指定]、または [逆起電力定数を指定] を選択します。

永久磁石の鎖交磁束 — 永久磁石の鎖交磁束

0.03 [Wb] (既定値)

いずれかの固定子巻線における永久磁石のピーク鎖交磁束。

依存関係

このパラメーターを有効にするには、[永久磁石の鎖交磁束のパラメーター化] を [鎖交磁束を指定] に、[モデル化の忠実度] を [定数の Ld、Lq、および PM] に設定します。

トルク定数 — トルク定数

0.18 [N*m/A] (既定値)

いずれかの固定子巻線におけるトルク定数。

依存関係

このパラメーターを有効にするには、[永久磁石の鎖交磁束のパラメーター化] を [トルク定数を指定] に、[モデル化の忠実度] を [定数の Ld、Lq、および PM] に設定します。

逆起電力定数 — 逆起電力定数

0.18 [V*s/rad] (既定値)

いずれかの固定子巻線における逆起電力定数。

メモ

逆起電力定数は、各相の pu 単位での回転速度において永久磁石によって誘起されるピーク電圧です。Y 結線モーターの場合、この電圧は線-中性点電圧です。

依存関係

このパラメーターを有効にするには、[永久磁石の鎖交磁束のパラメーター化] を [逆起電力定数を指定] に、[モデル化の忠実度] を [定数の Ld、Lq、および PM] に設定します。

固定子のパラメーター化 — 固定子のパラメーター化

Ld、Lq、L0 を指定 (既定値) | Ls、Lm、Ms を指定

[Ld、Lq、L0 を指定] または [Ls、Lm、Ms を指定] を選択します。

固定子の d 軸インダクタンス、Ld — 固定子の d 軸インダクタンス

0.00022 [H] (既定値)

d 軸インダクタンス。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に、[モデル化の忠実度] を [定数の Ld、Lq、および PM] に設定します。

固定子の q 軸インダクタンス、Lq — 固定子の q 軸インダクタンス

0.00022 [H] (既定値)

q 軸インダクタンス。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に、[モデル化の忠実度] を [定数の Ld、Lq、および PM] に設定します。

直軸電流ベクトル、iD — 直軸電流ベクトル

[-200, 0, 200] [A] (既定値)

直軸電流ベクトル、iD。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に、[モデル化の忠実度] を [表形式の Ld、Lq、および PM] に設定します。

横軸電流ベクトル、iQ — 横軸電流ベクトル

[-200, 0, 200] [A] (既定値)

横軸電流ベクトル、iQ。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に、[モデル化の忠実度] を [表形式の Ld、Lq、および PM] に設定します。

Ld 行列、Ld(id,iq) — Ld 行列

0.0002 * ones(3, 3) [H] (既定値)

Ld 行列。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に、[モデル化の忠実度] を [表形式の Ld、Lq、および PM] に設定します。

Lq 行列、Lq(id,iq) — Lq 行列

0.0002 * ones(3, 3) [H] (既定値)

Lq 行列。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に、[モデル化の忠実度] を [表形式の Ld、Lq、および PM] に設定します。

永久磁石の鎖交磁束、PM(id,iq) — 永久磁石の鎖交磁束

0.1 * ones(3, 3) [Wb] (既定値)

永久磁石の鎖交磁束。

依存関係

このパラメーターを有効にするには、次のように設定します。

• [固定子のパラメーター化] を [Ld、Lq、L0 を指定]

• [モデル化の忠実度] を [表形式の Ld、Lq、および PM]

• [永久磁石の鎖交磁束のパラメーター化] を [鎖交磁束を指定]

トルク定数行列、kt(id,iq) — 力の定数行列

0.18 * ones(3, 3) [N*m/A] (既定値)

トルク定数行列。

依存関係

このパラメーターを有効にするには、次のように設定します。

• [固定子のパラメーター化] を [Ld、Lq、L0 を指定]

• [モデル化の忠実度] を [表形式の Ld、Lq、および PM]

• [永久磁石の鎖交磁束のパラメーター化] を [トルク定数を指定]

逆起電力定数行列、ke(id,iq) — 永久磁石の鎖交磁束

0.18 * ones(3, 3) [V/(rad/s)] (既定値)

逆起電力定数行列。

依存関係

このパラメーターを有効にするには、次のように設定します。

• [固定子のパラメーター化] を [Ld、Lq、L0 を指定]

• [モデル化の忠実度] を [表形式の Ld、Lq、および PM]

• [永久磁石の鎖交磁束のパラメーター化] を [逆起電力定数を指定]

固定子の零相インダクタンス、L0 — 固定子の零相インダクタンス

0.00016 [H] (既定値)

零相インダクタンス。

依存関係

このパラメーターを有効にするには、次のどちらかを行います。

• [結線種別] を [Y 結線] に、[零相] を [含める] に、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に設定します。

• [結線種別] を [デルタ結線] に、[固定子のパラメーター化] を [Ld、Lq、L0 を指定] に設定します。

固定子の相あたりの自己インダクタンス、Ls — 固定子の相あたりの自己インダクタンス

0.0002 [H] (既定値)

3 本の各固定子巻線の平均自己インダクタンス。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ls、Lm、Ms を指定] に設定します。

固定子のインダクタンス変動、Lm — 固定子のインダクタンス変動

-0.0002 [H] (既定値)

回転子の角度に伴う固定子巻線の自己インダクタンスと相互インダクタンスの変動量。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ls、Lm、Ms を指定] に設定します。

固定子の相互インダクタンス、Ms — 固定子の相互インダクタンス

0.00002 [H] (既定値)

固定子巻線間の平均相互インダクタンス。

依存関係

このパラメーターを有効にするには、[固定子のパラメーター化] を [Ls、Lm、Ms を指定] に設定します。

固定子の相あたりの抵抗、Rs — 固定子の相あたりの抵抗

0.013 [Ohm] (既定値)

各固定子巻線の抵抗。

零相 — 零相オプション

含める (既定値) | 除外

零相項を含めるか除外するかのオプション。

• 含める — 零相項を含めます。モデルの忠実度を優先するには、この既定の設定を使用します。このオプションを使用すると次のようになります。

  • 分割ソルバーを使用するシミュレーションでエラーが発生します。詳細については、分割ソルバーを使用したシミュレーションの高速化を参照してください。

  • [固定子の零相インダクタンス、L0] パラメーターが表示されます。

• 除外 — 零相項を除外します。デスクトップ シミュレーションのシミュレーション速度またはリアルタイムでの展開を優先するには、このオプションを選択します。

依存関係

このパラメーターを有効にするには、[結線種別] を [Y 巻線] に設定します。

回転子の角度の定義 — 回転子の角度測定の基準点

A 相の磁気軸と d 軸の間の角度 (既定値) | A 相の磁気軸と q 軸の間の角度

回転子の角度測定の基準点。モーターの構造セクションの図は、既定値の [A 相の磁気軸と d 軸の間の角度] を示しています。この値を選択すると、回転子の角度が 0 の場合に回転子と a 相の磁束が揃います。

[A 相の磁気軸と q 軸の間の角度] を選択すると、回転子の角度が 0 の場合に a 相電流によって最大トルクが生成されます。

鉄損

モデル — 鉄損の計算の有効化

なし (既定値) | 経験

鉄損の計算モデルを指定します。

開路鉄損、[P_hysteresis P_eddy P_excess] — 開路鉄損

[0, 0, 0] [W] (既定値)

[損失を求める電気周波数] で指定された周波数におけるヒステリシス損失、渦損失、および過剰損失に起因する開路鉄損の長さ 3 の行ベクトル。

依存関係

このパラメーターを有効にするには、[モデル] を [経験] に設定します。

短絡鉄損、[P_hysteresis P_eddy P_excess] — 短絡鉄損

[0, 0, 0] [W] (既定値)

[損失を求める電気周波数] で指定された周波数におけるヒステリシス損失、渦損失、および過剰損失に起因する短絡鉄損の長さ 3 の行ベクトル。

依存関係

このパラメーターを有効にするには、[モデル] を [経験] に設定します。

損失を求める電気周波数 — 損失を求める電気周波数

60 Hz (既定値)

ブロックで開路鉄損および短絡鉄損を測定する電気周波数。

依存関係

このパラメーターを有効にするには、[モデル] を [経験] に設定します。

短絡鉄損用の短絡実効値電流 — 短絡鉄損用の短絡実効値電流

95 [A] (既定値)

短絡損失の測定時に結果として得られた短絡実効値相電流。

依存関係

このパラメーターを有効にするには、[モデル] を [経験] に設定します。

機械

回転子の慣性 — 回転子の慣性

0.01 [kg*m^2] (既定値) | 非負のスカラー

機械並進端子 R に接続された回転子の慣性。値は 0 にできます。

回転子の減衰 — 回転子の減衰

0 [N*m/(rad/s)] (既定値) | 非負のスカラー

回転の減衰。

温度依存性

測定温度 — ブロックでモーター パラメーターを引用する温度

298.15 [K] (既定値)

ブロックでモーター パラメーターを引用する温度。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

抵抗温度係数 — 抵抗温度係数

3.93e-3 [1/K] (既定値)

抵抗を温度に関連付ける方程式の係数 α。詳細については、アクチュエータ ブロックの熱モデルを参照してください。既定値は銅に対応します。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

永久磁石の磁束温度係数 — 永久磁石の磁束密度が温度によって変化する非整数レート。

-0.001 [1/K] (既定値) | スカラー

永久磁石の磁束密度が温度によって変化する非整数レート。このパラメーターを使用すると、温度の上昇に伴ってトルクと誘起逆起電力が線形に減少します。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

熱端子

各固定子巻線の熱質量 — 各固定子巻線の熱質量

100 [J/K] (既定値)

A、B、および C の各巻線の熱質量値。熱質量は、温度を 1 度上げるのに必要なエネルギーです。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

回転子の熱質量 — 回転子の熱質量

200 [J/K] (既定値)

回転子の熱質量 (つまり、回転子の温度を 1 度上げるのに必要なエネルギー)。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定します。

回転子に関連する主磁束路の鉄損の割合 — 回転子に関連する主磁束路の鉄損の割合

90 (既定値)

回転子を通る磁路に関連する主磁束路の鉄損の割合。これにより、回転子の熱端子 HR と 3 本の巻線の熱端子 HA、HB、および HC に起因する鉄損の発熱量が決まります。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定し、[鉄損] タブで [モデル] を [経験] に設定します。

回転子に関連するクロス歯磁束路の鉄損の割合 — 回転子に関連するクロス歯磁束路の鉄損の割合

30 (既定値)

回転子を通る磁路に関連するクロス歯磁束路の鉄損の割合。これにより、回転子の熱端子 HR と 3 本の巻線の熱端子 HA、HB、および HC に起因する鉄損の発熱量が決まります。

依存関係

このパラメーターを有効にするには、[モデリング オプション] を [熱端子を表示] に設定し、[鉄損] タブで [モデル] を [経験] に設定します。

参照

[1] Kundur, P. Power System Stability and Control. New York, NY: McGraw Hill, 1993.

[2] Anderson, P. M. Analysis of Faulted Power Systems. Hoboken, NJ: Wiley-IEEE Press, 1995.

[3] Mellor, P.H., R. Wrobel, and D. Holliday. A computationally efficient iron loss model for brushless AC machines that caters for rated flux and field weakened operation. IEEE Electric Machines and Drives Conference. May 2009.

拡張機能

C/C++ コード生成
Simulink® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2013b で導入

R2024a: 固定子巻線の開放端構成

開放端構成内のマシンの固定子巻線をモデル化するには、[結線種別] パラメーターを [開放端] に設定します。次に、対応する電気量保存端子を有効にすると、PMSM ブロックに巻線の各端が表示されます。

R2021b: 電気的接続端子の更新

R2021b 以降では、複合端子と展開端子を切り替えるには、[電気的接続] パラメーターを [複合三相端子] と [展開三相端子] のいずれかに設定します。

このように変更されたため、以前のリリースで保存されたモデル内で、このブロックの [電気的接続] パラメーターを確認してください。

参考

Simscape ブロック

• BLDC | FEM-Parameterized PMSM | FEM-Parameterized Synchronous Machine | Hybrid Excitation PMSM | Magnetic Rotor | Motor & Drive (System Level) | PMSM (DQ0) | Rotating Air Gap

ブロック

• BLDC Commutation Logic | BLDC Current Controller with PWM Generation | BLDC Current Controller

トピック

• 事前にパラメーター化されたコンポーネントのリスト
• Choose Blocks to Model Motors or Actuators
• ブロックでの三相端子の展開と折りたたみ