Main Content

このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

永久磁石同期電動機のパラメーター化

スクリプトを開く

この例では、鎖交磁束が未知であるブラックボックスの永久磁石同期電動機 (PMSM) の逆起電力定数とトルク定数を推定する方法を説明します。逆起電力定数またはトルク定数のどちらかを使用して鎖交磁束を記述し、Simscape™ Electrical™ の PMSM ブロックをパラメーター化することができます。このパラメーター化によって、ブラックボックスであるモーターの動作をシミュレーションで正確に再現することができます。

この例では、シミュレーションの PMSM とブラックボックスの PMSM における極対数、固定子抵抗、および固定子インダクタンスが一致するように既に指定されています。

モデルを開く

モデルを開きます。

model='ee_pmsm_parameterization';
open_system(model)
set_param(find_system('ee_pmsm_parameterization','FindAll', 'on','type','annotation','Tag','ModelFeatures'),'Interpreter','off')

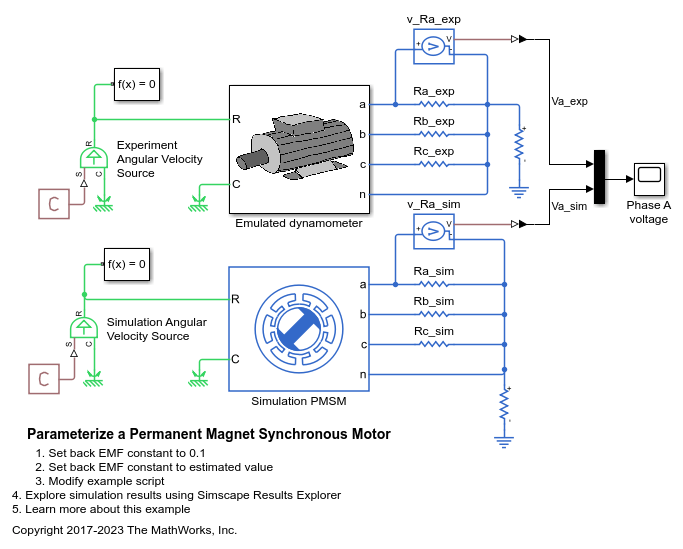
逆起電力定数の設定

シミュレーション PMSM の逆起電力パラメーター化オプションを選択し、その値を任意の既定値 0.1 V*s/rad に初期化します。

Simulation_PMSM = [model,'/Simulation PMSM'];
Ke = 0.1;
set_param(Simulation_PMSM,'pmflux_param','3');

あるいは、逆起電力パラメーター化オプションを設定し、[永久磁石の鎖交磁束のパラメーター化] の [Specify back EMF] を選択して [逆起電力定数] を指定することによって、その値を PMSM ブロック マスクから指定できます。

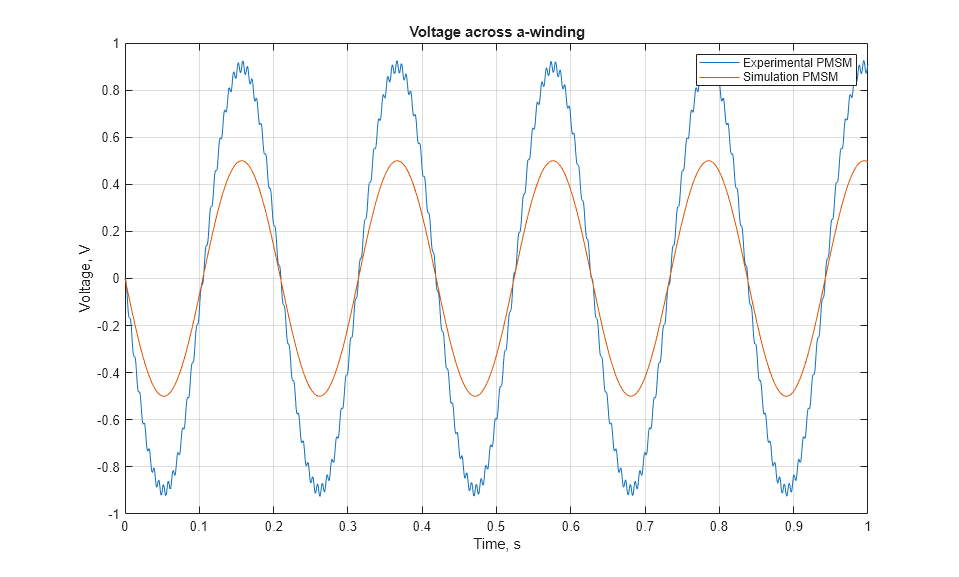
結果の比較

モデルをシミュレートし、実験 PMSM とシミュレーション PMSM の両方について、a 巻線にかかる電圧を経時的にプロットします。実験 PMSM とシミュレーション PMSM の間で電圧の振幅に有意差があることを確認します。

sim(model);
v_a_exp = simlog_ee_pmsm_parameterization.v_Ra_exp.V;
v_a_sim = simlog_ee_pmsm_parameterization.v_Ra_sim.V;
simscape.logging.plot({v_a_exp,v_a_sim},...
    'names',{'Experimental PMSM','Simulation PMSM'});
title('Voltage across a-winding')
ylabel('Voltage, V');

電圧定数の計算

次の定義式を使用して、ブラックボックスである実験 PMSM の電圧定数 $K_e$ を計算します。

$K_e=\frac{V_{a,pk}}{\omega}$,

ここで、$\omega$ は PMSM のシャフトの角速度で、$V_{a,pk}$ はモーターの a 巻線の電圧低下です。この方程式は、巻線を流れる電流が微小である場合にのみ有効です。この微小電流の制限は、極めて大きな抵抗を介して各巻線自由端を接地し、各巻線を実質的に開回路にすることによってモデル内で実効性をもちます。

$V_{a,pk}$ は、a 巻線の電圧低下の最大値と最小値の平均を取り、その結果を 2 で除算することによって計算されます。測定された電圧信号から最初に高周波ノイズをフィルターで取り除くことで、この計算の精度を向上させることができます。

window_size = 100;
v_a_exp_filt = filter(1/window_size*ones(1,window_size),1,v_a_exp.series.values);
v_a_exp_peak = (max(v_a_exp_filt)-min(v_a_exp_filt))/2;

角速度は、ソース ブロックから直接に測定できます。

angular_velocity_exp = mean(simlog_ee_pmsm_parameterization.Experiment_Angular_Velocity_Source.w.series.values);

これで、逆起電力定数を上記の結果から計算できます。

Ke = v_a_exp_peak / angular_velocity_exp;
disp(Ke);

    0.1803

逆起電力定数の変更

シミュレーション モーターの逆起電力定数を、前の節で計算した推定値 $K_e$ に変更します。

Simulation_PMSM = [model,'/Simulation PMSM'];
set_param(Simulation_PMSM,'pmflux_param','3');

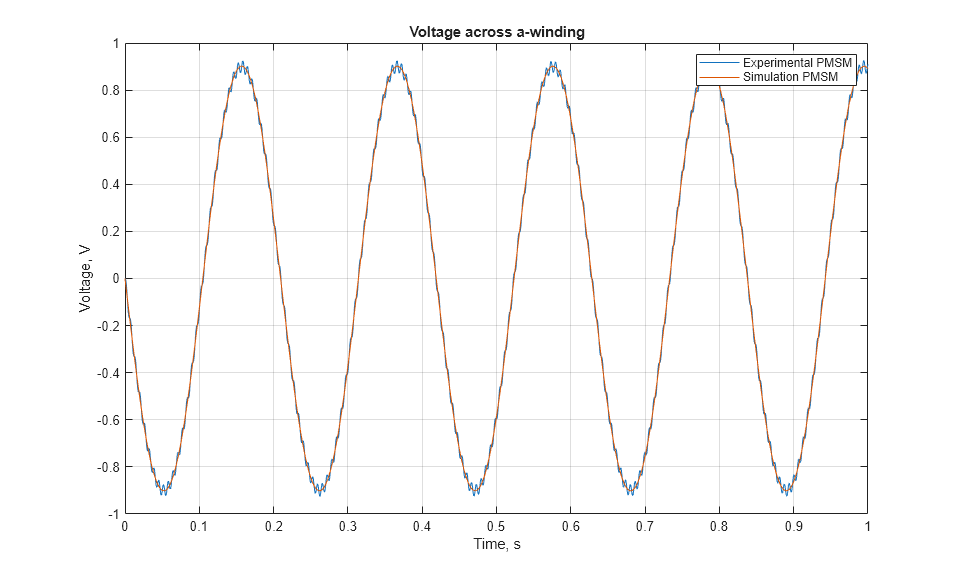
新しい結果の比較

モデルを再度シミュレートし、a 巻線にかかる電圧をプロットします。新たにパラメーター化された電圧定数によって、実験 PMSM の挙動を再現するシミュレーション PMSM の能力が向上します。

sim(model);
v_a_exp = simlog_ee_pmsm_parameterization.v_Ra_exp.V;
v_a_sim = simlog_ee_pmsm_parameterization.v_Ra_sim.V;
simscape.logging.plot({v_a_exp,v_a_sim},...
    'names',{'Experimental PMSM','Simulation PMSM'});
title('Voltage across a-winding')
ylabel('Voltage, V');

トルク定数の計算

次の定義式を使用して、ブラックボックスである PMSM のトルク定数 $K_t$ を計算します。

$K_t = \frac{2}{3}\left(\frac{T}{I_{a,pk}}\right)$,

ここで、$I_{a,pk}$ は a 巻線を流れるピーク電流で、$T$ は PMSM を駆動する総合的な機械トルクです。

i_a_exp = simlog_ee_pmsm_parameterization.Ra_exp.i;
i_a_sim = simlog_ee_pmsm_parameterization.Ra_sim.i;

T = abs(mean(simlog_ee_pmsm_parameterization.Experiment_Angular_Velocity_Source.t.series.values));

window_size = 100;
i_a_exp_filt = filter(1/window_size*ones(1,window_size),1,i_a_exp.series.values);
i_a_exp_peak = (max(i_a_exp_filt)-min(i_a_exp_filt))/2;

Kt = 2/3*T/i_a_exp_peak;
disp(Kt);

simscape.logging.plot({i_a_exp,i_a_sim},...
    'names',{'Experimental PMSM','Simulation PMSM'});
title('Current across a-winding')
ylabel('Current, A');

    0.1797

鎖交磁束のパラメーター化の比較

予想したように、測定されたトルク定数と逆起電力定数はほぼ同じ値 (0.18) をもち、モーターの極対数 $N$ を介して永久磁石の鎖交磁束 $\psi_m$ と関係しています。

$$K_e=K_t=N\psi_m .$$

モーターの永久磁石の鎖交磁束は、Simulation PMSM ブロック マスクの $K_e$、$K_t$、または $\psi_m$ のいずれかを指定することによってパラメーター化できます。モーターのデータシートでは、永久磁石の鎖交磁束よりも、逆起電力定数とトルク定数の方が記載されているのが一般的です。

詳細

詳細については、PMSMブロックのページを参照してください。